滚动轴承复合故障的混合协同诊断方法

黄大荣，陈长沙，赵 玲，孙国玺，柯兰艳

(1. 重庆交通大学信息科学与工程学院 重庆 南岸区 400074；2. 广东石油化工学院广东省石化装备故障诊断重点实验室 广东 茂名 525000)

滚动轴承作为旋转机械设备的基本元件，其损伤极大危害旋转机械设备整体运行的安全性，现有统计数据显示，旋转机械设备出现安全事故有30%是由滚动轴承故障引起的。因此，对滚动轴承故障诊断方法进行研究具有重要的现实意义[1-2]。

国内外学者从不同角度针对单故障振动信号进行了研究。文献[3]在综合考虑结构和运动参数的基础上，构建了三自由度滚动轴承故障振动信号模型，利用Runge-Kutta法求解其轴承非线性振动的频率及幅值，从而完成内圈故障的诊断。在此基础上，通过对滚珠与缺陷之间的接触过程进行分析，提出了包含转速参量的撞击力求解公式，利用Runge-Kutta法求解其非线性振动的频率及幅值，从而完成轴承内圈故障的诊断，取得较好的效果。文献[4]则以专家经验为主，在建立故障规则专家知识库的基础上，通过故障推理实现故障的判别诊断，由于充分考虑了行业专家的丰富经验，模拟效果较为显著。文献[5]则结合频谱自相关及经验模态分解构建了故障特征频率提取方法，在对经验模态分解各个分量进行贡献度比较的基础上，实现主要分量的频谱相关性分析判别，并用轴承的内外圈故障数据验证了算法的有效性。

上述算法主要是针对单故障进行判别分析，随着运行时间增加以及运行环境的改变，在旋转机械装备实际使用过程中，当滚动轴承出现故障，单故障模式很难凸显，往往是多种故障模式的混杂，以往的单故障诊断方法很难适应新模式下的故障诊断问题。因此，需要在单故障诊断算法的基础上，提出新的方法来进行复合故障的诊断及辨析。

为解决这个问题，文献[6]结合短时傅里叶变换和小波分析完成了耦合故障振动信号的特征提取，对热连轧机耦合振动信号机理进行了深入分析和研究，取得了较好的效果。文献[7]基于灰色理论构建了新的识别故障分量的故障诊断模型，并根据保护继电器(protection relays, PR)和断路器(circuit breaker, CB)的工作原理，实现了电源中断区域的识别和故障状态矢量的分配。文献[8]提出了一种改进的正交经验模态分解算法(orthogonal empirical mode decomposition, OEMD)，相比传统EMD算法，该方法能较好地消除噪声干扰，有助于提取故障特征，完成故障的分离和识别。文献[9]采用最小Shannon熵作为时间尺度分辨率的度量指标，对Morlet分析小波的参数优化进行选择，并利用奇异值分解技术对最优小波变化尺度进行迭代搜索，从而有效提高信噪比，完成复合故障的特征提取及识别。文献[10]针对铁路货车滚动轴承复合故障诊断问题，设计了基于陷波器的自适应复合故障诊断方法，陷波器可以实现故障的二次处理，对复合故障诊断有较好的准确率。文献[11]对液压泵振动信号进行经验模式分解，将分解出的模式分量函数进行包络谱分析，通过包络谱的能量分布特征进行故障类型判定。文献[12]利用最大相关峭度解卷积和重分配小波尺度熵方法完成旋转机械复合故障的诊断，该方法较好解决了由于旋转机械设备噪声引起的故障信号难以分离的问题。

上述复合故障诊断方法虽然在不同领域取得较好的效果，但本文在实际工作环境中发现滚动轴承故障诊断数据因受传输通道的影响，导致故障模式难以完全分离，故障诊断准确度也很难达到目标要求，故而需要根据实际工程数据，提出新的算法来克服这一问题[13-16]。

为此，本文在对二阶盲源分离理论及短时傅里叶变换进行基本介绍的基础上，基于二阶盲辨识和短时傅里叶变换构建新的滚动轴承复合故障诊断方法，并以广东省石化装备故障诊断重点实验室的轴承实测数据验证算法的有效性和合理性。

1 盲源分离理论介绍

二阶盲辨识是一种盲源分离方法，其分离盲信号思想为：首先假定观测信号X(t)不含噪声，盲源分离的线性瞬时混合过程可描述为：

在实际工程环境下，很难获取源信号矢量S(t)和混合系统的先验知识，需根据观测信号X(t)估计源信号值，假定为即：

式(2)可改写为：

式(3)表明，盲信号分离的目的是通过调节分离矩阵W，使分离出来的信号与源信号波形保持一致，即：

式中，D为非奇异对角矩阵，P为一置换矩阵。

根据式(3)和式(4)，得到：

则：

由上述推导，若W、A已知，可通过Y(t)估计出源信号S(t)。在实际操作中，源信号S(t)通过传输信道的过程中，会经过混合矩阵混合，只需要同时考虑到外部因素，加入一个误差矩阵V(t)，两者相加作为接收到的观测信号X(t)，通过相应盲源分离算法得到分离矩阵W，将X(t)与分离矩阵进行矩阵运算，就能得到源信号的估计信号矩阵Y(t)。综上，盲源分离的基本模型如图1所示。

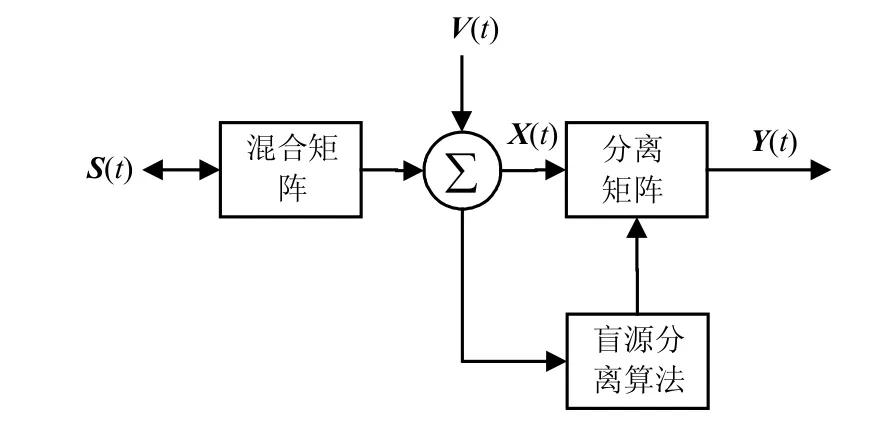
图1 盲源分离的基本思路

2 二阶盲辨识算法模型

基于上述盲源分离算法的基本介绍，利用二阶盲辨识进行复合故障信号盲源分析的主要思路如下：首先，对复合故障信号进行白化预处理，提高算法分离性；然后，采用联合对角化技术，基于二阶盲辨识(second-order blind identification, SOBI)方法，实现对复合故障信号的分离。

2.1 白化预处理

在二阶盲辨识进行盲源分离过程中，为了能够分离出源信号，常常希望混合信号中的各分量之间相互统计独立，对混合信号进行白化预处理的目的是去除信号各个分量的相关性，预白化处理的基本步骤如下：

2) 对Rx进行奇异值分解，即：

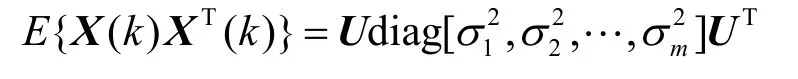
式中， U = [u1, u2,… ,um]的列是Rx的左奇异向量。根据 σ1≥ σ2≥ … ≥ σn＞ 0 ,σn+1= … = σm=0确立源信号的数目为n。

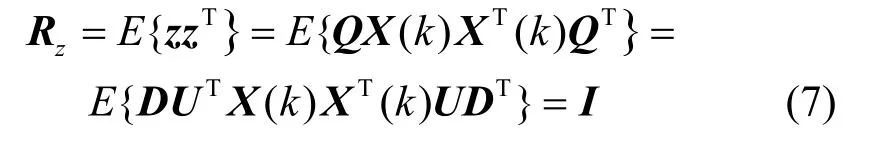
由上述过程可以看出，利用Q进行预白化处理使X(k)变为z(k)，可使其分量互不相关，达到解相关的目的。

2.2 联合对角化

上述分析表明，经过2.1节中白化预处理后，观测信号可修订为z(k)，白化矩阵为Q，白化后的信号协方差矩阵是单位矩阵，如式(7)所示。

理论上而言，联合对角化的实现是通过寻找正交矩阵V，实现对非零延迟相关矩阵组的联合对角化。即，寻求正交矩阵V，满足目标函数：

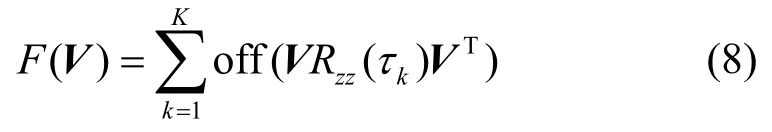
显然，通过正交矩阵V可得到y(k)，即：

由上述过程可以看出，通过白化后信号的相关矩阵进行对角化，利用对角化后的正交矩阵，就可得到源信号的估计值，完成对复合故障信号的分离。

3 短时傅里叶变换

理论分析结果表明，上述二阶盲源分离进行盲辨识得到信号具备无序性及相似性特点，因此将分离后的信号进行短时傅里叶变换，利用分离信号的短时傅里叶变换时频谱图与原信号时频谱图进行比较确认，完成复合故障的诊断。基本思想为：在信号傅里叶变换前乘上一个时间有限的窗函数，并假定非平稳信号在分析窗内的短时间隔内是平稳的，通过窗在时间轴上的移动使信号逐段进入被分析状态，得到一组局部的频谱，进一步根据不同时刻“局部”频谱的差异性，辨识信号的时频特性。基本定义如下：

定义 1 给定一个时间宽度很短的窗函数η( k )，让窗滑动，则信号z(k)的短时傅里叶变换定义为：

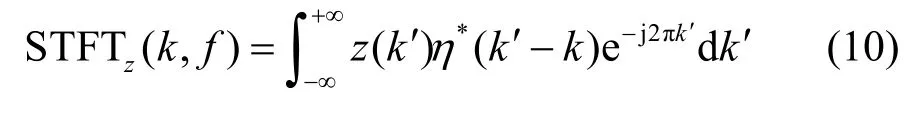
定义表明，对于给定时刻k，STFTz(k,f)即为该时刻对应的短时傅里叶频谱。由于窗函数η(k)的存在，短时傅里叶变换具有局域特性，它既是时间的函数，也是频率的函数，能较好地反映信号的变化特征，因此可以弥补二阶盲源辨识理论的不足。

4 二阶盲辨识协同短时傅里叶变换的复合故障诊断框架及算法

基于上述理论分析，设计二阶盲辨识协同短时傅里叶变换的滚动轴承复合故障诊断算法如下：

1) 观测信号预白化处理。计算观测信号的零延迟相关矩阵并进行奇异值分解，即Rx=并令Z(k) = QX(k)。

2) 联合对角化，得到分离信号。先计算白化后信号的非零延迟相关矩阵组 Rz(τ)={Rz( τ1),Rz( τ2) ,… ,Rz( τk)}。寻找正交阵V，使其满足： VTRz(τi)V =Mi，其中{ Mi} 是一组对角矩阵。

3) 计算分离信号 y ( k ) = VTQX ( k )。

4) 对分离信号进行短时傅里叶变换。将分离信号进行短时傅里叶变换，得到分离信号对应的时域图与频域图，通过对比源信号的时域图与频域图，根据趋势一致性辨别分离信号对应的故障类型，从而识别复合故障。其基本框架结构如图2所示。

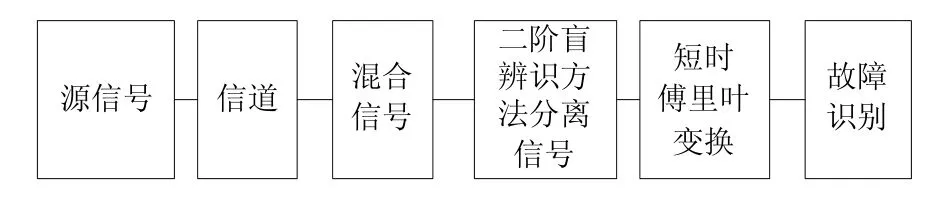
图2 基于二阶盲辨识和短时傅里叶变换的轴承复合故障诊断基本框架

5 实验验证

5.1 仿真实验

为验证本文算法的有效性，采用图3中信号作为源信号，分为信号1～4个信号源，并作为源信号通过信道传输，生成混合信号，如图4所示。

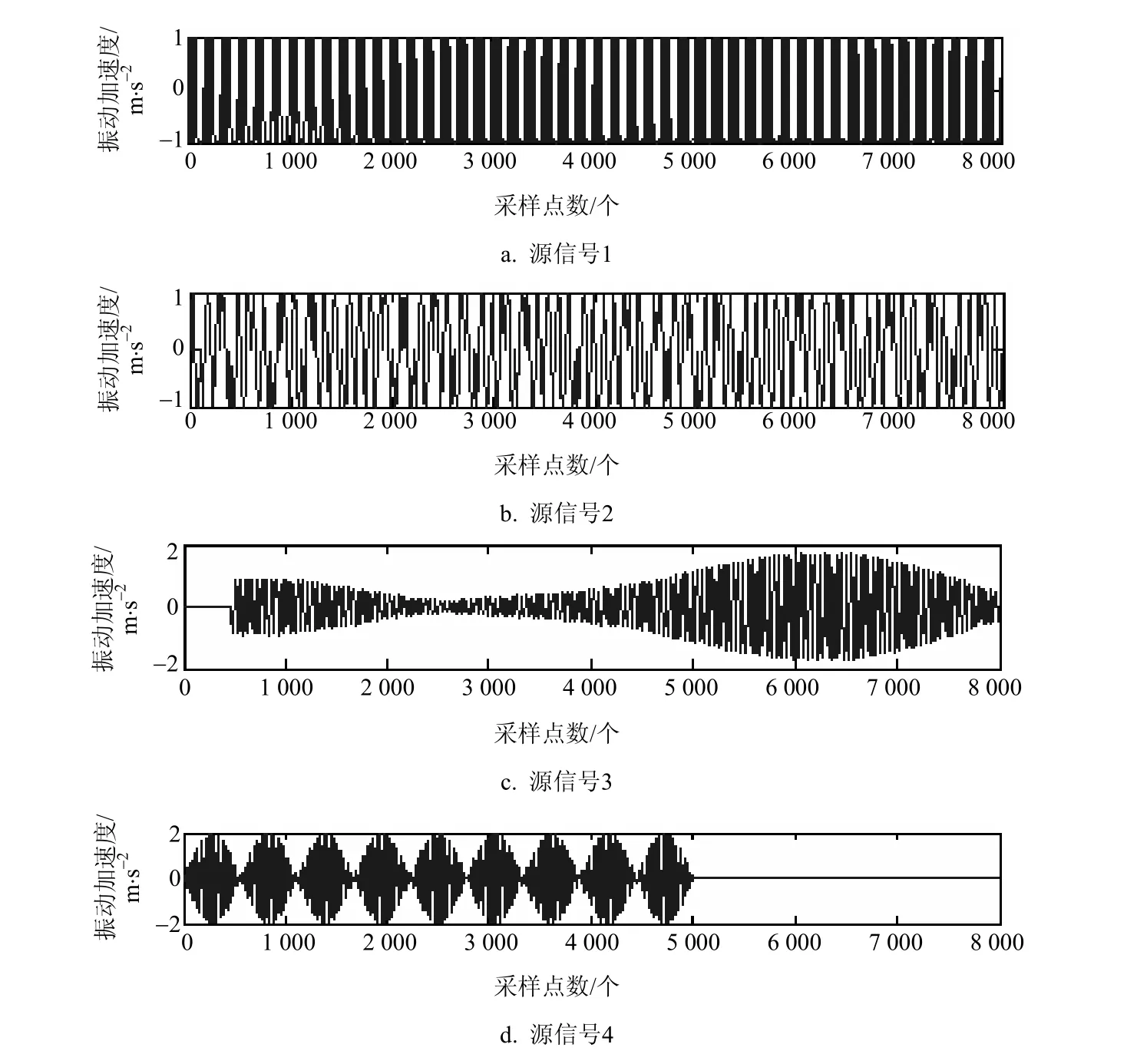
图3 源信号

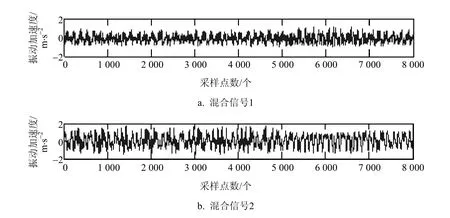
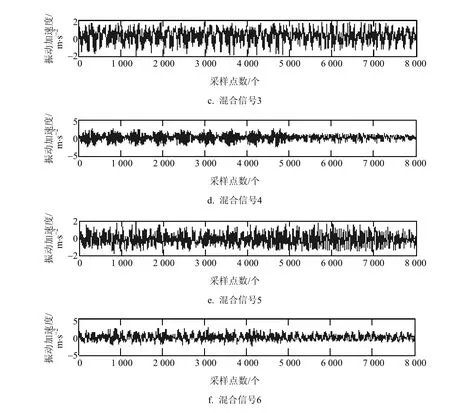
图4 混合信号

图4 中，源信号通过信道传输后，转换成包含6路信号的混合信号，分别利用二阶盲辨识方法和快速独立分量分析方法对混合信号进行分解，得到的效果图分别如图5、图6所示。

从图5中可以看出，二阶盲辨识能完全地分离出混合信号与图3中源信号的对应关系：分离信号1对应源信号1，分离信号2对应源信号2，分离信号3对应源信号4，分离信号4对应源信号3，另外分离信号4和5由系统传输信道的噪声引起，不包含源信号的信息。

图6中分离的信号与源信号的对应关系为：分离信号3对应源信号1，分离信号4对应源信号2，而分离信号1和2由于未能将源信号中的信号3和4分离，因此不能识别出对应的源信号。由此可以看出，快速独立分量分析只能分离部分信号。

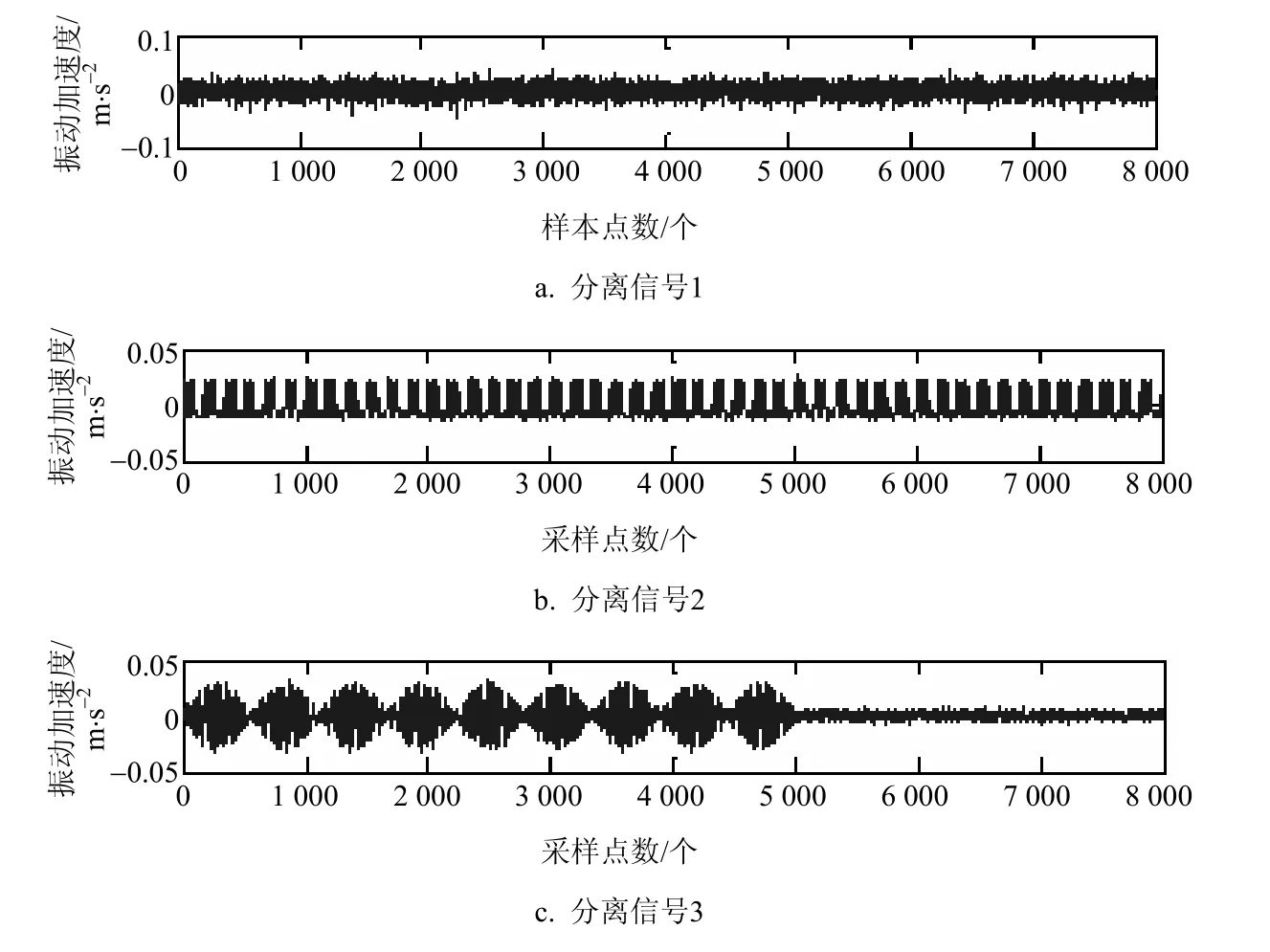
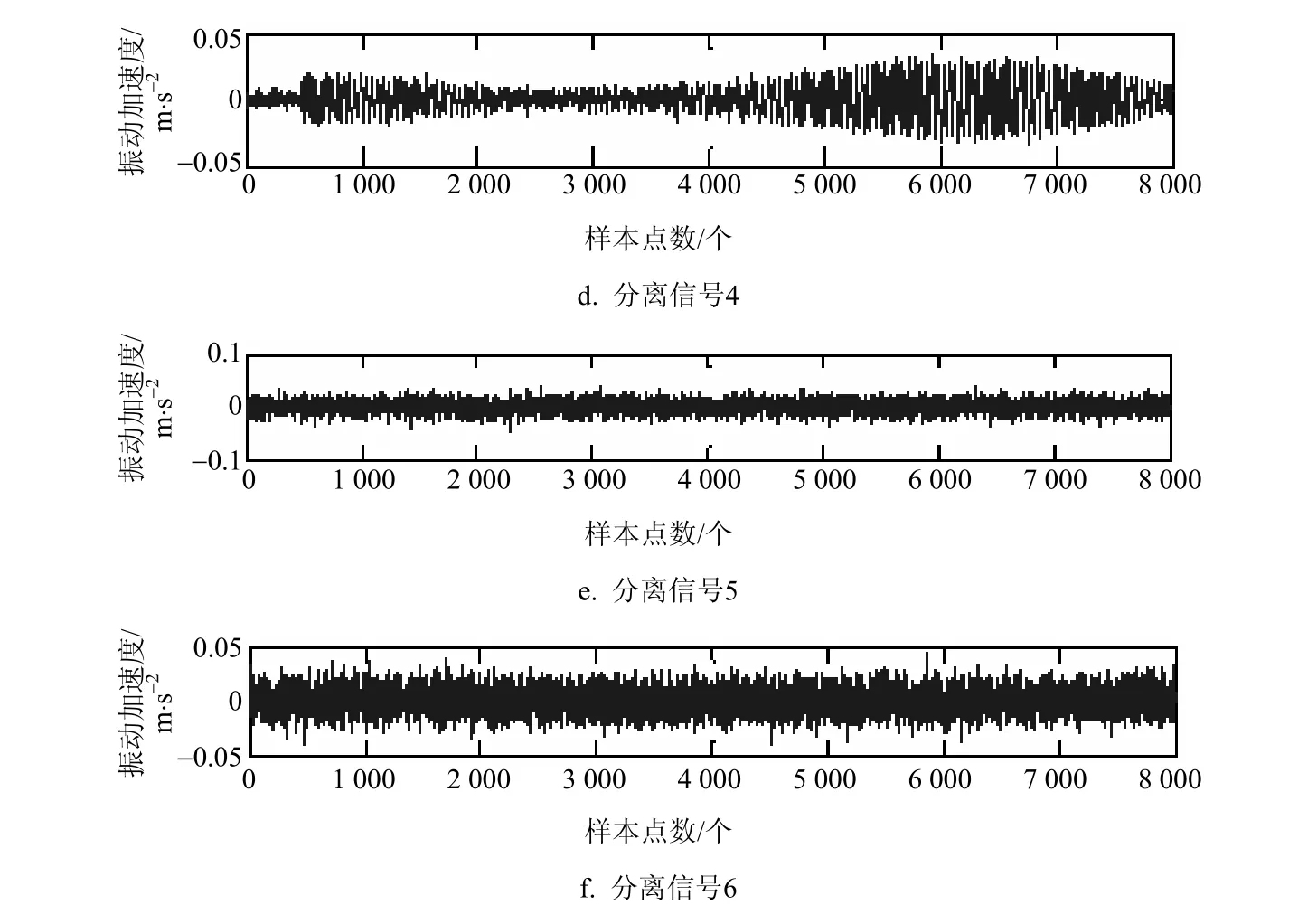
图5 二阶盲辨识分离后的信号

图6 快速独立分量分析分离信号

显然，相比快速独立分量分析分离方法，二阶盲辨识分离方法分离效果能更好满足实际环境的需求，这表明二阶盲源辨识分离方法符合实际需求。

5.2 实例验证

为进一步验证本文提出的模型和算法的有效性，将其应用到某型装备的轴承多重故障的实际诊断中。仿真实验依托于广东省石化装备故障诊断重点实验室平台，该平台以工业现场炼化装置大型旋转机械机组为参照，设计了一套单级离心风机故障诊断机组，该机组是工业机组典型结构，由电动机-变速箱-压缩机组成，支撑方式为悬臂式，负载是5.5 kW单级离心风机。该机组通过更换各类故障的齿轮、轴承、传动轴等部件，实现模拟悬臂式离心式压缩机或膨胀机机组常见的单一故障和复合故障。其中单级离心风机故障诊断机组如图7所示。

图7 单级离心风机故障诊断机组

图8 部分实验故障配件

针对复杂装备常见轴承故障，结合典型的工业机组结构和负载，在上述单级离心风机故障诊断基础上，设计了一套与系统匹配的故障配件，包括轴承外裂、轴承内裂、轴承滚珠磨损、轴承缺滚珠、裂齿、齿轮磨损等，部分实验故障配件如图8a～图8d所示。

基于以上故障配件，试验选择NSK NN3021轴承型号进行多重故障仿真，将振动加速度传感器垂直固定于轴承上方，采集无负载下轴承直径为7 mm，轴承内圈故障、滚珠故障、外圈故障(含3个位置)的12K驱动端加速度数据，其故障源信号如图9所示。

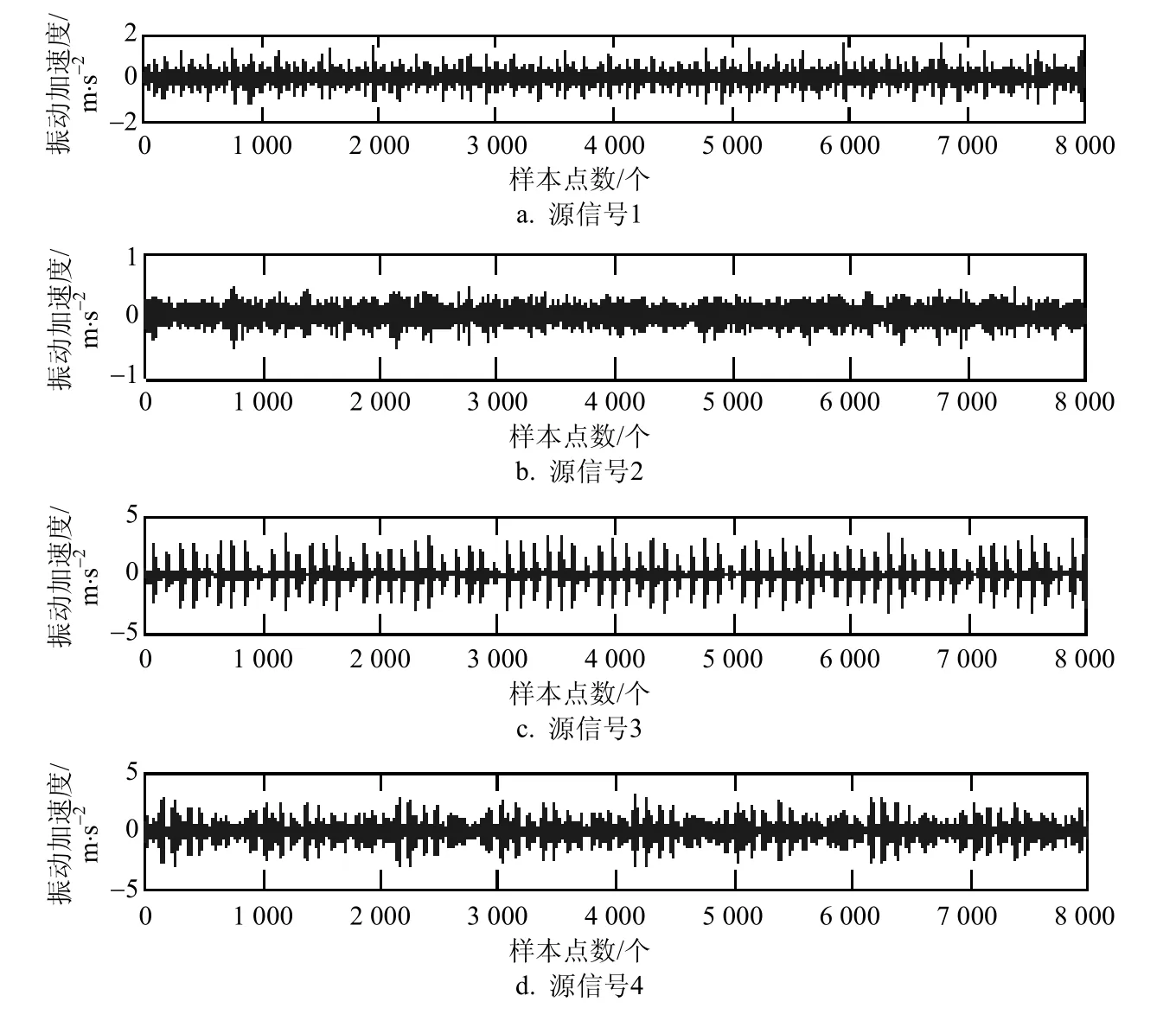
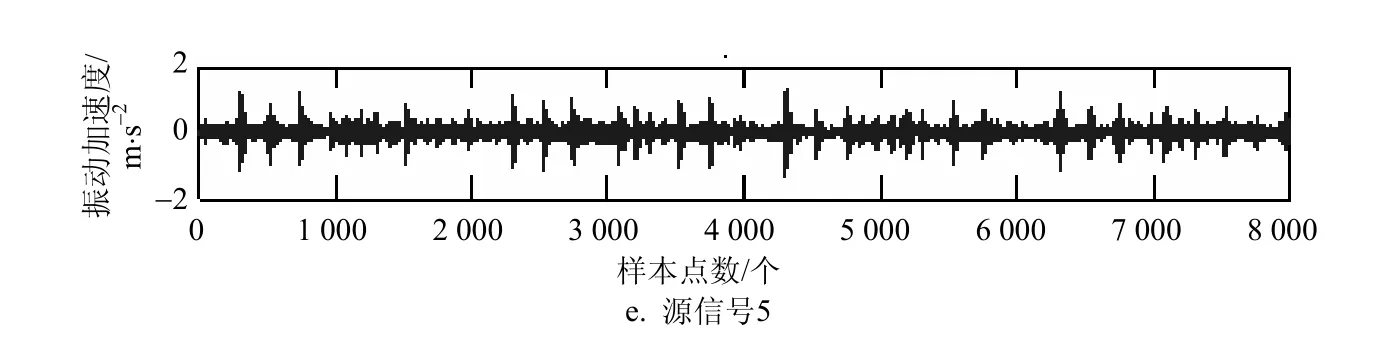
图9 滚动轴承故障源信号

图9 中，从上到下源信号1～5依次为滚动轴承内圈故障、滚珠故障、3个方向上的外圈故障(分别为3点钟、6点钟、12点钟方向)。

为获取复合故障数据，将源信号经过信道传输，混合信道特性获得复合故障信号，如图10所示。

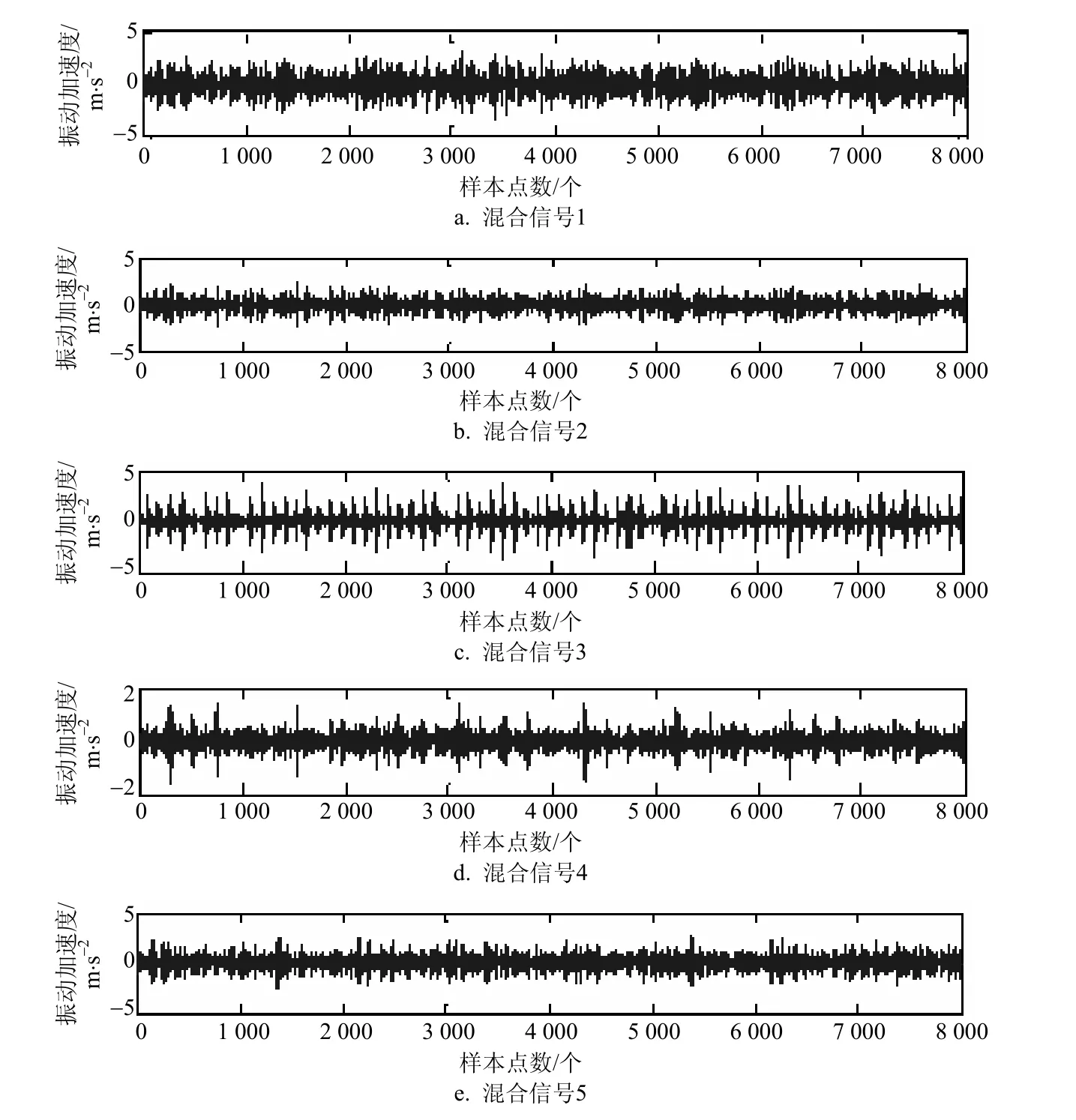
图10 混合信号

图10 中，源信号经过信道传输后，对应接收到的混合信号，由于混合了信道特性，使源信号的故障类型难以分辨，因此，需通过二阶盲辨识方法进行盲源信号的分离，分离效果如图11所示。

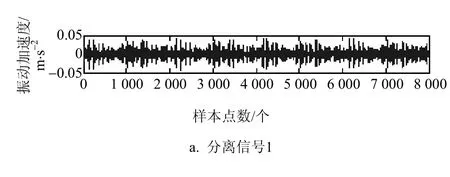
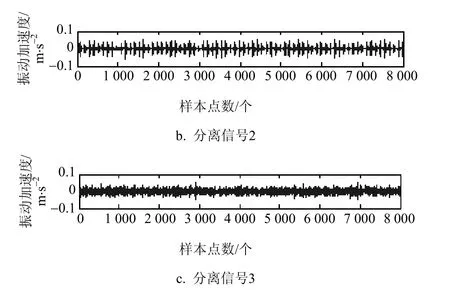
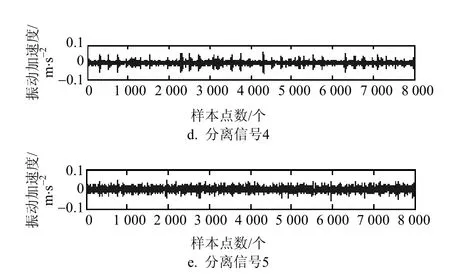
图11 二阶盲辨识法分离出的信号

从图11中可以看出，利用二阶盲辨识法得到的分离信号编号分别为：1～5；通过分离信号图对比源信号图7，可以发现，分离得到的信号顺序与源信号不一样，并且很难直接确认分离出来的信号对应的故障类型。因此，可在此基础上，采用短时傅里叶变换方法，将分离出来的信号进行短时傅里叶变换，将其时域与频域图与源信号时域、频域图对比，并根据一致性确认所对应的信号。为了进一步验证该方法的有效性，采用了经二阶盲辨识得到的图11中的分离信号2和分离信号5分别进行短时傅里叶变换，并将源信号中对应的源信号时域、频域图进行对比，其实验结果分别如图12和图13所示。

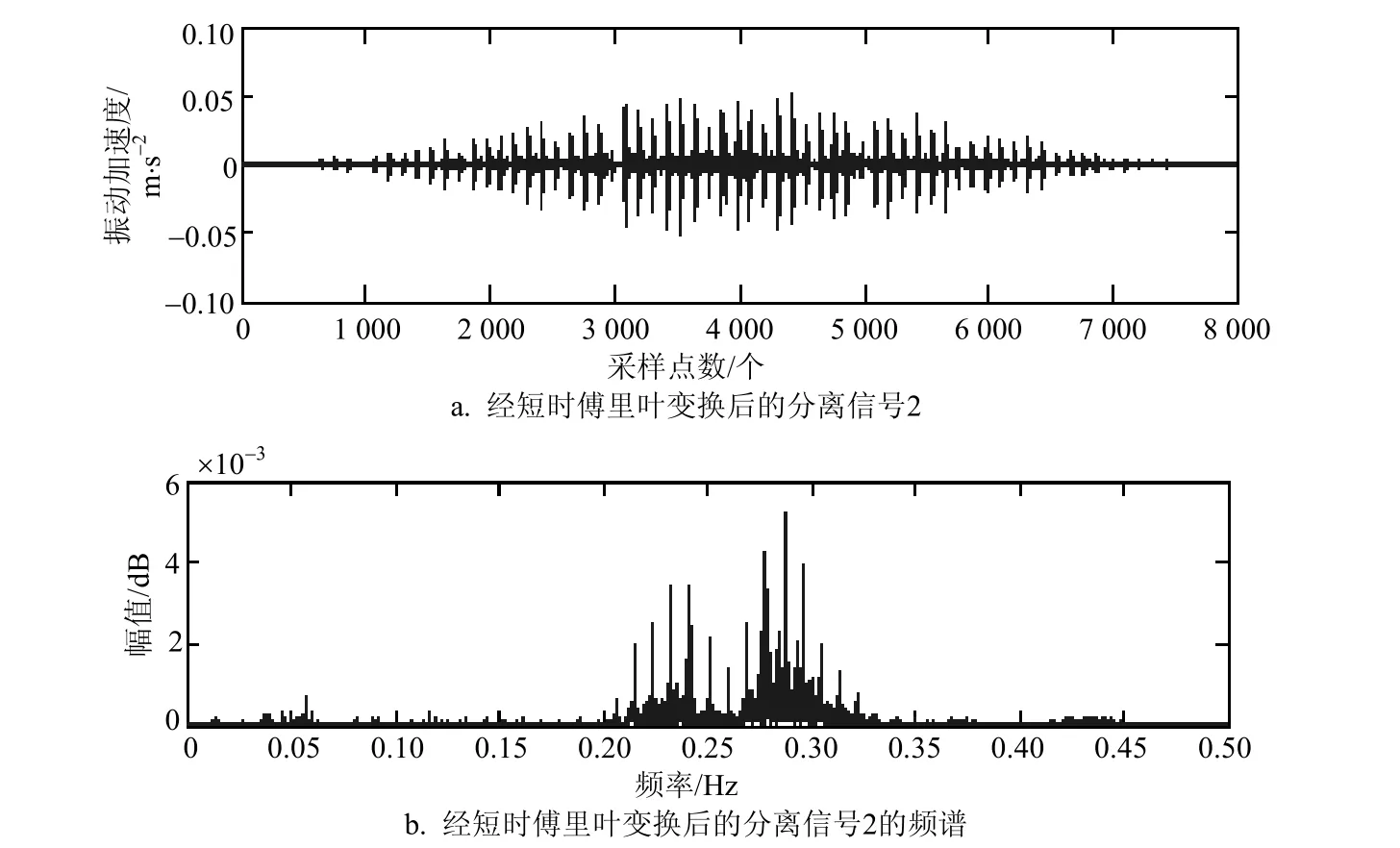
图12 分离信号2进行短时傅里叶变换后的时频图

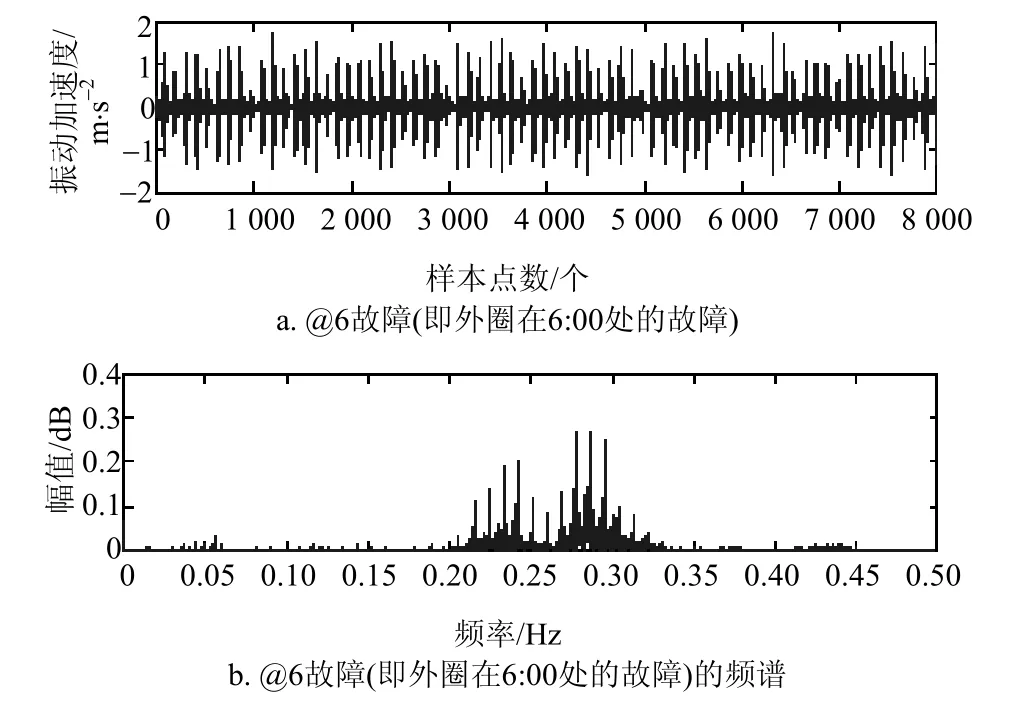
图13 外圈6点钟方向上的故障对应的时频图

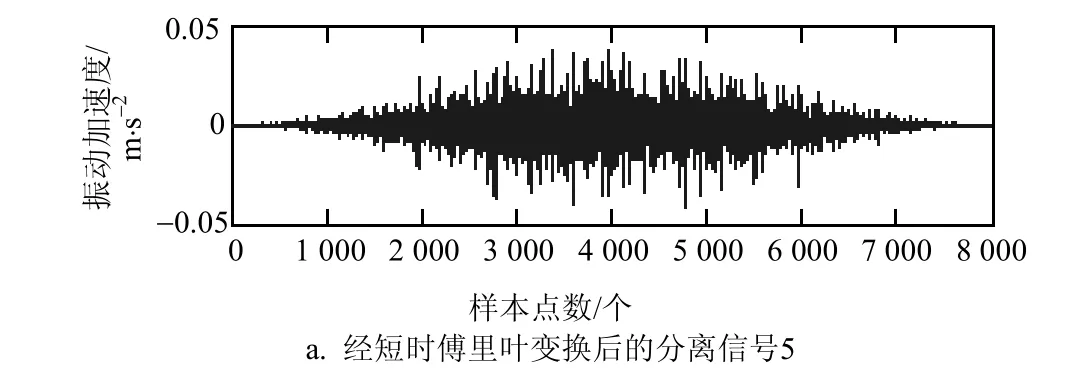
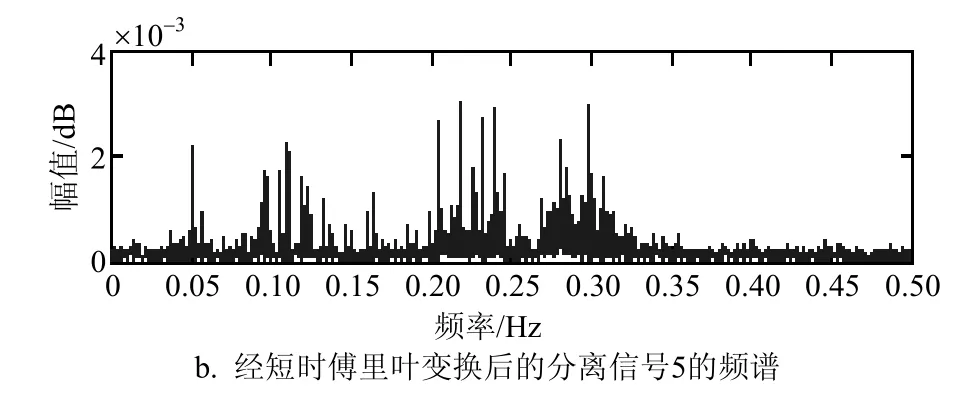
图14 分离信号5进行短时傅里叶变换后的时频图

对比图12和图13可以看出，分离出的信号2进行短时傅里叶变换的时域图为局部的，对比效果更准确，两者的时域图趋势基本一致。进一步再对比频域图，可以看出，频域图趋势也基本一致。因此可以确认，分离信号2对应的故障类型为外圈6点钟方向上的故障；同理，对分离信号5进行短时傅里叶变换，如图14所示。

类似地，对比图14和图15可以看出，分离信号5进行短时傅里叶变换的时域图与源信号时域图趋势基本一致。进一步再对比频域图，可以看出，频域图趋势基本一致，显然，分离信号5对应的故障类型为内圈故障；同理，可以确定分离出的信号1对应的故障类型为外圈3点钟方向上的故障，分离出的信号3对应的故障类型为滚珠故障，分离出的信号4对应的故障类型为外圈12点中方向上的故障。

实验结果表明，本文提出的方法能很好地完成滚动轴承复合故障诊断的辨识及诊断。

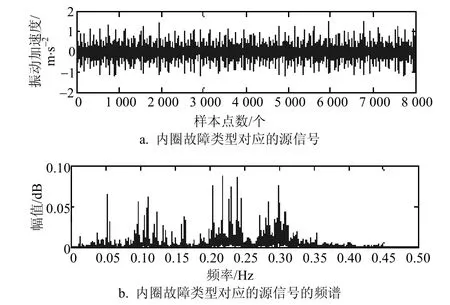
图15 内圈故障对应的时频图

6 结 束 语

本文针对传统复合故障诊断方法存在故障难以完全分离的缺点，提出了基于二阶盲辨识协同短时傅里叶变换的滚动轴承复合故障诊断新方法。并在模拟验证二阶盲源辨识方法有效性的基础上，以广东省石化装备故障诊断重点实验室的实验平台数据进行了算法有效性的验证。实验结果表明，本文提出的算法能较为有效的辨识复合故障模式。

但遗憾的是，由于在实际工业环境中，大型机组设备存在强噪声背景，会影响故障数据分离的准确性，如何改进算法对背景噪声进行处理，是需要进一步解决的工作，限于篇幅，将另作详细介绍。

本文的研究工作得到了重庆交通大学研究生教育创新基金(2017S0105)的资助，在此表示感谢！