反应位移法在地下综合管廊抗震设计中的应用

施有志, 华建兵, 李秀芳, 林树枝

1.厦门理工学院土木工程与建筑学院，福建 厦门 3610212.上海交通大学船舶海洋与建筑工程学院，上海 2002403.合肥学院建筑工程系，合肥 2300134.厦门市建设局，福建 厦门 361003

0 引言

地下综合管廊是将两种以上的城市管线集中设置于同一人工空间中所形成的一种现代化、集约化的城市基础设施。综合管廊是重要的生命线工程，设计时应考虑到地震作用影响，但现有综合管廊规范[1]仅要求按乙类建筑物进行抗震设计，并未给出详细的计算方法。已有震害调查、理论分析及试验研究表明，地下结构在地震作用下随周围土体一起运动，其加速度、位移等结构反应与周围土体基本一致[2]。基于地下结构地震响应的特点，日本学者于20世纪70年代提出反应位移法，并成功用于抗震设计[3]。该方法提出后，受到了国内外学者的高度重视，在理论与计算方面不断改进，并在实践中得到了应用。刘晶波等[4-6]提出了反应位移法的改进方法，即利用土-结构相互作用模型直接反映土体与结构间的相互作用；宾佳等[7]对6种静力有限元求解弹簧系数的方法进行对比分析计算，得出各弹簧系数求解方法的适用性；安军海等[8]探讨了影响反应位移法计算精度的几个主要因素，包括不同规范推荐的土体相对位移及剪应力的计算公式、土弹簧刚度的确定方法、分层土体与等效单层土体的差异、荷载-结构模型的选择等；崔杰等[9]介绍了8种不同关键问题组合方式的反应位移法，并采用这8种不同组合方式分析了典型矩形横截面隧道在基岩垂直入射剪切地震波作用下的内力，并将计算结果与动力有限元法结果进行了对比；王国波等[10]对反应位移法中土弹簧刚度的不同确定方法、分层土体与等效单层土体的位移模式、线性与非线性时土体位移模式等进行了研究。

目前，反应位移法已成为抗震设计中的主要方法之一，被编入设计规范[11-12]。然而，位移反应法在抗震设计分析时仍存在较大的误差。究其原因，主要是规范给出的反应位移法计算模型、基床系数等关键问题尚不够明确；此外，该方法也有明确的适用条件要求，其只适合于均匀土层，结构横截面没有剧变的情况。对于软硬相间地层、结构断面变化剧烈的条件并不适用[13]。目前对反应位移法在综合管廊抗震设计方面应用的报道仍较少[14]。

综上所述，反应位移法虽然相对简单却也存在诸多问题。在国家大力投入建设综合管廊的背景下，有必要完善综合管廊的抗震设计方法，确保重大生命线工程具有良好的抗震性能。本文以厦门地区复合地层中的双仓预制拼装混凝土管廊结构为对象，采用反应位移法对综合管廊结构进行地震反应计算分析，详述其具体应用技术细节，补充规范中未明确的应用要点及参数确定方法，借助SAP2000结构分析软件进行最终的结构受力计算，并与PLAXIS软件的动力时程分析法结果作对比，以期为规范方法的具体实施提出较为全面合理的技术建议。

1 计算原理及方法

反应位移法的主要思想是把地震荷载作用下的地层周围剪应力、结构自身惯性力等施加于结构，同时把地层在地震时产生的位移差(相对位移)通过地基弹簧以静载的形式作用于结构上，从而求得结构的应力和变形等。

1.1 地基弹簧刚度

在反应位移法计算模型中，以集中地基弹簧来反映一定面积的土层作用，需要将基床系数(即单位面积地基弹簧刚度)乘以作用面积，得到相应的地基弹簧刚度，即

k=Kld。

(1)

式中：k为压缩或剪切地基弹簧刚度(kN/m)；K为基床系数(kN/m3)；l为地基的集中弹簧间距(m)；d为土层沿隧道与地下车站纵向的计算长度，一般取单位长度(m)。

一般可采用如下方法确定基床系数。

1)我国经验公式[5]

Kn=3G；

(2)

Kt=βKn。

(3)

式中：Kn、Kt为分别为土层法向和切向的基床系数(kN/m3)；G为地震震动最大应变幅度相应的地基土剪切模量(kPa)；β为换算系数，其值可取为1/3。

2)日本经验公式[15]

顶板和底板的法向基床系数为

(4)

顶板和底板的切向基床系数为

(5)

侧墙的法向基床系数为

(6)

侧墙的切向基床系数为

(7)

式中：E0为地基土的动变形模量(kPa)；Bv为地下结构顶板和底板的宽度(m)；Bh为地下结构侧墙的高度。

3)静力有限元法

1.2 地层位移

对于刚度较均匀的成层分布地层，可采用假定地层变位法确定地震反应水平位移随深度的变化并计算土层相对位移。目前大多将地震时地层位移沿深度的变化假设为余弦函数，城轨抗震规范[16]中的附录E给出的计算公式为

(8)

式中：u(z)为深度z处自由土层的地震反应位移(m)；umax为场地地表最大水平位移(m)；z为地下结构面距地表的深度(m)；H为地震基准面距地表面的深度(m)。

土层相对位移计算公式为

u′(z)=u(z)-u(zB)。

(9)

式中：u′(z)为深度z处相对于结构底部的自由土层相对位移(m)；u(zB)为结构底部深度zB处的自由土层地震反应位移(m)。土层地震反应位移应取地下结构顶底板位置处自由土层发生最大相对位移时刻的土层位移分布。

需要注意的是，式(9)得出的是相对于结构底板位置处的位移，需要位移施加于结构两侧面压缩弹簧及上部剪切弹簧远离结构的端部。

作用在结构上的土层地震反应位移也可以转换为直接施加在结构上的等效荷载：

p(z)=k[u(z)-u(zB)]。

(10)

式中，p(z)为直接施加在结构上的等效荷载(kN)。

为了得到更加精确的土层位移，也可以采用Shake91等一维地震反应分析程序或者通用有限元程序进行一维土层地震反应分析，以获得相应计算参数。

1.3 地震剪应力

正式发布的城轨抗震规范中并未明确给出地震作用下土层对结构周围剪应力的计算公式，但北京城轨交通设计规范[18]及相关研究文献[19]中大多将地震时地震剪应力沿深度的变化假设为正弦函数，计算公式如下：

(11)

式中：τ(z)为深度z处单位面积作用的周边地层剪应力(kPa)；Gd为地层动剪切模量(kPa)。

矩形结构侧壁剪应力可假定为均匀分布[11]，按下式计算：

(12)

式中：τU、τB、τS分别为结构顶板、底板、侧墙处地层剪应力(kPa)。

2 建模及计算

2.1 计算思路及方案

首先，按照最简化的计算方法对土层进行均质等效化处理，通过等效剪切波速换算得到土层等效动变形模量，并基于此计算基床系数和地基弹簧刚度；按假定位移法计算土层相对位移，再按假定剪应力分布模式计算结构周围土层剪应力；根据结构埋深及场地条件估算水平地震系数，进而计算结构惯性力；借助结构有限元程序计算地震荷载作用下的管廊结构内力。

然后，分别按照日本公式法、城轨抗震规范静力有限元法、“李亮法”计算基床系数，对比分析基床系数不同计算方法对结构地震反应的影响。

最后，考虑土体分层特点，分层计算结构顶底板处地层剪应力，再分别按照日本公式法、城轨抗震规范静力有限元法、“李亮法”计算分层土体基床系数，研究分层计算地层剪应力对结构地震反应的影响，并与二维动力时程有限元计算结果进行对比分析。

计算流程如图 1所示。

为了考察各种基床系数、地层剪应力计算方法对结构地震反应的影响，考虑了8种计算方案，如表 1所示。

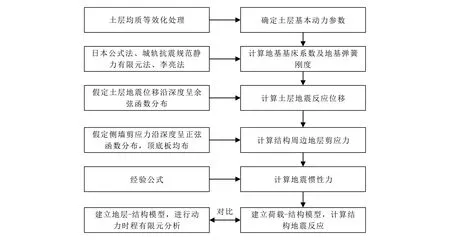
图1 计算流程图Fig.1 Calculation flow chart

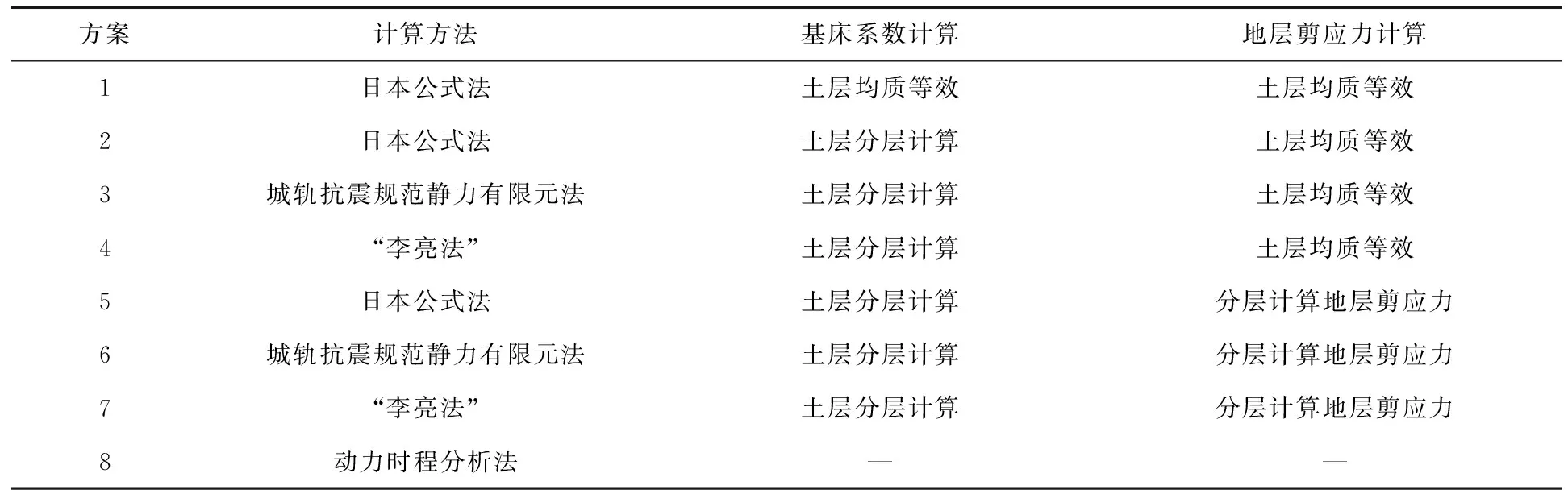
表1 综合管廊地震反应计算方案

2.2 管廊及地层基本参数

以预制拼装式双仓混凝土管廊为计算对象，其横截面5.6 m×2.8 m，壁厚0.3 m，顶板埋深2.0 m，底板埋深4.8 m。地层条件取厦门典型地层，自上至下依次为素填土(0～3.6 m)、粉质黏土(3.6～9.6 m)和残积砂质黏性土(9.6～30.0 m)。地震作用基准面取为与数值模型相同，即地表以下30.0 m处。在反应位移法计算中仅考虑水平地震作用。土体本构采用小应变硬化(HSS)模型，参数见表 2。

2.3 管廊结构反应位移法计算模型

借助SAP2000软件进行管廊结构地震反应位移法计算，建立双仓管廊结构的平面框架模型，如图 2所示。结构构件采用梁单元模拟(矩形截面，C30材料)，梁单元划分时均按每隔0.5 m划分一个单元。

地下结构地震反应分析中的难点之一是地层弹簧的实现。由于地层通常不会对结构产生拉力，因此地层弹簧单元的力学模型需要满足仅可受压不能受拉的特点。

ANSYS程序通常采用弹簧单元Combin14来模拟地层与结构之间相互作用的地层弹簧(该单元能够承受轴向的拉压)，采用梁单元Beam3模拟结构构件，在建好计算模型并设置好荷载及边界后，通过多次反复进行，直到计算结果中没有受拉的弹簧为止。这一过程需要通过反复计算、检查、调整模型，实现起来较为繁琐。

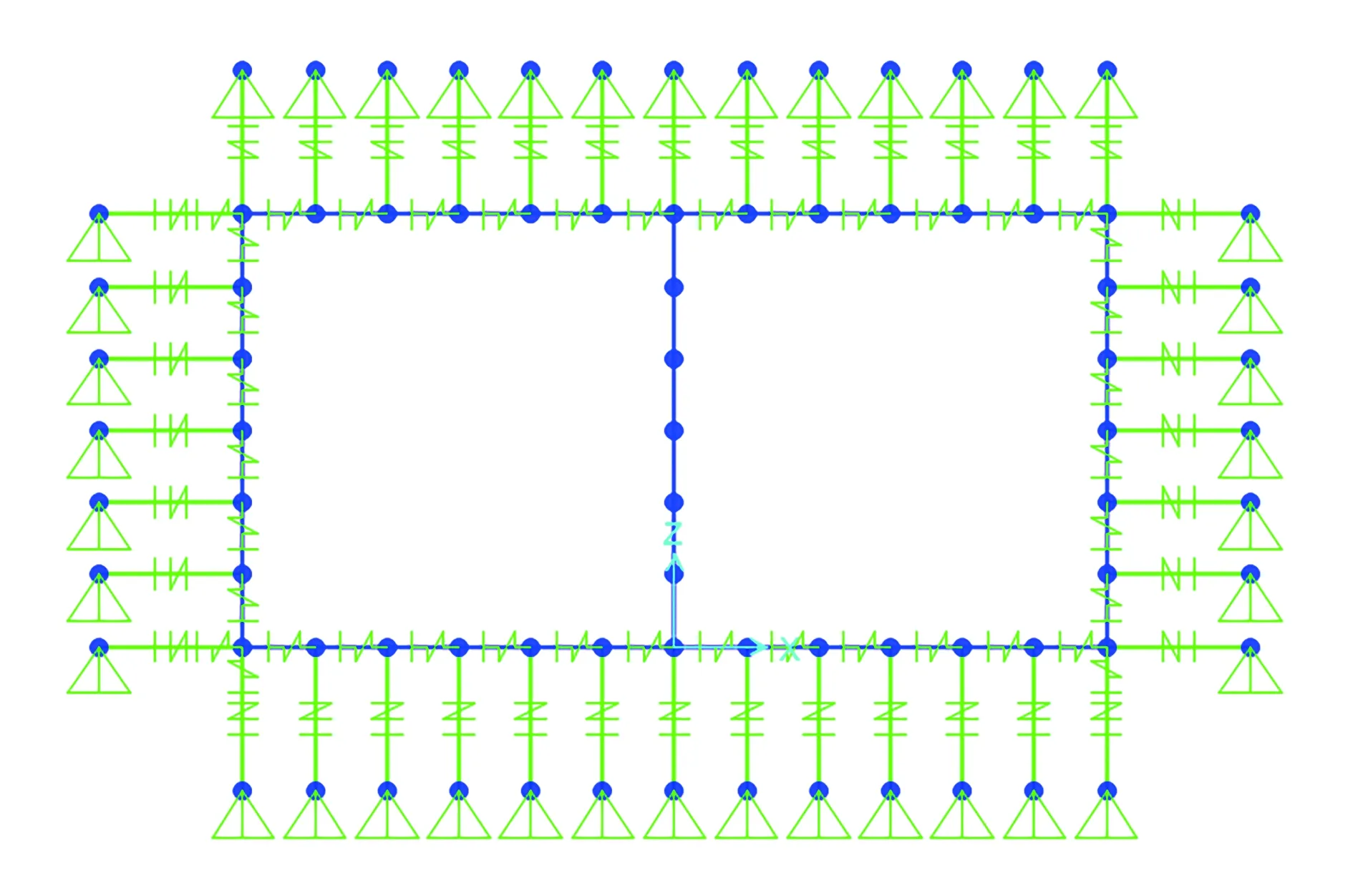
图2 双仓管廊结构反应位移法SAP2000结构模型网格图Fig.2 Double storehouse gallery structure response displacement method SAP2000 structure model grid diagram

表2 土层物理力学参数

SAP2000程序中提供了一种仅能受压的链接-支持单元，即缝单元(Gap)。链接单元连接两个节点，支持单元是一个单节点接地弹簧，两种单元的属性相同；每个单元假设由6个单独的“弹簧”组成，每个弹簧对应6个变形自由度中的一个(轴向、剪切、扭转和纯弯)。缝单元的非线性力-变形关系按下式确定：

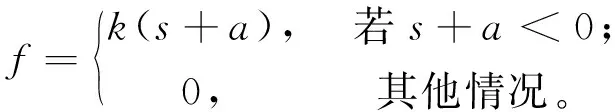
(13)

式中：s为弹簧内部变形；a为缝单元的初始张开量，必须为0或正值。

当缝单元的初始张开量为0时，若缝单元受压，即s+a=s<0，则缝单元受力为f=k·s，此时缝单元受力与受压弹簧的受力是一样的。若缝单元张开，即为f=0 的情况，表明缝单元不能受拉。这样，就可以采用缝单元模拟地层弹簧的力学行为。要注意到，使用缝单元模拟仅受压行为是需要指定其非线性刚度属性的。

此外，地层弹簧还与另一个关键问题相关，即地震反应位移也就是地震荷载的施加。通过试算比较发现，在SAP2000中，直接按地震反应土层位移施加即可，比较方便。难点在于将荷载施加在地层弹簧的远端节点。通过试算发现，如果使用单节点类型的缝单元，其模拟受压弹簧特性的局部坐标轴方向不易确定，易使人混淆。为此提出一种使用两节点缝单元+远端铰支座相组合模拟法向地层弹簧的方法。从结构单元节点沿垂直结构轴线的方向向外引出单位长度的线，为其指定缝单元属性，然后在该线的远端设置固定铰支座以模拟地层(图 2)。由于两节点形式缝单元的局部1轴始终沿其轴线方向，这样就不必担心缝单元元局部坐标轴方向的选择，而是可以对每个缝单元都直接指定局部1轴为法向地层弹簧刚度方向，不易出错。这个两节点缝单元的长度对计算结果没有影响，因为其受力仅与其刚度及压缩量有关，而与其长度无关。地震反应土层位移就可以直接施加在缝单元远端的铰支座上。

综上，在SAP2000中，采用只考虑受压的缝单元模拟结构与地层之间法向相互作用的压缩弹簧。至于结构与周围地层之间的切向相互作用，则采用常规既可受压又可受拉的土弹簧单元(Spring)模拟。

2.4 地层-结构有限元模型

采用PLAXIS 2D程序建立了动力时程分析有限元模型，如图 3所示，模型两侧采用自由场边界，底部采用柔性地基边界，在模型底部输入水平地震加速度时程记录，这里的地震波采用的是塔夫脱(Taft)波，水平地震加速度峰值调整至0.15g，同时根据对应的场地条件和设计地震动加速度反应谱曲线对输入地震波的周期也进行了相应调整，输入的水平地震动加速度时程曲线如图 4所示。

图3 动力时程分析有限元模型Fig.3 Dynamic time-history finite element model

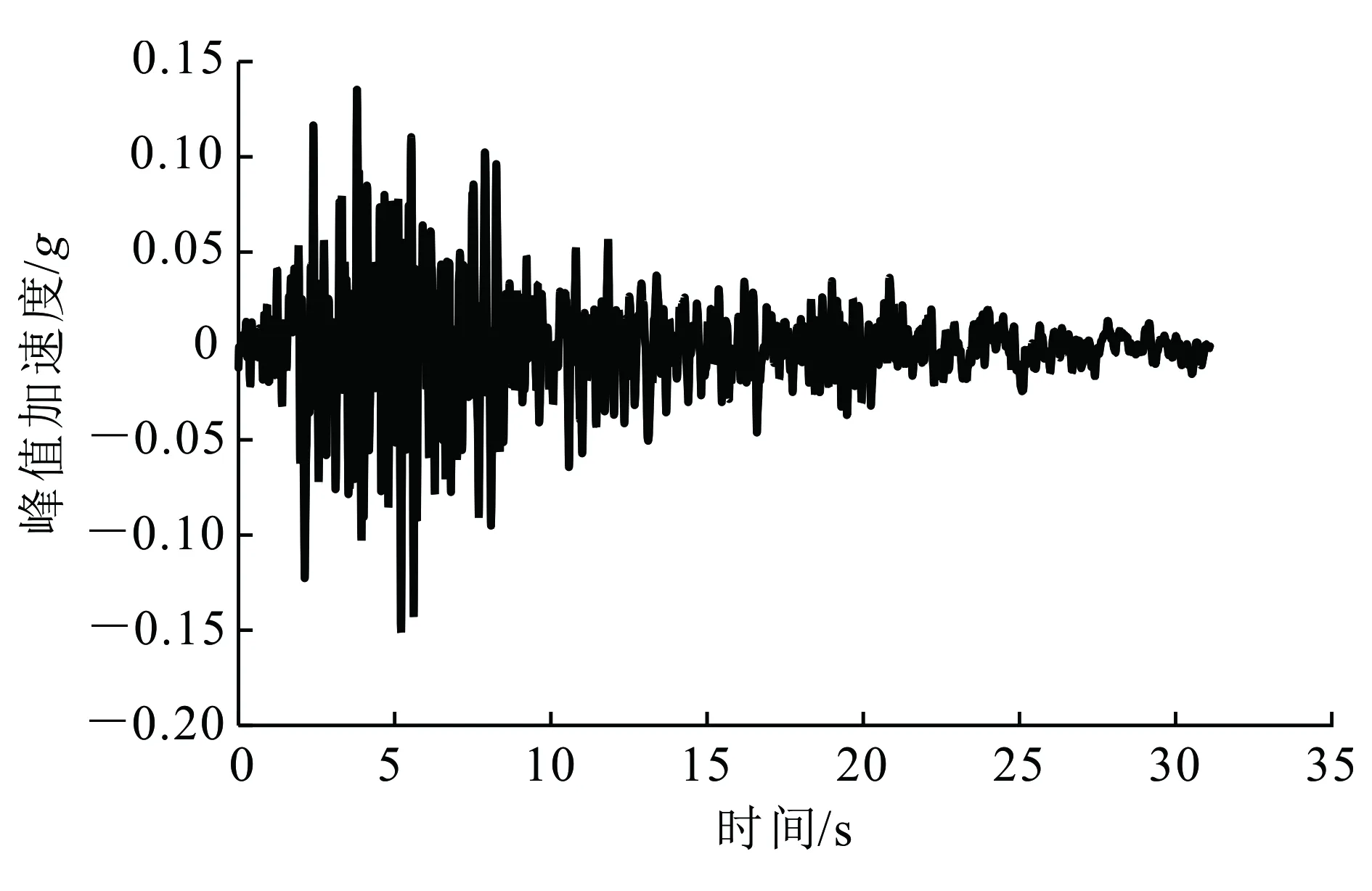
图4 输入的水平地震加速度时程曲线Fig.4 Input horizontal seismic acceleration time-history curve

2.5 土层等效计算过程

1)土层均质等效化处理

土层等效剪切波速vSd为

(14)

(15)

(16)

土层等效动变形模量Ed为

Ed=2(1+μ)Gd；

(17)

土层等效自振周期Ts为

(18)

式中：n为计算深度范围内土层的分层数；hi为计算深度范围内第i土层的厚度(m)；γi为计算深度范围内第i土层的重度；vSi为计算深度范围内第i土层的剪切波速(m/s)；μ为泊松比。

经计算，等效参数如下：

2)地基弹簧刚度

按日本经验公式计算得到

E0=133 843 kPa；Bv=5.8 m；Bh=4.8 m；Kvn=59 351 kN/m3；Kvt=19 783 kN/m3；Khn=99 817 kN/m3；Kht=33 272 kN/m3。

地基弹簧刚度如下：

kv=59 351lv；ksv=19 783lv；

kh=99 817lh；ksh=33 272lh。

其中：lv和lh分别为顶底板和侧墙弹簧间距(m)；kv和kh分别为顶底板和侧墙法向的地基弹簧刚度；ksv和ksh分别为顶底板和侧墙切向的地基弹簧刚度。

3)地层位移

根据城轨抗震规范[16]第5.2.1条，Ⅱ类场地在设计地震E2作用下的设计地震动峰值加速度amax=0.15g，设计地震动加速度反应谱特征周期Tg=0.45 s。设计地震动峰值位移umax=0.10 m。按土层地震反应位移沿深度呈余弦函数分布的假定，计算得到地下结构所处地层的地震反应位移；再根据土层相对位移转换为直接施加到结构上的等效荷载(表 3)。

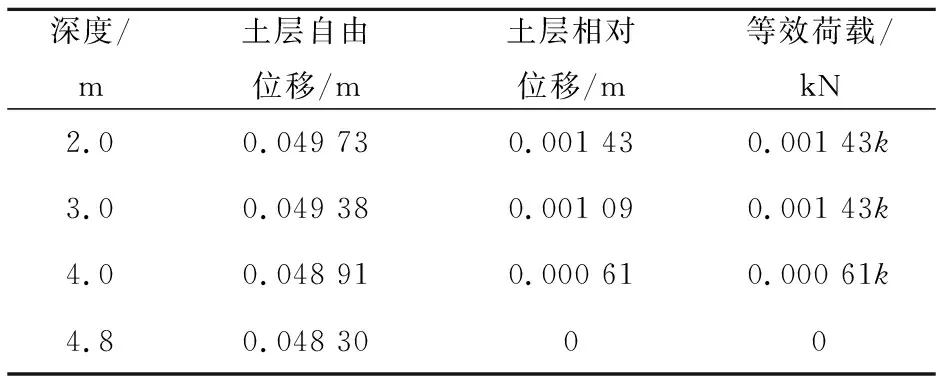
表3 设计土层地震反应位移

4)地震剪应力

按地震剪应力沿深度变化呈正弦函数的假定，以及假定顶底板剪应力均匀分布，计算得到结构顶底板及侧墙处地层剪应力如表 4所示。

表4 结构周围地层剪应力

5)结构地震惯性力

按经验公式计算得到结构惯性力为

f=0.142mg=0.142 ρVg。

式中，V为结构体积。

3 计算结果分析

3.1 计算方法合理性验证

地震荷载作用下双仓综合管廊结构典型变形形态如图 5所示，对应的缝单元的轴力如图 6所示。

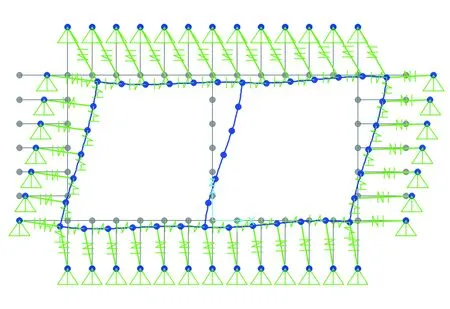
灰显的点、线表示综合管理廊变形前的结构模型网格。图5 结构位移变形网格图Fig.5 Grid diagram of structural displacement and deformation

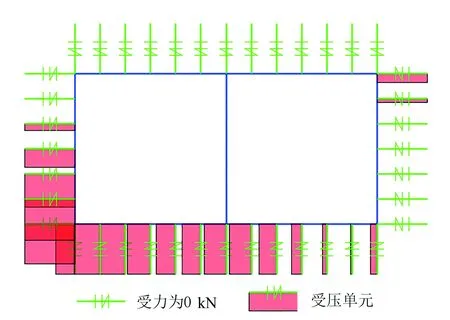
图6 缝单元轴力图Fig.6 Slot element axis diagram

结构变形对应的缝单元受力情况(图 6)表明，使用缝单元模拟法向地层弹簧达到了预期的效果，仅受压不受拉，恰当地反映了结构周围土体对结构的约束效应。结合图 5所示的结构变形可以发现，在缝单元远端施加土层相对位移所引起的结构位移与土层位移并不完全同步，这恰好体现了土与结构刚度差异所导致的非同步相互作用。此外，通过计算比较发现，在缝单元远端施加强制位移与将土层相对位移转换成等效节点荷载之后直接施加在结构节点上的效果是不同的。此处建议采用施加远端强制位移的方法。

3.2 基床系数的不同算法对结构地震反应的影响

在相同的外荷载条件下(土层相对位移和结构周边剪应力相同)，考虑土体分层与土层等效处理计算基床系数的不同，并引入“李亮法”与规范法的计算方法，最终得到的弯矩如表5所示(参照图7编号示意图)。在结构关键部位设置内力监测点，如图 8所示，各监测点内力峰值汇总于表6、表7。

从表6和表7可以看到，不同的基床系数计算方法，最终得到的结构内力峰值及峰值出现的部位均有所变化。利用经验公式计算基床系数与静力有限元法计算基床系数得到的最终结构内力有一定差距，前者最终得到的轴力和剪应力峰值比后者偏大，而弯矩峰值则比后者偏小。

3.3 地层剪应力的不同算法对结构地震反应的影响

土体分层除了对结构顶、底板处地基基床系数的取值有影响之外，还由于相应土层的动剪切模量的不同，导致根据剪应力正弦分布公式计算得到的顶、底板处地层剪应力也与等效土层的情况有所不同。以本算例来说，土层等效处理后的等效动剪切模量为55 768 kPa，据此计算的顶、底板地层剪应力分别为15.26 kPa和37.79 kPa；而考虑土体分层后，管廊结构处于第一层人工填土和第二层粉质黏土层中，下部刚度较大的残积砂质黏性土对结构周围地层剪应力的影响很小，此时根据剪切波速计算出的结构顶、底板处土层动剪切模量分别为32 805.00 kPa和19 143.00 kPa，相应的顶、底板处地层剪应力为8.98 kPa和12.97 kPa。可见，对于土层刚度或者说剪切波速相差较大的情况，如果仍然进行均质等效化处理可能引起较大误差，尤其是从施加到结构上的外荷载方面就已经与实际产生较大偏差。按照上述考虑分层后得到的地层剪应力作为外荷载重新进行计算，结果如表8所示(参照图7编号示意图)。关键部位内力峰值汇总见表9、表10，表中同时给出了非线性有限元动力时程法的计算结果，作为对比。注意，此处仅考虑地震作用引起的附加内力。

表5 基床系数不同计算方法得到的地震荷载作用下结构弯矩

Table 5 Bending moment of structures subjected to seismic loads calculated with different moduli of subgrade reactionkNm/m

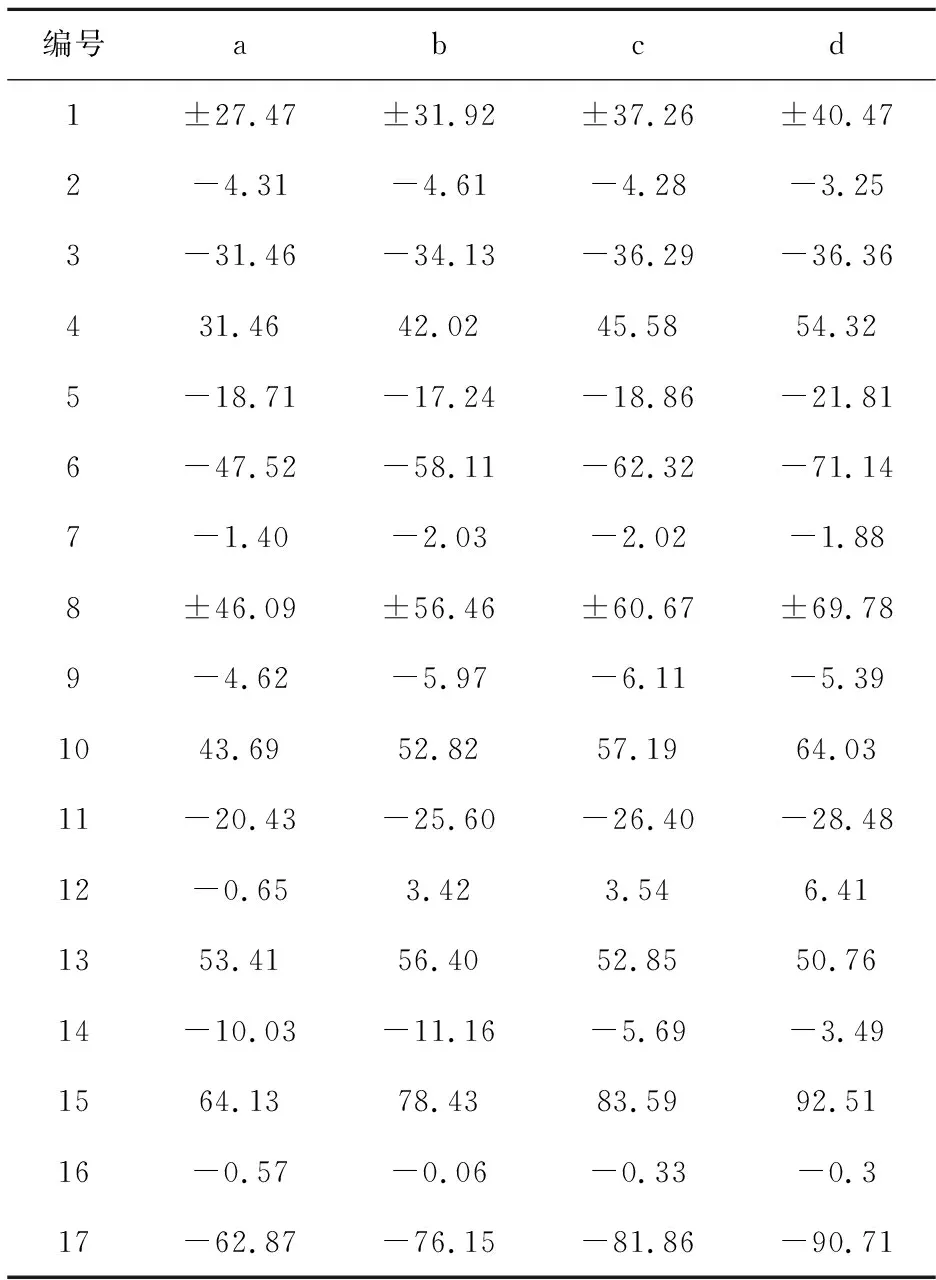
表5 基床系数不同计算方法得到的地震荷载作用下结构弯矩

编号abcd1±27.47±31.92±37.26±40.472-4.31-4.61-4.28-3.253-31.46-34.13-36.29-36.36431.4642.0245.5854.325-18.71-17.24-18.86-21.816-47.52-58.11-62.32-71.147-1.40-2.03-2.02-1.888±46.09±56.46±60.67±69.789-4.62-5.97-6.11-5.391043.6952.8257.1964.0311-20.43-25.60-26.40-28.4812-0.653.423.546.411353.4156.4052.8550.7614-10.03-11.16-5.69-3.491564.1378.4383.5992.5116-0.57-0.06-0.33-0.317-62.87-76.15-81.86-90.71

注：a.日本公式法(等效均质)；b.日本公式法(分层)；c.规范静力有限元法(分层)；d. “李亮法”(分层)。

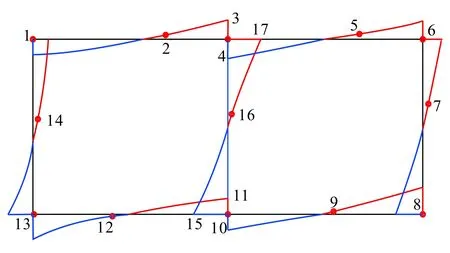
注：蓝色可表示正弯矩，红色可表示负弯矩，以表5和表8中的数值为准。图7 基床系数不同计算方法得到的地震荷载作用下结构弯矩编号示意图Fig.7 Schematic diagram of structural bending moment under different earthquake loads caused by different subgrade coefficients

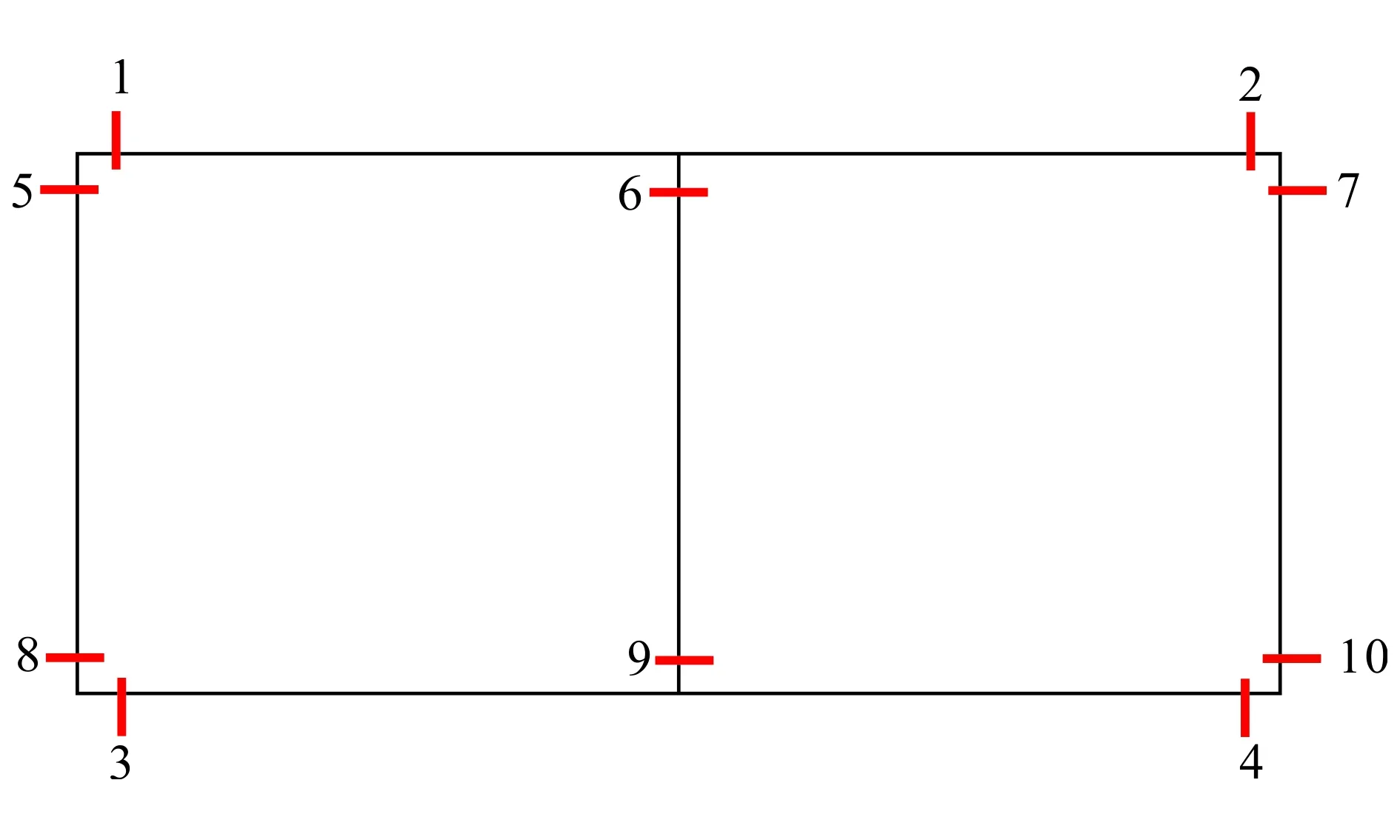
图8 结构内力取值点位示意Fig.8 Point location diagram of evaluation of structural internal force

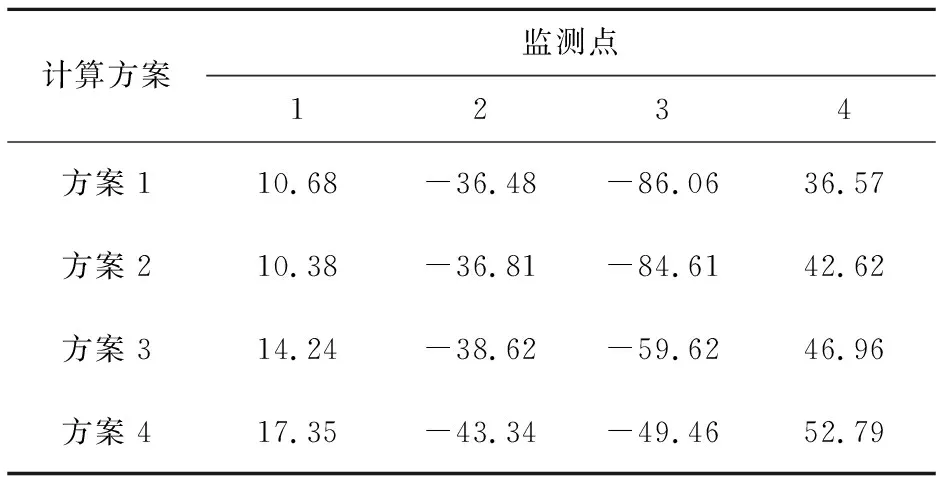
表6 等效土层计算地层剪应力后基床系数不同计算方法得到的结构轴力峰值

注：方案1—方案4见表 1。

以非线性有限元动力时程分析方法(方案8)的计算结果作为基准值，将各种简化方法的结构内力计算结果与基准值进行比较，获得各简化方法的内力结果相对误差，汇总于表 11。

从表11可以看出，与方案8的计算结果作为对比，方案1--方案4的内力计算结果相对误差显著偏大。计算可知，以监测点3的轴力计算误差为例，方案1—方案4的相对误差为-400%～-250%，而方案5—方案7的相对误差均在-60%以内。前4种方案与后3种方案的重要差别就在于土层的简化处理程度，前4种方案均采用均质等效化处理计算地层剪应力，上述结果说明这样的处理方法误差偏大，地层剪应力宜分层计算。

通过上述计算结果分析，可以认为：1)计算深度内土层刚度分布差异较大时，应该考虑土体分层特性计算土层弹簧刚度及动剪切模量等参数。2)在假设土层位移沿深度按余弦函数分布、地层剪应力按正弦函数分布的条件下，按日本公式法、规范静力有限元法和“李亮法”计算基床系数最终得到的结构内力与动力时程法的结构内力相比，在结构的不同部位其大小不同。以本例来说，这几种方法的计算结果总体差别不大，也就是说在一定条件下现行简化算法的计算结果还是比较合理的。3)“李亮法”最终结构内力与日本公式法和规范法相比，相对动力时程法的结果偏差要稍大一些，笔者认为在初步的粗略估算时可以采用，但不宜单独作为最终结果依据。

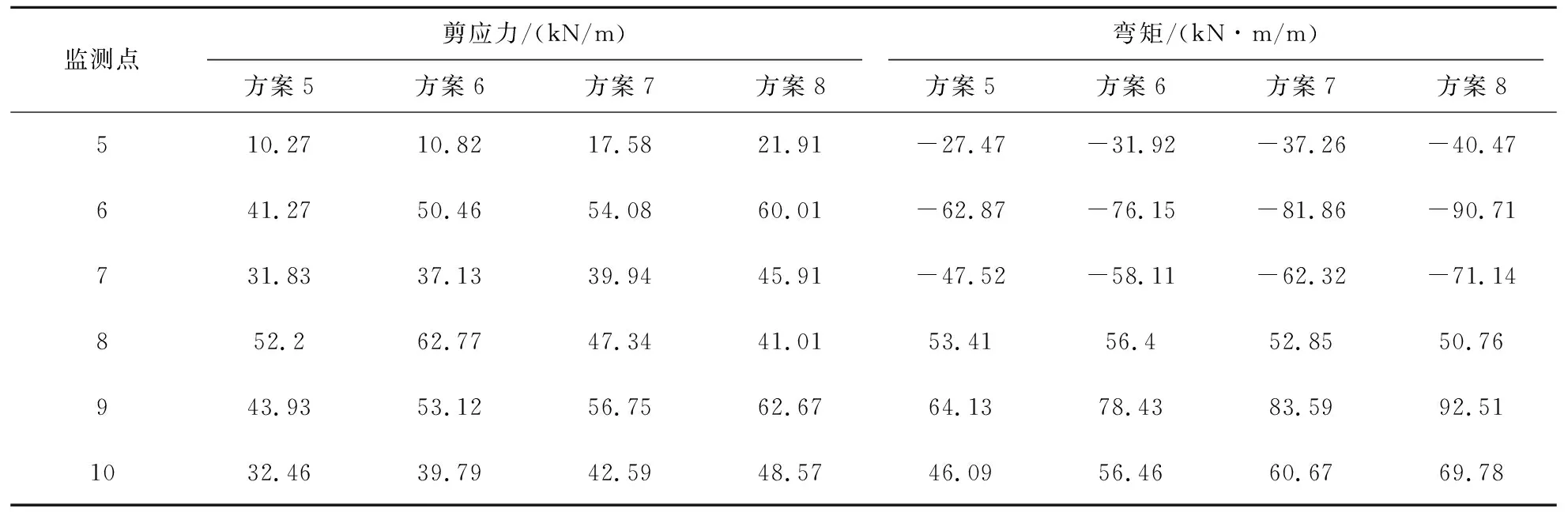
表7 等效土层计算地层剪应力后基床系数不同计算方案得到的结构剪应力及弯矩峰值

注： 方案5—方案8见表 1。

表8 分层计算剪应力后基床系数不同计算方法得到的地震荷载作用下结构弯矩

Table 8 Bending moment of structures subjected to seismic loads calculated with different moduli of subgrade reaction based on the calculation of shear stress in a stratified soil masskNm/m

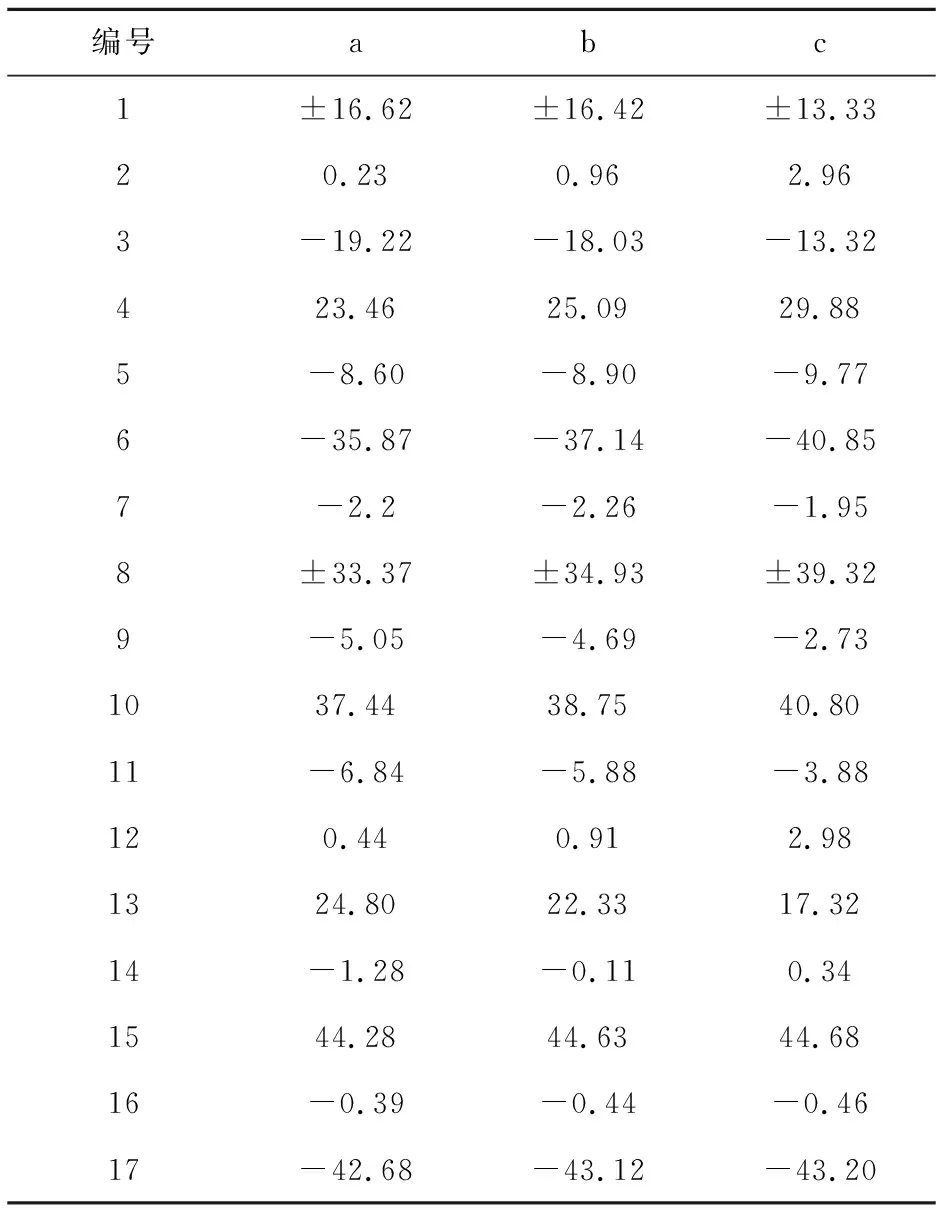
表8 分层计算剪应力后基床系数不同计算方法得到的地震荷载作用下结构弯矩

编号abc1±16.62±16.42±13.3320.230.962.963-19.22-18.03-13.32423.4625.0929.885-8.60-8.90-9.776-35.87-37.14-40.857-2.2-2.26-1.958±33.37±34.93±39.329-5.05-4.69-2.731037.4438.7540.8011-6.84-5.88-3.88120.440.912.981324.8022.3317.3214-1.28-0.110.341544.2844.6344.6816-0.39-0.44-0.4617-42.68-43.12-43.20

注：a.日本公式法(分层)；b.规范静力有限元法(分层)；c.“李亮法”(分层)。

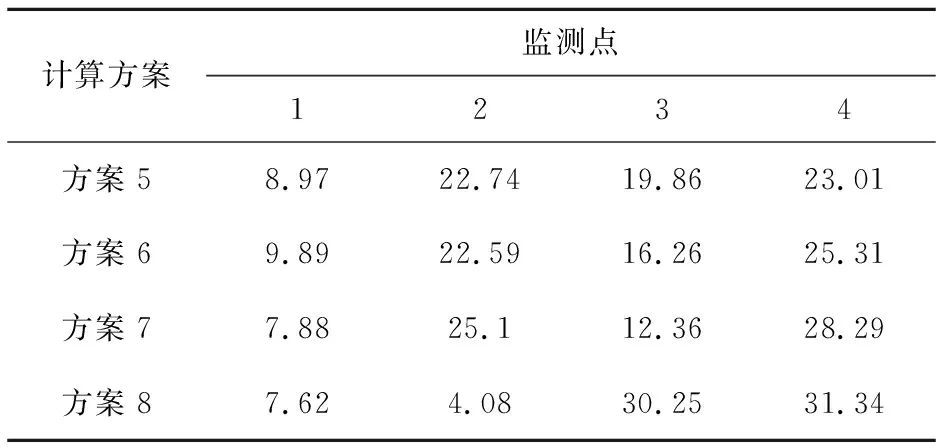
表9 分层计算剪应力后基床系数不同计算方案得到的结构轴力峰值

注：方案5—方案8见表 1。

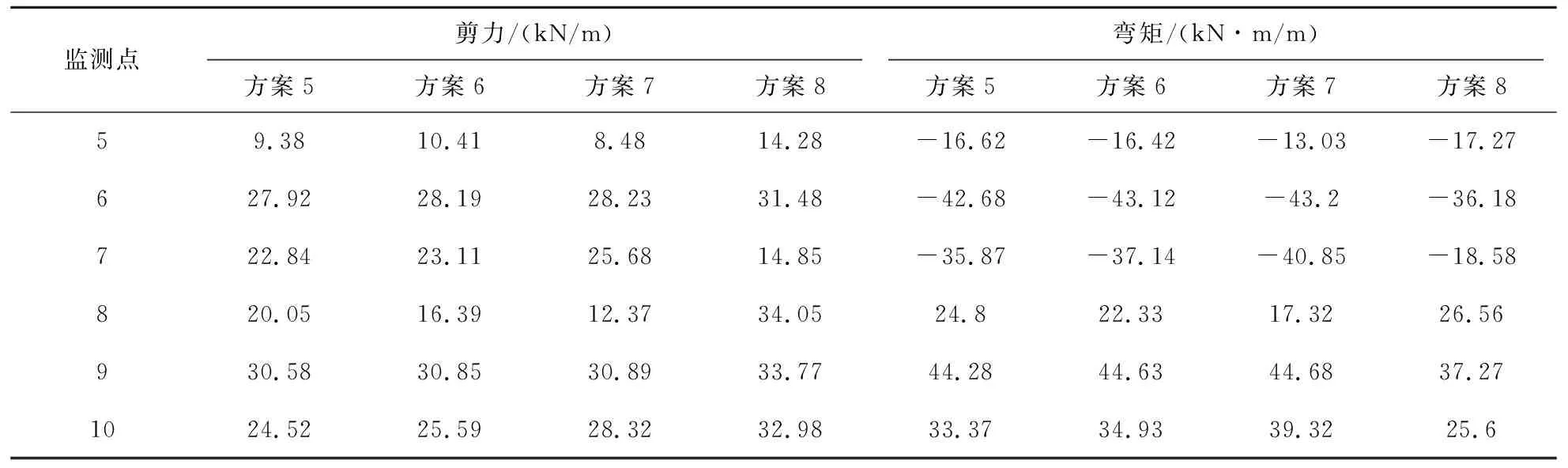
表10 分层计算剪应力后基床系数不同计算方案得到的结构剪应力及弯矩峰值

注：方案5—方案8见表 1。

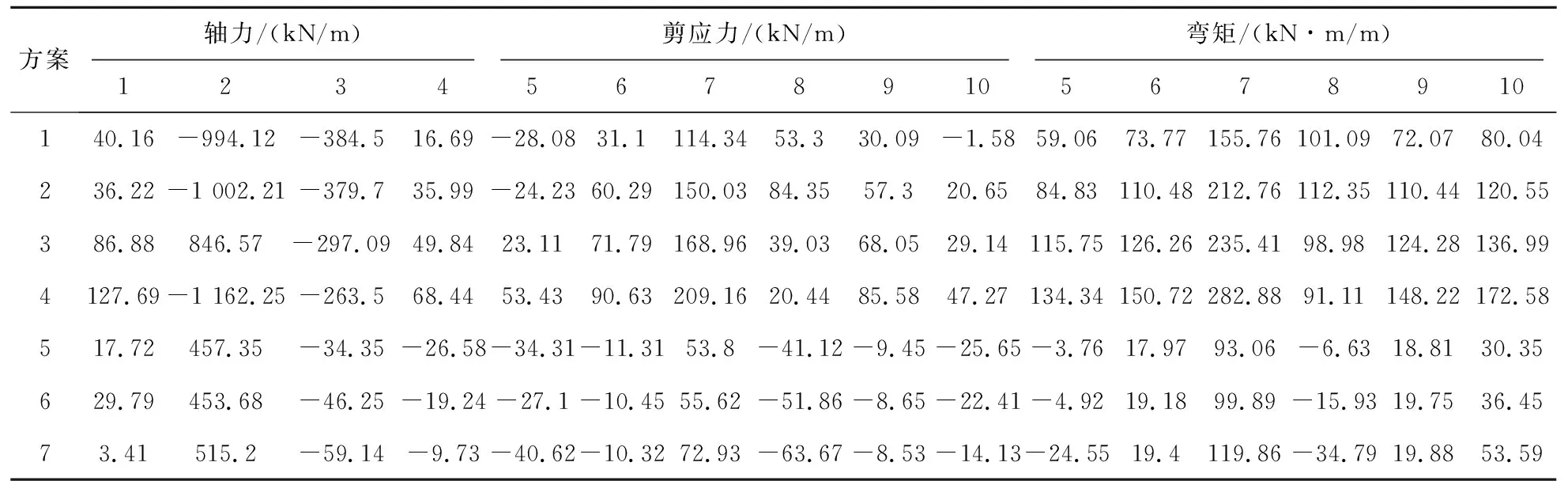
表11 各种简化方法相对动力时程法(方案8)的内力计算误差

4 结论

1)综合考虑计算实施复杂程度、计算效率和计算精度，反应位移法的实施难度较低，并且其各项所需计算参数及地震荷载等均有一些相应的简化方法可供参考借鉴，尤其在初步的抗震计算中可优先选用。

2)反应位移法的关键之一是地基弹簧刚度的确定，推荐使用日本公式法和常规的静力有限元法。在计算地基弹簧刚度和土体的动力参数时，应尽量考虑土体分层情况，若一味进行均匀等效化处理，可能导致土体动剪切模量偏大，进而使得地基弹簧刚度和地层剪应力的计算结果产生较大偏差。

3)管廊结构地震反应计算中需施加仅受压的地基弹簧模拟土与结构相互作用，可采用SAP2000程序中可实现仅受压力学行为的两节点缝单元+远端固定铰支座相结合的方法模拟法向地基弹簧，采用常规土弹簧单元模拟切向地基弹簧，并且选择非线性计算类型以实现缝单元的非线性仅受压特性。

4)地层剪应力可按分布情况直接施加在结构梁单元上，结构惯性力不宜按集中力施加，也应按结构质量分布特点沿整个结构均匀施加。

5)地震荷载宜直接按土层相对位移施加在缝单元的远端铰支座上，而无需再进行等效节点荷载的换算，这样可免去在被动侧结构上施加指向土体内部的等效节点荷载所带给人的困扰。