产品差异化竞争对供应链合作广告的影响研究

尚豫新 孙曰瑶

一、引言

广告可以分为制造商的全国性广告和零售商的地区性广告两种形式，全国性广告可以提升产品知名度，地区性广告可以直接增加消费者需求[1]。纵向合作广告模式是指零售商在产品销售活动中，其地区性广告的部分成本由制造商来负担的一种供应链合作模式，制造商可以通过合作广告的方式使零售商加大对其产品的销售力度进而刺激消费者需求，产品销量的增加使双方达到合作共赢[2-3]。以美国为例，2010年美国有75个行业采用合作广告销售模式，销售额达到8 020亿美元[4]。合作广告支出也是制造商营销预算的重要内容，美国制造商花在合作广告上的费用1970年为90亿美元，2000年为150亿美元，2010年达到500亿美元[5-6]。在消费者需求多样化与产品买方市场的今天，制造商之间争夺市场份额的竞争也日趋激烈，零售超市里不同品牌的饮料、奶粉、化妆品等都围绕消费者展开了激烈的争夺。为了提高产品的市场占有率，制造商们纷纷使用产品差异化策略并与零售商进行广告合作来开拓市场。在这种情形下，合作广告作为制造商的一项主要投资，合作广告的最优分担比例是多少？产品差异化程度对合作广告的分担比例会有怎样的影响？这些都是制造商非常关心的问题。但是，目前还没有产品差异化竞争对供应链合作广告影响方面的研究。笔者从这个角度切入，研究产品差异化竞争情形下由两个制造商与一个共同零售商组成的供应链中合作广告的最优投入问题，并分析产品差异化程度对供应链中各方合作广告投入的影响。

二、研究综述

近年来关于供应链中制造商与零售商的协作问题逐渐成为研究热点，合作广告方面的问题也备受关注。

针对合作广告的研究方法可分为静态研究和动态研究。静态研究方法主要为静态博弈，相关文献主要有：Berger(1973)[7]最早使用数理模型研究了供应链中制造商与零售商的合作广告问题；Dant和Berger(1996)[8]研究了制造商与零售商合作情形下制造商的合作广告最优分担率，得出合作广告策略可以实现双赢；Jørgensen等(2001)[9]研究得出合作广告策略可以帮助供应链各方实现利润的帕累托改进；吴文清等(2006)[10]探讨了单一制造商与零售商在市场需求不确定情况下，Nash博弈与Stackelberg博弈下的合作广告问题；王圣东和周永务(2008)[11]分析了制造商在直销与零售双渠道营销模式下与零售商的合作广告问题并给出了双方合作广告分摊策略；黄松等(2011)[12]研究了直销与零售双渠道供应链中的合作广告问题，得出制造商最优合作广告分担比例与消费者对不同渠道的偏好程度有关；浦徐进等(2016)[13]构建了制造商与零售商销售两种互补品的供应链Stackelberg博弈模型，得出当捆绑折扣价格敏感系数较大时零售商应选择捆绑销售策略来出售互补品；吴正祥和李宝库(2017)[14]研究了利他偏好下制造商与零售商的供应链协调问题。动态研究反映了时间的动态特征，主要方法为演化博弈与微分方程，相关文献主要有：单汨源等(2009)[15]使用演化博弈的方法分析了制造商与零售商组成供应链的合作广告问题；吕芹和霍佳震(2011)[16]分析了零售商同时销售自己品牌商品和制造商品牌商品模式下的合作广告问题，得出Stackelberg博弈时零售商与制造商的利润均高于非合作博弈时的利润；张旭梅和陈国鹏(2016)[17]研究了单一制造商使用品牌差异策略在直销与零售双渠道销售产品时与零售商的合作广告问题；陈国鹏等(2017)[18]使用随机微分模型研究了制造商与零售商合作广告投入问题；陈东彦等(2017)[19]分析了广告延时效应下的供应链合作广告策略。上述文献分析了不同情况下供应链中各方在合作广告时的最优策略，取得了比较丰富的科研成果，但是研究中存在一个明显的不足，就是相关研究都是以单一制造商与单一零售商的模式为研究对象，并没有分析供应链中存在多个制造商与零售商的情况，因此研究具有较大的局限性。

只有个别学者研究了单一制造商与多零售商之间的合作广告问题。熊中楷等(2010)[20]使用随机微分模型研究了单一制造商与两个零售商的合作广告投入问题；Wang等(2011)[21]分析了单一制造商与两个零售商的不同竞争模式对合作广告策略的影响；陆媛媛(2011)[22]研究了单一制造商与多个互相竞争零售商的合作广告策略。这些文献虽然拓宽了合作广告的研究视野，但与现实中制造商之间也存在广泛竞争的情形相比，这些理论模型与现实还是有较大差距。

在消费者需求多样化与制造商激烈竞争的市场经济中，产品差异化竞争的情形在现实中更加普遍，当制造商们存在差异化竞争的产品在面对共同的零售商时，制造商是否要与零售商采取合作广告策略？产品差异化程度对制造商与零售商的合作广告投入以及最终利润有何影响？这些都是急需研究的现实问题，而以往相关研究对这种情形的解释力与说服力就显得力不从心。基于这种情形，本文建立存在产品差异竞争的双制造商供应链系统，运用Hamilton-Jacobi-bellman方程来研究产品差异化竞争下的非合作博弈广告问题与Stackelberg博弈合作广告问题，分析产品差异化程度对供应链中各方合作广告投入的影响。更具体地说就是：其一，相对于以往文献中只针对一个制造商与零售商之间合作广告的分析，我们通过对两个竞争性制造商与零售商之间合作广告的投入进行分析，以便使研究更加贴近现实；其二是我们分析了产品差异程度的变化对供应链中各方合作广告的投入和分担比例的影响，使研究更具有解释力。

三、产品差异化竞争下供应链合作广告分析

(一)模型结构与假设

产品差异化竞争供应链模型由两个制造商(制造商1与制造商2)和一个共同的零售商构成，两个制造商生产同种类型但存在一定差异的产品，并通过零售商对消费者进行销售，产品之间存在替代性竞争，两个制造商在各自进行全国性广告的同时还以合作广告的形式分担零售商地区性广告的部分成本(图1)。

图1 产品差异化竞争供应链模型

1.三方的广告投入与成本。

2.制造商的商誉。

与Amrouche等(2008)[24]的研究类似，商誉的变化采用Nerlove-Arrow模型，制造商1、制造商2和零售商的广告投入都会增加制造商的商誉，用如下微分方程反映两个制造商商誉随时间的变化：

dGm1(t)/dt=λrIr1(t)+λmIm1(t)-δGm1(t)

dGm2(t)/dt=λrIr2(t)+λmIm2(t)-δGm2(t)

其中Gm1(t)和Gm2(t)分别表示制造商1和制造商2的商誉，λm、λr和δ为系数且均大于零，其中δ为商誉衰减系数。

3.产品的需求函数。

制造商和零售商的广告投入以及产品差异程度都会影响消费者的产品需求，由于本文研究产品差异程度对供应链合作广告的影响，分析产品差异化作用于零售商地区性广告投入而对消费者需求产生的影响，故产品差异化对制造商全国性广告投入的影响不属于文本的讨论范畴。在Jørgensen等(2001)[9]、熊中楷等(2010)[20]和Jørgensen等(2000)[23]研究的基础上对需求函数进行扩展，消费者对制造商1和制造商2产品的即时需求量Q1(t)和Q2(t)分别用函数表示为：

Q1(t)=αGm1(t)+βIr1(t)+ηIm1(t)

+k(Ir1(t)-Ir2(t))

Q2(t)=αGm2(t)+βIr2(t)+ηIm2(t)

-k(Ir1(t)-Ir2(t))

其中：α(α>0)表示制造商商誉G(t)对消费者需求的影响；β(β>0)表示零售商地区性广告投入Ir(t)对消费者需求的影响；η(η>0)表示制造商全国性广告投入Im(t)对消费者需求的影响；k(k>0)表示两种产品的差异程度，k越大表示两种产品差异程度越大，会使零售商在不同产品间广告投入的差异引发的消费者需求量的差异越大。

4.三方的边际利润。

设三方具有相同的贴现率ρ(ρ>0)，制造商1和制造商2的边际利润分别为φ1和φ2，零售商销售两种产品的边际利润分别为φ3和φ4，边际利润均为正值。

(二)制造商与零售商非合作博弈模型

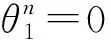
命题1：非合作博弈时各方的最优广告策略为：

(1)

(2)

(3)

(4)

+ηIm1(t)+k(Ir1(t)-Ir2(t))]

+λmIm1(t)-δGm1(t))}

(5)

为使式(5)右端最大化，求解其对Im1的一阶偏导并等于零可得：

(6)

(7)

比较式(7)两边的系数，求出系统最优利润函数的参数值为：

(8)

将式(8)代入式(6)得到式(1)。

+ηIm2(t)-k(Ir1(t)-Ir2(t))]

+λmIm2(t)-δGm2(t))}

(9)

式(9)对Im1求偏导可得：

(10)

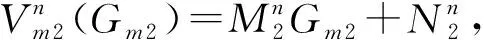
(11)

比较式(11)两边的系数，求出系统最优利润函数的参数值为：

(12)

将式(12)代入式(10)可得式(2)。

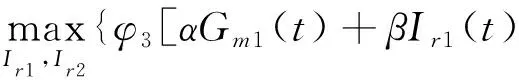
+ηIm1(t)+k(Ir1(t)-Ir2(t))]

+φ4[αGm2(t)+βIr2(t)

+ηIm2(t)-k(Ir1(t)-Ir2(t))]

+∂Vr(Gm1,Gm2)/∂Gm1(λrIr1(t)

+λmIm1(t)-δGm1(t))

+∂Vr(Gm1,Gm2)/∂Gm2(λrIr2(t)

+λmIm2(t)-δGm2(t))}

(13)

式(13)对Ir1和Ir2求偏导可得：

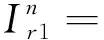
+λ∂Vr(Gm1,Gm2)/∂Gm1r]/μ

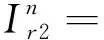
+λr∂Vr(Gm1,Gm2)/∂Gm2]/μ

(14)

(15)

比较式(15)两边的系数，求出系统最优利润函数的参数值为：

(16)

将式(16)代入式(14)，可得式(3)与式(4)。证毕。

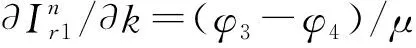
推论1：在非合作博弈情况下，当产品差异程度增大时，零售商会在边际利润较高的渠道加大广告投入，同时在边际利润较低的渠道降低广告投入，但零售商广告最优总投入不受产品差异程度的影响。

推论2：在非合作博弈情况下，零售商对产品的最优广告投入随着本产品零售渠道边际利润的提高而增加，随着竞争产品零售渠道边际利润的提高而减少。

(三)制造商与零售商Stackelberg博弈模型

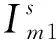
命题2：Stackelberg博弈时各方的最优广告策略为：

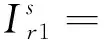
+(φ1+φ3/2)αλr/(ρ+δ)]/μ

(17)

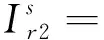
+(φ2+φ4/2)αλr/(ρ+δ)]/μ

(18)

(19)

(20)

(21)

其中，X1=φ1(β+k)+φ1αλr/(ρ+δ)，Y1=φ3(β+k)-φ4k+φ3αλr/(ρ+δ)。

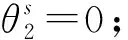
(22)

其中，X2=φ2(β+k)+φ2αλr/(ρ+δ)，Y2=φ4(β+k)-φ3k+φ4αλr/(ρ+δ)。

证明：零售商利润函数Vr(Gm1,Gm2)的HJB方程为:

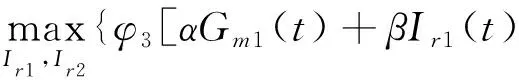
+ηIm1(t)+k(Ir1(t)-Ir2(t))]

+φ4[αGm2(t)+βIr2(t)

+ηIm2(t)-k(Ir1(t)-Ir2(t))]

+∂Vr(Gm1,Gm2)/∂Gm1(λrIr1(t)

+λmIm1(t)-δGm1(t))

+∂Vr(Gm1,Gm2)/∂Gm2(λrIr2(t)

+λmIm2(t)-δGm2(t))}

(23)

式(23)对Ir1和Ir2求偏导可得：

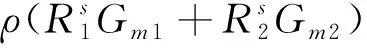
=[φ3(β+k)-φ4k

+λr∂Vr(Gm1,Gm2)

/∂Gm1]/[(1-θ1)μ]

(24)

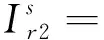
+λr∂Vr(Gm1,Gm2)/∂Gm2]/[(1-θ2)μ]

(25)

(26)

比较式(26)两边的系数，求出系统最优利润函数的参数值为：

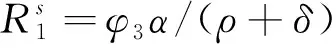
(27)

制造商1的HJB方程为：

+ηIm1(t)+k(Ir1(t)-Ir2(t))]

+λmIm1(t)-δGm1(t))}

(28)

将式(24)和式(25)带入式(28)并对Im1求偏导可得：

(29)

(30)

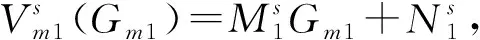
(31)

比较式(29)两边的系数，求出系统最优利润函数的参数值为：

(32)

将式(32)代入式(29)可得式(19)。

制造商2的HJB方程为：

+ηIm2(t)-k(Ir1(t)-Ir2(t))]

+λmIm2(t)-δGm2(t))}

(33)

将式(24)和式(25)带入式(33)并对Im1求偏导可得：

(34)

(35)

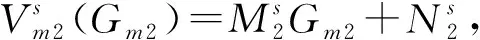
(36)

比较式(36)两边的系数，求出系统最优利润函数的参数值为：

(37)

将式(37)代入式(34)可得式(20)。把式(27)、式(32)和式(37)分别代入式(30)和式(35)可得式(21)和式(22)，把式(27)和式(21)代入式(24)可得式(17)，再把式(27)和式(22)代入式(25)可得式(18)。证毕。

1.分析产品差异程度与边际利润对零售商广告投入的影响。

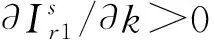
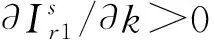
图2 两种产品边际利润的分布

推论3：在Stackelberg博弈时，产品差异程度对零售商最优广告投入的影响取决于渠道边际利润的相对大小。

推论4：在Stackelberg博弈时，零售商对产品最优广告投入随着本产品制造商边际利润和零售边际利润的提高而增加，随着竞争产品零售边际利润的提高而减少。

2.分析制造商对零售商广告合作的策略并研究产品差异程度与制造商边际利润对制造商合作广告分担比例的影响。

由命题2可知供应链系统中制造商对零售商的合作广告策略可以分为四种情况：

表1 制造商与零售商的合作广告策略

分析产品差异程度对制造商合作广告分担比例的影响。先分析产品差异程度k(k>0)对制造商1与零售商广告合作的影响，由式(21)整理可得2X1-Y1=(2φ1+φ4-φ3)k-(φ3-2φ1)[β+αλr/(ρ+δ)]，可分三种情况进行讨论：

第一，当2φ1+φ4<φ3时，无论k取何值都有2X1-Y1<0，故制造商1广告策略为不合作。

第二，当2φ1<φ3<2φ1+φ4时，又可分为两种情况：当0(φ3-2φ1)[β+αλr/(ρ+δ)]/(2φ1+φ4-φ3)时，得到2X1-Y1>0，制造商1广告策略为合作。

第三，当φ3<2φ1时，无论k取何值都有2X1-Y1>0，故制造商1广告策略为合作。

再分析产品差异程度k(k>0)对制造商2与零售商广告合作的影响，由式(22)整理可得2X2-Y2=(2φ2+φ3-φ4)k-(φ4-2φ2)[β+αλr/(ρ+δ)]，可分三种情况进行讨论：

第一，当2φ2+φ3<φ4时，无论k取何值都有2X2-Y2<0，故制造商2广告策略为不合作。

第二，当2φ2<φ4<2φ2+φ3时，又分为两种情况：当0(φ4-2φ2)[β+αλr/(ρ+δ)]/(2φ2+φ3-φ4)时，得到2X2-Y2>0，制造商2广告策略为合作。

第三，当φ4<2φ2时，无论k取何值都有2X2-Y2>0，故制造商2广告策略为合作。

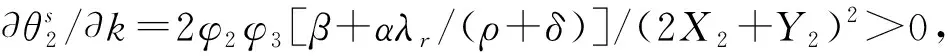
推论5：在Stackelberg博弈时，制造商与零售商在供应链中边际利润的相对大小是决定双方是否进行广告合作的主要因素，产品差异程度是决定双方是否进行广告合作的次要因素，只有制造商与零售商的边际利润在特定区域内，产品差异程度才能决定双方是否进行广告合作。

推论6：Stackelberg博弈中制造商与零售商广告合作的情况下，两个制造商对零售商合作广告的分担比例都随产品差异程度的增加而提高。

推论7：Stackelberg博弈中制造商边际利润对其合作广告分担比例的影响，与产品差异程度以及零售商渠道边际利润密切相关。

(四)两种博弈的比较分析

1.两种博弈下零售商最优广告投入的比较。

推论8：零售商Stackelberg博弈与非合作博弈中广告投入之差随着产品差异程度的增加而增大。

2.两种博弈时各方的利润分析。

四、两种博弈模型的算例分析

把制造商1边际利润φ1与产品差异程度k作为变量，保持其他参数值不变，研究Stackelberg博弈时制造商1对零售商广告成本分担比例θ1的变化(图3)。由图3可知，在三个变量均为正值的情况下，制造商1对零售商广告成本分担比例θ1随自己边际利润φ1的增加而增大，也随产品差异程度k的增加而增大。再把制造商2边际利润φ2与产品差异程度k作为变量，保持其他参数值不变，研究Stackelberg博弈时制造商2对零售商广告成本分担比例θ2的变化(图4)。由图4可知，在三个变量均为正值的情况下，制造商2对零售商广告成本分担比例θ2随自己边际利润φ2的增加而增大，也随产品差异程度k的增加而增大。结果与推论5、6和7一致。

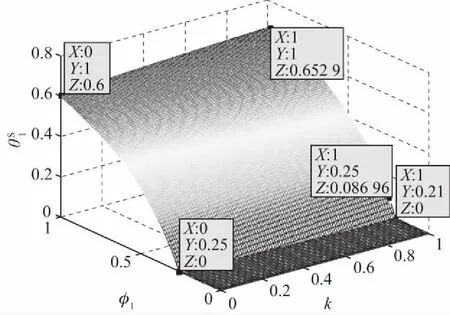
图3 Stackelberg博弈时φ1与k对制造商1广告成本分担比例θ1的影响

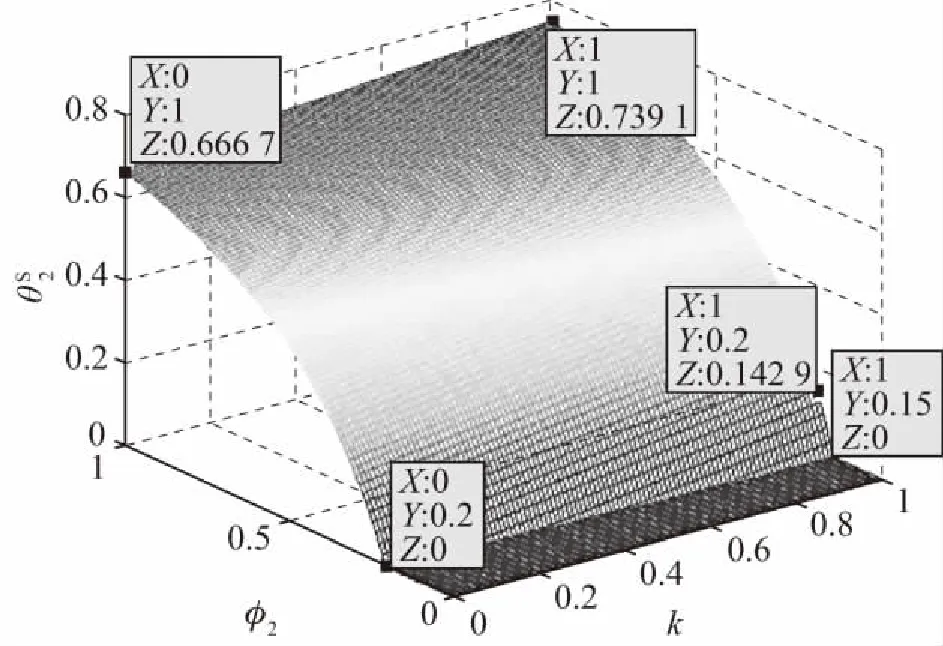
图4 Stackelberg博弈时φ2与k对制造商2广告成本分担比例θ2的影响

把产品差异程度k作为变量，保持其他参数值不变，研究非合作博弈与Stackelberg博弈时产品差异程度k对制造商1、制造商2与零售商利润的影响(图5和图6)。由图5可知在非合作博弈时，具有边际利润优势的制造商1与零售商的利润随产品差异程度k的增大而增加，而处于边际利润劣势的制造商2的利润随产品差异程度k的增大而减小。由图6可知，在Stackelberg博弈时具有边际利润优势的制造商1与零售商的利润随产品差异程度k的增大而增加，而处于边际利润劣势的制造商2的利润随产品差异程度k的增大而减小。

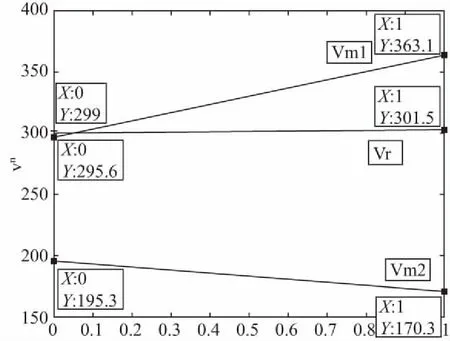
图5 非合作博弈时k对制造商与零售商利润的影响

图6 Stackelberg博弈时k对制造商与零售商利润的影响

图7 非合作博弈与Stackelberg博弈时k>对三方总利润的影响

分析非合作博弈与Stackelberg博弈时产品差异程度对三方总利润的影响(图7)，由图7可知随着产品差异程度k的增加，Stackelberg博弈时供应链总利润总是高于非合作博弈时供应链总利润，两种模式中供应链总利润都随产品差异程度k的增大而增加并且Stackelberg博弈时供应链总利润的增加更明显。

五、结论与展望

(一)研究结论

本文分析了产品差异化对供应链合作广告的影响，建立产品差异化模型并运用Hamilton-Jacobi-bellman方程分别分析了制造商与零售商非合作博弈时广告投入，Stackelberg博弈时广告投入与合作广告分担比例，并对两种博弈进行了比较。通过对产品差异化情形下供应链合作广告的模型分析，笔者发现并因此得出相关结论和管理启示。

1.在非合作博弈时，随着产品差异程度的增大，零售商对产品的最优广告投入会从边际利润低的零售渠道向边际利润高的零售渠道转移。说明对于不同制造商的产品而言，产品差异程度的变化的确会影响到零售商在不同产品销售中的广告投入水平，产品差异程度越大，零售商在边际利润高的渠道的广告投入就越多，促销力度也越大。所以在零售渠道边际利润较高的产品的制造商应该努力提高自己产品与同类产品的差异程度，进而使零售商的广告投入更多地向自己的产品倾斜。

2.在Stackelberg博弈时，产品差异程度也是决定制造商与零售商双方是否进行广告合作的影响因素。在一定条件下，随着产品差异程度的增加，制造商与零售商之间的广告情形会从“不合作状态”转换为“合作状态”。并且在制造商与零售商进行广告合作的情况下，制造商对零售商地区性广告的分担比例都随着产品差异程度的增加而提高。说明随着同类产品间差异程度的增加，零售商地区性广告对消费者产品需求的影响会更加明显，零售商地区性促销广告对制造商产品销售来说就越发重要，制造商们在零售渠道产品销售的竞争也会更加激烈，也会加大零售商合作广告的分担比例。

(二)局限和展望

本文的研究成果使供应链合作广告理论得到了进一步完善，并为制造商在产品差异化竞争情形下与零售商进行广告合作提供了理论参考。但是本文是有局限的：只研究了存在产品差异化竞争的两个制造商与同一零售商之间的广告合作问题。展望未来的研究，从生产者角度可以拓展到多个制造商产品差异化竞争的情形，或从制造商的品牌效应对合作广告产生影响的角度进行更深入的研究。