基于岩土工程原位测试技术的桩基水平承载力分析

王 舒，段伟宏，马 冲，张 涛

(1.贵州民族大学建筑工程学院，贵州 贵阳 550025;2.山西省交通规划勘察设计院，山西 太原 030012;3.中国地质大学(武汉)数学与物理学院，湖北 武汉 430074;4.中国地质大学(武汉) 工程学院，湖北 武汉 430074)

近年来，伴随着国民经济的飞速发展和基础设施的不断完善，大型基础设施和高层建筑不断增加,这些建筑设施对其基础承载力均有着较高的要求，天然基础通常难以满足设计要求，需要进行不同方式的地基处理。桩基础(也称桩基)是高层建筑常用的一种深基础形式，具有稳定性好、承载力高和适应多种复杂地质条件等优点,同时桩身刚度相对较大，可将外部荷载集中传递至坚硬土层或岩层等持力层中，有效地减小了建(构)筑物基础荷载扩散分布引起的不均匀沉降[1-3]。常见的工业和民用建筑桩基础中，主要考虑桩基的竖向承载力，国内外学者对此已进行了系统研究，并取得了大量成果[4-7]。目前评价桩基竖向承载力的方法主要有：静载荷试验法、标准贯入试验法、高应变动测法和静力触探法等[8-9]。

在港口码头、桥梁抗震等工程建设中，桩基础不仅承受上部结构传递来的竖向荷载，还会受到波浪、大风和船舶撞击等引起的水平荷载。桩基的水平承载特性对于结构的稳定性和安全服役寿命有着至关重要的影响，因此需要对桩基在水平荷载下的受力形状进行深入的研究。桩基水平承载特性研究的主要内容是桩与桩侧土体之间的相互作用规律。国内外学者主要从理论解析、模型试验和数值模拟三个方面入手，获得桩基水平承载力的理论解答和预测模型。如McClelland等[10]于1956年首次提出了水平受荷条件下桩-土间相互作用的p-y曲线，并利用该曲线分析了桩体的受力特性和桩周土的应力状态；Douglas等[11]提出采用弹性理论方法分析水平受荷桩的桩-土间相互作用；此后，Poulos等[12]通过桩-土间相互作用的p-y曲线研究了土体应力状态对桩身弹性模量的影响，并在弹性理论法的基础上，综合了该曲线的优势，提出了一种研究桩-土间相互作用的耦合算法。天然土体具有复杂的物理力学性质，其沉积环境也千差万别，理论分析方法难以反映桩-土间相互作用的真实情况，数值模拟方法可以较好地解决这一问题。如Yang等[13]系统研究了成层地基对水平受荷桩桩身弯矩、剪力和土抗力的影响规律，揭示了不同成层条件下桩-土间相互作用的p-y曲线的特点，所得的桩基水平承载力预测值与实测值的误差在20%范围内，具有较高的精度。模型试验是研究桩基水平承载特性非常有效的方法之一。如Lee等[14]在标定罐中模拟砂土层状地基，进行了模型桩荷载试验，认为桩基水平承载力受中间土层的影响较小，受上部和下部土层的影响最大，相同水平荷载条件下，桩身弯矩转折点在单一土层和层状地基中的位置差异不明显。值得注意的是，现有关于桩基水平承载特性的研究多集中于理论分析和现场试验，但理论解析解是对理想情况的分析结果，现场试验费用较高，且应用的场地和规模都存在较大的局限性。岩土工程原位测试技术具有方便、快捷、成本低和测试结果具有较高精确度的优点，可借助此手段对桩基水平承载特性进行评价。如刘锦[15]研究认为孔压静力触探试验结果可以用来评价桩基水平承载力，并与现场静载试验结果相对比，验证了该方法对管桩和水泥搅拌桩的可行性；段伟宏等[16]通过对比3种不同的原位测试技术分析水平受荷桩的应力-应变特性以及桩基水平承载力的预测结果，结果表明孔压静力触探技术在评价桩基水平承载力方面具有较好的优势。此外，现有研究人员还在原位测试技术评价桩基水平承载力的基础上，给出了软土地基刚柔性桩水平承载位移控制标准[17-18]。

本文在上述研究的基础上，概述了桩基水平受荷的机理，并以静力触探技术为测试手段，对水平受荷桩所处土层进行测试，提出利用岩土工程原位测试结果评价桩基水平承载力的改进方法，并利用有限元分析软件，将基于岩土工程原位测试技术的桩基p-y曲线法计算结果与传统的Mallock桩基p-y曲线法计算结果进行了对比分析，以验证该评价方法的有效性。

1 桩基水平受荷机理

1. 1 桩-土之间的相互作用

水平荷载作用下，桩-土之间的相互作用主要可分为以下3个阶段：①弹性变形阶段：荷载水平较低时，在循环荷载作用下，桩周土体变形逐渐达到稳定的状态，且卸荷后土体变形基本可以恢复，此时桩的水平抗力主要由上部土体提供；②塑性变形阶段：随着荷载水平的不断增大，桩的水平位移增加量比弹性变形阶段有显著的增加，桩的水平位移随荷载循环作用次数的增加而增加，但逐次水平位移增加量呈减小趋势，表层土体发生塑性屈服变形，水平荷载作用范围向土体深处不断发展；③失稳破坏阶段：随着表层土体塑性变形的不断增大，直至失稳破坏，此时桩的水平位移骤增或挠曲变形超过允许值，无法满足设计要求[19]。

1. 2 桩基水平承载特性的影响因素

桩基水平承载特性的影响因素有很多，比如桩的直径、桩体刚度、泥面以下部分桩长、桩顶嵌固程度、桩侧土体强度以及桩身允许变形等。水平荷载下，桩的抗弯刚度对桩侧土的响应有显著的影响，可以通过桩-土相对刚度T来反映桩体刚度对水平承载力的影响，其表达式为

(1)

式中:m为反映土体水平抗力水平的比例常数(N/m4)；E为桩的弹性模量(N/m2)；I为桩截面惯性矩(m4)；b0为桩截面的计算宽度(m)。

根据桩-土相对刚度T的大小，水平受荷桩可分为刚性桩、半刚性桩和柔性桩3种类型，其中半刚性桩和柔性桩又统称为弹性桩。但根据桩顶约束形式的不同，上述3种类型桩体的受荷破坏模式不同[20]。本文给出了桩顶自由和嵌固两种约束形式下刚性桩、半刚性桩和柔性桩的破坏模式，见图1至图3。

图1 刚性桩的破坏模式Fig.1 Failure mode of rigid pile

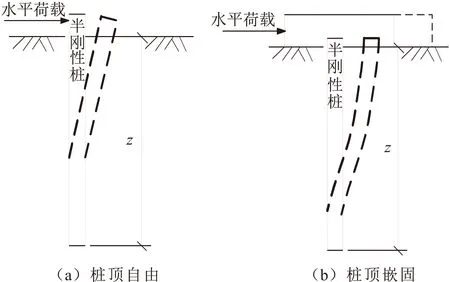
图2 半刚性桩的破坏模式Fig.2 Failure mode of semi-rigid pile

图3 柔性桩的破坏模式Fig.3 Failure mode of flexible pile

由图1至图3可见：对于刚性桩，桩顶自由时桩体绕桩底一点做刚体转动[见图1(a)]，桩顶嵌固时桩体做平动[见图1(b)]；对于柔性桩，桩身发生挠屈变形，下段桩体嵌固于土中，无法发生转动，其破坏模式与半刚性桩(见图2)类似，区别在于桩顶自由时桩体存在两个位移零点[见图3(a)]，而嵌固情况下桩体只有一个位移零点[见图3(b)]。

2 桩基水平承载力的计算方法

2.1 传统的p-y曲线法

传统的p-y曲线法，也称复合地基反力系数法，是改进的文克勒地基梁法。该方法将阻止水平受荷桩变形的桩周土简化为非线性离散分布的弹簧，桩-土间相互作用的关系通过p-y曲线来反映。图4为水平荷载作用下桩-土间典型的p-y曲线。

图4 水平荷载作用下桩-土间典型的p-y曲线[16]Fig.4 Typical p-y curves of pile under horizontal loading[16]

传统的p-y曲线法虽然假定土体为离散的非线性弹簧，但土体的工程性质通常通过现场静载试验获得，因此p-y曲线中各离散弹簧单元的相互作用已包含其中。该方法操作简单，计算结果具有较高的精度，已在工程设计中得到了广泛应用。

岩土学者Matlock[21]于1970年提出了软黏性地基中经典的p-y曲线模型，见图5。该模型将桩侧土体抗力p与桩身水平位移y之间的关系表示为

(2)

式中:pu为桩侧土体水平极限抗力(kPa)；p为桩侧单位土体抗力(kPa)，与深度z存在某种函数关系；y为桩身水平位移(mm)，是深度z的函数；y50为桩侧土体抗力达到极限值的50%时所对应的桩身水平位移(y50=2.5ε50D，其中ε50为不固结不排水三轴压缩试验时最大应力50%对应的应变，D为桩径)(mm)。其中，桩侧土体水平极限抗力pu可表示为

pu=NcsuD

(3)

式中:su为不排水抗剪强度(kPa)；Nc为承载力因子；D为桩的直径(m)。

图5 Matlock经典的p-y曲线模型[21]Fig.5 Classical p-y curve model proposed by Matlock[21]

无论黏性土还是无黏性土地基，利用传统的p-y曲线法评价桩基水平承载特性均需获得准确的计算参数，如不排水抗剪强度su等，而室内试验对试样的扰动和保存要求较高且成本高，因此岩土工程设计者们亟需一种便捷、准确获取土体参数的技术。

2.2 改进的p-y曲线法

静力触探技术是一种原位评价土体工程性质的测试技术，带有多种传感器的探头在贯入土体的过程中可以连续获取不同深度处的土体参数，且对土体的扰动较小。因此，可以考虑将静力触探技术测试获得的土体参数应用于p-y曲线模型计算中，为桩基水平承载特性的评价提供新的途径与思路。传统的p-y曲线模型中最重要的两个计算参数是pu和y50，见公式(2)。静力触探探头贯入土体过程中主要可获得的测试参数有：锥尖阻力qc、侧壁摩阻力fs和孔隙水压力u。如何将静力触探技术获得的测试参数与p-y曲线模型中的计算参数联系起来，成为建立新的计算模型的关键。

根据Matlock的桩侧土体水平极限抗力pu的计算公式(3)可知，影响土体水平极限抗力的重要参数是不排水抗剪强度su。而针对su值的静力触探解译方法主要有理论方法和经验系数法两种[22]。由于理论方法需要对土体的破坏模式、边界条件等因素进行一定的假设，且计算过程也较为复杂，实际应用时仍需现场验证，因此经验系数法更易被广泛应用和工程设计者们接受。利用锥尖阻力和孔隙水压力估算土体的不排水抗剪强度su一般采用下式：

(4)

式中:qt为经过修正的锥尖阻力(MPa)；u2为锥尖处测得的孔隙水压力(kPa)；Ne为有效圆锥系数。

经过修正的锥尖阻力qt可按下式计算：

qt=qc+u2(1-a)

(5)

式中:qc为实测的锥尖阻力(MPa)；a为探头净面积比，取值0.8。

当土层的孔隙水压力较高时(如非常软的黏土层中)，公式(4)的计算精度会受到较大的影响，此时可以采用超静孔隙水压力来估算土体的不排水抗剪强度su：

(6)

式中:u0为相应深度处的超静孔隙水压力(kPa)；NΔu为超静孔压圆锥系数。

将公式(4)、(6)分别代入公式(3)，即可得到基于静力触探技术测试得到的桩侧土体极限水平抗力pu的计算公式为

(7)

传统的p-y曲线模型中另一个重要的参数为y50，该参数可通过三轴压缩试验获得的ε50值来计算。对于黏性土层而言，其y50与ε50之间的关系可表示为

y50=2.5ε50D

(8)

Ebrahimian等[23]通过对大量的场地原位测试数据进行概率统计分析，认为采用锥尖阻力qc和超固结比OCR估算ε50值具有较高的精确度，其计算公式为

ε50=0.85qc+OCR-4.5

(9)

式中:OCR为超固结比。

选用公式(9)估算参数ε50是基于进化多元回归理论，通过均方根误差和平均绝对误差来评价预测模型的优劣。将公式(8)和公式(9)代入Matlock经典的p-y曲线关系式[见公式(2)]，可得到基于静力触探测试的桩基水平承载特性p-y曲线方程：

(10)

3 桩基水平承载特性的数值模拟

3. 1 工程概况

某高层建筑位于软土地基上，其主体部分基础采用钻孔灌注桩形式，场地前期曾进行了静力触探试验，用以初略划分土层和获得土性基本参数。该工程场地静力触探的测试结果及对应的土层划分，见图6。

图6 测试场地典型的静力触探曲线及对应的 土层划分[16]Fig.6 Typical cone penetration testing curves and soil classification[16]

由图6可见，该高层建筑基础所在地层自上而下主要有：①表层素填土，为软塑-可塑状的粉质黏土，局部含有植物根茎，土层物理力学性质不均匀，易于压缩，不可作为建筑物持力层；②淤泥质粉质黏土，呈流塑状态，土层压缩性很高、强度低；③粉细砂，级配不良且呈中密状态，土层压缩性、强度中等，不宜作为建筑物持力层；④粉质黏土、淤泥质粉质黏土，软塑-可塑状，土层中等压缩性、抗剪强度偏低，一般不宜作为建筑物持力层。粉质黏土(约30 m深度处)以下多为细砂层，该层细砂密实且饱和，级配不良，局部夹杂有淤泥质粉质黏土，具有较高的强度和较低的压缩性，可选作上部建筑物的持力层。

3. 2 模型的建立

Abaqus有限元计算软件功能强大、全面，通过装配几何模型、设置荷载与边界条件、网格划分、分析计算和后处理等步骤，可实现岩土工程中许多复杂问题的数值模拟计算与分析。水平受荷桩的变形与桩-土间的相互作用是一个复杂的受力及变形过程，本文采用该有限元分析软件对桩体的水平承载特性进行数值模拟计算与分析。

本次选取两根钻孔灌注桩A、B的桩长为35 m，直径为1.2 m，桩身混凝土为C35，内部嵌入螺纹钢筋(HRB335)。计算模型对钢筋材料进行了简化，仅嵌入了主筋而未设置箍筋，沿桩身20 m以上每1 m建立一个截面，桩身20 m以下每5 m建立一个截面，用来输出桩身截面弯矩；桩侧土体沿桩径方向取10倍的桩径长度，深度取40 m，其中桩侧部分取35 m的深度，桩底以下取5 m的深度，根据现场试验中的场地土层分布，为了简化模型将桩侧土体分为6层；桩身采用线弹性模型，钢筋为理想的弹塑性模型，根据现场试验桩基的具体情况，混凝土和钢筋的材料参数见表1。为了方便对土体材料参数进行取值计算，有限元模拟中采用线弹性模型和Mohr-Coulomb模型作为土体材料本构模型，其模型参数见表2。

表1 钻孔灌注桩材料参数

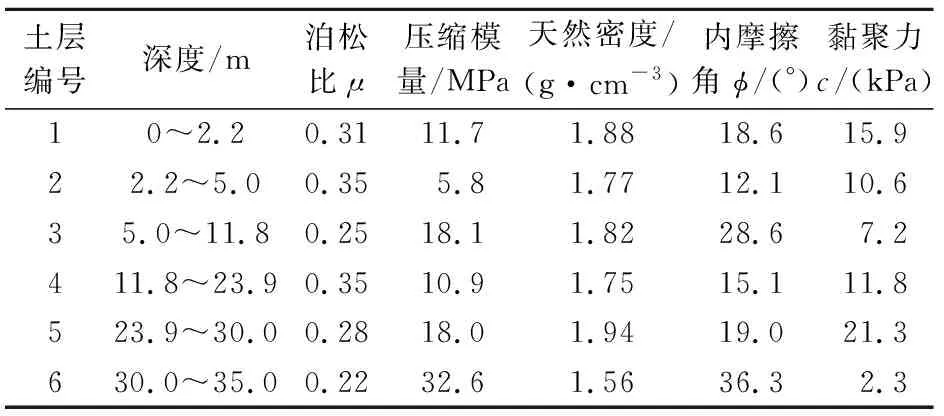
表2 土体本构模型的参数

本次模拟中桩土法向的接触模型采用硬接触和默认值，切向模型采用罚函数。桩-土界面间的摩擦角δ是影响水平承载性能的关键因素，可以通过土体内摩擦角φ计算桩-土界面的摩擦角。为了简化方便，模型中桩-土接触面之间的摩擦系数统一取0.3。分别对土体和桩施加初始地应力，对于有多层土且土体本构模型参数不同的情况下，可以对每个土层的上下边界进行设置，边界内部深度处根据上下边界土层进行插值。对于两根钻孔灌注桩，分别采用增量为41 kN和30 kN两种情况进行模拟。桩-土模型需要在土体底面和侧面设置约束条件，以免出现刚体位移，导致计算不收敛。土体底面采用固定支座以限制底面各方向的平移和转动，土体侧面需要约束水平面上的运动，这与实际工况条件非常接近，以保证模型计算的稳定性以及计算结果的可靠性。模型中桩和土体均采用三维八节点单元，配筋采用二维线性单元。实体单元采用线性减缩积分单元的方法，位移要求精确度高，网格扭曲变形分析精度不会受到较大的影响，而且荷载较大时不会出现剪切自锁。

3. 3 数值模拟计算结果与对比分析

本文利用Abaqus有限元软件，可模拟计算得到水平荷载初始增量分别为41 kN和30 kN时灌注桩A、B在各级水平荷载作用下桩身水平位移(y)、桩身截面弯矩(M)以及桩侧土体抗力(p)随深度的变化曲线，详见图7、图8和图9。

图7 灌注桩A、B在各级水平荷载作用下桩身水平位移随深度的变化曲线Fig.7 Curves of horizontal displacement of pile body of pile A and B under horizontal loading with different soil depths

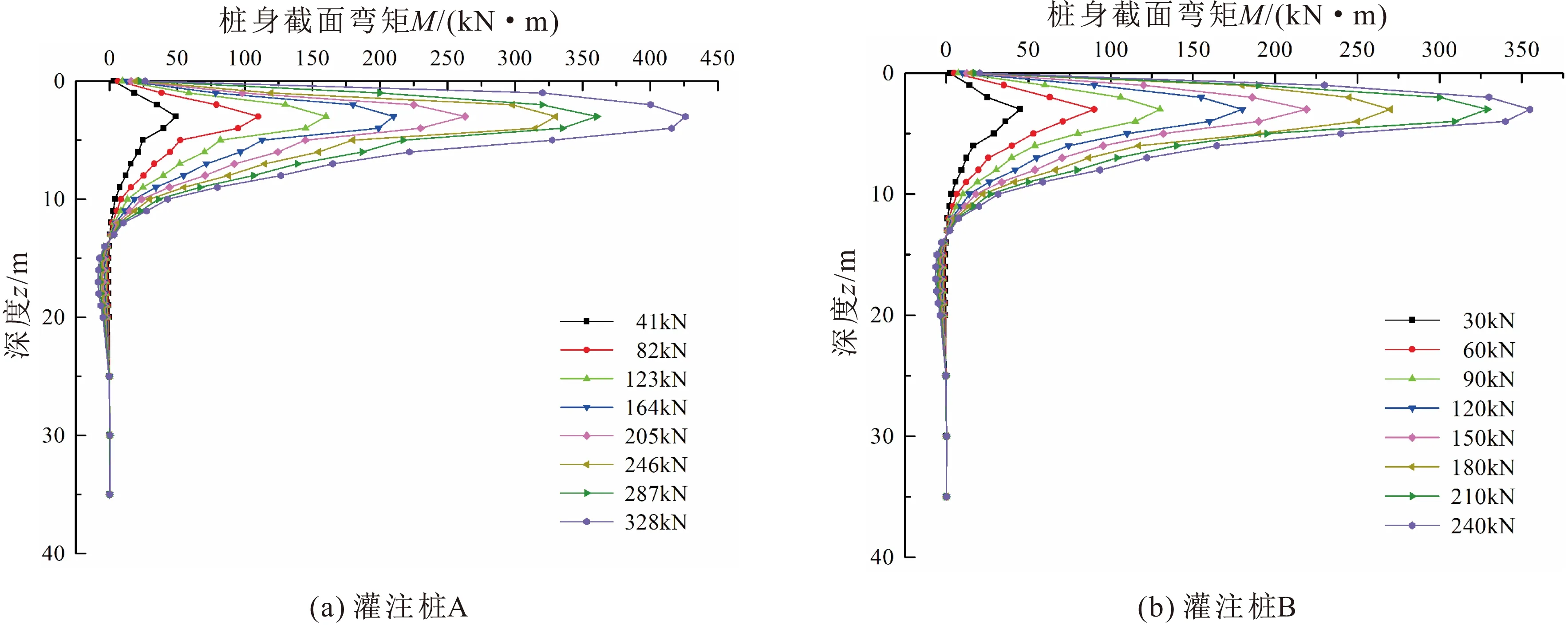
图8 灌注桩A、B在各级水平荷载作用下桩身截面弯矩随深度的变化曲线Fig.8 Curves of bending moment of pile body section of pile A and B under horizontal loading with different soil depths

由图7可见，桩身水平变形随深度增加而减小，其显著变形集中在14.5 m以上的部分，且在7.5 m附近出现反弯点；随着荷载水平的提高，桩身水平变形增量逐渐增大，灌注桩A在水平荷载达到287 kN、灌注桩B在水平荷载达到180 kN时桩身水平变形出现显著的增加。

由图8可见，桩身截面弯矩集中分布在14.8 m以上的部分，其随深度增加先增大后减小，深度进一步增加后出现反弯点；随着荷载水平的提高，桩身截面弯矩逐渐增大，最大弯矩点随着荷载增大向土体深处发展。可见，桩-土间的相互作用主要发生在上部土体中，仅依靠增加桩长度的方法对提高桩的水平承载力没有显著的影响。

图9 灌注桩A、B在各级水平荷载作用下桩侧土体抗力 随深度的变化曲线Fig.9 Curves of lateral earth resistance of pile A and B under horizontal loading with different soil depths

由图9可见，桩侧土体水平抗力随深度的变化趋势与桩身截面弯矩的变化趋势基本相同，即表现为桩侧土体水平抗力随深度的增加先增大后减小。

根据上述各级水平荷载下桩侧土体抗力与桩身水平位移的数值模拟计算结果，可以得到桩侧土体抗力随桩身水平位移的变化趋势，将地面以下2 m、3 m、5 m、8 m处的桩侧土体抗力与桩身水平位移的关系曲线数值模拟计算结果与本文中基于静力触探测试的p-y曲线法的计算结果进行了对比，详见图10。

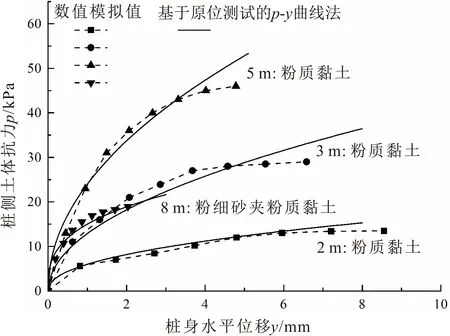
图10 数值模拟与基于原位测试的p-y曲线法计算 结果对比Fig.10 Comparison results between numerical simulation and calculation results of p-y curve based on in-situ test

由图10可见，本文提出的基于静力触探测试p-y曲线法的计算结果与数值模拟计算结果具有较好的一致性;2 m、3 m、5 m均为粉质黏土层，同一层土随着深度的增加桩侧土体抵抗变形的能力增加，这与实际情况相符。两种模型的计算结果对比分析表明，本文提出的基于静力触探测试p-y曲线法能够较好地对水平荷载作用下桩-土间的相互作用进行预测与评价。

4 结 论

(1) 桩基的水平承载特性受众多因素影响，准确评价桩基的水平承载力对于上部建(构)筑物的稳定性有着重要意义。传统的p-y曲线法虽然可较好地描述桩-土间的相互作用，但对土性参数的测试要求较高，存在成本高的局限性。

(2) 岩土工程原位测试技术在较小扰动土体的条件下，可连续、准确地获得土体的多项工程性质参数。本文提出的基于岩土工程原位测试技术的p-y曲线法可较好地描述桩-土间的相互作用。

(3) 有限元计算结果表明：不同土层深度处，基于岩土工程原位测试技术的p-y曲线法计算得到的桩身水平位移、桩身截面弯矩和桩侧土体抗力与传统Matlock的p-y曲线法的计算值吻合较好，表明本文所提出的桩基水平承载特性评价新方法具有较高的精度和良好的适用性，可为桩基承载特性的研究提供新思路。