浅析勾股定理在生活中的应用研究

周飞玲

【摘要】勾股定理源于生活，它揭示了直角三角形三边之间的数量关系，利用数形结合的方法，将勾股定理应用到我们实际生活中，解决实际问题.

一、引 言

从古至今人们对勾股定理的证明趋之若鹜，勾股定理就像几何学中的明珠，距考查勾股定理已有近四千年的历史，现约有500多种证明方法.勾股定理可以家喻户晓不只是因为证明方法多，历史悠久，更重要的是因为它在实际生活中的应用.勾股定理源于生活，贴近现实，不但揭示了直角三角形三边之间的数量关系，把数与形结合起来，而且可以解决很多与实际生活紧密联系的问题.

勾股定理的悠久历史和在我们现实生活中的广泛应用给我们带来了诸多好处.古籍《路史后记十二注》就有记载：“禹治洪水决流江河，望山川之形，定高下之势，除滔天之灾，使注东海，无漫溺之患，此勾股之所系生也.”这段话的意思是说：大禹为了治理洪水，使不决流江河，根据地势高低，决定水流走向，因势利导，使洪水注入海中，不再有大水漫溺的灾害，是应用勾股定理的结果.勾股定理在我们生活中有着很广泛的应用，例如，农村房屋的屋顶构.在物理的力学中木工等都有着广泛的应用.勾股定理的广泛应用给工程技术人员带来了便利，与我们的生活息息相关.

二、勾股定理在生活中的应用

勾股定理是几何学中的明珠，引文它的简单、实用性吸引了无数人来论证.在国外勾股定理又叫毕氏定理，是由古希腊数学家毕达哥拉斯论证的.勾股定理是在平面上的一个直角三角形中，两个直角边长的平方加起来等于斜边长的平方.如果设直角三角形的两条直角边长分别是a和b，斜边长是c，那么可以用数学语言表达：a2+b2=c2.

勾股定理是余弦定理的一个特例[1].

1.工程技术人员建造房屋时对屋顶的构造就是用的勾股定理来计算的，设计工程图纸，求圆与三

角形有关数据时都会用到勾股定理.

例如，建筑工地上有一根2.5米长钢管AB，准备斜支撑一竖直的墙OA，预支撑时钢管一端B点到墙底端O的距离为0.7米，如果钢管另一顶端A沿墙下滑0.4米，那么钢管B将向外移多少米？

解 由题意，在Rt△AOB中，

AB=2.5米，BO=0.7米.

由勾股定理得AO=2.52-0.72=2.4（米），

∴CO=AO-AC=2.4-0.4=2（米）.

在Rt△COD中，CD=2.5米，CO=2米.

由勾股定理得OD=2.52-22=1.5（米），

∴BD=OD-OB=1.5-0.7=0.8（米）.

答：钢管B将向外移0.8米.

2.物理上也有广泛应用，例如，求行走的距离、几个力的合力、物体运动的合速度，运动方向的判别……古代人们对勾股定理的应用主要体现在修建房屋、修井、造车等方面，与人们的生活和生产相关.例如，家装时，工人为了判断一个墙角是否是标准直角，可以分别在墙角向两个墙面量出30 cm，40 cm并标记一个点，然后量这两点间距离是否为50 cm.如果超出一定误差，则说明墙角不是直角.建筑工地的工程队验收工程时，为了检测某建筑物四边形地基的四个墙角是否是直角，分别测量了地基的两边长和一条对角线的长，将得到的数据进行勾股定理的验证，来检查工程是否合格.

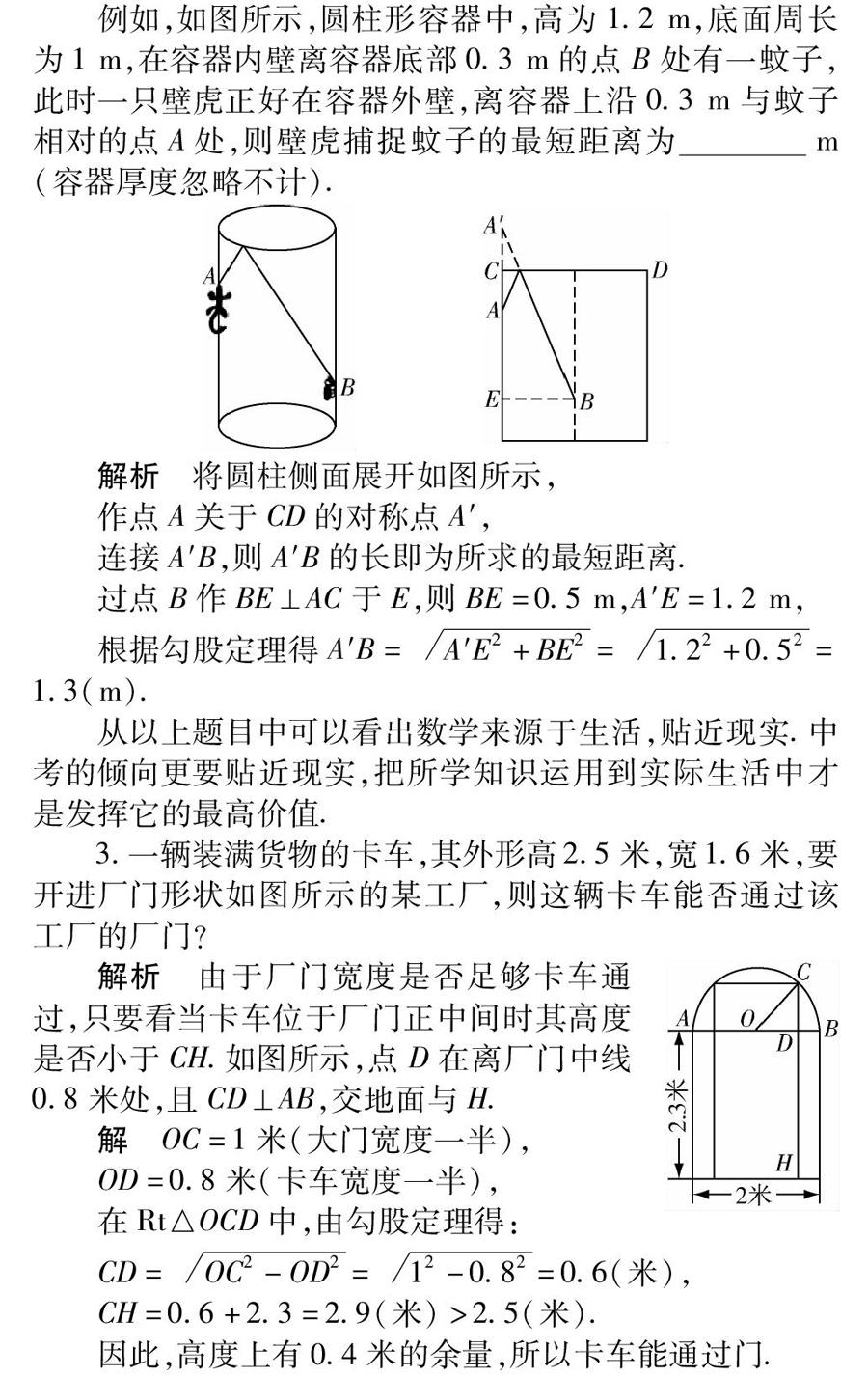
例如，如图所示，圆柱形容器中，高为1.2 m，底面周长为1 m，在容器内壁离容器底部0.3 m的点B处有一蚊子，此时一只壁虎正好在容器外壁，离容器上沿0.3 m与蚊子相对的点A处，则壁虎捕捉蚊子的最短距离为m（容器厚度忽略不计）.

解析 将圆柱侧面展开如图所示，

作点A关于CD的对称点A′，

连接A′B，则A′B的长即为所求的最短距離.

过点B作BE⊥AC于E，则BE=0.5 m，A′E=1.2 m，

根据勾股定理得A′B=A′E2+BE2=1.22+0.52=1.3（m）.

从以上题目中可以看出数学来源于生活，贴近现实.中考的倾向更要贴近现实，把所学知识运用到实际生活中才是发挥它的最高价值.

3.一辆装满货物的卡车，其外形高2.5米，宽1.6米，要开进厂门形状如图所示的某工厂，则这辆卡车能否通过该工厂的厂门？

解析 由于厂门宽度是否足够卡车通过，只要看当卡车位于厂门正中间时其高度是否小于CH.如图所示，点D在离厂门中线0.8米处，且CD⊥AB，交地面与H.

解 OC=1米（大门宽度一半），

OD=0.8米（卡车宽度一半），

在Rt△OCD中，由勾股定理得：

CD=OC2-OD2=12-0.82=0.6（米），

CH=0.6+2.3=2.9（米）>2.5（米）.

因此，高度上有0.4米的余量，所以卡车能通过门.

三、结 语

古今中外人们对数学的探究，对勾股定理的论证充分地说明了数学源于生活，服务于生活.勾股定理的魅力在就在于此.在生活中的实用性，解决生活中的实际问题，不仅在数学中用到勾股定理，物理、建筑工程等都在使用.

【参考文献】

[1]黄家礼.几何明珠[M].北京：科学普及出版社，1997.