颗粒流法在无底柱分段崩落法结构参数优化中的应用

张海峰,池秀文

(1．中国科学院武汉岩土力学研究所, 湖北 武汉 430071;2．武汉理工大学 资源与环境工程学院, 湖北 武汉 430071)

0 前 言

无底柱分段崩落法是目前国内外地下金属矿山广泛采用的一种采矿方法,产生于20世纪50年代,具有结构简单、生产效率高、机械化程度高、安全性好、采矿成本低等优势,同时也具有矿石回收率低、贫化严重等缺点。为了解决这一问题,国内外诸多学者从采矿工艺和结构参数等角度进行了大量的研究工作,获得了很多有益的成果,从而指导了无底柱分段崩落法的工程应用[1-5]。研究结果表明,加大无底柱分段崩落法的结构参数,具有减少采准工程量、降低采矿成本的优势,可实现采矿作业的集中化,提高采矿效率。但这些研究多针对金属矿山,金刚石矿山的采场结构参数优化鲜见报道。

本文以我国某金刚石矿为研究背景,该矿矿石颗粒较小,一般为零点几到1 ct,多为工业用钻。矿山＋160 m以上矿体采用露天开采,目前已经开采完毕,开始转入地下开采。因钻石多为工业用途,商业价值不如首饰钻高,因此设计采用无底柱分段崩落法进行回采,增加生产效率,提高产量。为了更多地回收矿石、减少废石混入、降低生产成本,采用颗粒流法对该矿山无底柱分段崩落法端部放矿进行模拟,设计了9组试验方案,对采场结构参数进行优化,以期提高矿石回收率、减少废石混入。

1 工程概况

该金刚石矿矿体从地表向下延伸至200 m(＋60 m中段),岩管水平断面均为似椭圆形,地表长轴约100 m,短轴约50 m,向下至＋110 m、＋60 m中段其长轴为70~75 m,而短轴为30~35 m。长轴方向约为300°,倾角约85°,倾向不定。总体形态为管状,向深部延深时管状由大变小,垂深200 m处岩管的水平断面呈弯曲的膝盖形状。岩管的围岩为片麻岩,稳固性较好。围岩蚀变为蛇纹石化,次之为片麻岩中斜长石红长石化。岩管所含的矿石类型可分为斑状金伯利岩矿石、细粒金伯利岩矿石、含围岩角砾的金伯利岩矿石、蛇纹石化碎裂岩矿石、有金伯利岩物质贯入的片麻岩矿石等5种,其中金刚石品位最好的是斑状金伯利岩。

该金刚石矿采用露天方法开采上部矿体,开采深度为100 m(＋260~＋160 m),采用汽车螺旋运输方案,当露天坑采至＋160 m水平时,由于采坑底面积的限制,无法准备出新的开采水平,上部露天开采已结束,再向下延伸很困难,因此,需要进行露天转地下开采工作,以保证矿山的正常运转与不停产过渡。综合考虑该矿矿床赋存环境、矿床地质、矿区水文地质、工程地质条件等因素,设计采用无底柱分段崩落法、双斜井侧翼对角式开拓方案开采地下＋160~-40 m矿体,阶段高度50 m,分段高度10 m。

2 端部放矿模型与试验方案

2．1 放矿模型

构建数值模型时,如果完全参照矿体真实边界建模,虽然可以最大限度地减少误差,但计算模型太大,将会使得运算时间非常长;计算模型太小,则计算结果容易与现实情况相背离,无法应用于实际生产,因此,必须从既能满足实际问题的计算分析又能节约运行时间这一角度出发进行模型的构建。在采用无底柱分段崩落采矿法的矿山中,实践与理论研究表明,上下分段的回采进路按菱形方式布置可使得废石出现得晚,纯矿石回收率大,贫化小,放矿效果好。东北大学的刘兴国、四川建材学院的张志贵等人研究发现[6-9],前3个分段的回收指标差异较大,自第四分段开始,矿石回收指标将趋于一致,因此,从简化计算模型和符合实际应用的角度出发,不对第四分段及以下分段进行研究,只研究前三分段的矿岩移动规律,初步设计第一分段3条进路、第二分段2条进路、第三分段1条进路的模拟方案,第一分段为首分层,因此其上部矿岩接触面呈水平形状。由于该模型左右对称,因此只取左侧一半模型进行研究,在颗粒流方法中,设置中间对称轴的摩擦系数为0,可以实现对称模拟的目的。回采进路宽3．3 m,高2．8 m,按菱形布置,垂直进路方向和沿进路方向的模型如图1所示。

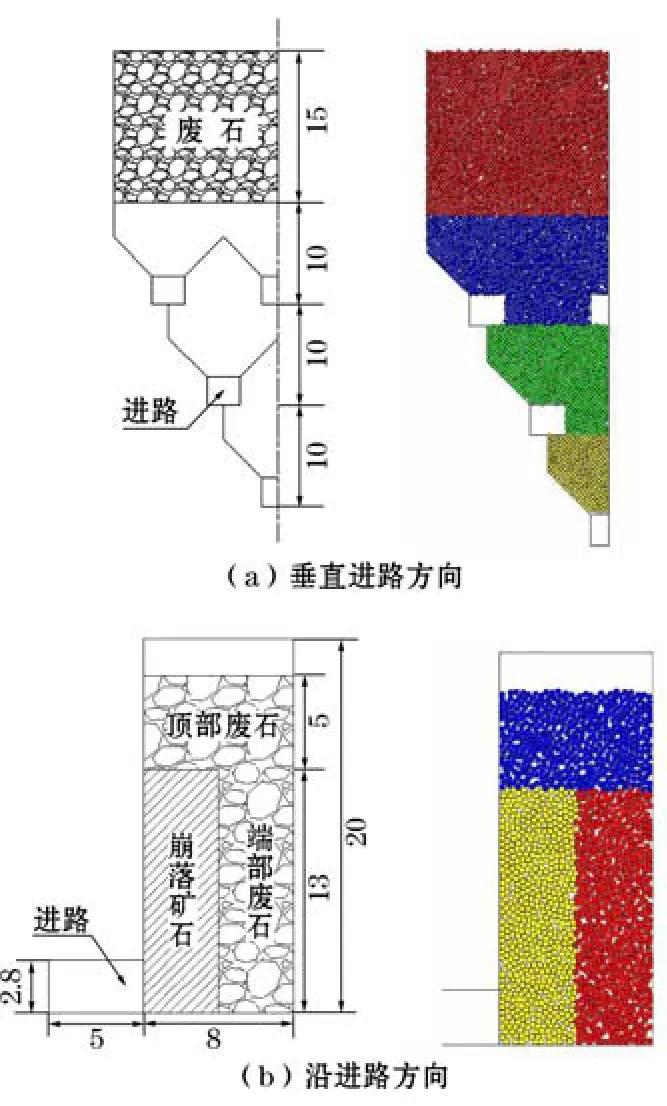
图1 计算模型示意图(单位:m)

爆破后的松散矿岩是各种不同尺寸的矿岩块集合体,各种不同块度级的重量所占总重量的百分比,称为块度组成。不同的块度组成体现了崩落矿岩分布的不均匀性,通过对颗粒半径r进行Gauss赋值可模拟不同的块度组成。对恒定颗粒半径与变化的颗粒半径2种情况下的无底柱端部放矿进行了研究,结果表明二者的回收率与贫化率变化较小[10]。可据此简化数值计算,将颗粒半径r设置为恒定值,根据矿山提供的资料,确定半径r＝0．15 m。其它微观力学参数见表1。

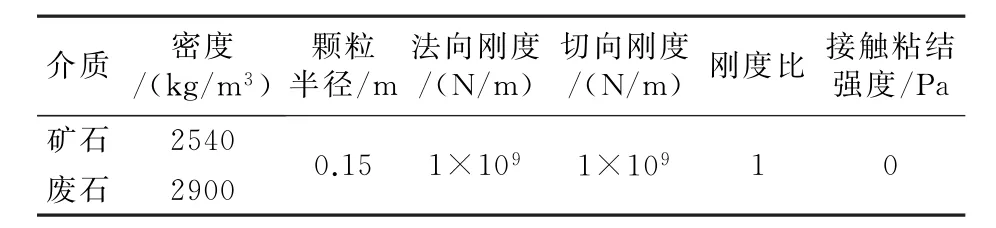
表1 计算模型微观力学参数

2．2 试验方案

截止品位仅和矿石残留体有关系,不同的截止品位所留下的矿石残留体形态大小不同,从脊部残留体体形态可以看出,不同的截止品位得出的最佳进路间距是一样的。因此,本文采用截止品位(0．205 ct/t)控制放矿,该截止品位对应于矿岩堆中的矿石与岩石体积比值1∶3。在端部放矿过程中,矿石贫化随放出量的增加而增大,在混入大量岩石之后,当当次放出矿岩体中的矿石与岩石体积比下降至截止条件1∶3时停止放矿。

为了确定10 m分段高度下的合理进路间距和放矿步距,共设计了9组试验方案进行模拟:

(1)设计进路间距分别为10,11,12 m和13 m,共计4组试验方案;

(2)最佳进路间距确定后,设计放矿步距分别为2,3,3．5,4 m和5 m,共计5组试验方案。根据试验结果得出的总矿石回收率、纯矿石回收率、贫化率(岩石混入率)和回贫差综合考虑选择最优方案。

3 模拟结果分析

3．1 进路间距

按照试验方案,对分段高度为10 m,进路间距10,11,12 m和13 m共4组方案进行了端部放矿模拟。进路间距与矿石总回收率、纯矿石回收率、贫化率和回贫差关系见图2。分析图2可得出以下结论:

(1)在分段高度一定的情况下,4个方案的矿石总回收率差异在5%以内,回收率差异不大,其中间距11 m方案回收率最高,为91．18%,相应的纯矿石回收率也最大,为66．15%。

(2)4个方案的贫化率处于13．83%~17．61%之间,差异在4%之内。其中,间距11 m方案的贫化率最低,为13．83%。

(3)回贫差指的是矿石回收率与贫化率之差,它是衡量采矿方法效果优劣的重要指标,回贫差越大经济效果越好。从图2可以看出,间距11 m方案的回贫差最大,为77．36%,放矿效果最好。

(4)进路间距11 m时,矿石总回收率和纯矿石回收率最高,贫化率最低,因此放矿的效果最好,主要原因是因为放出体在空间上与矿石堆体形态最大程度的吻合,相邻放出体相切,使得每个放矿口只回收担负的崩落矿石和上分段的矿石残留体。在10 m分段高度下,对于间距13 m的这类大间距方案,由于松动椭球体和放出漏斗不相交,相互不影响,导致放矿一开始,崩落矿岩面就产生弯曲下降,进路间的脊部残留量过大,将造成损失过大,回收率也相应地降低。间距10 m时,放出相邻的椭球体相交,与其它方案相比,由于放出漏斗流轴距离最近,相邻放出的漏斗母线交点即贫化开始时的高度最高,废石混入最早,出矿工作也是最早停止。

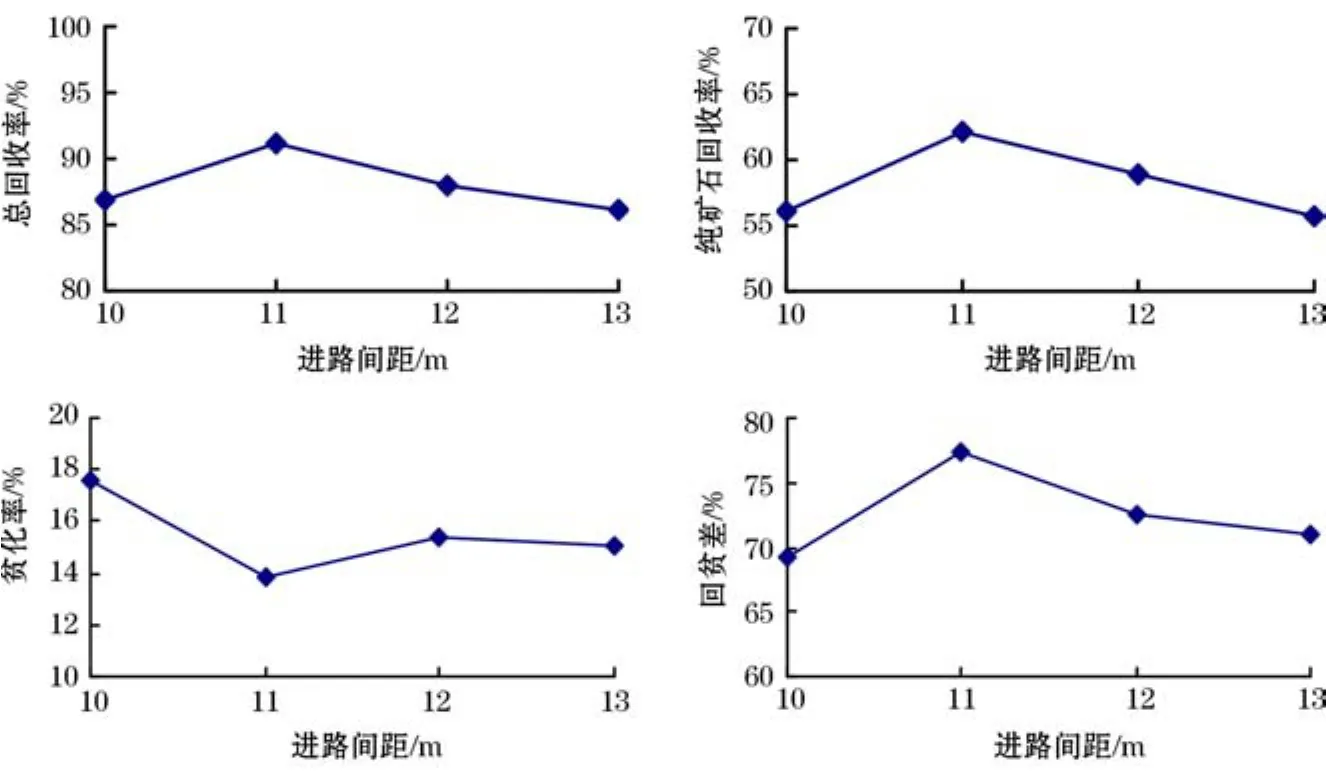
图2 进路间距与矿石总回收率、纯矿石回收率、贫化率和回贫差关系

综合以上分析可知,在一定的分段高度下,进路间距必须与放出椭球体形态相适应,间距过小或过大均会对矿石的回收指标有一定的影响。从模拟结果可知,当分段高度为10 m时,11 m为最佳进路间距。图3为进路间距11 m时的各分段放矿终了图。

图3 进路间距11 m时的各分段放矿终了图

3．2 放矿步距

按照试验方案,在分段高度10 m、进路间距11 m时,对放矿步距2,3,3．5,4 m和5 m共5组方案进行了模拟,试验结果见图3。由图3可知:

(1)分段高度和进路间距不变时,矿石总回收率曲线呈现先上升后下降的趋势,并在步距3．5 m处最大,回收率为94．15%。在放矿步距2~4 m范围内,随着步距的增加,纯矿石回收率大幅度上升,岩石混入率显著下降,步距5 m时的纯矿石回收率较4 m时略有下降、贫化率也略有升高。

(2)放矿步距4 m方案的回贫差最大,为82．16%,放矿效果最佳;步距3．5 m方案的回贫差次之,为79．04%;步距2 m方案的放矿效果最差。

(3)在固定的分段高度和进路间距条件下,放矿步距为2 m的此类小步距放矿时,由于竖向矿石层较薄,在矿石和覆盖岩石的流动性相差不大时,端部岩石将较早地混入并产生贫化,并有可能将崩落矿石拦腰截断,使得靠近端壁的矿石难以放出,从而产生贴壁残留体,造成矿石的大量损失,因此,小步距放矿时,总矿石和纯矿石回收率较低、贫化率较高,放矿效果不好。当放矿步距增大至5 m时,由于一次崩矿量大,巷道底板上靠近出矿口处的矿石将被压实形成一定的静止角,此处的矿石将很难被放出,其上的矿石沿着此处流动,在5个方案中端部残留最大,矿石的损失也因此而显著增加,同时,顶部的废石将较快地到达出矿口,造成矿石大量贫化。小步距放矿时的矿石贫化主要为端部废石的大量混入,大步距放矿时的矿石贫化则主要由于顶部废石的混入。

因此,在一定的放矿步距范围内,必然存在一个最优矿石回收指标的极值点,在该点附近,放矿效果依次变差。通过放矿步距的模拟分析可知,在分段高度10 m、进路间距11 m的前提下,最优放矿步距为4 m。图5为放矿步距4 m时的开始贫化与放矿终了图。

图4 放矿步距与矿石总回收率、纯矿石回收率、贫化率和回贫差关系

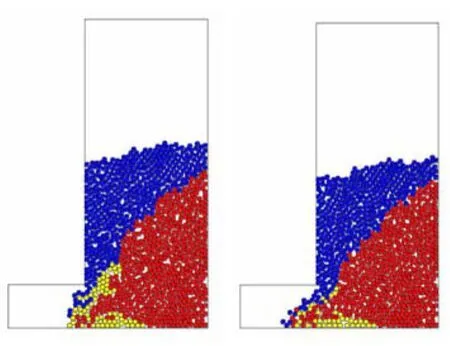
图5 放矿步距为4 m时的开始贫化和终了图

4 结 语

本文以国内某金刚石矿为研究背景,针对无底柱分段崩落法采场结构参数优化问题,采用颗粒流法建立数值模型,设计9组试验方案进行模拟分析。根据该金刚石矿山的矿岩物理力学性质,通过计算可知,在分段高度为10 m的情况下,最佳的结构参数为进路间距11 m,放矿步距4 m,可获得最优的总矿石回收率、纯矿石回收率,减少贫化率。