基于GM（1,1）的煤矿巷道围岩变形预测研究

张 勇

（同煤集团四台矿，山西 大同 037007）

在我国，由于煤炭开采深度越来越深，深部开采、开挖后围岩稳定性比较差，顶板压力大、围岩破裂、巷道位移增大、支架损坏等问题造成巷道维护变得比较困难。为了确保巷道稳定性，保障煤炭安全高效生产，分析围岩稳定性特征，并对围岩变形进行预测是非常有必要的。

影响巷道围岩稳定性的因素很多，如矿山压力、围岩类型以及支护形式等，另外还有很多很难预测和定量分析的因素，因此，巷道围岩变形预测是一个非常复杂模糊的问题，存在较大的不确定性和变化性。在预测煤矿相关内容时，灰色系统是一种非常重要的手段，很多学者也对此进行了大量的研究和分析，建立了灰色系统分析模型并进行了应用，如毕向阳等利用典型的灰色GM（1,1）系统分析了煤矿瓦斯涌出量的规律，王国军等利用灰色Verhulst模型对地下工程围岩进行了预测。

本文分析灰色GM（1,1）系统在煤矿围岩变形中的预测应用，研究其精度及误差。为巷道围岩变形提供一种较为科学、可靠的分析理论与方法。

1 巷道围岩稳定性特征

煤矿井下巷道围岩属于岩体，因此具备岩体的各类性质，如非均质性、各向异性以及非连续性等。评价煤矿井下巷道围岩稳定性的主要参数是巷道围岩塑性区大小以及围岩变形与偏移量大小。在岩体力学中，研究和计算围岩塑性区和变形与偏移量大小的方法很多。但是在煤矿井下，应用最广的仍然是观测法。通过现场观测获取最基本的数据，为理论分析提供数据依据，然后进行数值模拟与数值分析。工程实践经验表明，基于现场数据的数值模拟与分析是一种非常有效的方法。

煤矿井下围岩的特点之一就是在采掘过程中，巷道两帮与顶底板往往是煤体或者煤柱，其力学性能较差，强度往往比较低，受到多种因素作用时，容易破坏变形。这种情况对围岩控制与巷道维护非常不利，增大了工程难度。而井下围岩的另一个特点就是巷道受采动影响，围岩移近量变大会造成巷道断面变形，容易导致顶板的局部冒落、两帮的片帮以及底板的鼓底等现象发生。因此，很多矿井每年都需要投入大量的人力物力来对采区巷道进行维护，以确保巷道正常使用，保障煤炭高效安全生产。

煤矿井下巷道维护的难易程度主要取决于巷道围岩的变形量大小。巷道围岩变形量是矿山压力显现的主要表现之一，包括深部围岩变形和周边围岩变形。因此，可以把围岩变形量特别是顶板与底板的变形偏移量作为衡量围岩稳定性的重要参数，进行相关分析。巷道的围岩变形量主要受到地质因素与技术因素的作用，包括围岩力学性质、采深、采高、巷道断面积、开采顺序和位置等。

2 GM（1,1）预测模型的建立

在概率计算、回归分析的算法中，灰色系统理论的特别之处在于其克服了数学计算的局限性，解决了一直以来难以解决的连续微分方程的建模问题。灰色系统的基础理论观点就是通过原始序列的计算预测数值的边界（xmin，xmax）所围成的一个灰色平面（观点如图1所示），这个灰色平面的大小取决于预测值的区间大小，它是由已知序列向未来发展的喇叭型，指明的是预测范围。因此，在一定范围内和精度条件内，其上限与下限都是准确的预测值，当然，灰色平面的均线是最为准确的。

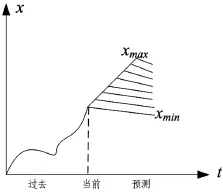
图1 灰色理论的观点示意图

2.1 GM（1,1）预测模型

通过灰色系统理论的GM(1,1)模型进行煤矿巷道围岩变形量预测，计算方法如下：

式中：

α和u为待辨识参数，序列x(1)={x(1),x(1),x(1)123,……,x(1)}是对原始离散序列x(0)={x(0),x(0),x(0)n123,……,xn(0)}进行一次累加生成处理之后的序列，即：

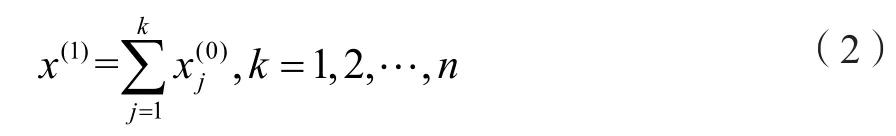
利用最小二乘法原理求得辨识参数α和u为：

微分方程（式1）的解为：

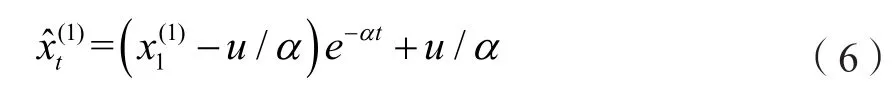
（式6）的离散响应方程为：

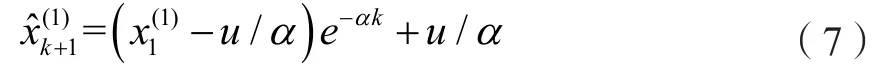
2.2 基于GM（1,1）的围岩变形预测

对大同煤矿集团公司四台矿12#层8205工作面进行围岩变形现场观测和数据采集（观测周期为30d，每隔3d进行一次测量），为了计算方便，选择5组巷道顶板与两帮变形量，具体数据如表1所示。对该数据进行GM（1,1）的预测计算。

（1）顶板变形量预测

通过表1数据建立初始序列可得：

x(0)={x1(0),x2(0),x3(0),……,xn(0)}

={25，43，85，118，168，193}

利用MATLAB进行数据计算，可得GM（1,1）灰色系统的预测结果，结果如表1所示。

同时，可得α=-0.3003和u=45.755，由此可得顶板变形量预测模型为：

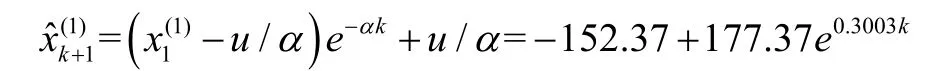
（2）两帮变形量预测

通过表1数据建立初始序列可得：

x(0)={x1(0),x2(0),x3(0),……,xn(0)}

={0，18，38，46，56，72}

利用MATLAB进行数据计算，可得GM（1,1）灰色系统的预测结果，结果如表1所示。

同时，可得α=-0.2646和u=22.2411，由此可得两帮变形量预测模型为：

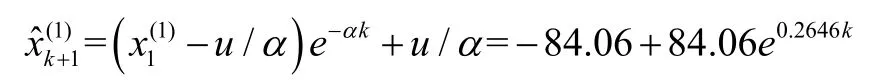
（3）变形数据分析

根据表1数据绘制实测数据与预测结果对比图，如图2所示。从图中可以看出，两者预测结果相差较小。GM（1,1）计算结果较为精确。

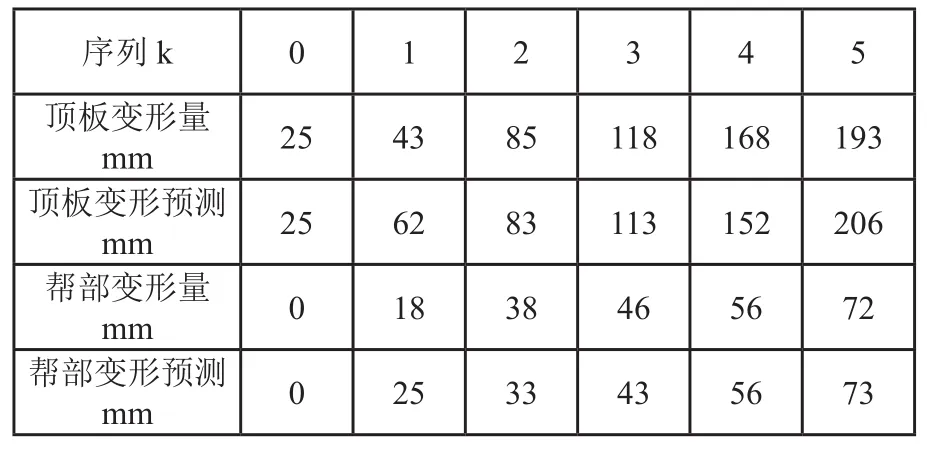
表1 实测数据与预测值结果对比

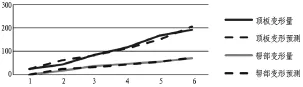
图2 原始数据与预测数据对比图

3 GM（1,1）预测模型的精度检验

c越小则模型的预测值与实际值误差就越小，模型的精度就越高，见表2。

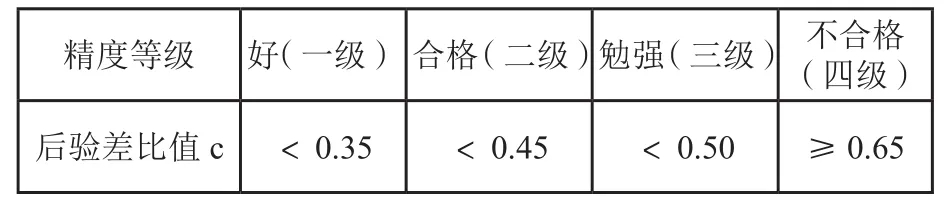
表2 精度检验参照表

（1）顶板偏移量的GM(1,1)模型精度检验

通过MA TLAB计算，残差序列εk=[0.0000，19.124，-1.116，-4.735，-15.063，13.505] ，求得残差序列和原始序列的方差并计算后验差比值c=0.1856＜0.35，因此，参照表2可知顶板偏移量预测精度为好（一级）。

（2）两帮偏移量的GM(1,1)模型精度检验

通过MA TLAB计算，残差序列εk=[0.0000，7.4609，-4.8275，-2.7803，-0.3100，1.3650] ，求得残差序列和原始序列的方差并计算后验差比值c=0.1612＜0.35，因此，参照表2可知两帮偏移量精度为好（一级）。

4 结论

（1）本文分析了煤矿井下巷道围岩稳定性特征和灰色系统基本理论，并由此建立了基于GM（1,1）灰色系统的巷道顶板、两帮偏移量预测模型。根据模型利用MATLAB进行计算，可知，顶板偏移量预测模型后验差比值为0.1856，两帮偏移量预测模型后验差比值为0.1612，即两者精度都为好。

（2）计算表明，基于GM（1,1）灰色系统的巷道顶板、两帮偏移量预测模型能够较好地进行预测，为现场开采和围岩控制提供了客观依据，具有一定的科学意义和指导意义。

（3）由于灰色系统理论具有一定的局限性，当预测序列长度太大时会逐步发散，因此，该模型可作短时间内的预测。