超精密铣削加工自由曲面光学元件误差补偿方法*
曹 义
(郑州科技学院 车辆与交通工程学院,郑州 450064)
0 引言
自由曲面光学元件是一种复杂的、无对称轴的异形曲面元件。近年来,随着自由曲面光学技术的不断发展,有效消除了高性能照明系统中对光源方向的严格要求,提高光能利用率的同时为光学元件设计者提供了很大的设计自由度[1-2]。
自由曲面光学元件的制造方法需要具备3个或多个数量的自由度。目前常用的自由曲面光学元件制造方法主要有超精密制造技术,如多轴车削、飞切、铣削以及磨削等[3-6]。然而,光学系统设计和应用对自由曲面光学元件的精度具有较为严苛的要求,工件表面粗糙度需要达到纳米甚至亚纳米级[7]。因此,在自由曲面元件加工过程中需要更好地控制和消除主要误差来源以满足加工精度要求。近年来人工误差修正方法一直应用于金刚石车削加工中刀具误差的修正,大多数精密金刚石车削机床现在也配备了机床误差测量和校正系统,但这种方法并没有应用到多轴铣削加工中[8]。
为此,本文针对多轴超精密铣削加工自由曲面光学元件提出一种误差修正方法,用于校正刀尖半径误差、径向偏移误差以及刀具不平整度误差。校正方法对两个球形工件进行切削和测量:第一个工件用于建立刀具误差模型,第二个工件模型用于验证。刀具误差模型建立和正确性验证后,该模型可用于加工任意自由曲面过程中刀位设置、刀具和切削条件等设置。最后在MATLAB软件中实现了误差修正以及生成刀具轨迹,并通过自由曲面光学元件表面对该算法进行验证。
1 铣削实验设置
加工实验在三轴联动超精密机床(Moore Nanotechnology 350 FG)上进行,其中机床最大主轴转速为10000 rpm,铣削轴转速最大为60000 rpm。切削参数主要设置为切削深度ap、步距br、进给速度vf、每齿进给量fz以及主轴转速n。具体实验装置及参数设置如图1所示。本文三轴铣削加工过程中,沿主轴方向引入固定倾角β减少金刚石铣刀刀尖点的磨损,具体可以分解为Z轴和进给速度vf方向组成的平面上投影与Z轴之间的夹角βf,以及在垂直于上述平面上投影与Z轴之间的夹角βn。另外,金刚石铣刀公称半径为Rk。
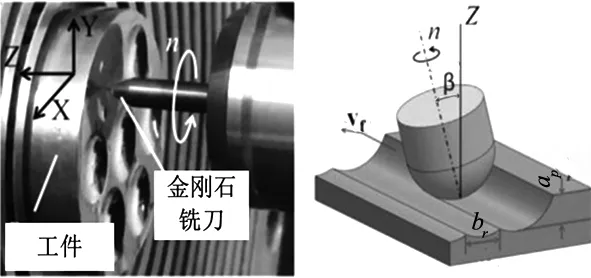
图1 实验参数示意图
1.1 切削条件设置
单槽单晶金刚石球头铣刀具体参数设置为:公称半径1.5 mm,刀具前角γ为0。工件材料为黄铜C46400,铣削过程中主轴转速n为44000 rpm。粗加工和细加工过程中Y向每齿进给量fz分别设置为9μm和1.4μm,进给速度vf设置为400 mm/min和60 mm/min,切削深度为300μm和50μm,步距br设置为100μm和20μm,固定倾角β为0。另外,进给方向上fz以及br的选择是为了生成较为理想的光学表面,不受误差矫正方法的影响。
1.2 主要误差源
自由曲面光学工件铣削加工孔径为几十毫米的光圈过程中,刀具误差是加工过程中重复误差的主要来源,对光学表面的影响较为重要。单槽单晶金刚石球头铣刀刀具误差主要包括:金刚石刀具相对于旋转轴的径向位移εr、刀尖半径误差ΔRk以及刀具前角θ的函数刀具不平整度εw(θ)。
2 加工路径规划与误差修正方法
2.1 光学系统
通常情况下,自由曲面光学系统由极坐标z=g(ρ,θ)或笛卡尔坐标z=f(x,y)定义,可能含有非球面方程,泛函基础和集,如泽尼克多项式或它们的组合。在光学设计所要求的水平上生成刀具路径需要开发自定义的刀具路径生成器,为此利用MATLAB软件开发了自定义工具路径生成器,该工具路径生成器很容易集成到下文所描述的刀具误差模型中。
2.2 刀具误差模型
根据图2建立包含主要误差源的刀具误差模型,该模型包括主要刀具误差εr、ΔRk和εw(θ)。为了确定刀具误差模型,设计合适的标准球面来匹配最终的应用程序。其中,理想的自由曲面光学元件中球面半径R和孔径RCA边缘须尽可能达到一致,如图2所示。
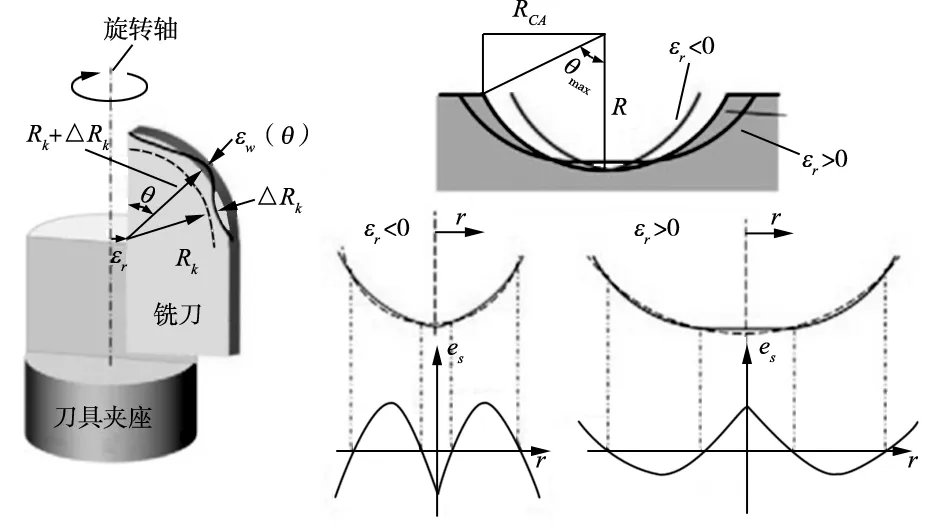
(a)刀具误差模型 (b)刀具误差曲线图2 刀具误差模型
金刚石刀具相对于旋转轴的径向位移误差εr对于光学球面的影响主要包括对于工件孔径的压缩(εr<0)和扩散(εr>0),最终导致工件表面成为非球面。被测工件与标准球面测量得到的误差值e=zm-zs就等于测量表面的高度与标准球体之间的差值,误差值e会因εr的正负呈现“M”或“W”形状的特点,如图3所示。其中,X轴零点处(r=0)相位εS表示测量数据zm;然后将改变后的数据与新的最佳拟合球面进行匹配用来获得新的zs值,直到误差值e最小。这里使用峰谷值作为测量值使误差值最小,表示为ep-v。最小峰谷值ep-v为最佳值εso对刀具误差进行估计εr=-εso。实际加工过程中,最小化误差还包括刀具不平整度和其他非零误差值。进一步,当该方法能够定量表示工件基本直径时,标准球面半径在最优值εso处和原始半径R之间的差值可以表示为ΔRk的估计值。
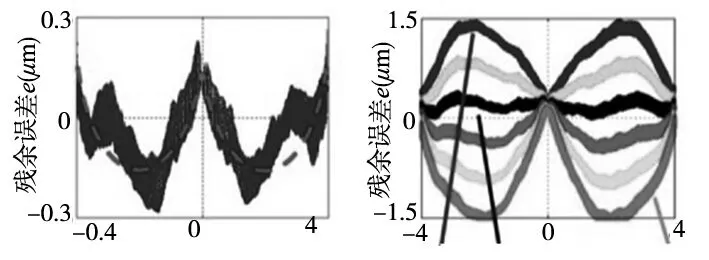
(a)径向位置r(mm) (b)径向位置r(mm)
(c)刀具角度θ(°) (d)径向位移εs(μm)图3 自由曲面具体误差类型
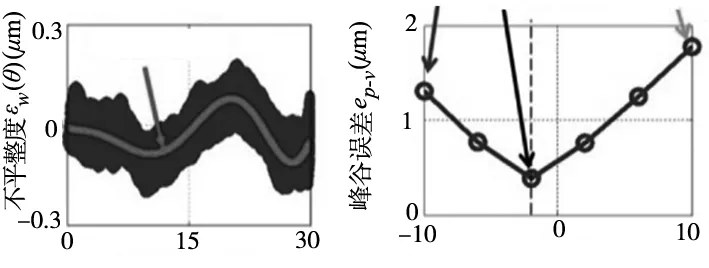
图3中最小峰谷值ep-v对应的球形工件参数为:R=8mm,RCA=4mm(θmax=30°)。利用激光干涉仪无法直接测量得到ΔRk,但可以表示出值εr。如图3a所示,工件径向截面图对误差值e进行估计,结果表示球面的径向对称误差表示为“W”形(εr>0)。干涉测量过程中实现上述最小化过程前,将误差值e与原始半径值8 mm相加。误差εS演化过程如图3b所示,图3c为刀具角度为0时峰谷值ep-v的变化曲线。由图可知,ep-v的最小值在εS=-2μm处小于400 nm。因此,球形工件的加工过程中刀具误差为εr=2μm。
εs值取最优时,工件径向对称误差的残余高度如图3d所示,此时的工件残余误差主要由刀具不平整度造成的。通常情况下刀具的不平整度εw较小,且对刀具轮廓误差的变化影响较为缓慢。因此,刀具与接触点之间的角度θ大致等于工件表面的角位置,工件表面的不平整性就会映射到刀具表面不平整度εw(θ)。由此,刀具模型误差εr,ΔRk和εw(θ)可用于加工任意自由曲面表面的刀具轨迹生成误差修正过程中。
2.3 刀具修正路径规划
为简化刀具路径,将刀具倾角β设置为0,并将自由曲面光学系统坐标系转换为笛卡尔坐标系z=f(x,y)。修正刀具轨迹生成原理如图4所示,理想曲面f(x,y)表示为灰色部分。刀具路径表示为铣刀绕旋转轴转动的半圆球,工件表面的理想切削路径由红色虚线表示。B点为理想刀具轨迹中刀具与工件表面的瞬时接触点,表示为向量rs。C点为沿局部表面法线方向en上未修正刀具法向中心位置,对应的刀具中心位置表示为rt。旋转轴通过C点在刀具轨迹A点处与刀具轨迹相交。D点为过工件表面B点平行于X-Y平面在旋转轴上的点。刀具轨迹与工件表面的接触点可以分解为向量en和ea,如图4b所示。其中,点C′和点D′分别位于直线BC和BD上。
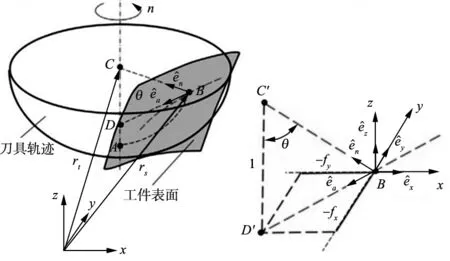
图4 修正刀具轨迹生成原理
沿切削路径上的每个B点,其工件表面法向向量表示为:
(1)
式中,fx和fy分别表示光学系统中沿X轴和Y轴的偏导数,ex,ey和ez分别表示笛卡尔法向矢量。利用刀具误差模型,刀具路径中每个点的刀具中心位置修正可以表示为:
rt=rs+(Rk+ΔRk+εr(θ))en+εrea
(2)
刀具位置修正矢量rt包括两部分:第一部分是刀具半径修正之和Rk+ΔRk以及沿en方向上刀具不平整度εw(θ)。沿刀具路径的圆截面圆弧从A点延伸到B点的刀具不平整度修正角度θ可以表示为:
(3)
第二部分为铣刀槽在D点沿旋转轴的径向偏离εr,其单位向量ea可以表示为:
(4)
当刀具倾角β固定为0时,工件表面作为刚体以角度分量-βf和-βn沿轴进行旋转,然后在刀具不倾斜的新坐标系中生成刀具路径。
3 实验验证
利用上述提出的方法对复杂自由曲面光学系统进行误差补偿过程,其中非球面项可以表示为:
(5)
3.1 标准球面测试
为验证本文所提出的误差补偿方法,对黄铜工件进行球面加工并检测。其中具体加工参数设置分别为R=8mm,RCA=8mm。加工获得的未经误差修正的球面测量结果如图5a所示。由图可知,未进行误差修正前工件表面εr和ΔRk分别为4.3μm和1.0μm,峰谷值ep-v最大值为839 nm。误差修正后测量结果如图5b所示,较为明显的是峰谷值ep-v总体误差降低到269 nm。
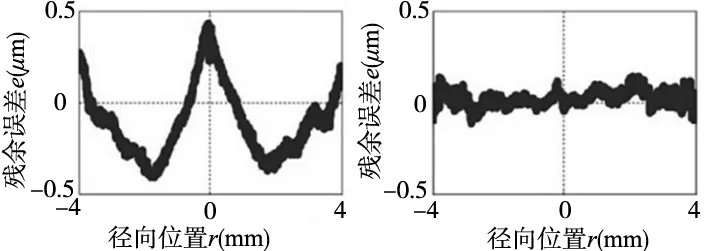
(a)ep-v=839nm (b)ep-v=269nm图5 误差修正结果
3.2 自由曲面测试结果
利用刀具误差模型,将黄铜和脆性材料加工得到式(5)描述的一般光学表面自由曲面,黄铜材料试验自由曲面如图6所示。图7a为表面轮廓仪测量图6b中沿虚线自由曲面截面表面图。图7b为测量数据zm与光学系统计算结果zp之间的误差值e=zm-zp。其中,加工黄铜材料获得的光学自由曲面峰谷误差值和残余误差分别为132nm和84nm。图7c为测量的全孔径结果,图7d对比了测量得到的峰谷误差值与计算误差值。此时,峰谷误差和残余误差值分别达到了336nm和49nm,符合工业应用领域的加工需求。

图6 加工获得的自由曲面光学表面
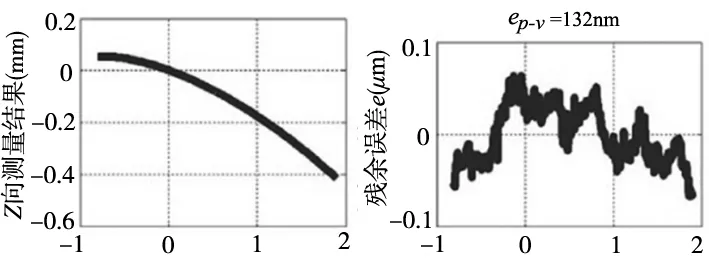
(a)Y向位置(mm) (b)Y向位置(mm)
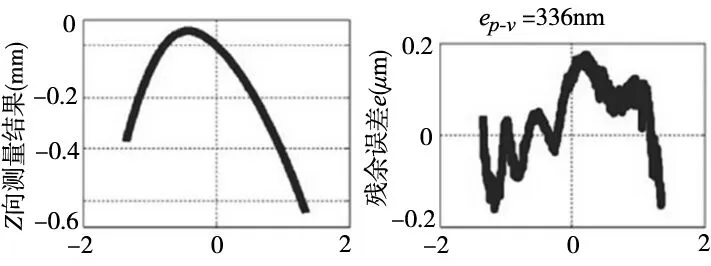
(c)Y向位置(mm) (d)Y向位置(mm)图7 自由曲面测试结果
4 结论
本文提出一种误差修正方法,用于以毫米为单位的光学孔径的误差补偿。通过标准球形工件对所建立的刀具误差模型进行验证,进而降低自由曲面光学元件加工误差。实验结果显示,自由曲面光学元件残余误差分别减少49 nm和84 nm;与测试球面相比,自由曲面峰谷误差约为570 nm。为此,基于误差补偿方法提出的刀具误差模型可进一步扩大其应用范围,减少自由曲面光学工件加工的重复误差。

