伺服速度控制参数的改进遗传算法自整定研究*
李 汐,卢少武,周凤星
(武汉科技大学 信息科学与工程学院,武汉 430081)
0 引言
永磁同步电机(PMSM, Permanent Magnet Synchronous Motor)以其结构简单,功率因数高,易于控制等优点广泛的应用于伺服系统中,而伺服系统的性能很大程度上取决于控制参数的好坏。目前伺服系统一般采用三环控制的方法[1],速度环是决定伺服系统性能好坏的关键,所以速度环控制参数好坏就直接影响到整个系统的性能。因此,对速度环的控制参数整定就显得格外重要[2]。
遗传算法是一种对种群中个体进行选择复制、交叉、变异操作从而达到寻优目的的算法[3]。现如今,遗传算法由于其寻优性能强、原理简单、易于实现等优点被越来越多的人们所使用。文献[4]提出了一种基于混合神经遗传算法(GANN)的新型预测模型,用于预测离子浮选过程中Ni(II)离子去除和脱水过程。在文献[5]中,提出了一种新的强大的自动对接方法,它可以估算柔性配体与大分子物质的联合构象,并将其与预测自由能变化的新准则函数结合起来。在文献[6]中,以跨度最小化为准则考虑了资源有限的项目调度问题, 并提出了一种新的遗传算法来解决这个问题。
传统遗传算法虽具有一定的寻优能力,但是其收敛速度慢和易陷入局部寻优的局限性让其在实际复杂的工程中应用较其他算法优势不明显。本文针对这些缺点进行改进,分别对遗传算法的初始寻优种群、选择复制算子、交叉算子,变异算子进行改进,提高算法性能并应用与伺服系统中来调节其控制参数。最后在Matlab中进行仿真实验,得到较为满意的控制结果。
1 改进遗传算法对速度环控制参数的整定
速度环的输入为指令速度,输出为电机实际转速,作为伺服系统,需要电机实际速度跟随指令速度的变化而变化。而在实际工程项目中,伺服系统速度环不仅要有良好的跟随性能,还要有一定的抗负载扰动能力和较小的超调量。对于速度环,一般采用PI控制[7-8],控制过程如图1所示。

图1 速度环PI控制过程
比例部分的作用是加快系统调节速度并减小稳态误差,但过大的比例增益会增大超调,产生过度振荡,动态性能变差甚至系统不稳定。积分部分的作用是消除静态误差,提高系统控制精度。
PI控制器的输入为误差e,输出为u,则有:
(1)
本文通过改进遗传算法来整定kp,ki两个控制参数,对于伺服系统来说,要获得满意的跟踪性能,采用误差绝对值时间积分性能作为参数选择的寻优准则函数。防止控制能量过大,加入控制输入的平方项。采用了较大的惩罚因子来避免超调[9]。最后得到的寻优准则函数如下:
(2)
其中,e(t)为系统误差,tu为上升时间,u(t)为控制器输出,ω1,ω2,ω3,ω4为权值并且ω4>>ω1。
2 改进遗传算法
2.1 对初始种群的改进
传统遗传算法的初始种群是在某范围内随机取n个点作为初始种群[10],这种方法操作简单,适用性强,但是对于多峰值的函数有较大概率取不到最值点(峰值2)附近而取在了极值点(峰值1)附近,造成算法的局部收敛,情况如图2a所示。
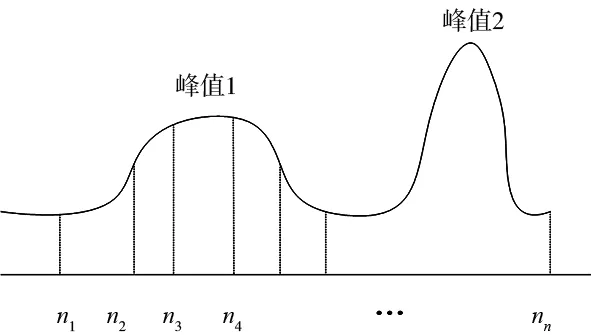
(a)传统方法的初始种群
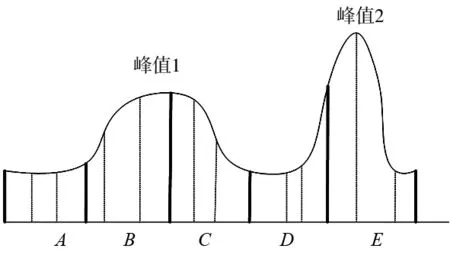
(b)改进算法的初始种群图2 传统方法与改进算法初始总群
针对上述情况,本文对初始种群的选取方法进行了改进,如图2b所示,首先将初始寻优范围分为5个区间(A、B、C、D、E),然后在每个区间内随机选取n/5个点,最后将所有选取的点组合成初始种群。这样的改进方法在保证初始种群的总体个数不变的基础上,使种群个体更加均匀的分布在寻优范围内,增加了初始种群的多样性,不仅减少了算法陷入局部收敛的概率,还使算法可以更早的收敛,提高了算法的准确性和快速性。
2.2 选择复制算子的改进
复制是从旧种群中选择出生命力强的个体来产生新种群的过程。根据达尔文进化理论,模仿了自然选择过程。根据种群个体的适配值的高低进行排序操作,然后用个体的适配值除以种群的总适配值得到个体对于种群的相对适配值:
(3)
fi是个体相对适配值,f(ai)是种群个体的适配值,n是种群的个体总数。对此相对适配值fi进行向下取整,去除相对适配值小于1的个体,在保证种群个体总数不变的情况下,根据相对适配值的大小进行复制,适配值大的产生子代多,适配值小的产生子代少。
此方法去除了适应度不高的个体,保留优良个体并复制,这种改进方法使种群整体更优良,达到了进化的目的。
2.3 交叉算子的改进
交叉运算模拟了生物进化过程中个体与个体之间的繁殖现象,个体基因与另外个体基因通过自由组合的方式得到新的子代基因。对于遗传算法来说,交叉算子对个体有基因重组的效果,有利于算法跳出局部收敛的不利情况。
传统遗传算法中任意取两个个体对其基因进行交叉,各段基因的交叉概率是固定不变的。但是随着算法的推进,种群的多样性是在逐渐减小的,如果交叉概率较小,会造成算法不能跳出局部收敛的情况,如果交叉概率较大,在算法初期就要进行较多的交叉操作,算法的收敛速度就会很慢。为此,本文对交叉概率进行了改进,提出了一种随着算法迭代次数的增加而增加的交叉概率:
(4)
Pc是交叉概率,kg是算法迭代次数。由公式(4)可以看出在算法迭代次数kg高的情况下,虽然种群的多样性低,但是交叉概率会高,有利于算法跳出局部收敛;而在算法迭代次数低的情况下,交叉概率低,交叉操作执行少,算法速度快。
对于进行交叉操作的个体,传统遗传算法是任意两个个体随机交叉,但是当两个个体非常相似的情况下交叉操作几乎是没有作用的。为了避免这种近亲繁殖的现象,本文提出了一种以两个个体的相似度大小为条件的交叉方法。对于伺服系统,其控制参数就是其个体基因,假设需要进行交叉操作的两个个体中其中一个的基因为kp1,ki1,另一个个体的基因为kp2,ki2,则两个个体的相似度值(X)为:
X=|kp1-kp2|+|ki1-ki2|
(5)
当X大于某定值的时候,说明两个个体差异较大,则进行以Pc为交叉概率的交叉操作。但是当X小于这个值的时候,说明这两个个体相似,则不进行交叉操作。对于伺服系统速度环参数,交叉运算如下:
(6)
其中,Y1,Y2为子代基因,kp1,ki1为进行交叉的其中一个个体基因,kp2,ki2为另一个个体基因。α,β为两个0~1之间的随机数。
这样的改进方法避免了相似基因的近亲繁殖,加快了算法的运行和收敛速度。
2.4 变异算子的改进
变异运算模拟了生物在自然环境中的基因突变情况,一般变异概率都很小,他能随机的改变遗传基因的值,它让单一生物衍生出多样群体变成了可能,是生物进化的动力。如果没有变异,只有选择和交叉,则算法无法在初始基因范围之外的空间范围进行收索,会使进化过程陷入局部收敛而无法跳出,影响解的质量。
本文针对变异运算中的变异概率,进行了改进。使适应度较小的个体拥有较小的变异概率,适应度较大的个体拥有较大的变异概率,这样做的原因是随着算法迭代次数的增加,种群的适应度趋近一致,种群的多样性很低,不利于算法跳出局部最优解。所以当适应度趋近于一致的时候,需要加大变异概率以跳出局部最优解,当适应度差别很大的时候减小变异概率以提升算法运行速度。改进后的变异概率如下:
(7)
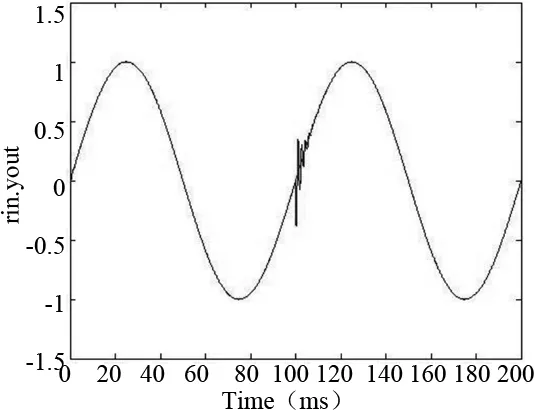
其中,fi为个体的适应度,favg为整个种群的平均适应度,Pm为变异概率,Pmax为规定的最大变异概率,Pmin为最小变异概率,fmax为个体最大适应度值。由式(7)可以看出当个体适应度fi>favg时,Pm会增大,并且相差越大Pm越大,有利于算法跳出局部寻优的情况。反之当fi (8) 其中,kp,ki为子代控制参数,kp min,ki min,kp max和ki max为控制参数的最大值和最小值,ε和θ为0~1的随机数。 为验证本文提出的改进遗传算法在伺服系统参数自整定中的应用效果相较于常规PI具有收敛速度更快,控制精度更高,抗负载能力更强等特点,设计两种方法的仿真实验,通过对比实验结果来进行对比验证。伺服电机的相关参数如表1所示。 表1 伺服电机参数 对伺服电机速度环被控对象的输入输出进行在线采样,使用递推最小二乘法(RLS)对速度环的被控对象的数学模型进行辨识,采样周期0.1ms,取准则函数的值为ω1=0.999,ω2=0.01,ω3=2,ω4=100,得到: ω(k)=ω(k-1)-0.0003478ω(k-2)+ 1.388u(k-1)+0.1984u(k-2) (9) 若电机不加负载,指令信号为阶跃信号,则采用传统PI调节和改进遗传算法的PI调节的仿真结果如图3、图4所示。 (a) 空载时传统方法控制的输入输出 (b) 空载时传统方法控制的误差图3 传统方法空载情况 (a) 空载时改进遗传算法的输入输出 (b) 空载时改进遗传算法的误差图4 改进算法空载情况 可以看出在空载情况下,传统PI调节有明显超调,而且响应速度较慢,初期波动明显,而采用改进遗传算法的情况下,无明显超调,波动较小,控制效果得到明显改善。 对于加负载的情况,采用改进遗传算法,输入指令ω*=sin(0.02πt),寻优准则的权值为ω1=0.999,ω2=0.01,ω3=2,ω4=100。经过200ms的运行时间,并且在100ms的时候对被控对象施加负载,得到结果与采用传统PI调节方法来控制的结果相比较,被控对象的数学模型为: (10) 得到如图5、图6所示的结果。 (a)传统方法控制的输入输出 (b)传统方法控制的误差图5 传统方法加负载情况 (a)改进遗传算法的输入输出 (b)改进遗传算法的误差图6 改进方法加负载情况 根据图5a、图6a可以看出,当输入正弦信号时,改进遗传算法具有很好的跟踪性能,而且在施加负载的时候,改进遗传算法所控制的系统能更好的跟随输入信号,而传统控制方法会有一点时间的明显抖动。根据图5b、图6b误差比较,可以明显的看出在施加负载的时刻传统控制方法抖动明显且持续时间较长,而改进遗传算法能更快的实现跟踪,抖动微弱。改进遗传算法在运行过程中PI参数如图7所示。 (a)参数P的变化 (b)参数I的变化图7 参数变化图 可以看出,与常规控制方法相比,改进的遗传算法具有控制精度高,收敛速度快,抗负载扰动能力强等优点,具有更好的控制效果。 本文以伺服系统中速度环作为研究对象,在传统遗传算法的基础上,对初始种群、选择算子、交叉算子、变异算子进行了针对性改进,使改进遗传算法更好的应用在伺服系统速度环的参数自整定中,并通过仿真实验进行了验证,结果表明改进遗传算法能明显改善传统控制方法的控制效果,使其控制精度提高,收敛速度加快,抗负载能力增强,达到了更好的控制效果。3 仿真实例





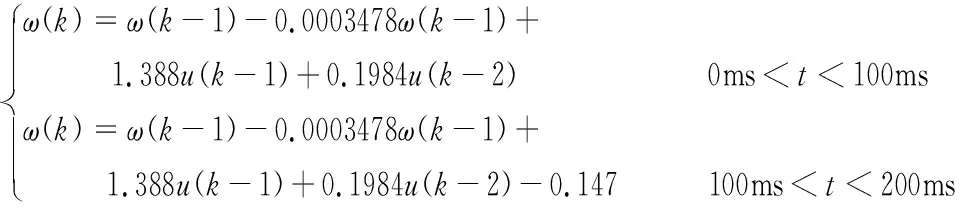





4 结束语

