基于改进的变速刀尖频率响应函数法的计算研究*

田卫军，任军学，王大振，张宝刚

(西北工业大学 现代设计与集成制造技术教育部重点实验室，西安 710072)

0 引言

铣削过程受到不确定性振动的影响是进一步提高加工性能的主要限制因素之一。不稳定性振动又称为颤振，它可能不受控制地增长，导致表面光洁度差，刀具磨损过大和刀具破损的可能，从而影响生产率。

目前为止，已经开发出来了许多颤振的预测方法，这些方法的主要结果显示了切割参数的无颤振组合的图表，称为稳定性曲线图(SLD)。特别是在叶瓣间隔开的高速下，如果选择适当的主轴转速，即可很好地利用较高的切割深度。然而，在主轴高速旋转下，每个预测模型显示的精度降低，通常不是由于分析颤振模型中引入的近似误差引起的，而是由于输入的不准确性导致。

过去的几年里，Gagnol等[1]开发了高速主轴的分析动力学模型；Cao等[2]提出了一种基于主轴FE模型的替代方法，两种模型都考虑到陀螺力矩和离心力，并强调了轴承刚度对主轴转速的依赖性；Li等[3]实现了考虑热和机械效应的综合模型，他们发现，在主轴高转速下，轴承刚度通常会降低。尽管预测方法提供了预期的结果，但仍需要一组复杂的输入参数(例如，轴承预载，刚度)来限制它们的应用。此外，这些变量也受到不确定性的影响，而且它们的辨识实验也是极具挑战性。

由于上述原因，已经开发了几种实验技术。通过冲击锤和激光多普勒振动计(LDV)或电容探头在旋转期间测量主轴动力学。Bediz等[4]开发了定制冲击激励系统，并采用两台光纤LDV自动获取微加工中的变速刀具FRF。由于对旋转主轴的影响,这种方法也存在一些安全问题，而且采集的参量也会受到相关噪声的影响。

为了全面地了解加工过程中的动力学，包括机床和加工间的相互作用，开发了基于切割操作分析的实验技术。一些研究人员将操作模态分析(OMA)原理应用于切割过程，但切割力的谐波性质仍然是其实现过程中的一大难题。为了克服这一问题，研究了基于加工具有特定形状的专用工件的测量技术。然而，由于力传感器的带宽限制和噪音的影响，限制了主轴的低转速用于刀尖FRF的识别。

本文中，实现了主轴速度提升(SSR)测试，同时有效地获得了颤振极限(即颤振频率和切割深度)，并且基于测试结果提出了FRF识别技术。然后，通过比较预测的颤振极限和实际的实验结果，在整个主轴转速范围内计算出刀尖FRF。正如本文所讨论的一样，以往的方法依赖于单个颤振条件(即噪声的高灵敏度以及所获得的实验值的误差)来评估特定主轴转速下的速度相关FRF。这里还提出了一种基于实施测试的结果来识别速度变化刀尖FRF的方法，即以更鲁棒的方式来进行识别。

1 SSR测试实验

SSR理论在文献[5]中有详细介绍。一般在测试中，主轴速度不断增加，与进给速度相匹配，以保持每个齿进给数不变。测试的主要思想是通过在单次测试期间通过改变整个范围内的主轴速度来探究SLD(即固定的切割深度，变化的主轴转速)。在频域中获取和分析传感器信号，以便研究特征频率(即颤振频率)的存在，这允许在特定切割深度处来区分稳定和不稳定的主轴转速。该方法所需的时频域分析是通过Order Analysis技术实现的。该分析的主要输出方式是瀑布图或色彩图，其显示了信号随主轴转速变化的频率值。针对这些光谱中检测到的颤振频率，提取了稳定和不稳定的切割参数。

然而，可以在整个主轴转速范围内重构SLD实验，即在不同的切割深度处重复测试几次。测试很简单，可以在NC代码中编程且运行速度非常快。

2 基于GA的辨识方法

本文中，工作条件下的刀尖FRF的计算方法为：

(1)通过SSR测试实验获得轴向切割深度和颤振频率的实验值；

(2)利用轴向切割深度和颤振频率分析公式计算。

根据Budak等[6]中公式所述，这两个参数可以用式(1)和式(2)表示：

(1)

(2)

其中，

(3)

(4)

a0=ΦxxΦyy(axxayy-axyaxy)
a0=axxΦxx+ayyΦyy

(5)

(6)

式中，N——槽纹的数量；Κt——切向切割力系数；Κr——径向切割力和切向切割力系数比率；Φst、Φex——分别表示切削起始和退出角度；n——主轴转速；k——整个振动波(即波瓣)的正整数；Φxx、Φyy——表示为不同模态参数下的刀尖FRF。

本文中，采用文献[6]中的复杂特征值通用公式：

(7)

根据所提出的理论，alim和ωc可用于识别工具尖端FRF(ξi,ωi)的模态参数。在给定的主轴转速下，通过将切割分析后的轴向深度和颤振频率实验匹配来计算这些参数。与文献[7]一样，考虑了一些假设：

(1)具体颤振条件是由单个主导模式引起的，因此所提出的方法用于识别引起颤振的主导因素。

这些假设中，只有阻尼比和固有频率是未知数。在文献[7]中，这些未知数通过分析和实验利用轴向切削深度与两个主轴转速之间的颤振频率的等价性来解决。然而，考虑到实验结果受噪声和颤振检测误差的影响，该方法的准确性将会降低。

在这项工作中，可以采用鲁棒性更强的方法，即在几个颤振极限条件下计算阻尼比和固有频率。

如文献[8]中提出的遗传算法(GA)来计算阻尼比和固有频率，即通过对目标函数f0最小化来计算其模态参数。

3 实验验证

为了验证提出方法的准确性，使用NMV 1500 DCG Mori Seiki 5轴铣床进行了一些实验测试。进行了不同切割深度的一系列SSR测试。用两个铣刀(直径8mm)Garant 201770加工了一个铝合金6082-T4合金的试样盒。该机器配备了一个发声器(Bruel & Kjaer型4165)，安装在靠近切割区的切割腔内。信号由LMS Scadas III接受，并在LMS Test.Lab软件中显示。

3.1 固定FDF的计算

在执行SSR测试之前，进行冲击试验，计算出固定条件下的刀尖FRF，并找出模态参数。

一旦确定了刀尖FRF，则采用Polymax[9]估计器来识别模态参数和模态形状，在文献[10]中也有所采用。模态参数如表1所示。基于使用复特征值的FRF公式进行模态提取(方程(7))，因此在表中显示了模式形状和模态参与因子的乘积，而不是模态刚度。

3.2 颤振极限条件的验证测试

本节中，进行了上述所提出的测试，以确定在FRF识别程序中的颤振极限条件。尤其在13000～30000rpm和0.03mm /齿进给的不同切割深度(1.0，1.5，2.0，2.5，3.0，3.5mm)进行6个开槽试验。通过指令分析获取和分析了发声器的信号。分析结果如图1，确定了以5300Hz附近的颤振频率，用于提取稳定和不稳定区。

此外，在图1中，将实验结果与通过固定FRF计算的分析SLD和文献[11]中确定的切削力系数进行比较。如图1所示，通过闲置状态下的FRF计算出的SLD仅在所研究的较低速度(约14000rpm)下才是精确的，而在叶片定位和切割深度方面都检测到了增加的差异，这些差异是由于FRF随主轴转速变化所引起的。

图1 SSR结果与分析SLD相比

4 实验结果分析

本节中，提出的FRF识别程序适用于SSR所获得的实验结果。得出了颤振频率(即约5300Hz)。由于通过实验程序(图1)获得了大量的限制条件，因此提出了基于多种条件下的鲁棒识别。

实验过程中，将主导模式被分为7组，根据叶片分布选择，在所考虑的主轴转速范围(13000～30000rpm)中，确定了7个叶片，因为它们中的每个限制条件都是集群式的。然后对不同的组执行识别算法：因此需要计算7个刀尖FRF。对于每个叶，GA可以找到能够最小化先前呈现的目标函数的最佳模态参数。因此为算法设置了600个人和10代人口。

刀尖FRF偏离空转状态；特别是提高主轴转速，固有频率降低，阻尼增加。这种行为是按照实验测试进行的，用以获取刀尖FRF，如文献[1-2,7]所述。这种趋势是由于陀螺矩和离心力导致轴承刚度降低和阻尼增加。因此，计算的变速FRF与主轴转速的物理模型一致。

表1 固定条件的模态参数

为了检查颤振预测中刀尖识别的准确性，用基于速度变化的FRF来计算SLD，并与SSR测试提取的限制条件进行比较，如图2所示。在图2中，显示了x和y方向上的刀尖FRF。并且x和y方向上的刀尖FRF被视为是相同的。

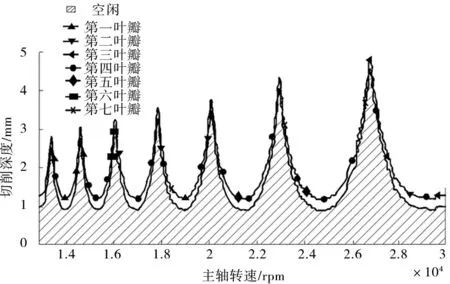
(a)主轴转速与切削深度

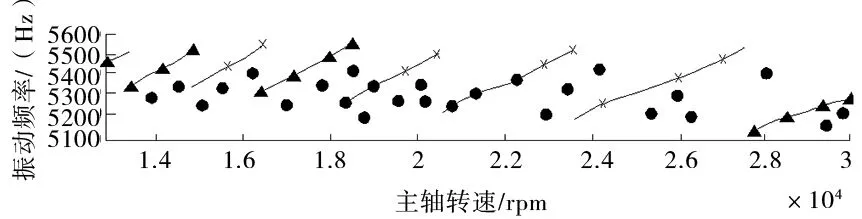
(b)主轴转速与振动频率图2 用速度变化FRF重构SLD

结果表明，在切割深度和颤振频率值方面，重建的SLD和限制条件之间存在良好的一致性，固有频率和阻尼比都随主轴转速线性变化。只有第二个波瓣(15353 rpm)的模态参数与这种趋势相比存在分歧。这可能是由于用于识别参数的条件数量很少。在测试的最高主轴转速条件下，固有频率从5375Hz的空转状态缓慢下降到约5178Hz，降低了4%。

此外，将所提出的方法与现有技术方法[12]进行比较。如前所述， Özsahin等[7]所提出的方法中由于实验振荡频率和切割深度，致使其方法依赖于单个颤振条件来提取刀尖FRF的精确性。因此，提出的方法是在单个颤振条件下进行的(总共34个)，并将结果与文献[7]提出的方法进行比较。两种方法得到的结果非常相似：固有频率和阻尼比显示出相同的趋势，随主轴转速而变化。固有频率值的差异非常小(小于0.5%)，而阻尼比的差异达到较高值。这种验证证明了在单一条件下，所提出的方法获得的结果与现有技术之间的等同性。从文献[7]的建议来看，仅仅依靠单一条件，与提出的多条件方法相比，反而出现了更复杂的结果。虽然单因素和多因素方法都导致模态参数的总体趋势相似，但多因素方法更符合物理模型的线性行为。复杂的结果是由于检测到了颤振的不准确之处。显然，如文献[7]所述，如果颤振测试重复多次，那么这些不准确性可能会降低。然而，这意味着需要更多的测试来提高该方法的准确性。SSR测试能够有效地产生大量的颤振极限条件，允许使用更精确的多条件识别技术。

5 总结

本文提出了一种运行条件下识别刀尖FRF的新方法。利用快速有效的颤振识别测试与分析稳定性解决方案相结合，以预测过程中FRF。SSR测试能够通过少量的切割运行测试出大量的实验颤振频率和轴向切割深度。通过最小化实验和分析预测极限条件之间的差异，依赖于多因素方法来计算主轴转速的动力学变化。

所提出的方法在铣削操作中得到验证，使用简单且低成本的传感器和少量的切割测试(测试时间小于30s)，就可以计算不同主轴转速下的刀尖FRF。提出的方法所得到的结果被证明符合科学文献中预期的线性趋势。提出的方法重构速度变化的SLD证明了在预测无颤振切割参数方面是准确的。