基于改进遗传算法的LuGre摩擦模型参数辨识及补偿*
李 明,封 航,李莹月
(北京航空航天大学 仪器科学与光电工程学院,北京 100191)
0 引言
伺服电机+滚珠丝杠结构构成的Z轴装配臂在做精密直线运动时,非线性摩擦力会对其精密运动的动静态特性产生较大影响,主要表现在速度跟踪时的“过零”现象和位置跟踪时的“平顶”现象,从而导致直线位置伺服运动的滑动、爬行[1]。基于非线性摩擦力数学模型,利用参数辨识来估计非线性摩擦力并对其进行补偿,可以有效地消除非线性摩擦力对直线位置伺服系统的影响。
当前,对非线性摩擦力的数学描述主要分为静态描述和动态描述[2],如Bingham模型、Stribeck模型、Dahl模型等。其中,Canudas等在1995年提出的LuGre摩擦模型解释了实际系统中观测到的Stribeck效应、Dahl效应、粘-滑运动、预滑动位移、滞后以及变静摩擦力等摩擦现象,较全面地描述了摩擦的动、静态特性[3],从而受到广泛的应用。在对LuGre摩擦模型参数进行辨识的研究方面,目前主要采用“先静态、后动态”[4-5]或“先线性、后非线性”[6-7]等两步辨识方法。此类方法实验量大,辨识过程复杂,存在求取高度非线性一阶微分摩擦模型参数最优解时易陷入局部最优等局限性。
本论文针对非线性摩擦力会对精密伺服系统动静态性能产生干扰和采用LuGre摩擦模型对非线性摩擦力进行消除过程中LuGre摩擦模型参数辨识方法复杂,以及辨识结果易陷入局部最优等问题,对非线性LuGre摩擦模型参数辨识及补偿进行了研究。在研究过程中,首先建立了Z轴直线装配臂的数学模型;然后讨论了LuGre摩擦模型下摩擦扰动对Z轴直线位置伺服系统动静态特性的影响;而后提出了一种改进遗传算法来优化摩擦参数的辨识,减小辨识结果陷入局部最优的概率,获取全局最优解;最后对LuGre摩擦模型参数进行了辨识实验,验证了所提算法的先进性;同时,在Simulink中,设计了前馈补偿器对非线性摩擦力进行了补偿。
1 Z轴装配机械臂系统描述
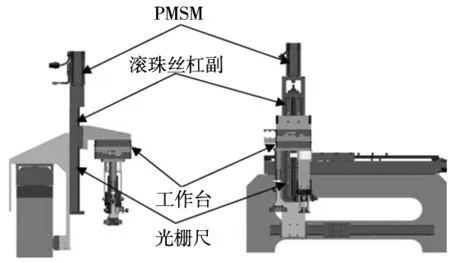
图1 Z轴装配机械臂系统结构图
Z轴装配机械臂系统结构如图1所示,该装配机械臂系统主要包括PMSM&光电编码器、滚珠丝杠副、工作台、光栅尺等。在实际工作中,由PMSM驱动工作台沿着滚珠丝杠副在Z向上做上下运动,光电编码器主要检测PMSM的转动方向和转动速度,光栅尺则实时反馈工作台实际位置。

图3 Z轴装配臂伺服系统的传递模型
1.1 PMSM数学模型
在不影响控制性能的假设条件下[8-9],建立d-q旋转坐标系下的PMSM状态方程如式(1)。
(1)
式中,R为电枢绕组电阻;ud、uq为d-q轴定子电压;id、iq为d-q轴定子电流;ψf为转子磁场等效磁链;J为转子转动惯量;B为黏滞摩擦系数;ωr为转子角速度;ω=pnωr为转子电角速度;pn为极对数。
1.2 滚珠丝杠副动力学模型
如图2为Z轴装配臂系统滚珠丝杠副的动力学模型,滚珠丝杠副的数学模型主要根据滚珠丝杠副的轴向及径向平衡来建立[10-11]。

图2 Z轴滚珠丝杠副动力学模型
根据滚珠丝杠副的轴向及径向平衡,得到滚珠丝杠副的动力学方程:
TL=K1(θr-θz)
(2)
(3)
(4)

结合PMSM的数学模型,建立Z轴装配臂伺服系统的传递模型如图3所示。
图3中,Kp、Kω为位置、速度放大器的增益,Kpf、Kωf为位置、速度反馈增益。
2 LuGre摩擦模型及摩擦扰动分析
2.1 LuGre摩擦模型
如图4所示,Canudas等[12]提出的LuGre摩擦模型在微观上将两个物体面间的接触视作由无数细小的具有弹性的鬓毛组成,当两个物体发生相对位移,接触面间的鬓毛会发生弹性形变产生回复力即为摩擦力。将鬓毛的平均弹性形变以状态变量z(t)表示,得到LuGre摩擦模型:
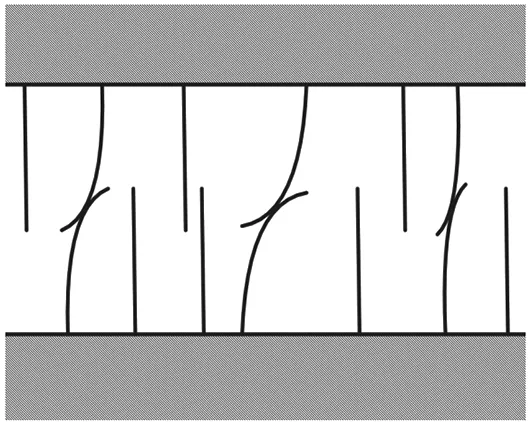
图4 LuGre摩擦模型物体接触面间微观图
(5)
式中,z(t)为鬓毛平均弹性形变;v(t)为接触面间相对速度;vs为StriBeck速度;Fc为库伦摩擦力;Fs为最大静摩擦力;σ0为刚度系数;σ1为阻尼系数;σ2为黏滞系数;Ff(t)为摩擦力。
2.2 摩擦扰动分析
根据式(5)将不可量测量鬓毛平均弹性形变当做中间状态变量,在Simulink下可建立LuGre摩擦模型的仿真模型,如图5所示。
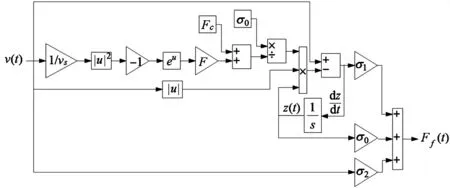
图5 LuGre摩擦仿真模型
忽略正负方向上LuGre摩擦模型参数的细微差异,设置LuGre摩擦模型的仿真参数:vs=0.0125m/s,Fc=3.82N,Fs=8.16N,σ0=84000N/m,σ1=260N·s/m,σ2=28N·s/m,得到LuGre摩擦模型静态Stribeck曲线如图6所示。

图6 LuGre摩擦模型Stribeck曲线
将LuGre摩擦模型引入到Z轴装配机械臂系统模型,设置Z轴装配机械臂系统仿真参数:R=0.01207Ω,L=2.79mH,pn=4,Mt=5kg,ψf=0.07645Wb ,J=0.0192kg·m2,Jm=0.05kg·m2,K1=1.96×106N/m,K2=9.8×104N/m,l=0.02m,cb=0.0005N/(m/s),B=0.0001N/(m/s),得Z轴装配机械臂速度和位置跟踪曲线,如图7、图8所示。

图7 速度跟随曲线
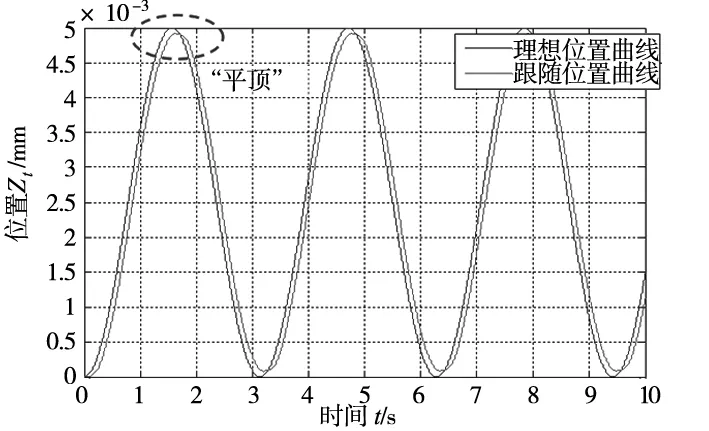
图8 位置跟随曲线
由图7、图8可以看出,在速度跟踪过程中,由于非线性摩擦力的存在,当速度穿过零点时,速度跟踪曲线发生严重变形,出现跟踪死区的情况,这也就是我们常说的“速度过零”现象,从而导致位置跟踪出现明显的“平顶”现象,因此需要对非线性摩擦力进行消除。
对LuGre非线性摩擦力进行消除前,需对LuGre摩擦模型的参数进行辨识。针对传统遗传算法的局限,本论文提出了一种改进遗传算法来提高LuGre摩擦模型参数辨识的有效性与准确率。
3 改进遗传算法摩擦参数辨识与补偿
遗传算法是一种自适应启发式概率性迭代式全局搜索算法[13]。然而,在对LuGre摩擦模型参数进行辨识时,由于高度非线性和一阶微分项的存在,遗传算法辨识结果容易陷入局部最优[14-15]。
3.1 改进遗传算法的设计
针对传统遗传算法在LuGre摩擦模型的参数辨识容易陷入局部最优的问题,基于传统遗传算法,本论文提出了通过设立不同单轮进化初始辨识亲代种群,并进行多轮进化的方法,来解决高度非线性微分LuGre摩擦模型参数辨识局部最优问题,从而获取参数全局最优解。在进行改进遗传算法的设计前,为了模型以及程序设计的实现,对式(5)的LuGre摩擦模型进行了离散化设计:
(6)

设摩擦力的误差为:
e(k)=FfR(k)-FfI(k)
(7)
式中,FfR(k)为实际LuGre摩擦力,FfI(k)为识别的LuGre摩擦力。
定义目标函数:
(8)
式中,N为采样次数,辨识目标为使适配值J最小。
然后,再进行改进遗传算法的设计,其具体实现步骤为:①初始化:设定待辨识参数;设定进化轮数与单轮进化代数;设定各待辨识参数搜索空间。②根据各待辨识参数搜索空间,产生单轮进化初始亲代种群,产生方法如式(9)所示。
(9)

(10)
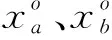
Pm(g)=0.02-(0.02-0.001)g/G
(11)
式中,Pm为变异概率,g为当前进化次数,G为单轮最大进化次数,同时计算该子代种群各个体对应适配值。④判定单轮进化代数是否完成,若未完成,利用排位次法选取相应种群数量的当代适配值最高个体群作为新的亲代种群返回到第三步,若完成,则进入第五步。⑤获取单轮进化最优解并存储。⑥判定进化轮数是否完成,若未完成,返回第二步,若完成,则进入第七步。⑦计算各轮进化最优解适配值,选取全局最优解输出。
以上步骤可由图9来表示。

图9 改进遗传算法流程图
3.2 LuGre摩擦模型参数辨识实验
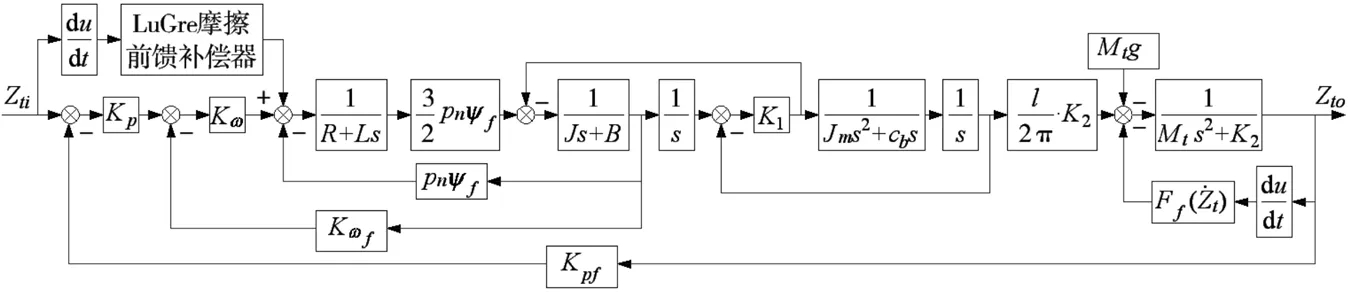
图10 LuGre摩擦前馈补偿模型
根据LuGre摩擦模型的数学表达式(式6),设定6个待辨识的参数vs=0.0125m/s,Fc=3.82N,Fs=8.16N,σ0=84000N/m,σ1=260N·s/m,σ2=28N·s/m,其搜索空间分别为vs∈[0,0.1],Fc∈[0,50],Fs∈[0,50],σ0∈[60000,100000],σ1∈[0,500],σ2∈[0,100],进化轮数G1=20,单轮进化次数G2=200。
在Matlab下分别进行传统遗传算法和改进遗传算法的参数辨识仿真实验,得到在传统遗传算法下连续10次进行参数辨识的结果和在改进遗传算法下连续10次进行参数辨识的结果如表1、表2所示。

表1 传统遗传算法下LuGre摩擦参数辨识结果
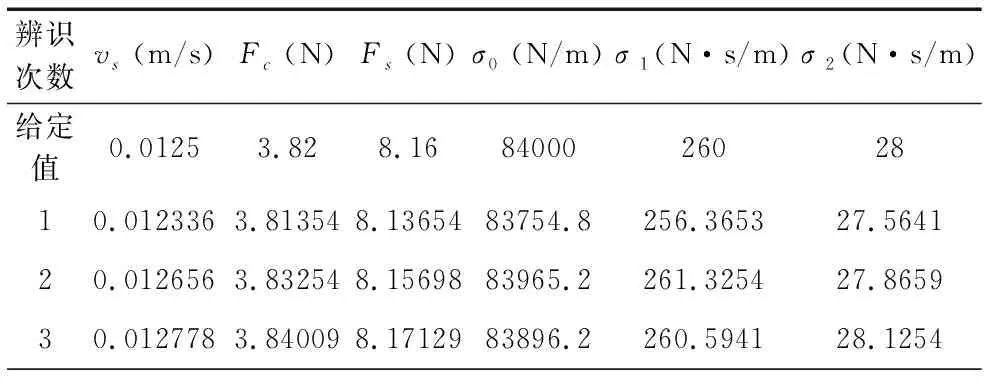
表2 改进遗传算法下LuGre摩擦参数辨识结果

续表
由表1、表2比较可知,在对高度非线性LuGre摩擦模型的参数进行辨识的过程中,传统的遗传算法辨识结果出现局部最优的概率较大;而本文提出的改进遗传算法,通过离散化LuGre摩擦模型,可一次对LuGre摩擦模型的6个动、静态参数进行辨识,并将辨识结果陷入局部最优的概率从0.3左右降低到了0.1以下,提高了参数辨识的正确性。同时,辨识误差从10%左右降低到了3%以内,辨识精度得到了提高。
3.3 基于LuGre摩擦模型的摩擦补偿实验
如图10所示,在Z轴直线位置伺服装配臂系统中,采用前馈补偿的方式对Z轴直线伺服装配臂的LuGre摩擦力扰动进行补偿。
根据图中前馈摩擦补偿模型设计LuGre摩擦前馈补偿器为:
(12)
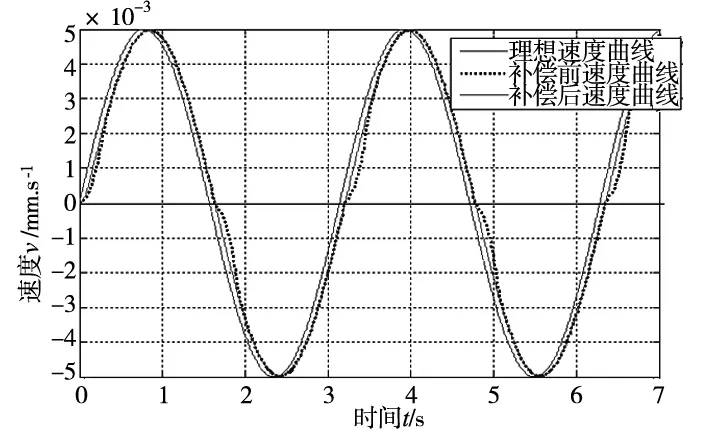
图11 补偿前后速度跟随曲线

图12 补偿前后位置跟随曲线
根据表2中改进遗传算法辨识结果取vs=0.01254m/s,Fc=3.822N,σ0=84012N/m,Fs=8.155N,σ1=260.5N·s/m,σ2=27.9N·s/m,得到补偿结果如图11、图12所示。
由图11、图12可知,根据改进遗传算法所获取的非线性摩擦模型参数,对Z轴直线位置伺服装配臂进行前馈补偿,做速度跟踪时,当速度穿过零点,速度跟踪曲线严重变形现象消失,没有出现跟踪死区的情况,“速度过零”现象得以消除;与此同时,位置跟踪中的“平顶”现象消除。由此可见,基于改进遗传算法所获取的非线性摩擦参数,对Z轴直线位置伺服装配臂的非线性摩擦力进行前馈补偿,可有效地消除非线性摩擦力对直线伺服系统的影响,从而提高了该直线伺服装配臂系统的伺服性能。
4 结论
在精密伺服机械臂运动系统中,非线性摩擦力将对系统的动静态性能带来不利影响,因此需消除其所带来的干扰。本文首先针对非线性摩擦力对精密伺服机械臂的动静态性能的影响,利用LuGre摩擦模型来对非线性摩擦力进行数学描述,通过对LuGre摩擦模型离散化求解,解决了“分步辨识”实验量大、辨识过程复杂的问题,实现了“一步辨识”;然后针对现有LuGre摩擦模型参数辨识方法的局限性,提出了一种改进遗传算法,对LuGre摩擦模型的参数进行辨识,结果表明,相比于传统的遗传算法,所提的改进遗传算法将辨识结果陷入局部最优的概率从0.3左右降低到了0.1以下,辨识误差从10%左右降低到了3%以内,辨识有效性和精度均得到了提高;最后根据辨识的参数,设计了前馈补偿器对LuGre非线性摩擦力进行了补偿,实验结果表明,通过前馈补偿可有效地消除非线性摩擦力对精密伺服机械臂系统的动静态性能的影响,提高精密伺服系统性能。

