轮拱罩充满率对整车气动特性的影响
余霄雁, 贾 青, 杨志刚,2
(1. 同济大学 地面交通工具风洞中心,上海 201804;2. 中国商飞 北京民用飞机技术研究中心,北京 102211)
随着环境问题的越发严重,汽车的节能性和环保性越来越受到厂商和消费者的重视.减小汽车所受空气阻力是减少汽车能耗和排放的重要手段.20世纪90年代,Mercker等[1]和Wickern等[2]指出,对于一辆现代小型汽车,车轮和轮投罩所受空气阻力约占总空气阻力的30%,这还不包括车轮和轮拱罩对其他部分的空气动力学影响.因此,车轮空气动力学研究对整车减阻有着重要的意义.
20世纪早期,Morelli[3]和Fackrell等[4-5]通过风洞试验进行了车轮空气动力学研究,但由于试验技术的限制,研究存在着较大的局限性.近年来,随着电脑技术的进步,计算流体力学(CFD)方法得到了快速发展.CFD方法可以克服试验条件限制,减少人力物力成本,因此基于CFD方法的旋转车轮数值仿真研究得到发展.近年来,针对旋转车轮气动性能机理的研究仍然是一个很重要的课题[6-12].
在车轮与整车的空气动力学影响研究中,轮拱罩的影响是一个非常重要的部分.Cogotti[13]采用风洞试验法研究了带有轮拱罩的车轮的气动特性,研究对象为只有2个车轮的简化车型,结果表明轮拱罩的体积越小,升阻力越小.Fabijanic[14]通过风洞试验采用类似的二轮模型进行了针对轮拱罩深度、直径和车轮直径等参数的研究,但结果与Cogotti的结果有所矛盾.Soederblom等[15]利用CFD方法研究了重型车辆不同轮拱罩参数对整车气动性能的影响,并得到了和Cogotti类似的结论.Regert等[16]则对轮拱罩中的涡结构进行了研究,发现了多处不同的非定常涡结构,该研究使用的模型仍然为Fabijanic所使用的二轮模型.
虽然已有一些研究车轮与轮拱罩的文献,但采用的模型基本都是二轮模型,与真实的四轮车辆之间存在较大差别.本文将使用某型量产轿车模型,通过改变轮拱罩直径的方式,改变车轮在轮拱罩中的充满程度,研究不同充满率下旋转车轮对整车流场的影响,并分析其机理.
1 计算设置
1.1 几何和网格
本文所选择的车型为小型三箱轿车,车长4.32 m,车宽1.66 m,车高1.15 m,正面投影面积1.82 m2.为简化计算,该模型省去了前端进气模板以及雨刷器、后视镜等凸起物,下车身也用平板代替原有的部件.车轮为五辐车轮,带有刹车盘且轮毂不封闭;轮胎参数为235/40 R17,没有胎纹,车身离地间隙为200 mm.在车轮接地处使用了一个小台阶以避免该处出现低质量网格.为了便于描述,定义车轮直径为D0,轮拱罩直径为D′,测量可得该车型D0=622 mm,D′=718 mm.由于汽车的表面形状比较复杂,因此车身和车轮面网格均选择三角形网格,体网格则采用混合网格.在近壁面生成边界层网格,车身附近区域使用四面体网格,在其他大部分区域使用结构化六面体网格,这可以在获得较高质量网格的同时减小网格数量,从而减小计算资源的消耗.几何模型和计算网格如图1所示.
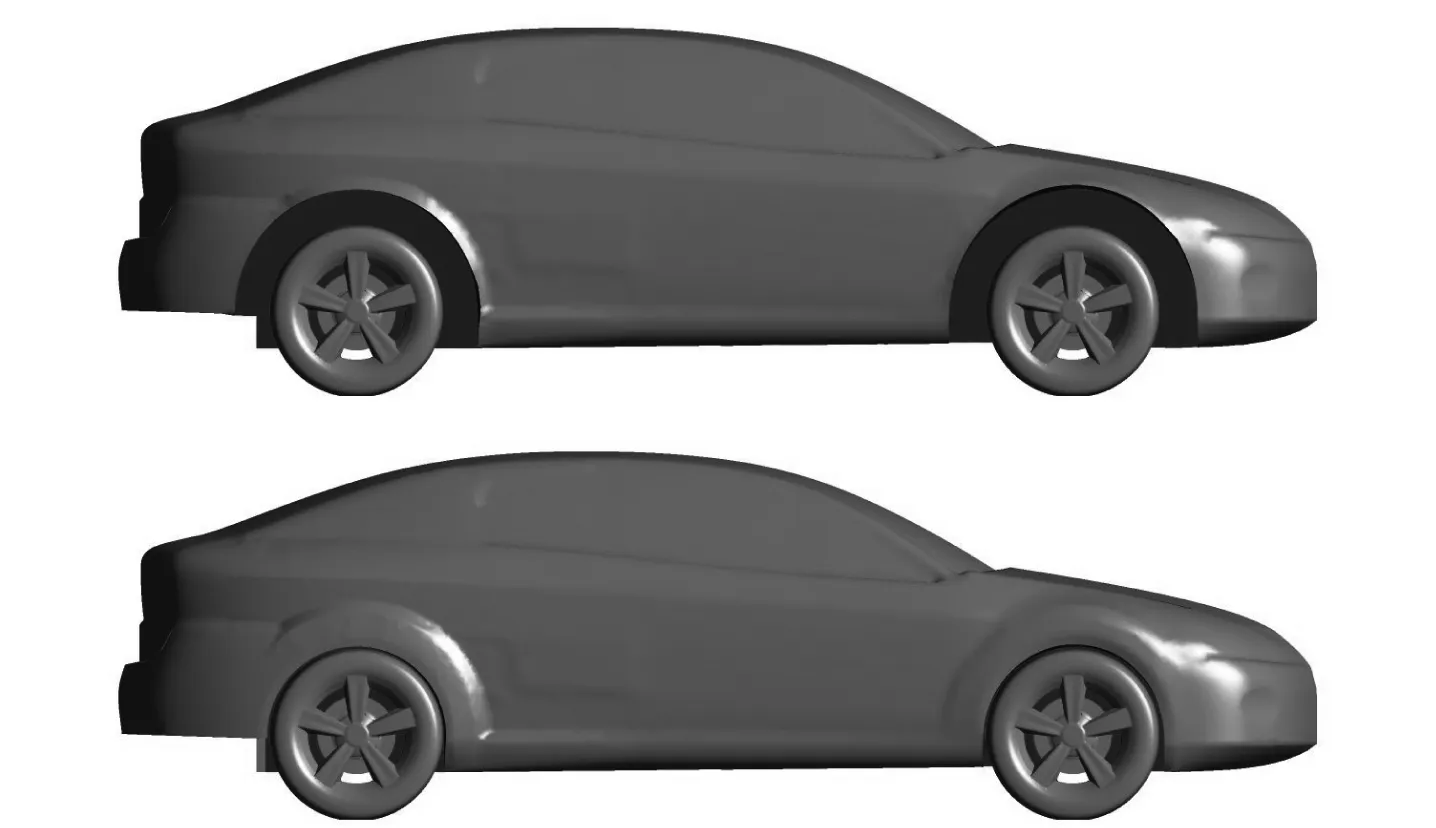
a 轮拱罩不同的整车和车轮模型
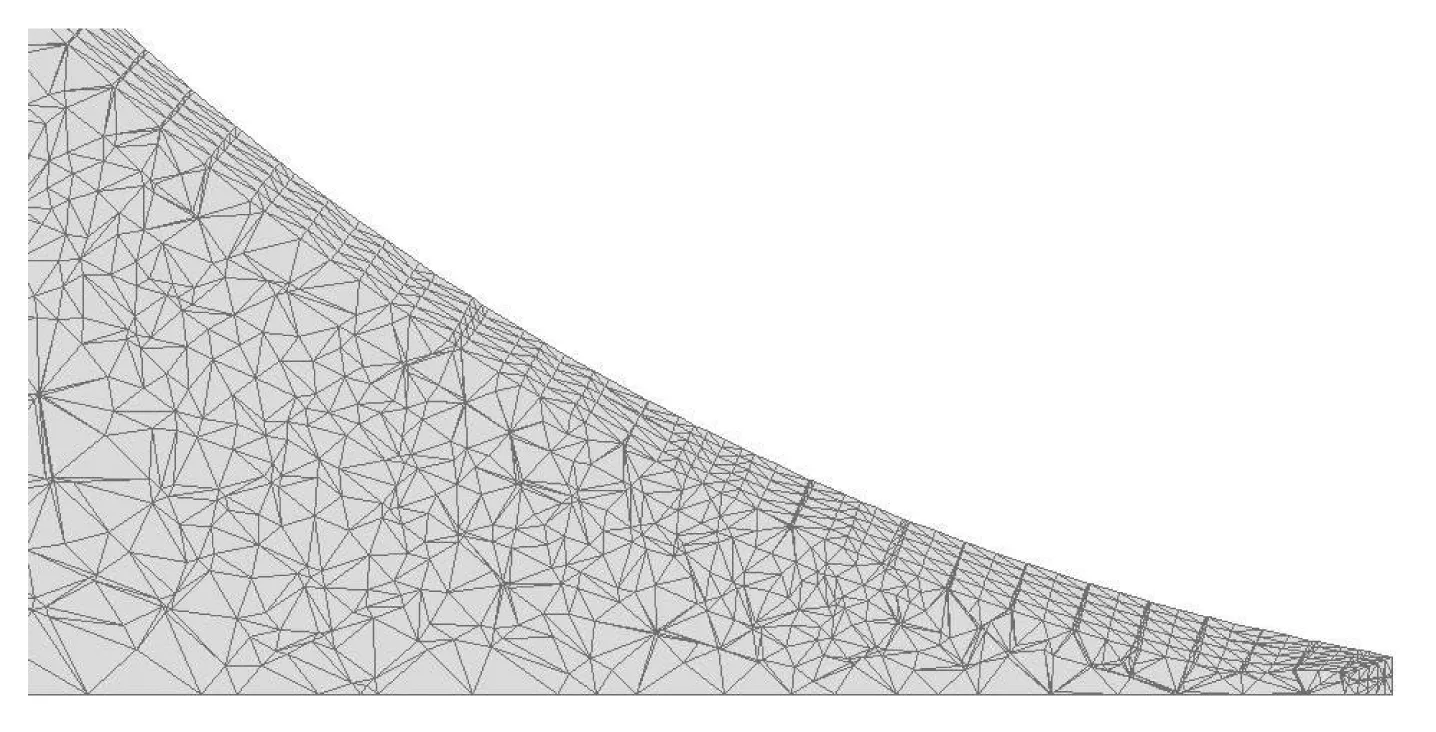
b 车轮近地区体网格图1 几何模型和计算网格Fig.1 Geometries and meshes
为避免边界干扰,将阻塞比控制到5%以下[8],设置计算域总长60 m,宽12 m,高10 m.此时阻塞比为1.52%,基本可以避免由于阻塞效应产生的误差[10,15].整个计算域如图2所示.

图2 计算域Fig.2 Whole computational domain
1.2 计算模型
本文中所有CFD计算均采用Fluent 16软件,根据以往研究结果[17],采用定常雷诺平均N-S(RANS)方程配合Realizablek-ε湍流模型进行求解,该湍流模型对气流旋转和大尺度分离有较好的预测结果[18].壁面函数选择非平衡壁面,该壁面函数对表面压力分布的近似拟合较为理想[16].
1.3 边界条件
计算域的入口设置为速度入口,速度大小为30 m·s-1,模拟汽车高速行驶工况.此时车轮雷诺数为1.26×106,符合Cogotti[13]提出的车轮雷诺数要求.出口设置为压力出口,参考压力为零.车身设置为静止壁面,车轮均设置为旋转壁面,并且车轮最外缘的线速度与来流速度一致.地面设置为移动地面,速度大小为来流速度.其余壁面均设置为对称边界,以避免壁面干扰.
1.4 网格无关性
为消除由于网格数量不足导致的数值误差,有必要通过加密网格的方法进行网格无关性研究.通过改变体网格增长率进行网格加密,得到5个网格数量不同的算例,并通过评价它们的气动阻力系数CD和气动升力系数CL在不同网格数时的变化以验证网格无关性.5个算例的CD和CL计算结果如表1所示.

表1 网格无关性验证Tab.1 Grid independence validation
由表1可知,当体网格增长率小到1.10,总网格数达到约1 900万时,CD和CL的值基本不变,满足网格无关性要求.因此,本文所有算例的体网格增长率都将采用1.10,所有算例的网格数都控制在1 900万左右.
2 结果与讨论
2.1 气动力
为描述车轮在轮拱罩中的充满程度,定义充满率n=D0/D′,本文在不改变车轮和离地高度的前提下,通过修改车身的几何和网格来改变轮拱罩的直径,从而改变轮拱罩的充满率,然后分析充满率对整车气动阻力系数CD和气动升力系数CL的影响.
本文中共进行2组仿真.第1组的车轮直径定义为D1,且D1=0.90D0=559.8 mm;第2组的车轮直径定义为D2,D2=1.00D0=622.0 mm.每一组共有7个算例,对应7个不同的轮拱罩直径,同时保证2组算例中的充满率是一一对应的.选定的充满率和对应的轮拱罩直径如表2所示.需要说明的是,常见轿车的轮拱罩充满率约为75%~85%,为了使差异更加明显,本文中轮拱罩充满率的变化范围略有扩大.
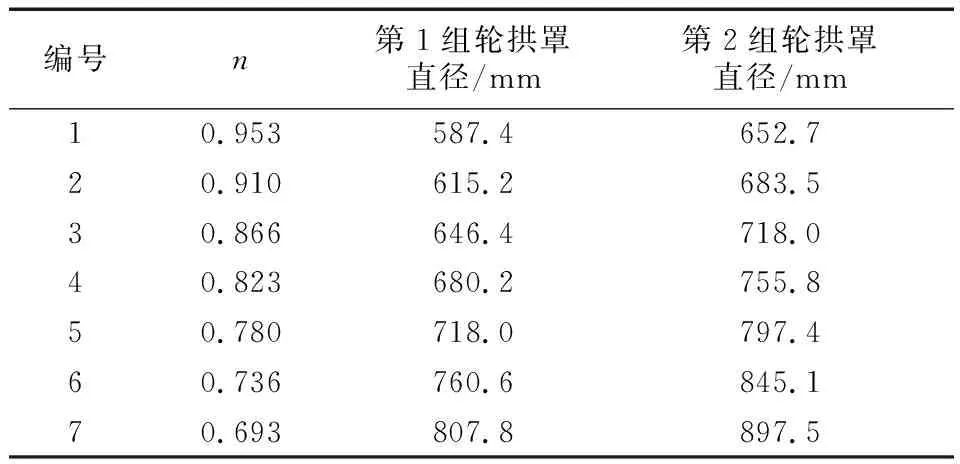
表2 充满率和对应的轮拱罩直径Tab.2 Filling ratio and wheel housing diameter
2组仿真结果中CD或CL随充满率的变化如图3所示,同时给出了Cogotti[13]和Fabijanic[14]的试验结果进行对比.可以看出,随着轮拱罩直径上升,充满率减小了0.260(约27.3%),阻力系数增加了0.057(约19.5%),升力系数下降了0.087(约28.8%).阻力的变化趋势和Cogotti[13]的试验结果一致,然而升力的变化趋势则正好相反.升力系数趋势的不符可能是因为车型和试验参数的不同导致的.Cogotti[13]使用的是接近于水滴形的二轮车,和真实的四轮轿车有着显著不同,同时地面是静止的,这也和本文及实际情况不符.文献[10]中指出,升力系数与车身下底面的流动状态有着密切的关联,并且对车身和车型的变化非常敏感.阻力系数和升力系数的结果表明,虽然模型不同,但是在充满率减小时,整车阻力减小的趋势是一致的;升力的变化则与车型和试验参数密切相关,无法得到一个确定的变化趋势,因此在进行整车气动升力研究时,应使用精度更高的仿真或试验手段.
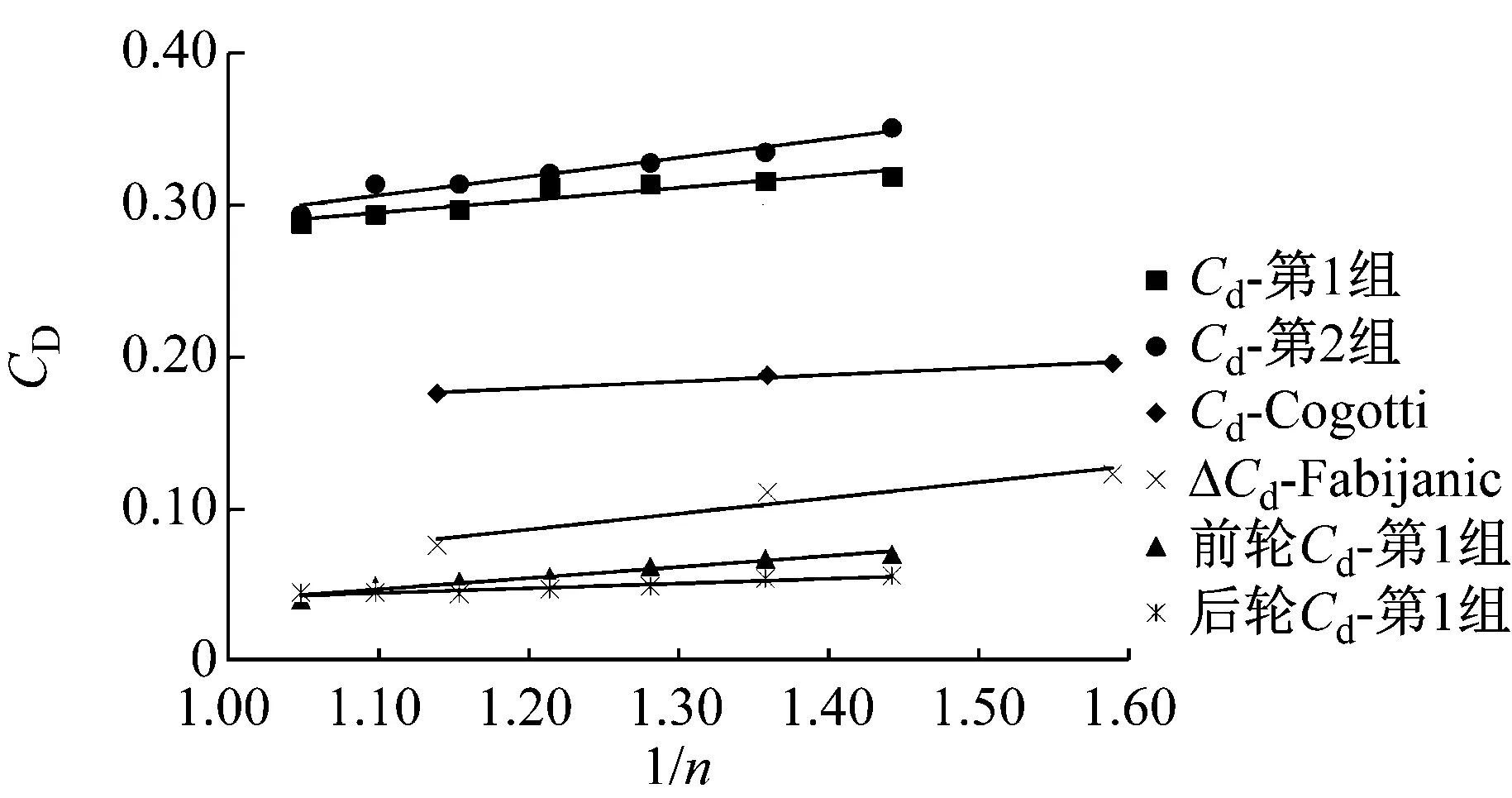
a 阻力系数CD
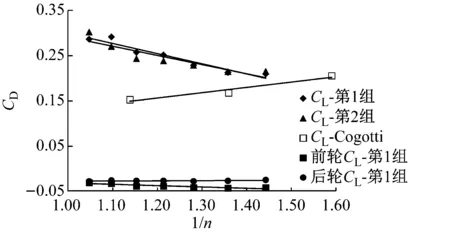
b 升力系数CL图3 气动力系数变化Fig.3 Variation in drag and lift coefficients
从图3可以看到,前后轮区域的阻力均随充满率减小而增加,前轮的阻力增量比后轮更大.前后轮区域的升力变化不大,表明整车的升力变化基本都来自于车身.因此,对于阻力变化的讨论需要同时考虑车身和车轮的影响,而对升力变化的讨论则应主要集中于车身上.
2.2 表面压力
气动力系数的变化直接归因于表面压力系数的变化,因此有必要通过研究车身表面压力来分析气动力变化的机理.为了简化工作,下文只选择了第2组计算中的编号为1、3、5、7的4个算例(算例1~4)进行对比分析.图4a、c分别显示了车身中心线表面压力系数分布.为使差异更明显,将上下表面中压力差值较大的区域适度放大,如图4b、d所示.从图4可以看到:除背部压力略有下降外,车身上表面压力系数几乎不随充满率下降而变化;下表面压力系数则随着充满率下降而明显减小,尤其是在前轮区域.背部压力的下降及下表面压力的减小与阻力和升力的变化是一致的,但为了解释表面压力变化的原因,仍然需要进一步对流场进行分析.
2.3 流场分析与讨论
为解释轮拱罩充满率对整车流场的影响机理,有必要对整车周围流场进行分析.图5为左后轮附近车身表面油流图.从图5可以很清楚地看到,轮拱罩直径的增加会使轮拱罩内出现原本难以观察到的涡(见图5中①),并且这个涡在轮拱罩直径增加时有明显增大,这与Regert等[16]的结果一致.另外,随着轮拱罩直径的增加,轮腔后部、车身侧壁上的一对涡(见图5中②)的尺度也有所增大.这说明充满率变化会影响轮拱罩周围的流场,而且这种影响从轮拱罩开始,随后向下游发展,从而改变车身尾流流场.这种影响表现在涡上,则是改变涡的位置、数量和大小等,而正是涡的改变导致了整车表面压力的变化,最终导致阻力系数和升力系数的变化.
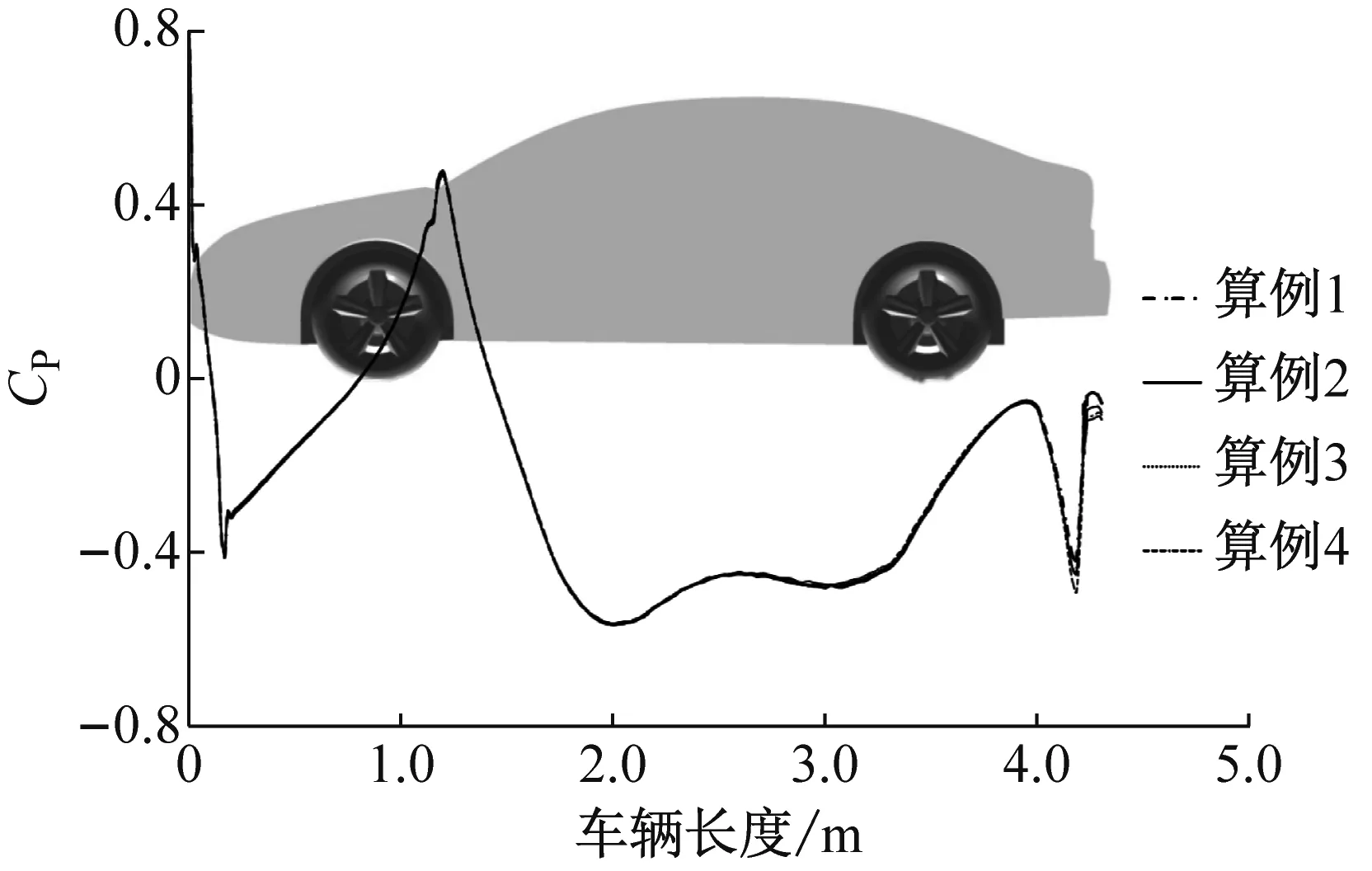
a 上表面

b 上表面(背部附近)

c 下表面
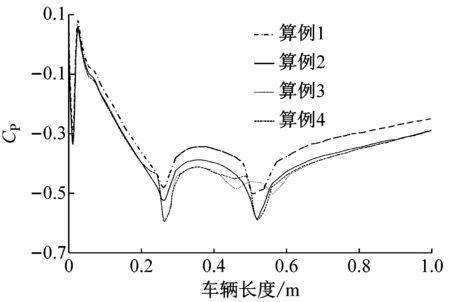
d 下表面(前轮附近)图4 车身中心线表面压力系数分布Fig.4 Surface pressure coefficient distribution on the body center line

算例1算例2算例3算例4
图5左后轮附近车身表面油流图
Fig.5Wallshearstreamlinesneartheleftrearwheel
图6显示了平面z=0.5 m处的湍动能.当充满率下降时,各车轮区域的湍动能明显上升,说明车轮区域的涡强度也有所加强,这与车轮阻力上升的结果是吻合的.同时,在车轮区域外,尾涡的湍动能也有所增强,这与图5的结果是一致的.通过进一步的观察可以看出,前轮拱罩附近的湍动能很强,并且能向车尾方向拖动较长的距离,这意味着前轮拱罩不仅自身的涡强度很大,还会增强后轮拱罩和尾涡的强度;后轮拱罩中的湍动能虽然相比于前轮拱罩湍动能较低,但是后轮拱罩高湍动能的气流会增强侧壁涡(见图5②),并通过侧壁进入尾涡,使尾涡强度上升.

算例1算例3算例5算例7
图6z=0.5m平面湍动能
Fig.6Turbulentkineticenergycontoursontheplanez=0.5m
除湍动能外,使用涡量Q判据也可以显示涡的大小和强度[16].图7是右前轮和右后轮附近的Q等值面(Q=100 s-2).从图7可以看出,各车轮区域涡强度的上升更加明显,后轮涡在增强的同时,会沿着车身向后延伸,从而增强车背侧面涡的强度以及尾涡的强度,这也进一步证明了图5和图6的结果.
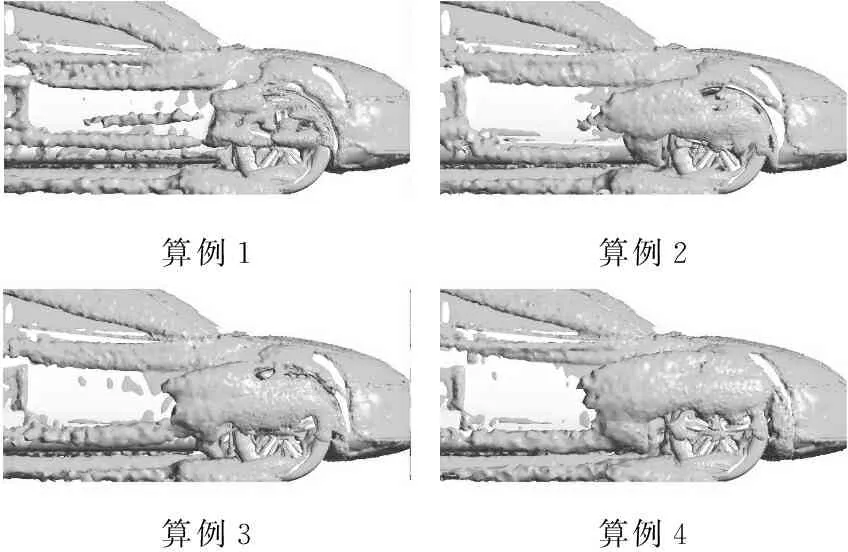
算例1算例2算例3算例4

a 右前轮
b 右后轮
图7Q等值面(Q=100s-2)
Fig.7Iso-surfaceofQ(Q=100s-2)
图8显示了车轮和轮拱罩附近的速度流线.随着充满率减小,进入轮拱罩的来流增加,大部分气流在车轮的下部被阻塞并改变方向.一部分气流从外侧经过轮胎,但仍有相当一部分向上并进入轮拱罩.轮拱罩内的气流在腔体内的不同位置分离,其中两处比较明显:一是在靠近轮拱罩前缘的位置产生的分离涡(见图8①),这处分离会对腔内气流的涡量有一定的加强;二是车轮上后部的分离涡以及在车轮的顶部形成的分离涡(见图8②),该处的分离类似于在孤立车轮顶部的分离.这意味着如果轮拱罩直径足够大,被车轮外壳抑制的孤立车轮特征将重新出现.以这两处为代表的轮拱罩内分离会使进入轮拱罩的气流产生更多的涡,从而导致涡量增强,这和图7的结果是吻合的.
从图8还可以看到,当充满率较小时,更多高湍动能气流会从后轮壳体进入尾流区和基区.这也与尾流区的较高涡量(见图7)以及背压力的变化一致.
综合以上分析,可以得到充满率变化对整车气动阻力的影响机理.当轮拱罩直径变大,充满率变小时,更多的气流进入轮拱罩内.罩内区域的流动受到轮拱罩和旋转车轮的干扰,并产生以轮拱罩前缘内侧和车轮上后部为代表的众多分离.这些分离随着轮拱罩内流量的增加而变强,从而涡的强度增加,湍动能和涡量均上升,前轮区域的上升比后轮更剧烈.车轮周围湍动能的增加是车轮阻力增加的主要原因,因此这可以解释车轮阻力随充满率减小而上升,并且前轮阻力的增加大于后轮的原因.
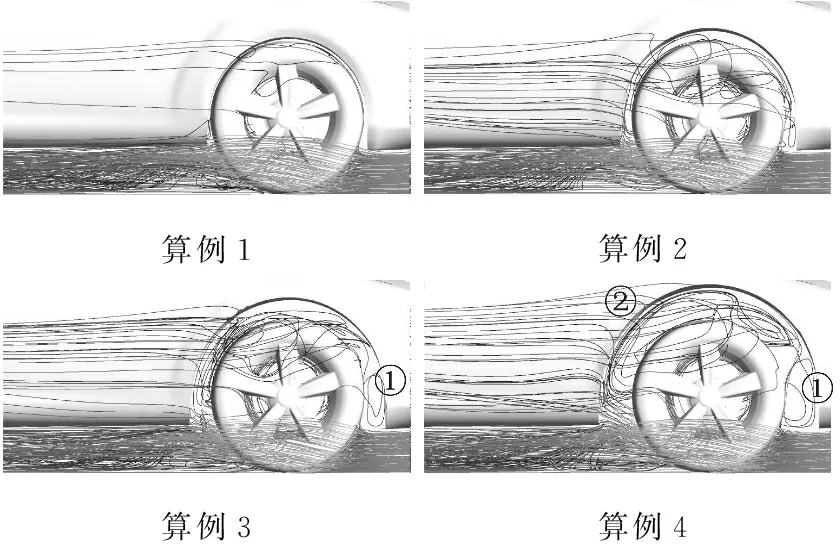
算例1算例2算例3算例4
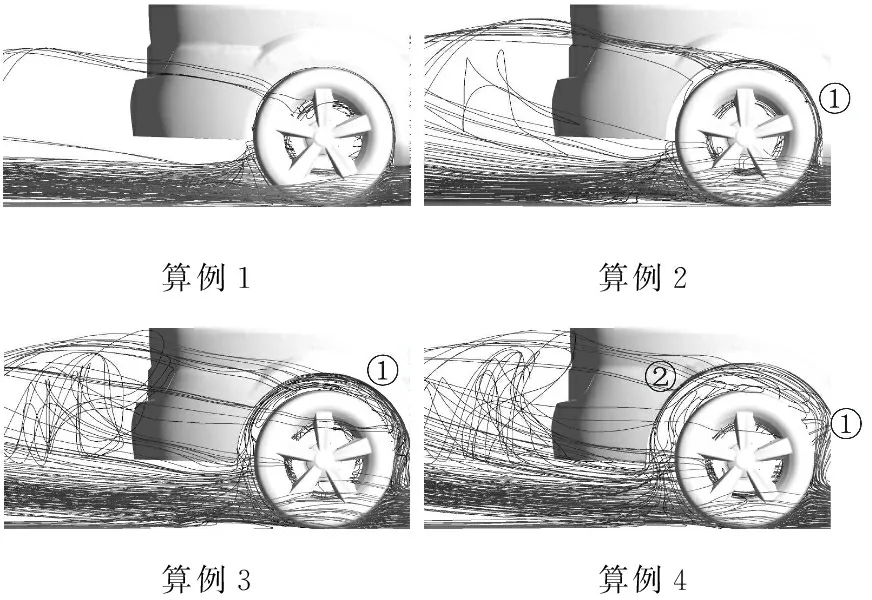
a 前轮
b 后轮
图8车轮附近流线
Fig.8Velocitystreamlinesaroundwheels
与此同时,带有强大涡量的气流不仅会作用于轮拱罩内,还会从轮拱罩(尤其是后轮拱罩)延伸到车身背部区域,从而增强尾涡.尾涡的增强则会导致背部压力减小,最终使得车身阻力增加.车轮和车身两部分阻力的同时增强,最终引起了总阻力的增加.
除了气动阻力系数,也有必要分析不同充满率使气动升力系数产生变化的原因.从图3可以看出,升力的变化主要来自车身,同时从图4又可以看到,在充满率下降时,整车升力系数减小的原因基本来自于下车身压力的减小,因此有必要分析车身下部的气流流动情况.图9是平面z=0.15 m处的速度等值面(该平面位于下车身下部),仅显示算例4减去算例1所得差值的正值部分(即算例4中速度比算例1中大的部分).从图9可以看到,在充满率下降时,前后车轮后方的气流流速都明显加快.同时,车底气流的流速也略有上升.下车身气流速度加快导致车身下表面压力的减小,最终引起气动升力的减小,这和图3中升力变化结果也是吻合的.这部分的高速流很可能来自于气流与旋转车轮的相互作用.由于更多的气流进入了轮拱罩,导致更多的气流被旋转车轮所加速,其中一部分从轮拱罩下侧流出,并进入车身底部区域,因此车身底部流动速度也更快,下表面压力则有所降低.然而,该现象未在Cogotti[13]的研究中发现的原因尚不清楚,可能与下车身的结构有关,有待进一步的探索.

图9 z=0.15 m平面速度差值云图Fig.9 Velocity difference contours on the plane z=0.15 m
3 结论
(1) 当轮拱罩直径增大(充满率减小)时,整车气动阻力系数增大,整车气动升力系数有所减小.整车阻力系数的增加来自于车身和车轮两部分,升力系数的减小则基本仅有车身的贡献.
(2) 随着充满率的减小,车身背部压力有所降低,导致车身阻力系数增大;车身底部表面压力下降,导致车身升力系数减小.这是车身气动力变化的直接原因.
(3) 充满率减小时,更多的气流进入轮拱罩内.由于旋转车轮和轮拱罩的阻塞作用,轮拱罩内的分离现象加剧,这增强了轮拱罩内的涡量,产生了车轮区域的阻力.
(4) 由于受到轮拱罩的干扰,经过车轮的气流涡量有所增强,后轮拱罩的干扰尤为明显,使后轮气流湍动能增加的同时沿车身侧面延伸,进入尾流中,导致尾涡增强,这是背压降低的主要原因.
(5) 当充满率减小时,轮拱罩内的高速气流流量增加.高速气流通过轮拱罩进入车身底部区域,导致车身底部附近的速度增加,合理解释了表面压力系数减小的原因.

