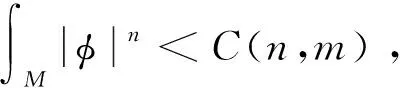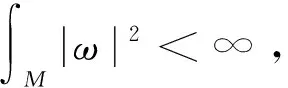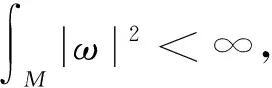双曲空间中子流形的刚性

刘建成，曹亚春

(西北师范大学数学与统计学院，甘肃兰州 730070)

0 引言及主要结果

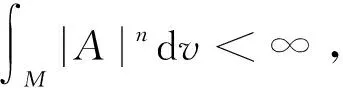
很自然地考虑到双曲空间中的子流形是否也有一些类似的结果,围绕这一问题,Seo[7]证明了:若双曲空间中极小子流形Mn满足第二基本形式A的Ln模小于一个适当的常数，那么子流形上不存在非平凡的L2调和1-形式,它蕴含的是Mn仅有一个端.周俊东[8]研究了双曲空间中n维完备极小子流形Mn,证明了若Mn的第二基本形式A的模长平方的上确界小于一个仅依赖于n的正常数,那么子流形Mn仅有一个端.

文中将关于A或φ的点态条件减弱为整体积分条件,证明了双曲空间中具有常平均曲率H的完备非紧子流形依然具有类似的刚性结果,并且子流形Mn上仅有一个非抛物型的端.

定理1设Mn(n≥5)是双曲空间Hn+m(-1)中具有常平均曲率H的完备非紧子流形,假设H≤α,0≤α

则H1(L2(M))={0},并且Mn仅有一个端.

2 预备知识及引理

设Mn(n≥5)是双曲空间Hn+m(-1)中的n维完备非紧子流形.在Hn+m(-1)中选取局部单位正交标架场{eA},1≤A≤n+m,使得限制在Mn上时,{ei}与Mn相切,{eα}与Mn正交,其中求和指标取值范围如下:

1≤i,j,…≤n,n+1≤α,β,…≤n+p.

φαX,Y=X,YH,eα-AαX,Y

容易验证，每一个线性映射φα都是无迹的,并且

φ2=0当且仅当Mn是全脐的.

记H1(L2(M))为M上所有L2调和1-形式构成的空间,即

此外,定义Mn的第一特征值λ1(M)为[9]

为了完成定理的证明,我们需要以下引理.

引理1[10]设Mn是双曲空间Hn+m(-1)中具有常平均曲率H的完备非紧子流形,若H≤α,0≤α

引理2[11]设Nn+m是截曲率非正的完备连通流形,Mn是Nn+m中的完备非紧子流形,那么对于任意的1≤p≤n,下面不等式成立：

引理3[8]设ω是n维黎曼流形M上的一个调和1-形式,则

ω2.(1)

根据Bochner公式有

Δω2=(ω2+Ric(ω,ω)).(2)

另一方面

Δω2=2(ωΔω+ω2).(3)

结合(1)～(3)式得

将(5)式代入(4)式整理得

3 定理1的证明

(6)式结合Cauchy-Schwarz不等式得

应用散度定理可得

根据M上第一特征值λ1的定义,结合引理1得

引理2结合Holder不等式得

其中

对于任意的ε>0,应用Cauchy-Schwarz不等式，有

将(12)式代入(11)式整理得

固定一个点x0∈M,对于任意的r>0,截段函数f满足以下性质:

应用截段函数的性质(13)整理得

ω=0,Hω=0.

H1(L2(M))={0}.

根据文献[13]中的引理2.2可得Mn仅有一个非抛物型的端.