基于本构方程的搅拌混合体系均匀性定量评价方法研究
潘家保,齐国良,王文昌,高 洪
(1.安徽科达机电有限公司,安徽 马鞍山 243000;2.安徽工程大学 机械与汽车工程学院,安徽 芜湖 241000)
搅拌混合体系均匀性评价是其搅拌混合效果优良的重要指标,也是混合体系制备过程中不可或缺的重要环节之一.工业生产中常用的混凝土、润滑脂等均属于搅拌混合体系[1-2].无论是混凝土或润滑脂,混合体系均匀性均将会对其性能产生直接影响[3-4].然而,混合体系均匀性评价方面,目前还缺乏统一的定量评价方法.针对混凝土而言,搅拌均匀性参考指标大多集中采用混凝土塌落度的波动性或混凝土试件的抗压强度[5].而润滑脂均匀性评价方面的研究报道较少,主要集中于添加剂在润滑脂胶体体系内部分散均匀性方面[6].
与此同时,混凝土、润滑脂等混合体系在承受剪切过程中均表现出特有的流变特性.严锐[7]探究了含有不同组成的泡沫混凝土流变性能变化规律,并采用了Herschel-Bulkey(H-B)模型对其流变数据进行了数值拟合得出了其流变参数.焦登武[8]等探究了不同骨料裹浆厚度混凝土的流变特性,并采用Bingham模型拟合出润滑脂的流变参数.可以发现,借助流变模型可对混凝土的流变特性进行较为准确的定量分析.研究人员同样对润滑脂的流变特性展开了广泛研究,并采用了不同流变本构方程对润滑脂的流变特性进行了定量分析,取得了较好的定量表征效果[9-11].对于稳定均匀混合体系而言,流变参数将是确定值,即流变参数为均匀混合体系的特征指标.因而,从搅拌混合体系不同位置进行取样进行流变特性测试,探究流变参数变化情况,将是进行搅拌混合体系均匀性评价较为有效的方法.
基于此,以润滑脂为例,开展其流变特性测试,选取合适流变模型,采用数据拟合方法获取其流变参数,以此作为润滑脂均匀性评价的指标参数.为进一步揭示其机理,探究了润滑脂的混合体系微观结构及动态演化规律,分析了基于流变本构方程进行搅拌混合塑体系均匀性评价的可行性及优势.研究可为搅拌混合体系均匀性定量评价提供方法指导.
1 评价方法与实验研究
1.1 流变曲线分析
研究流体流变特性变化规律主要借助物质的流变曲线.流变曲线反映了流体在承受剪切过程中的剪切应力与剪切速率的变化关系.对于剪切应力和剪切速率变化关系符合线性规律的流体,即牛顿内摩擦定律,称之为牛顿流体,如式(1)所示.
τ=ηdu/dy,
(1)
式中,τ为剪切应力;η为粘度;du/dy为剪切速率.所有不符合牛顿内摩擦定律的流体,统称为非牛顿流体.非牛顿流体展现出复杂的流变特性变化规律,依据其流变曲线变化规律,可以分为膨胀性流体、假塑性流体、塑性流体和宾汉流体等,如图1所示.
混凝土、润滑脂等均属于塑性流体,其剪切流动的应力应变规律较复杂,研究人员也提出了相应的定量表征模型,如H-B模型[12]、四参数模型[13]:
H-B模型[12]
(2)
四参数模型[13]
(3)
流变特性曲线表征的是物质在承受剪切过程中的应力和应变变化关系,对于稳定的搅拌混合体系而言,其流变曲线是确定的.为此,考察混合体系是否达到均质化的效果,可以通过对混合体系不同区域进行取样,开展流变实验测试,进而得出其流变方程.比对流变参数是否一致,进而考察其混合的均质效果.为了对该方法进行详细阐述,选用润滑脂作为实验材料,开展流变特性测试,选定数学模型,开展数据拟合,并进一步从润滑脂结构角度揭示方法的可行性.
1.2 实验研究
(1)实验材料.选用中石化NLGI00锂基润滑脂作为实验材料,其主要性能参数如表1所示.

表1 NLGI00锂基润滑脂的主要性能参数
注:①依据40 ASTM D-445;②依据ASTM D-566;③依据ASTM D-217
(2)流变测试实验仪器.流变测试采用安东帕(德国)Physica MCR302旋转流变仪,测试模块选用圆筒测试系统,圆筒直径为20 mm,如图2所示.测试模块的转子转动,测试圆筒内部流体形成剪切流动效果,进而开展润滑脂的流变特性测试.
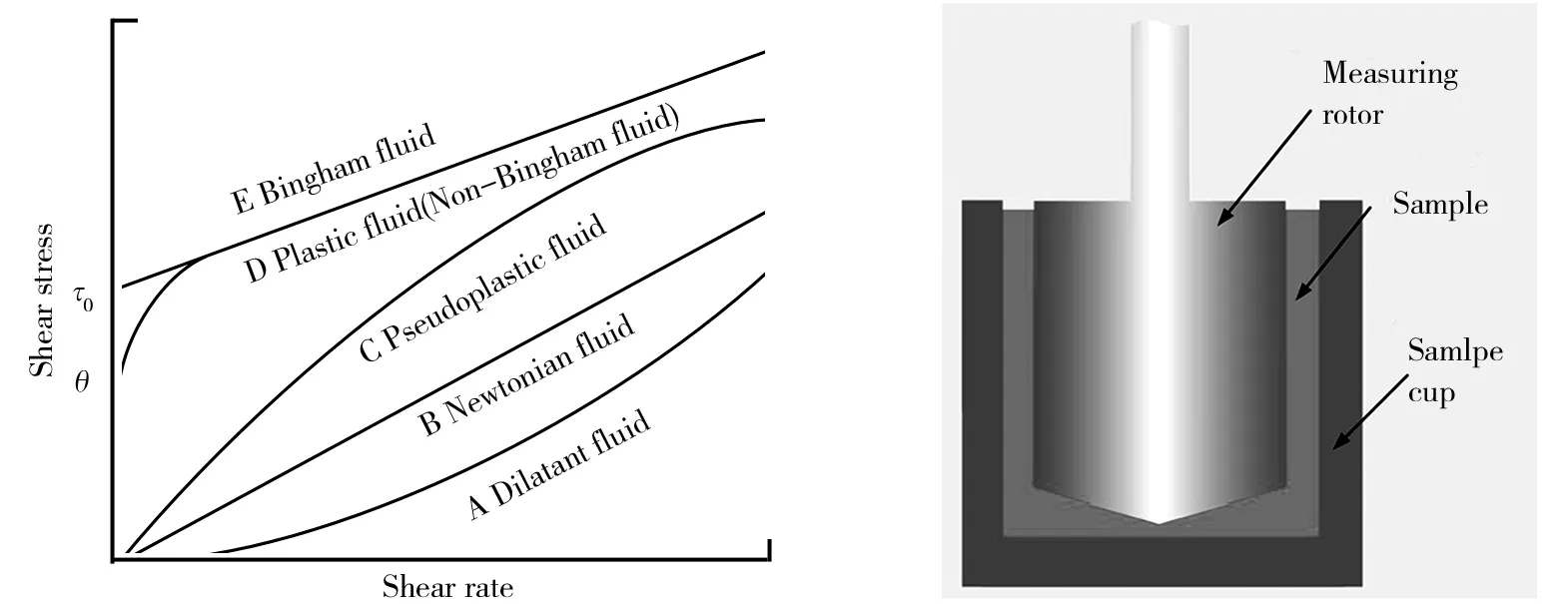
图1 各类流体的流变曲线 图2 旋转流变仪圆筒测试模块
(3)实验方法.
①流动性能测试.采用旋转流变仪的连续剪切模式,模拟润滑脂承受连续剪切的工况,剪切速率范围:0.01 s-1~100 s-1.鉴于润滑脂存在粘温特性,实验温度设置为25 ℃.
②应变扫描测试.采用旋转流变仪的振荡剪切模式,振荡频率为1 Hz,应变范围为0.1%~100%,主要考察润滑脂承受不同应变下的变化情况,以揭示其结构体系的演化规律.
③微观形貌考察.对润滑脂皂纤维结构开展,以进一步揭示其内部结构形态.实验选用德国蔡司Supera 55.场发射扫描电子显微镜(FESEM),实验测试条件:10 kV,高真空模式,放大倍数:20 000倍.测试样品制备过程中需采用有机溶剂对润滑脂进行基础油抽取[14].
2 结果与讨论
2.1 流变特性分析
润滑脂剪切应力随剪切速率的变化规律如图3所示.由图3可知,润滑脂在承受剪切过程中,剪切应力随剪切速率总体呈逐渐增大趋势.根据数据变化趋势,可分为三段(图示Ⅰ、Ⅱ和Ⅲ).Ⅰ段剪切应力随剪切速率逐渐增大;Ⅱ段剪切应力变化趋于平缓;Ⅲ段剪切应力随剪切速率又呈现逐渐增大趋势.图示变化规律与润滑脂体系的结构形态紧密相关.润滑脂为结构性的胶体分散体系结构,在承受剪切过程中存在结构强度.Ⅱ段所示的润滑脂承受剪切应力达到了其结构强度,出现了剪切屈服效应;Ⅰ段剪切应力小于其结构强度,润滑脂不流动,表现出固体的弹性特性;Ⅲ段剪切应力超过其结构强度,润滑脂展现出液体的粘性流动属性.粘性流动区域为流体稳定连续流动区域,其内的流动曲线即属于流变曲线进行流变模型定量表征的区域[9].
严锐[7]在开展泡沫混凝土流变特性的研究过程中,发现泡沫混凝土的流变特性符合H-B流变模型.周杨[15]在研究自密实混凝土流变特性时也选用了H-B流变模型.可以发现,混凝土在承受剪切过程中展现出与润滑脂类似的流动变化规律.流变模型的流变参数是流体属性定量表征的指标参数.为此,进一步开展流变模型(本构方程)和流变参数的探究.
2.2 数据拟合及均匀性评价方法
润滑脂和混凝土的粘性流动过程均符合H-B流变模型,因此选用H-B方程作为流变本构方程开展研究.H-B流变模型反应了流体剪切应力与剪切速率之间的定量数学关系.流变参数(τ,k,n)是H-B流变模型中的常数.流变参数确定,H-B流变模型将会唯一确定.对润滑脂流变曲线的粘性流动区域的流变数据采用数据拟合的方法进行分析.
采用H-B流变模型对润滑脂流变曲线进行数据拟合的结果如图4所示.由图4可知,H-B流变模型能够对流变数据进行非常好的拟合.流变参数的具体数值,即H-B模型与流变数据拟合的流变参数值及相关系数如表2所示.从图4可以看出,流变模型与流变数据展现出相当高的相关性,能够对润滑脂的粘性流动进行较好的定量表征.
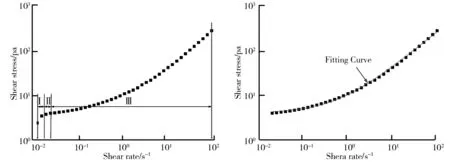
图3 剪切应力随剪切速率的变化规律 图4 实验数据与拟合曲线对比图

屈服应力τ0/Pa稠度因子k/Pa·sn剪切变稀指数n 相关系数Rxy4.056.400.8020.998
由此可见,采用流变模型与材料的流变模型进行拟合得出其流变数据,对应稳定的混合体系而言,其流变本构方程是确定的.因此,在材料的混合体系均匀性评价过程中,在混合体系内不同位置取多组样品进行流变特性测试,并开展流变本构方程的数据拟合.通过探究其流变参数的一致性,进而评价混合体系的均匀性效果.
为了进一步分析该方法的可行性,拟对材料开展进一步的性能分析.从混合体系结构角度考察其性能变化规律,揭示结构特征与流变参数之间的关联性.
2.3 结构特征及变化机理探究
润滑脂皂纤维的微观形貌如图5所示.由于润滑脂为胶体分散体系,无法通过扫描电镜对其结构进行直接考察,需采用有机溶剂抽取胶体分散体系内部的基础油.通过扫描电镜看到的实际是润滑脂皂纤维的结构骨架.通过图5可以看出,皂纤维结构骨架为高度缠结形态.润滑脂制备过程中,经加温搅拌完成皂化反应,进一步通过辊轮研磨均化,达到较为稳定的胶体体系.这也是润滑脂能够进行流变测试,在一定条件下能够得到确定流变参数的保证.
润滑脂的这种皂纤维结构使得润滑脂胶体状态的混合体系在承受剪切的过程表现出特有的流变学规律.润滑脂动态应变扫描结果如图6所示.图6中展现了润滑脂在承受不同应变过程中的储能模量和损耗模量变化规律.由图6可知,润滑脂在承受较小应变扫描过程中,储能模量和损耗模量均维持一个相对稳定值,在这样的应变范围内,润滑脂并没有流动,展现了固体的弹性特性,而随着剪切应变的增大,储能模量和损耗模量相互接近,并最终交叉.这表明润滑脂在这样的应变过程中,已经从弹性变化过程转变成粘性流动过程.应变扫描结果展现出的变化规律也印证了润滑脂流动性能测试过程中润滑脂流动展现出的三个不同阶段展现出来的规律.

图5 润滑脂皂纤维微观形貌 图6 动态应变扫描
由此可见,作为混合体系的润滑脂之所以表现出特有流变特性,与其结构特性是密不可分的.而其结构特性也是其能够展现出稳定流变特性变化规律的保证.因此,证明了基于流变本构方程进行搅拌混合塑性流体均质评价的可行性.同时,开展润滑脂流变特性测试是采用物理剪切方式模拟润滑脂承受剪切,并没有对结构体系进行破坏,展现出较为明显的优势.
3 结论
搅拌混合体系的流变特性可以采用流变本构方程进行较好的表征,流变参数与体系的性能具有较好的对应性,可以借助流变本构方程进行体系性能表征;在混合体系制备过程中,在不同位置取样,开展流变测试,采用数据拟合方法得出其流变参数,对比不同位置样品流变参数是否一致,以此判定搅拌混合体系的均匀性;作为一种物理测试方法不会对体系组成产生破坏,模拟了搅拌混合体系承受剪切过程,探究其流变特性变化规律,为一种直接测量及表征方法,具有操作简便、贴近实际工况的优势.

