租赁设备周期预防维护策略优化研究
董 克,陈圆圆
(1.安徽广播电视大学 经济与管理学院 合肥 230022;2.安徽广播电视大学 教育科学学院,合肥 230022)
近年来,市场竞争愈加激烈,企业的利润率呈下降趋势。然而,企业的设备维护成本在总成本中所占的比重越来越大[1]。自20世纪90年代以来,更多的企业倾向于租赁设备从事生产活动,代替以往自己购置设备的方式。因此,租赁设备的维护问题已逐渐成为学者和企业研究的热点问题。
当前,关于租赁设备的维护活动主要有事后维修和预防维护两种[2-3]。在实际生产过程中,小修是最常用的维修方法[4]。已有文献关于设备维护优化方面的研究,主要分为如下三类:(1) 顺序预防维护策略模型。Lin等提出了期望总成本率最小化的混合故障率顺序预防维护策略模型[5];Lin等还提出了考虑两种故障模型的混合故障率顺序维护策略模型[6];文献[7]考虑了对二手产品进行升级,并在可靠性达到限制时对二手产品进行预防维护策略模型;Sidibe等研究了在无限时间窗内的初始年龄不确定的二手产品顺序预防维护问题[8]。其他关于顺序预防维护方面的研究,可参考文献[9-12]。(2) 周期预防维护模型。Pongpech等研究了带有惩罚成本和维修时间限制的出租方维护成本最小化的周期维护策略[13];Yeh和Chen提出了基于故障率为Weibull公布的租赁设备周期预防维护策略模型[14];董克等基于设备的历史故障数据信息,提出了周期预防维护策略模型,研究了考虑设备的租赁延迟的周期维护策略[15-18]。(3)顺序维护与周期维护相结合的预防维护模型。金琳等研究了以出租方成本最小化为目标的等周期与变周期相结合的多阶段预防维护策略模型[19];Zhou等研究了周期与顺序相结合的租赁设备多阶段维护策略模型[20]。
已有关于设备维护策略方面的研究,预防维护成本主要为常数和线性两种形式。但是,在实际应用中,预防维护成本可能为多种形式。针对此问题,本文提出一种预防维护成本为非线性形式的策略模型,该模型与已有研究的区别在于:(1) 考虑了预防维护成本的非线性形式;(2) 给出了具体的寻找出租方成本最小的优化算法;(3)当预防维护成本函数中的参数c取值为零时,模型退化为线性情形,文献[13]所述情形则为本文所述模型的一个特例。最后,案例研究表明该方法的有效性,并对模型中参数灵敏度进行了分析,研究结果可为出租方进行设备维护决策提供理论依据。
一、问题描述
在设备的租赁过程中,主要涉及三个因素:出租方、承租方和合同。作为出租方,通过设备的租赁而获得租金收益,但是同时要负责对设备进行维护。作为承租方,在付出了租金以后,将会获得设备在租赁期限内的使用权。如果在租赁期内,设备发生故障停机,将会给承租方的生产经营活动带来一定的损失。因此,在租赁合同中还包含了对出租方的惩罚条款,来弥补设备发生故障停机给承租方可能带来的经济损失。文中主要研究了如下两类惩罚成本:
惩罚成本1:在租赁期L内,当设备小修时间Y在规定的时间τ之外时,将产生惩罚成本(Y-τ)Ct。当维修时间Y在规定时间τ之内时,将不产生惩罚成本。
惩罚成本2:在租赁期L内,每一次故障的发生将会产生故障惩罚成本。
从出租方的视角而言,设备故障将会产生惩罚成本,同时故障维修亦将会产生一定的成本。若对设备采取预防维护,在产生预防维护成本的同时,将会使得设备的故障维修成本以及故障惩罚成本减少。如何在它们之间做出权衡,以获得出租方期望总成本的最优值,是学者们和出租方最关心的问题,亦是本文将要研究的主要问题。
二、数学模型
模型假设:
(1)故障强度函数为λ0(t),且是关于时间t的增函数;
(2)当租赁设备发生故障时,对设备进行小修,使得设备“恢复如旧”,小修不改变设备的故障强度;
(3) 设备预防维护时间忽略不计;
(4)设备租赁期限为L。
(一)预防维护成本和故障小修成本
若出租方在等周期时间T时,对租赁设备进行预防维护,则在租赁期限L内的预防维护次数k的值为:

(1)

预防维护时间节点为tj(tj=T,2T,…,kT),第j次预防维护活动,使得租赁设备的故障强度减少δj,其中δj满足:
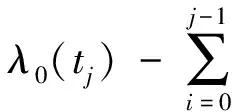
(2)
由式(2)可知,在进行周期预防维护后,故障强度函数可表示为如下形式:
(3)
其中:t0=0,δ0=0。
在租赁期限L内,若不考虑预防维护,则设备的期望故障次数为
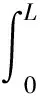
(4)
若考虑到进行预防维护,则设备的期望故障次数为
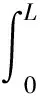
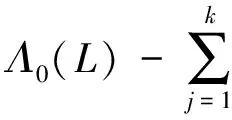
(5)
租赁设备的预防维护成本表达式为:Cp(δ)=a+bδ+cδ2(a,b,c>0),由固定成本和可变成本两部分组成。
则在租赁期限L内,预防维护成本为
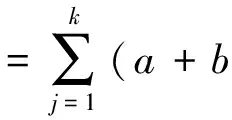
(6)
若在租赁期L内,对租赁设备实施预防维护活动后,它的故障小修期望总成本为:
TCf=CfΛ(L)。
(7)
(二)惩罚成本
在租赁期间,当设备发生故障时,将对承租方的生产经营活动产生一定程度的影响。此时,承租方将对出租方做出相应的惩罚,包括惩罚成本1和惩罚成本2。
令Y表示设备发生故障后的小修维修时间,则由式(5)可得,期望惩罚成本1为:
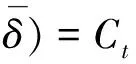
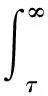
(8)
期望惩罚成本2为:

(9)
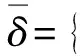
从式(6),(7),(8)和(9),可得出租方在租赁期[0,L]内,共执行k次周期预防维护活动的期望总成本为:
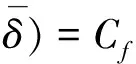
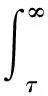
(10)

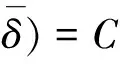
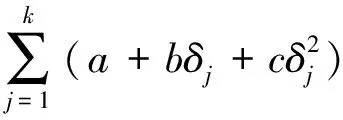
(11)
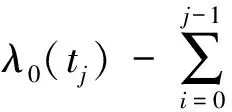
期望总成本的最优值问题,即为寻找式(11)的最优值问题。下面将对式(11)的期望总成本函数进行优化,以期获得出租方的期望总成本的最优值。
三、最优周期预防维护策略
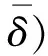
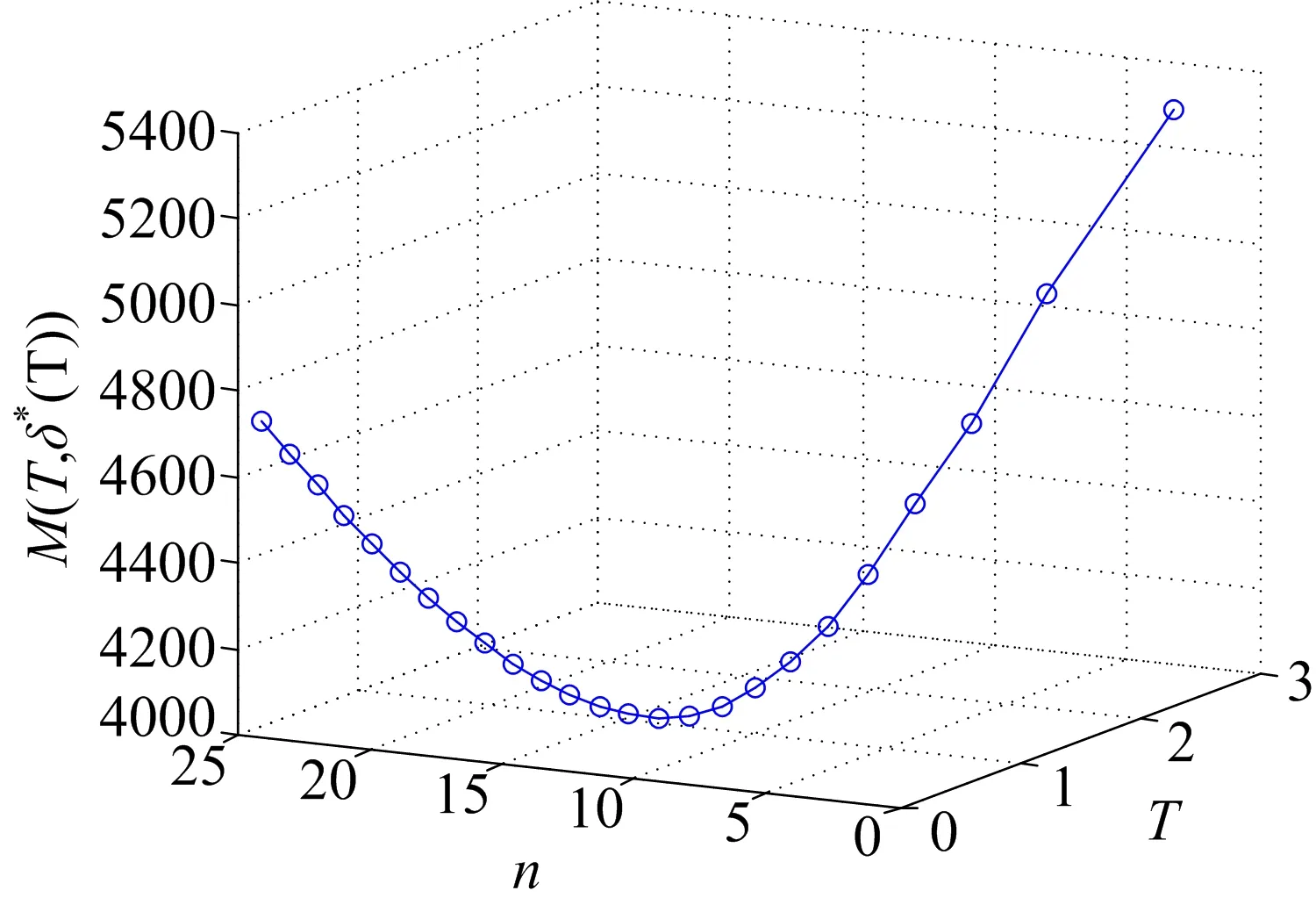
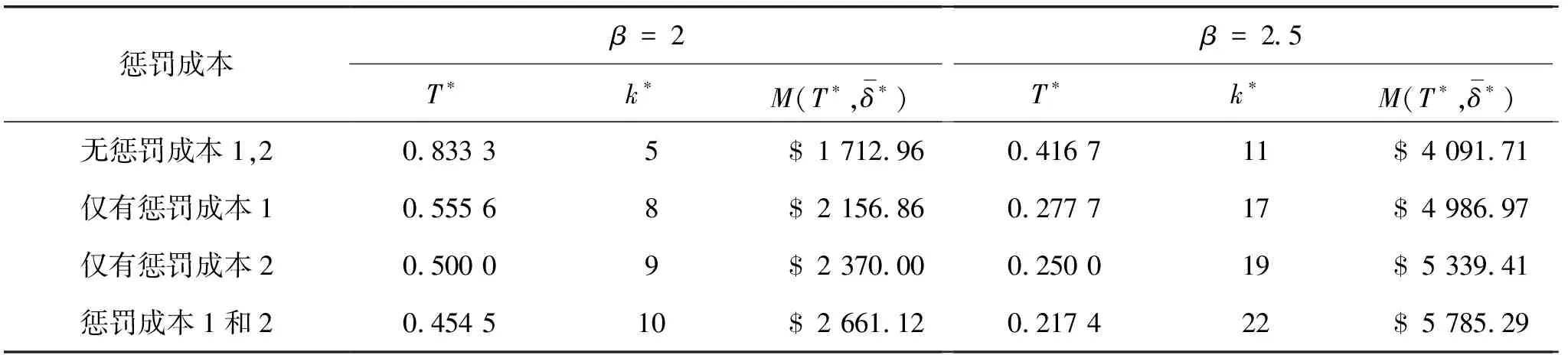
第一步:固定T,k(T)T (12) (13) 算法步骤: Step 1:初始化:k=1; Step 2:估计Tmin=L/(k+1),Tmax=L/k的值; Step 4:k←k+1。 Else执行 step 5。 假定出租方对某型号打印设备进行租赁,并且拟用上述文中所提出的维护方法对设备进行维护。假设打印设备被维护主要部件的故障率分布服从二参数的Weibull分布: , (14) 其中,α、β分别为尺度参数和形状参数。参数α、β的值可以根据设备运行的历史故障数据,利用最大似然估计方法得出[21-22]。 假定租赁设备的维修时间服从二参数的Weibull分布: ,0≤y<∞。 (15) 参数的取值如下:L=5(年),Cf=100 ($),Ct=300 ($),Cn=200 ($),τ=2 (天),m=0.5,φ=0.5,a=100 ($),b=50 ($),c=30 ($)。 表1 k取不同值时得到的T*(k)和M(T*(k), 图1 当β=2时,k取不同值时,对应的T和M(T, 图2 当β=2.5时,k取不同值时,对应的T和M(T, 在表2中,给出了当形状参数β分别取2和2.5时最优期望总成本取值及相应的参数取值。考虑了四种情形:(1) 无惩罚成本1和2;(2) 仅有惩罚成本1;(3) 仅有惩罚成本2;(4) 惩罚成本1和2都存在的情形。从表2中可以得出,当β=2时,情形(2)比情形(1)的期望总成本增加,并且最优维修时间间隔期T*变短。情形(3)与情形(2)相似,并且情形(3)时的期望总成本值增加。情形(4),维修次数增加,维修时间间隔期T*比情形(2)、(3)时变得更小,同时期望总成本亦增加。当β=2.5时,情况与上述类似,并且预防维护活动变得比β=2更频繁,因为故障强度变大。 表2 惩罚成本对最优策略的影响 文中提出了预防维护成本为非线性形式的预防维护策略模型,并给出了具体的优化算法,应用此算法,可以得到出租方所期望的最优总成本及对应的维护策略。且当参数c=0时,预防维护成本函数退化为线性形式,即为文献[13]中所研究的情形。然而在实际维护过程中,设备的故障强度不仅会随着设备的年龄增加而增大,而且会随着使用强度的增加而变化,如何考虑这些因素对设备维护成本的影响,将是未来进一步的研究方向。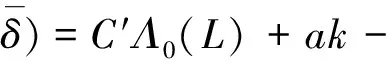
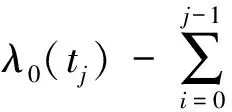
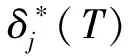
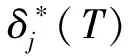
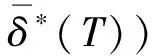
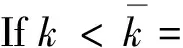
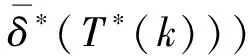
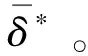
四、算例分析
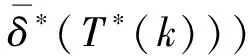



五、结论

