黏声介质全三维双平方根方程叠前深度偏移及其在海上数据中的应用

赫建伟 邓 勇 任 婷 黎孝璋 张文祥 鲁统祥

(中海油海南能源有限公司，海南海口 570100)

1 引言

常规海上拖缆地震数据采集的特点是拖缆较长且缆数相对较少。与陆上宽方位地震数据采集相比，其数据的方位覆盖通常较窄。为了实现宽方位观测，通常采用炮船和检波船分离并协同作业的方式进行数据采集。依据不同的作业方式，可实现螺旋观测系统或四船螺旋观测系统等宽方位/高密度观测[1-3]。尽管观测方位覆盖存在较大差异，宽方位和窄方位地震数据存在一个共同的特点，即炮数较多。如果按单炮道集为数据单元进行波动方程叠前深度偏移(PSDM)，即便对于当今的大规模、高性能计算机来说也是较大的挑战。

另外，随着勘探目标的埋深逐渐增大，衰减效应成为中深层地震高精度勘探不可忽略的因素。为了补偿介质的非弹性衰减，品质因子估计和衰减补偿尤为关键。品质因子估计是衰减补偿的基础，它通常由基于信号分析[4-7]和层析成像的方法获取[8]，两种方法在多个地质目标勘探中取得了不错的效果。反Q滤波[9，10]和衰减补偿偏移方法[11-17]是两种主要补偿方式。由于反Q滤波通常在单道上实现，不便于考虑复杂介质中的地震波传播，它较为适合地质结构相对简单的区域。在复杂介质中，衰减补偿的偏移方法沿着地震波传播路径来实现，其补偿方式能更好地遵循地震波传播规律。

波动方程叠前深度偏移，具有成像精度高、波形特征保持好等优点，尤其适用于精细地震勘探的成像。根据所用的波场外推算子，可分为单程波方程和双程波方程PSDM。前者又分为适用于炮集的单平方根算子PSDM和适用于CMP集的双平方根算子PSDM[18]。

单平方根算子炮域叠前深度偏移把炮点和检波点分别向下外推[19]，考虑到波可能来自于一个炮集最大炮检距覆盖的范围之外，无论炮点或是检波点向下外推，都需要扩展一定的边道，使得计算量加大。另外扩展的道数也不一定是合适的，因为地下构造千变万化而且未知。单平方根算子炮域叠前深度偏移在炮点向下外推时需要人为地给出一个子波作为震源函数，该函数的形态直接影响偏移成像效果。但震源子波提取在地震资料处理过程中一直是一个难题。单平方根算子炮域叠前深度偏移的优势是，所有能用来描述波在复杂介质中传播的算子均可用于外推成像过程中，另一个明显的优势是对野外观测方式的适应性强，仅要求单炮道集是规则的。

双平方根算子中点—半炮检距域叠前深度偏移是把炮点和检波点同时向下外推，无论对何种道集进行偏移，每一个道集均基本覆盖整个成像范围，因此不需要考虑偏移孔径问题[20]。完整意义上的双平方根算子中点—炮检距域叠前深度偏移是一个典型的五维问题，每一外推步骤都涉及三维探区的所有叠前数据，需要每个节点有相当大的内存，计算过程中需要反复调用高维快速Fourier变换(FFT)。但是，它总体计算效率高，没有偏移孔径效应，可方便地产生方位角度道集用于后续的偏移速度分析或层析成像等，因此非常适用于海上拖缆数据的叠前深度偏移成像[18]。另外，由于全三维双平方根方程PSDM是在频率域实现的，可便利地引入各种衰减模型，实现振幅衰减补偿和相位频散校正。

本文从双平方根波场外推方程导出中点—半炮检距域分步Fourier外推算子，然后将该算子推广到黏声介质，实现了中点—半炮检距域黏声叠前深度偏移方法。应用理论二维黏声介质模型数据的成像结果证明了方法的正确性； 将本文方法用于衰减现象比较普遍的中国莺歌海实际地震数据成像，取得了明显的效果。

2 中点—半炮检距域波动方程叠前深度偏移成像方法

在横向变速情况下，双平方根波场外推方程[18，19]为

(1)

式中：xs=(xs，ys)、xg=(xg，yg)分别为炮点和检波点坐标。利用坐标变换

(2)

把式(1)从炮点—检波点坐标系(xs，xg)变换到中点—半炮检距坐标系(M，H)。坐标变换的微分关系为

(3)

将式(3)代入式(1)，有

(4)

对式(4)中的慢度场(速度场的倒数)进行分解，每一外推层中的慢度分为背景慢度和慢度扰动量。在一个外推层内背景慢度是常数，为每一层慢度的平均值。定义

(5)

式中：s(M-H,z)和s(M+H,z)分别为炮点和检波点对应的慢度值；s0(z)为背景慢度；Δs(M-H,z)和Δs(M+H,z)分别为炮点和检波点处的慢度扰动。炮点与检波点的背景慢度是相同的，而两点的慢度扰动量不同。把定义的慢度分解式(5)代入式(4)，并舍弃慢度扰动的二阶项，可得

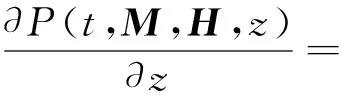
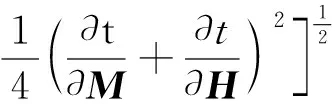
(6)

可重写为

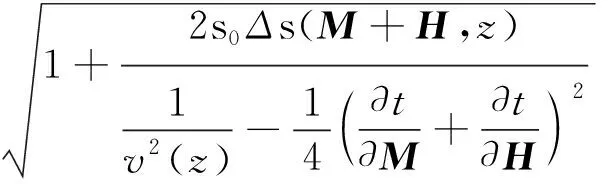
(7)

对式(7)中的根式作Taylor展开，并舍弃二阶以上项，可得

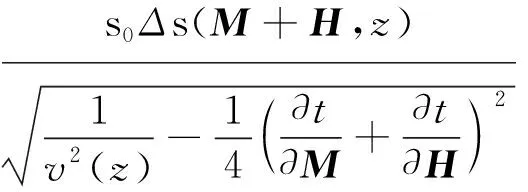
(8)

整理为

(9)

将式(9)变换到频率波数域，为

(10)

式中

对式(10)进行分解，可得

(11)

其中： 式(11a)是背景介质中的波场外推方程，它是一个双平方根算子相移偏移方程； 式(11b)描述慢度扰动引起的散射场。背景场与散射场之和构成总场。

事实上，式(11)是广义屏方法在中点—半炮检距域中的波场外推公式。在窄传播角情况下，k0/kz≈1成立，可得到裂步Fourier偏移方法[21，22]。考虑宽传播角时，可导出广义屏偏移方法[23，24]。在仅考虑窄传播角的情况时，式(11b)可最终简化为

(12)

式(11a)和式(12)结合在一起，就是裂步Fourier方法在中点—半炮检距域中的波场外推方程。

在中点—半炮检距道集中，用双平方根算子把激发点和接收点同时向下外推进行波动方程叠前深度偏移。外推及成像公式为

P(t=0,Km,H=0,z+Δz)

P(ω,Km,Kh,z)

(13)

式中

(14)

上述三维偏移是在五维空间中进行的，它是全三维PSDM，使用一个进程读取所有的观测数据，即使在频率域对单个频率的数据进行全三维PSDM，也需要单个计算节点有较大的内存(比如128G)。随着计算设备性能的提升，这一要求能逐渐得到满足。

3 黏声介质全三维双平方根方程叠前深度偏移

全三维双平方根方程PSDM由于在频率域实现，可便利地把各种吸收衰减模型引入成像过程。

黏声介质中双平方根算子(DSR)有如下频散关系

(15)

式中kω为复波数。

黏声方程和声波方程的DSR频散关系在形式上是类似的，只是黏声方程中引入了复波数来考虑介质的吸收衰减。因此，在推导波场外推算子时可采用类似声波方程的推导步骤，最终得到与式(13)形式类似的波场外推算子。对介质的吸收衰减补偿分为对背景场和对扰动场的补偿。本文仅对背景场进行补偿，可达到提高中深层成像质量的目的。当然，也可融入对扰动场的补偿，来更好地实现衰减补偿。

选用Kjartansson模型[25，26]描述地下介质的吸收衰减机制。复波数kω可以表示为

(16)

式中

(17)

其中：ω0为参考频率，一般选取地震资料主频；α为振幅衰减系数；Q为黏声介质的品质因子；vr为声介质中地震波传播速度；vP为吸收引起的频散相速度。

式(16)在一定的假设下描述了介质的衰减效应。偏移成像的过程中，为了补偿吸收掉能量，α前面取正号，就可以有效地补偿中深层的反射能量。

因此，式(15)中的相移因子变为

(18)

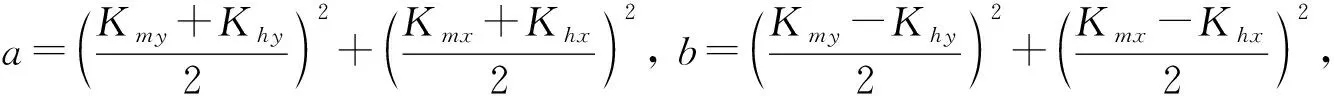
P(H,M;z+Δz)=P(H,M;z)exp(-iΔzkz)

(19)

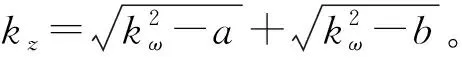
进一步地，定义

(20)

根式中的实部控制地震波的传播，校正频散; 虚部用于补偿衰减的能量。

从双平方根算子的波传播角度考虑，炮、检点同时向下外推，双程路径都应补偿能量的衰减。此时，只要虚部保证取正值，就可以实现在整个波场传播路径上进行振幅补偿。

在黏声介质中进行偏移成像时，由于波场振幅在深度域外推过程中呈指数关系增长，所以计算过程可能出现不稳定现象，本文采用增益截频法保障稳定性。增益截频的定义为[27,28]

(21)

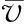
可利用Aki等[29]提出的公式计算L

(22)

式中：A0为地震波的初始振幅；A为地震波在偏移深度上的振幅。式(22)中，通过控制的初始振幅和偏移深度上的振幅的比例(即控制偏移过程中增幅增大的程度)，即可算出振幅增长控制系数。

4 数值试验

4.1 模型数据试验

由于目前没有较好的三维黏滞衰减介质模型，采用二维复杂岩性模型测试吸收衰减补偿的有效性。该模型采用黏弹波动方程正演，用其垂直分量作为纵波波场。图1为模型的速度场和品质因子，用每一层的品质因子平均值作为背景场补偿的品质因子。图2a为声波双平方根方程PSDM结果，图2b 为黏声双平方根方程PSDM结果。图3为图2的局部放大，可以看出，虽然声波偏移对整个构造形态能够较好地成像，但是模型数据是利用黏弹波动方程进行正演的，因此声波偏移结果的中深层的成像质量不好，主要是因为中深层的能量很弱。而黏声偏移在整个波路径上进行了能量补偿和相位校正，因此在偏移结果中深层的能量得到显著提高，分辨率得到一定提升。

图1 速度模型(a)和品质因子模型(b)

4.2 实际三维数据试验

为了进一步检验方法的有效性，利用莺歌海盆地实际资料进行试验。图4和图5分别为该资料利用声介质和黏声介质双平方根方程叠前深度成像的结果。对比图4与图5可以看出，经过衰减补偿，成像振幅得到了较好的恢复，深层成像能量变强。同时，由于在成像过程中进行了相位补偿，成像聚焦性也得到一定的改善。在深度3500～4000m之间的倾斜构造聚焦性明显提升；在深度4000～4500m之间聚焦性改善较大，构造形态更加清晰，利于后续的解释工作。这表明该方法可较好地应用于实际数据处理。

图2 模型数据声波方程(a)与黏声方程(b)PSDM结果

图3 声波方程(a)与黏声方程(b)PSDM结果的局部放大

4.3 计算效率分析

以窄方位3D SEG/EAGE盐丘模型为例，说明全三维PSDM与逆时偏移(RTM)的计算效率。RTM在炮域实现，用时为38248min。将共炮数据变换到CMP域进行基于双平方根方程的全三维PSDM，用时为1548min。两种偏移方法所用参数如表1所示。由此可知，与RTM相比，CMP域的全三维PSDM具有明显的效率优势，比较适合炮数较多的海上高密度采集。

表1 窄方位3D SEG/EAGE模型主要偏移参数

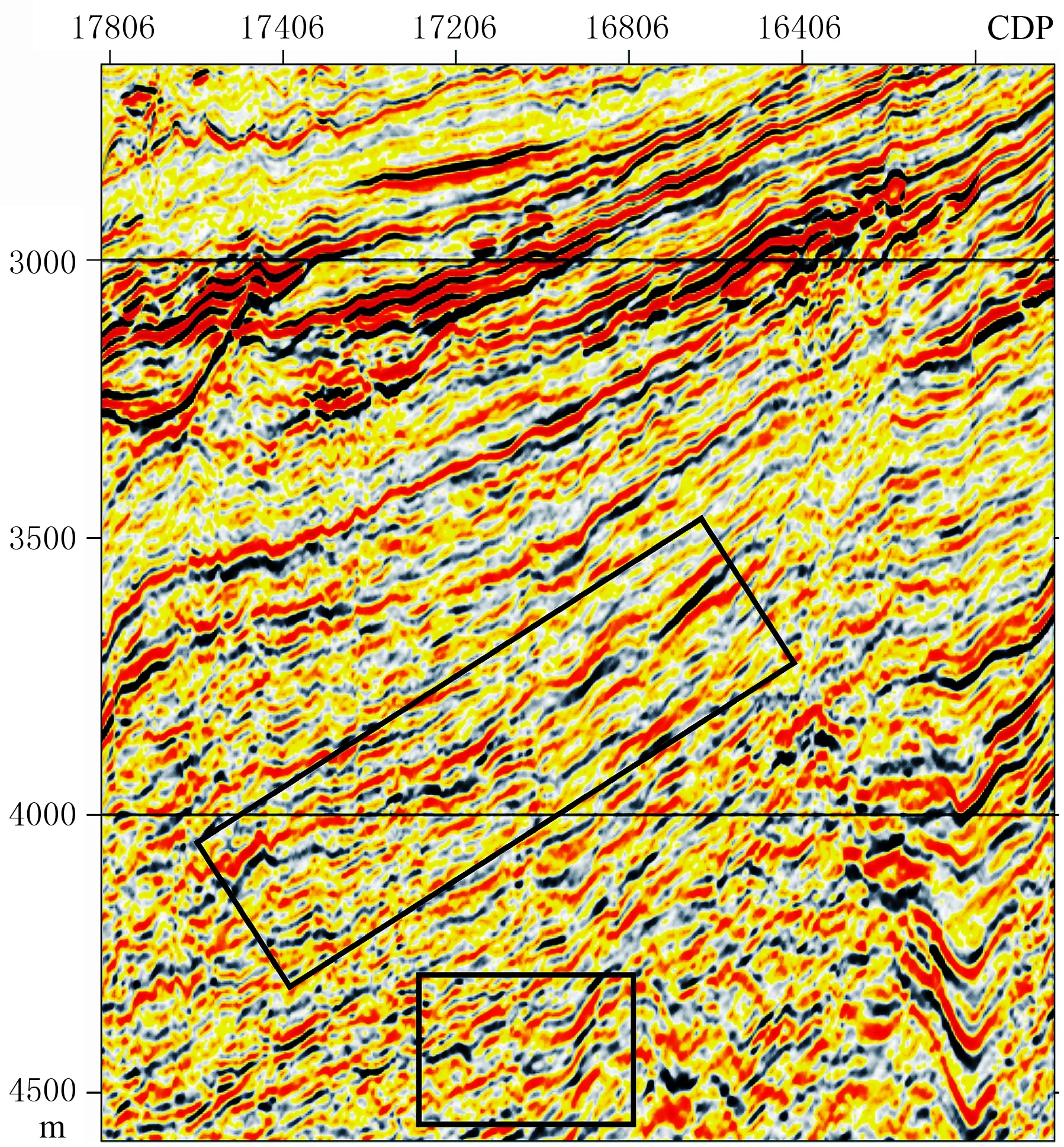
图4 实际资料声波双平方根方程PSDM剖面

图5 实际资料黏声介质双平方根方程PSDM剖面

5 结论

针对海量炮数的海上地震数据，发展了一种基于双平方根算子的黏声介质全三维叠前深度偏移方法。在基于双平方根算子的声介质波场外推和成像公式推导的基础上，在背景场波场外推过程中，引入衰减补偿，校正介质的非弹性吸收对地震波造成的相位畸变和能量衰减。同时，将增益截频方法引入波场外推过程中，保障方法的稳定性。模型和海上实际数据的测试结果表明，通过对介质非弹性衰减进行补偿，偏移结果的分辨率得到了一定提高；中深层的弱信号能量得到较好恢复；成像聚焦性得到一定改善，构造形态更为清楚。

本文研究得到同济大学王华忠教授及中海油湛江分公司李列、周家雄等专家的支持，在此表示衷心的感谢。