云南松林分平均胸径生长模型及模型参数环境解释

罗恒春，张 超，魏安超，张 一，黄 田，余哲修

（西南林业大学 林学院，云南 昆明 650224）

在林木生长过程中，随着林分年龄的变化而表现出来的规律称为林木生长规律，根据此规律所构建的模型称作森林生长模型。国外林业发达国家在18世纪就开展了对森林生长量和收获量的相关研究［1－2］。1721年德国REAUMUR首次提出了收获表的概念，引起了林学界相关学者的重视［3］；之后便出现针对森林生长模型的研究，在此基础上，许多国家在建立森林资源连续监测固定样地的同时，提出了适合本国的森林生长模型［4－5］。到了20世纪中叶，伴随着计算机及网络技术的发展，开始建立复杂的数学方程，并利用计算机技术来模拟单木生长模型，该模型考虑了林木之间存在的空间距离以及竞争关系；林分生长模型的概念被提出是在1987年召开的全球林分生长模型和模拟的会议上［6］。中国对森林生长模型方面的研究起步相对较晚，直到20世纪末期，才相继出现了几个重要的林分生长模型。唐守正等［7］依据模型的层次以及预估结果将林分生长模型划分为3类：以林分总体特征指标变量为基础的全林分模型，以林木级为基本模拟单元的径阶分布模型以及以单木生长信息为基础的单木生长模型。胥辉［8］构建了思茅松Pinus kesiyavar.langbianensis天然次生林林分的生长模型系统。陈建新等［9］采用Logistic模型模拟了树高、胸径以及材积生长进程曲线，最终确定材积、胸径和树高的速生期分别为13.64，12.77和11.27 a。田新辉等［10］在研究林分密度对107杨Populus×euramericana‘Neva’人工林的影响时发现，林分胸径、树高及单株材积等林分生长因子均随林分密度的增加而逐渐减小，而高径比随密度增加而上升，林分蓄积量随密度的增加呈抛物线变化。郑小贤［11］从单木生长和林分平均生长2个水平上研究了信州落叶松Larix gmelinii林生长及其相互关系，并建立了林分整体生长模型和预测系统。混合效应模型最早研究于20世纪70年代，是在模型中考虑了固定效应和随机效应，按形式分为线性混合效应和非线性混合效应。在中国林业上也有广泛的应用，且有不少研究对混合效应模型的拟合方法进行了总结［12－13］，王明初等［14］基于混合效应模型及经验线性无偏最优预测法（EBLUP）对杉木Cunninghamia lanceolata树高生长过程进行了预测，取得了较好的拟合精度；高慧淋等［15］利用混合效应模型的固定效应部分对人工落叶松解析木的内部和外部轮廓进行模拟。森林与环境之间存在着密不可分的联系，相互影响的同时相互制约，最终形成一个复杂的整体。环境中对森林有影响的环境因素便称为森林生态因子，根据性质可分为气候因子、地形因子及土壤因子等。环境影响因子对森林的影响表现在多方面，森林的生长受气温、降水及湿度等气候因子的影响［16］。高洪娜等［17］研究表明：树木的年轮生长与生长季的温度之间存在较为复杂的关系，与降水之间却存在较为明确的正相关关系。曹受金［18］对不同松科Pinaceae树种的研究表明，气候因子与不同树种的径向生长间的相关性不同，幼龄林的树木对生长季的气温和降水有着显著的响应，但过熟林的林木受生长季末气候的影响极为显著。梁诗博［19］在建立林分生长的过程模型基础上，考虑环境因子对林分生产的干扰，建立了环境因子模型。目前，已有诸多学者对云南松Pinus yunnanensis的生长模型进行了研究，但结合气候因子的研究仍鲜见报道。本研究结合基本理论生长模型，采用非线性回归模型方法，构建云南松林分平均胸径生长模型，在选出的最优模型的不同参数组合位置上引入环境因子，进行模型参数环境解释，有助于了解气候变化对云南松林分生长的影响，旨在为云南松林可持续经营提供经验基础模型。

1 数据来源及处理

样地数据来源于1987－2007年云南省森林资源连续清查样地数据（第3～7次）。据云南省地貌特点及森林分布情况，在全省范围内采用系统抽样方法，抽样间距为6 km×8 km，设置方形实测样地，样地面积为0.08 hm2。其中，研究中所使用林分平均胸径和平均年龄均是按照森林资源连续清查的标准进行计算而得到。气象数据来源于1987－2007年云南省境内35个国家一、二级地面气象自动站逐日观测数据，包括气温、降水量、相对湿度、日照时数以及地表风速。

对样地数据和气象数据进行以下处理：①基于5期一类清查样地数据，以滇中地区（昆明市、楚雄市、玉溪市和曲靖市）为研究区，筛选出5期云南松复测样地数据，为分析林分生长情况做准备，每期选出211个样地，删除一些数据不完整的样地，最终用于研究的是182个样地；②提取与连清样地调查数据的年份相对应的气象数据，通过数据透视表进行初步整理，计算出滇中地区每个站点每年对应的月均值，进一步在ArcGIS中采用空间插值的方法计算出每期各样地对应的月均值，最后计算出每期各样地所对应的气象数据年均值，即5 a的气象数据平均值，为后续分析做准备。

2 研究方法

2.1 林分生长模型构建方法

基于滇中地区随机选取的80%的云南松样地数据，结合国内外研究成果，选取如表1中的6个基础模型形式对林分平均胸径的生长进行拟合、模型评价和最优模型选择。

表1 林分生长模型Table 1 Stand growth models

2.2 模型精度检验

基于未参与建模的20%的云南松样地数据，根据精度检验要求，通过决定系数R2和均方根误差（ERMS）， 总相对误差（sum relative error，Es），平均相对误差（mean relative error，EM），绝对平均相对误差（absolute mean relative error，EA）和预估精度（predict precision，P）对模型偏差统计量进行比较，评价模型的预测能力［20］。计算公式如下：

式（1）～式（6）中：yi为实际观测值；为模型预估值；为实际值的平均值；n为样本数；ta为置信水平为a=0.05时的t分布值；T为回归模型中参数个数；为预估值的平均值，即

2.3 气象因子的选择与计算

选择代表热量、水分和水热综合的气象因子，其中：代表热量的气象因子有年平均气温（mean annual temperature，TA）， 年平均生物学温度（biological temperature，TB）， 温暖指数（warmth index，IW）； 代表水分的气象因子有年平均降水量（mean annual precipitation，PA）；代表水热综合的气象因子有潜在蒸散量（potential evapotranspiration，ET0）和湿润指数（humidity index，IH）。

温暖指数（IW）指1 a中月平均气温超过5℃的气温之和，是植物生长的热量条件。计算方法如式（7）：

式（7）中：ti为第i个月的平均气温（℃），n为对应的月份数。

年平均生物学温度（TB）是指适合植物生长范围内的年内平均气温，一般波动范围为0～30℃。气温低于0℃按0℃计算，高于30℃时按30℃计算。该指数能较好地反映植被类型与气候之间的关系适应性［21］。计算方法如式（8）：

式（8）中：TBi为大于0℃小于30℃的月平均气温；n为对应的月份数。

湿润指数（IH）是衡量气候的湿润程度，是地面水分收入量与支出量的比值，一般用年降水量与潜在蒸散量的比值表示。值越大，表明气候越湿润。计算方法如式（9）和式（10）：

式（9）～式（10）中:PA为年降水量（mm）；ET0为最大潜在蒸散量（℃·月）。 其计算公式如参考文献［22］，Rn为净辐射量；G为土壤热通量；γ为干湿计常数；T为地表高2 m处的平均气温；U2为地表高2 m处的平均风速；eS和ea分别为饱和水汽压和实际水汽压；Δ为当前气温时饱和水汽压曲线斜率。

3 结果与分析

3.1 滇中地区云南松林分平均胸径生长模型构建

基于滇中地区80%的云南松样地数据，采用表1中的基本理论生长模型对林分平均胸径进行模型拟合。由表2可知，6个基础模型的拟合结果中，除Shumacher模型的拟合决定系数（R2）在0.60以下，其他模型的拟合效果相近，均在0.62以上。其中，Gompertz模型的拟合效果最好，R2达到0.648，ERMS为3.384；Schumacher模型的拟合效果最差，R2为0.544，ERMS为3.772。基于未参与建模的20%的云南松样地数据，从总相对误差（ES），平均相对误差（EM），绝对平均相对误差（EA）和预估精度（P）等4个统计量对模型进行检验，评价模型的预估能力。具体结果如表3。

6个理论模型整体表现良好，整体检验效果比较接近。其中，总相对误差（ES）和平均相对误差（EM）是Gompertz模型表现最好；绝对平均相对误差（EA）均小于30%，Richards模型表现的最好；预估精度（P）均在95%以上，其中Gompertz模型的最高。

表2 林分平均胸径生长模型拟合结果Table 2 Fitting result of stand diameter growth model

表3 模型检验结果Table 3 Results of model testing

综合拟合指标和独立性检验指标，Logistic模型和Gompertz模型的比较最接近，但Logistic模型的性质比较适合描述生物种群的生长，而Gompertz模型的性质比较适合于描述树木生长，故最终选择拟合效果和检验结果最优的Gompertz模型作为林分平均胸径的生长模型。具体模型如式（11）。

式（11）中，A为林分平均年龄，单位为a。

3.2 滇中地区云南松林分平均胸径生长模型参数的环境解释

基于滇中地区80%的云南松样地数据，以最优的Gompertz模型为基础模型，分别引入林分特征因子海拔（ALT）， 郁闭度（CD）， 地形因子坡度（SLO）以及气象因子年平均气温（TA）， 年平均生物学温度（TB），温暖指数（IW），年平均降水量（PA）， 潜在蒸散量（ET0）和湿润指数（IH）。以决定系数（R2）与均方根误差ERMS为指标，考虑将环境影响因子（林分、地形和气候）引入不同的参数组合，具体引入位置，以引入海拔因子为例（表4），其中有2个或3个参数时，是将环境因子同时引入到2个或3个参数位置上。结合未参与建模的20%的云南松样地数据，结合总相对误差ES，平均相对误差EM，绝对平均相对误差EA和预估精度P等4个统计量对模型进行检验，最终选出拟合效果表现最优的模型，作为最佳模型形式。

表4 环境因子引入模型参数位置表Table 4 Position table of introduction of the environmental factors

3.2.1 引入环境因子后林分平均胸径生长模型构建 基于最优林分平均胸径生长模型和表4，对模型参数a，参数b和参数c的不同组合位置引入各环境影响因子。引入后对模型进行拟合，将拟合效果表现较好的2个结果汇总于表5。由表5可知：引入各环境因子后，模型的决定系数（R2）均有所提高，均方根误差 （ERMS）均有所减小，模型拟合效果明显提高。将各环境因子引入到7个不同参数组合位置上，均是引入到2个参数或3个参数位置上的表现最好。将海拔同时引入到3个参数位置时，模型拟合效果表现最好，引入到参数a，b位置上时表现次之；将坡度引入到3个参数位置时，模型拟合效果表现最好；引入到参数a，c上的表现次之；将郁闭度同时引入到参数a，c和参数a，b，c位置上时表现最好且一致；将年平均气温引入到参数a，b位置上和参数a，b，c位置上时表现最好且一致；将生物学温度引入到参数a，c位置上时表现最好，引入参数a，b，c位置上时的模型表现次之；将温暖指数引入到参数a，c和参数a，b，c位置上时表现最好且一致；将年平均降水量引入到参数a，b，c位置上时表现最好，但参数估计值为负，失去了生物学意义，故引入到参数a，b位置上时表现最好；将潜在蒸散量引入到参数a，b，c位置上时表现最好，但参数b的估计值为负，失去了生物学意义，故引入到参数a，b和参数a，c位置上时表现最好；将湿润指数引入到参数a，b，c位置时表现最好，但参数a的估计值为负，失去了生物学意义，故将湿润指数引入到参数a，b位置上时表现最好。

3.2.2 引入环境因子后林分平均胸径生长模型检验 利用未参与建模的20%样地数据，对不同参数组合位置引入各环境影响因子的模型形式进行精度检验。由表6可知：引入各环境影响因子后，均是将其同时引入到2个参数位置上时，检验指标ES，EM和RMA的估计值均小于引入到3个参数位置上，且预估精度P较大，故将环境影响因子引入到2个参数位置上时的模型作为解释环境影响因子对林分胸径生长模型的影响的最佳模型形式。不同环境影响因子的具体模型形式如式（12）～式（20）。

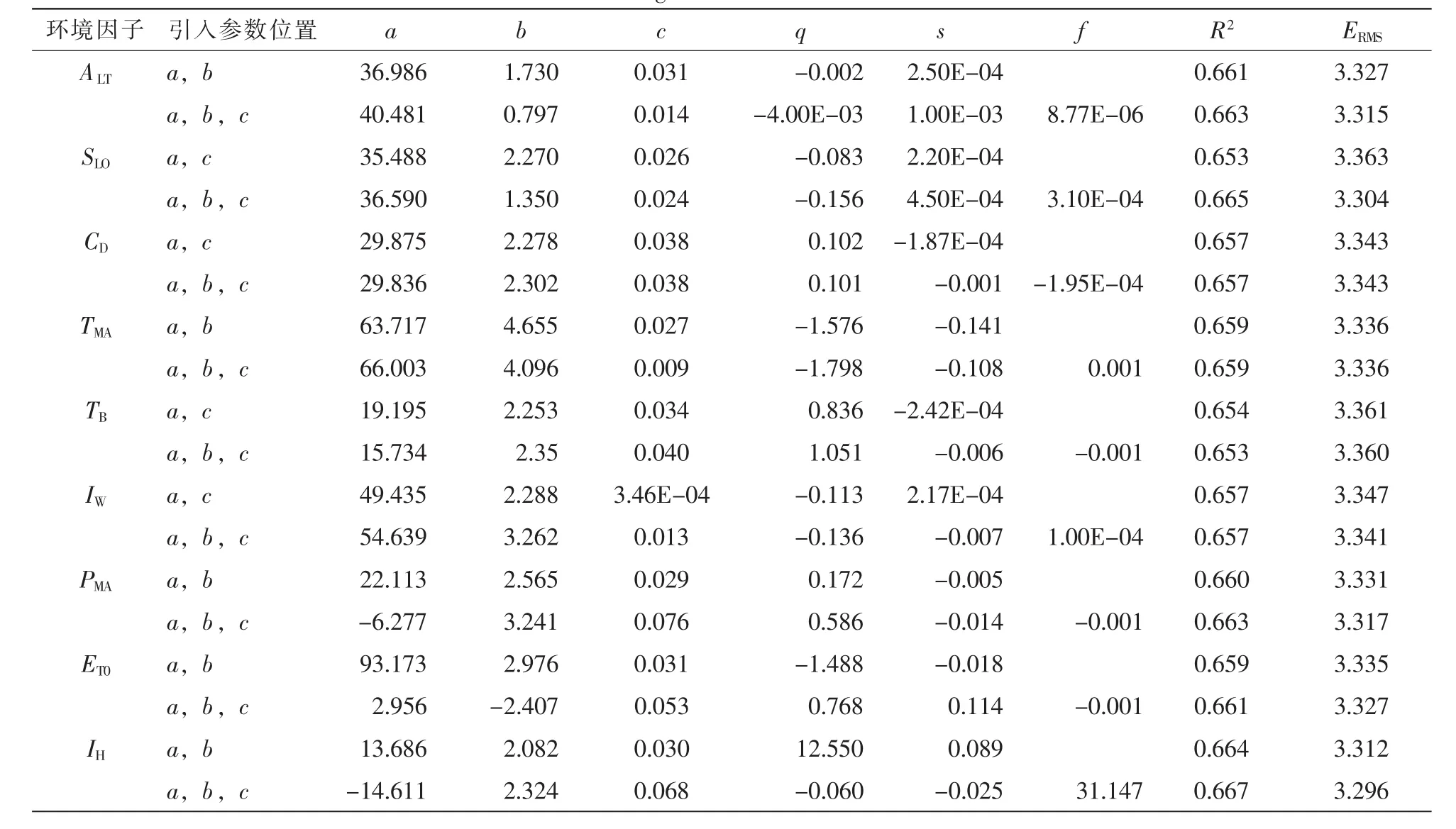
表5 引入环境因子后模型拟合结果Table 5 Results of the model fitting after the introduction of the environmental factors

表6 引入各环境因子后模型拟合检验结果Table 6 Results of the model testing after the introduction of the environmental factors

由式（12）可知，将海拔同时引入到参数a，b上的模型形式拟合效果和检验结果最优，将此作为解释海拔影响因子对林分平均胸径生长模型的影响，同时说明海拔影响了林分平均胸径生长的最大值，且模型拟合时q参数估计值为负，故林分平均胸径生长最大值与海拔呈负相关关系。

由式（13）可知，将坡度同时引入到参数a，c上的模型形式作为解释坡度对林分平均胸径生长模型的影响，同时说明坡度影响了林分平均胸径生长的最大值和生长速率，且模型拟合时q参数估计值为负，s参数估计值为正，故林分平均胸径生长最大值与坡度呈负相关关系，生长速率与坡度呈正相关关系。

由式（14）可知，将郁闭度同时引入到参数a，c上的模型形式作为解释郁闭度对林分平均胸径生长模型的影响，同时说明郁闭度影响了林分平均胸径生长的最大值和生长速率，且模型拟合时q参数估计值为正，s参数估计值为负，故林分平均胸径生长最大值与郁闭度呈正相关关系，生长速率与郁闭度呈负相关关系。

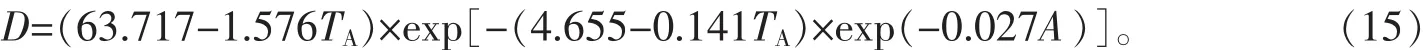
由式（15）可知，将年平均气温同时引入到参数a，b上的模型形式作为解释年平均气温对林分平均胸径生长模型的影响，同时说明年均温度影响了林分平均胸径生长的最大值，且模型拟合时q参数估计值为负，故林分平均胸径生长最大值与年平均气温呈负相关关系，年平均气温对林分平均胸径的生长速率的影响不大。

由式（16）可知，将年平均生物学温度同时引入到参数a，c上的模型形式作为解释年平均生物学温度对林分平均胸径生长模型的影响，同时说明年平均生物学温度影响了林分平均胸径生长的最大值和生长速率，且模型拟合时q参数估计值为正，s参数估计值为负，故林分平均胸径生长最大值与年均生物学温度呈正相关关系，生长速率与年均生物学温度呈负相关关系。

由式（17）可知，将温暖指数同时引入到参数a，c上的模型形式作为解释温暖指数对林分平均胸径生长模型的影响，同时说明温暖指数影响了林分平均胸径生长的最大值和生长速率，且模型拟合时q参数估计值为负，s参数估计值为正，故林分平均胸径生长最大值与温暖指数呈负相关关系，生长速率与温暖指数呈正相关关系。

由式（18）可知，将年平均降水量同时引入到参数a，b上的模型形式作为解释年均降水量对林分平均胸径生长模型的影响，同时说明年均降水量影响了林分平均胸径生长的最大值，且q参数估计值为正，故林分平均胸径生长最大值与年均降水量呈正相关关系，但年均降水量对生长速率的影响不大。

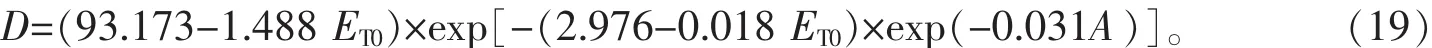
由式（19）可知，将潜在蒸散量同时引入到参数a，b上的模型形式作为解释潜在蒸散量对林分平均胸径生长模型的影响，同时说明潜在蒸散量影响了林分平均胸径生长的最大值，且模型拟合时q参数估计值为负，故林分平均胸径生长最大值与潜在蒸散量呈负相关关系，生长速率与潜在蒸散量间的关系不显著。

由式（20）可知，将湿润指数同时引入到参数a，b上的模型形式作为解释湿润指数对林分平均胸径生长模型的影响，同时说明湿润指数影响了林分平均胸径生长的最大值，且模型拟合时q参数估计值为正，故林分平均胸径生长最大值与湿润指数呈正相关关系，生长速率与湿润指数之间的关系不显著。

4 结论与讨论

基于滇中地区80%的云南松建模数据，采用6种基本理论生长模型对云南松林分平均胸径进行拟合，利用20%未参与建模的数据，对模型的独立性进行检验的结果可知，最优模型为Gompertz模型，其决定系数R2和均方根误差ERMS分别为0.648和3.384，预估精度P为96.53%。

对最优模型的不同参数位置引入环境影响因子（林分、地形和气候）进行环境解释。由结果可知：将海拔、年平均气温、年平均降水量、湿润指数和潜在蒸散量分别引入到a和b位置上，将坡度、郁闭度、年平均生物学温度、温暖指数分别引入到a和c位置上时，模型拟合结果最好，检验效果最佳。

将环境影响因子（林分、地形和气候）同时引入到2个参数位置时的模型形式表现最好，其中湿润指数对林分胸径生长模型的影响最大，海拔对其影响次之，土壤厚度对其影响最差，各环境影响因子（林分、地形和气候）对林分胸径生长模型的影响程度大小排序为IH＞ALT＞PA＞ET0＞TA＞IW＞CD＞TB＞SLO。

国内外对气候与森林生长关系的研究很多，尤其是温度已经被确定为关键性的限制因素［23］，且多数研究中得到的结论是森林生长与温度之间的相关性有正有负，研究得到的结论也一致。本研究发现：湿润指数和最大潜在蒸散量与林分平均胸径生长的关系受到降水的影响，这与臧颢［24］的研究结论相似，即温度对林分平均高生长的影响是通过对降水的制约来实现的。地形因子中海拔对林分平均胸径生长的影响不明显的结论与李兵兵［25］对林分生长规律与地形因子的关系研究结果一致。

在将每个环境影响因子（林分、地形和气候）引入到最优生长模型的不同参数组合位置上进行拟合时，发现此方法能提高模型的拟合效果和预估精度。由此可知，在对林分的生长进行拟合分析时，应考虑影响林木生长的各因子以提高模型拟合的准确度。

在对林分平均胸径生长模型参数的环境解释过程中，发现部分模型参数变动范围较大或是为负，失去了参数原本所代表的生物学意义。究其原因，参数a作为树木生长的最大参数值，与树木生长的最大值有关，研究中使用的是林分胸径平均值，因此其变动范围属正常范畴；对生长参数b的影响因素较多，故其变动范围较大亦属正常；而参数c的变动原因有待于进一步讨论。