土壤膨胀性对降雨入渗产流影响试验

邵丽媛，甘永德，苏辉东,3，贾仰文，张海涛，赵思远，郑柏杨

(1.河北工程大学水利水电学院,河北 邯郸 056000; 2.中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室,北京 100038; 3.清华大学水利水电工程系,北京 100084)

0 引 言

膨胀性土壤在全世界有广泛的分布，土壤膨胀性对工程建设、生态保护、农业种植和社会经济都有严重的破坏作用[1,2]。在自然条件下，膨胀性土壤会发生周而复始的吸水膨胀、失水干缩的干湿交替过程。由于其结构稳定性差，强烈的湿胀干缩作用产生的压力和应力的变化会使膨胀性土的受力和形态发生改变[3-5]。降雨入渗产流是水循环的重要组成部分，而土壤膨胀性会影响降水在陆面水文循环入渗过程[6,7]。土壤胀缩变化是一个复杂的过程，主要受到膨胀力和自重应力的影响。其中膨胀力的大小随土壤含水量变化而变化，自重应力会因土壤深度变化而变化，导致土壤受力变形特征会随着土壤深度的增加而发生改变，所以导致土壤水分运动参数和入渗特性等变化，使土壤入渗过程变得复杂。

非饱和带多孔介质中的土壤水分运移研究是目前研究的热点和难点，目前研究主要集中在分层土壤、空气阻力、土石混合介质等对土壤入渗产流的影响[8-11]，而有关膨胀性土降雨入渗的研究偏少。仇荣亮等[4]对变形土的膨胀收缩特点进行了研究，也表明土壤的胀缩潜力必须借助于干旱交替才得以表达，但没对膨胀性土壤入渗过程进行描述。吕殿青、邵明安等[13-15]通过实验研究，测定五种收缩特征曲线，着重描述了土壤收缩特征，只对收缩特征指标和土壤物理学特性间的关系研究。而黄传琴等[16]探讨在干湿交替过程中膨胀性土壤的胀缩特征，通过研究土壤脱水收缩和吸水膨胀过程中比容积与含水量的关系，采用三直线模型[17]拟合土壤胀缩过程，不过主要也是针对膨胀性土壤的收缩、膨胀过程进行分析。甘永德等[18,19]更是建立膨胀性土壤的土壤水分运动参数计算模型，量化了膨胀变形对入渗产生的影响，进一步提出了考虑土壤膨胀性非稳定降雨入渗产流模型(GJGAM)，拟合结果较好，但都没有针对膨胀性土壤的入渗产流过程进行描述。而刘春成等[20]对斥水土壤的入渗规律进行四种入渗模型拟合探讨其适用性；司曼菲等[21]只拟合了在土石混合介质碎石情况下土壤入渗过程，然而膨胀性介质导致的土壤参数变化、入渗曲线的影响没有研究。

基于以上研究，本文主要针对膨胀性土壤开展了室内不同厚度土壤降雨入渗产流实验以及土壤水分运动参数测定，研究分析降雨入渗条件下土壤容重变化情况，土壤累积入渗量和入渗强度随时间变化关系；并采用Philip公式、Kostiakov公式和Horton公式分别对土壤入渗过程水分运动曲线拟合。本文主要研究目的:①研究土壤膨胀性在降雨条件下对土壤参数变化的影响；②寻找最适合拟合膨胀性土壤的特征水分运动曲线的方法，能够正确描述土壤膨胀性在降雨条件下影响入渗的经验模型。相关研究可以促进对膨胀性土壤水分入渗过程的认识，丰富多孔介质土壤水运动规律。

1 试验材料与试验设计

1.1 试验材料

本次试验采用两种典型膨胀性土壤——黄绵土和娄土，这两种土壤皆是黄土高原常见的土壤，由于水土流失地表土层冲刷黄土暴露后耕种而成。其中娄土是自然褐土基础上经过人类长期耕作熟化的耕作土壤，主要分布于陕西关中盆地及渭河，质地多为中壤至重壤，通透性较好；黄绵土是由黄土母质经直接耕种而形成的一种幼年土壤，是黄土高原面积上最大的农业土壤，疏松软绵，通透性较好。其基本理化性质如表1所示。风干后过5 mm筛备用，其风干后备用的土壤初始含水量见表2。

表1 土壤基本物理性质Tab.1 Fundamental soil physical property

注：试验采用吸管法测定土壤颗粒组成，比重瓶法测量土密度，恒体积法测饱和导水系数。

表2 土壤初始含水量Tab.2 The initial soil moisture content

1.2 试验设计

膨胀性土壤吸水膨胀变形主要受膨胀力和自重应力影响，导致土壤入渗过程随着土壤深度的变化而变化。为了定量分析膨胀性土壤对土壤降雨入渗产流过程影响，试验设置4个厚度，分别为10、20、30、40 cm，每个处理两个重复，分别标记为：娄土10 cm、娄土20 cm、娄土30 cm和娄土40 cm。

试验时，将经5 mm筛的土壤分层(10 cm)均匀装入土槽中，土壤装填过程中严格控制了土壤容重，因此吸水变形前土壤剖面密度相同，因此密度变化只能发生在注水以后和降雨过程中吸水膨胀变形。土壤吸水膨胀变形首先导致土壤颗粒体积变化，进而导致孔隙度变化。土壤吸水变形后土层厚度均发生变化，对此我们采用土柱法针对性测定了土壤饱和水分运动参数试验。土槽中间位置深度0、10、25、40 cm处安装Trime水分传感器，用以测定土壤水分动态过程。土槽设置两个出水口，分别为壤中流和地表径流。土壤装填时，首先在土槽底部铺设反滤作用的石子，厚10 cm；再在石子的上面铺设纱布，然后将过5 mm筛后的土壤按定密度(1.4 g/cm3)装入土槽。

试验进行前，向土槽注入足够水量(土壤达到田间持水量以上，并产生大量壤中流)后静置，待其膨胀量达到相应土壤含水量最大膨胀量后进行降雨试验。

试验过程中，用降雨系统进行人工降雨，每次降雨历时控制在350 min左右。试验中Trime水分测定系统记录水分动态。同时，对地表径流量、壤中流流量进行收集、量测。径流观测时间间隔，根据产流速度而定，由于壤中流退水较慢，因此加长相应观测时间，假如试验过程中不产生壤中流，则放弃测定。试验设置1个雨强，30 mm/h，1个坡度，5°。

试验主要观测资料：径流(地表径流量、壤中径流量)、土壤剖面水分动态、产流历时、降雨强度等。

2 试验结果与讨论

为了分析土壤膨胀性对降雨入渗产流的影响，根据试验结果，对比分析黄绵土和娄土这两种典型膨胀性土壤的土壤容重、土壤累积入渗量和土壤径流强度变化规律。

2.1 土壤容重随深度变化关系

降雨入渗试验后可测定土壤的干密度，研究发现土壤不同剖面的土壤密度发生了变化(表3)。黄绵土和娄土在各种厚度的膨胀性土壤受到膨胀力和重力双重作用均导致表层0～10 cm土壤平均干密度相对减小，10 cm以下深度土壤干密度随深度增加而相对增加。原因在于膨胀性土壤饱和后的土壤容重在土体自身重力和土壤膨胀力的共同作用下发生了改变。

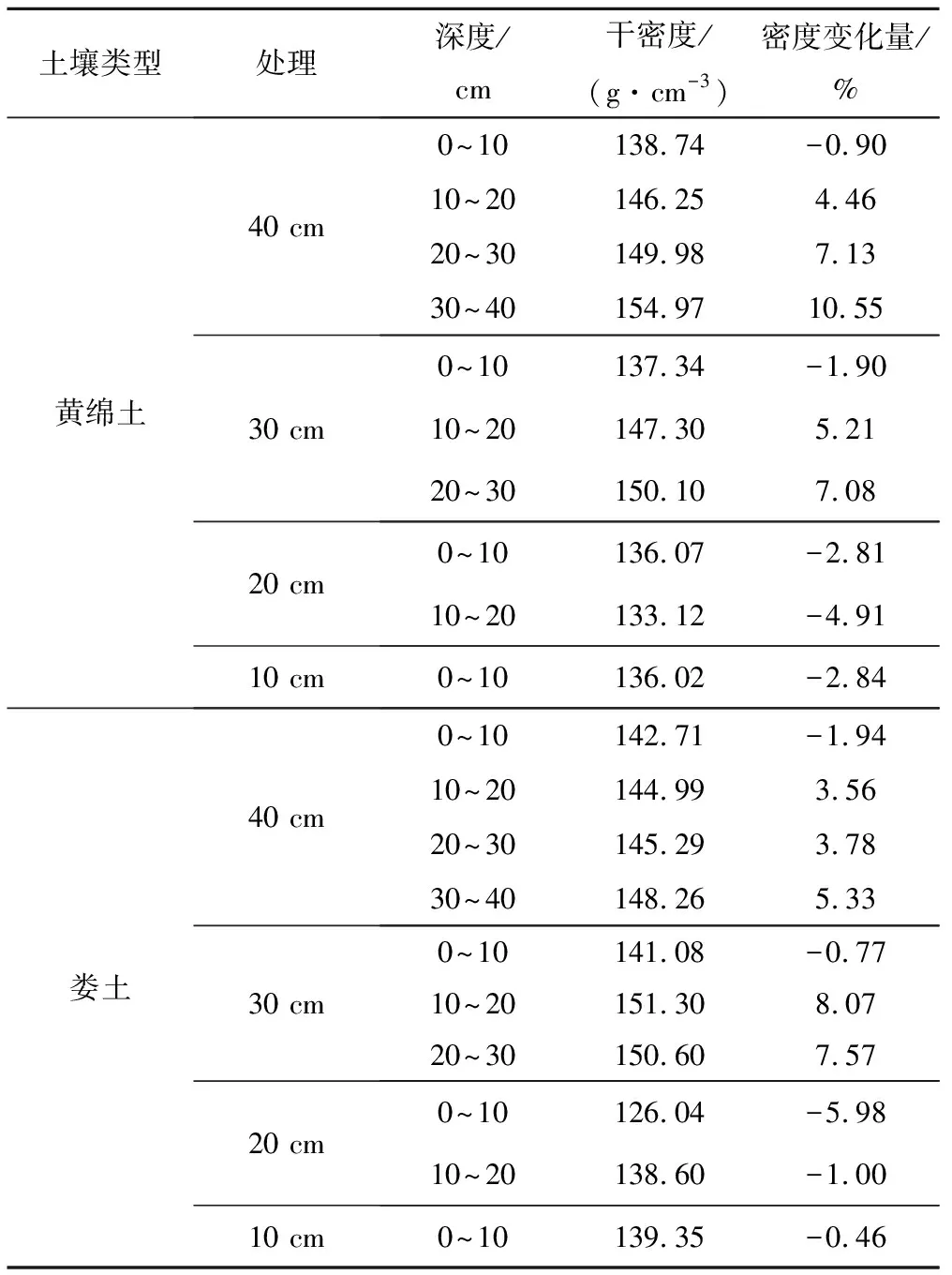
表3 土壤容重随深度变化统计表Tab.3 Changes of soil bulk density with depth

2.2 土壤累积入渗量随时间变化关系

黄绵土和娄土的土壤累积入渗量随时间变化关系如图1所示。土壤累计入渗量都随时间单调增大，且厚度越大累积入渗量越小。考虑是因土壤具有膨胀性，入渗过程中受到了土壤膨胀力和自重应力共同作用。深度较小时，主要受膨胀力导致孔隙度增加，导水率增加；随着土壤深度的增加，土壤自重应力占主导作用使土壤容重增大，孔隙度减小，土壤入渗率减小。相同条件下对比黄绵土，娄土的黏粒含量要高一些，导水系数较小，导致娄土的累积入渗量较小。

2.3 土壤径流强度随时间变化关系

径流强度随时间变化关系(图2)可以看出，不同土壤试验组中，初始入渗时间内径流强度变化很大，随入渗历时的逐渐增加，土壤径流强度也会逐渐增大，然后趋向稳定。而且对于不同土壤类型来说，如黄绵土的浅层土土壤颗粒较稳定，前期入渗的径流强度波动较小；娄土的深层土壤颗粒较稳定，在径流强度趋于稳定后波动幅度较小。当然，不同处理间相同时间时段内径流强度大小与降雨强度、入渗强度等也有密切关系。试验期间降雨系统具有一定不稳定性，有可能导致每次降雨强度出现一定偏差,进而导致地表径流强度规律出现一定混乱。

3 土壤特征水分运动曲线拟合

土壤降雨入渗产流过程中，对黄绵土和娄土不同厚度实验组采用Philip公式、Kostiakov公式和Horton公式进行土壤特征水分运动曲线拟合，对三种公式拟合结果精度加以分析。

3.1 Philip公式拟合结果

进行降雨入渗实验的过程中，土壤水入渗速率可以明显分为两个阶段：

(1)

式中：t1为土壤达到饱和所需时间，min；P为降雨强度，cm/min；S表示土壤吸湿率；A表示稳定入渗率。

Philip公式应用了MATLAB进行拟合，可以定量分析入渗过程中入渗时间和入渗率之间的关系(表4)。

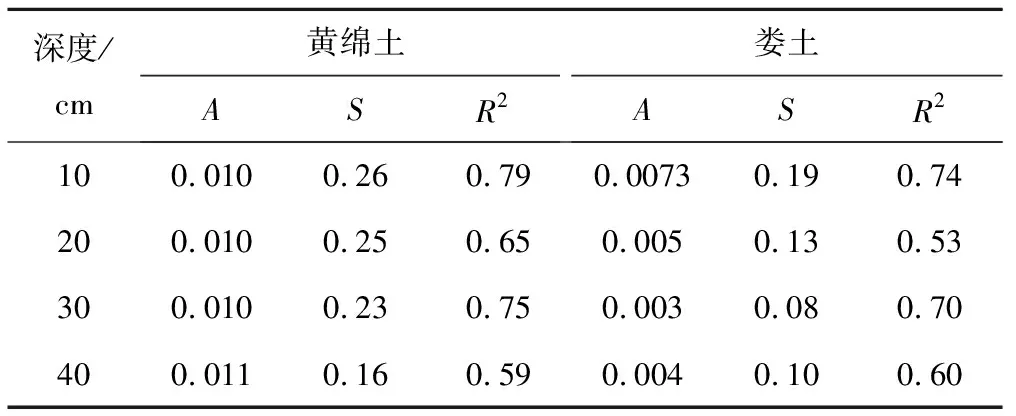
表4 Philip公式拟合结果Tab.4 Fitting result of Philip model

可以看出R2都在0.6左右，拟合效果一般，由实测数据拟合来看，Philip公式可以考虑应用在当忽略吸水时上层土体产生的压力水头或土壤吸水过程中所受重力。随着渗入时间的增大，膨胀土的入渗速率减慢，累积入渗量增加，而土壤吸水能力减弱。不同深度黄绵土的稳定入渗速率基本上不随深度变化而变化，娄土的稳定入渗速率会随深度的增加而减小，土壤入渗速率趋于平缓。拟合土壤入渗速率大都较高于实测土壤入渗速率，初步考虑是受膨胀性土壤入渗时体积变化，导致孔隙率增大，进而饱和含水量增大的影响，最后土壤吸力会减弱。

图1 土壤累计入渗量随时间变化关系Fig.1 Cumulative infiltration changed over time

图2 径流强度随时间变化关系Fig.2 The runoff intensity changed over time

3.2 Kostiakov公式拟合结果

在土壤水入渗过程中，Kostiakov公式可以看出土壤水累积入渗量随时间变化的趋势。入渗方程可以表示为：

(2)

式中：H为累积入渗量，cm；t为入渗时间，min；k为经验入渗系数，cm/min，表示入渗开始后第一个单位时段内的累积入渗量；α为土壤经验入渗指数，无量纲；f0为稳定入渗率，cm/min。

对上式求导，可得到入渗速率的表达式：

f=at-b+f0

(3)

式中：参数a可以用来描述入渗过程中时刻t时的入渗速率和稳定入渗速率的差值，参数a主要受稳定入渗速率f0的影响。

Kostiakov公式应用MATLAB拟合土壤水的入渗过程，拟合结果见表5。

表5 Kostiakov公式拟合结果Tab.5 Fitting result of Kostiakov model

由拟合结果看出，拟合过程中深度增加时，R2减小，但是Kostiakov公式整体拟合效果较好。饱和时的稳定入渗速率和初始入渗速率会对Kostiakov公式产生影响，而膨胀土吸水导致的体积变化对这两个值无大影响，所以Kostiakov公式的拟合情况较好。

3.3 Horton公式拟合结果分析

Horton公式考虑也分为两部分计算：

(4)

式中：P为降雨强度，cm/min；i0为t=0时的初始入渗率；ir为稳定入渗率；β为描述入渗过程中速率的减慢程度。

Horton公式的拟合结果见表6。在Horton公式拟合结果中，由参数β变化趋势看出，对于不同土壤来说，入渗速率都是随深度变化先减后增。而娄土的参数β值都比黄绵土的大一些，由此可以得出相同深度情况下娄土的入渗速率变化要快于黄绵土的。

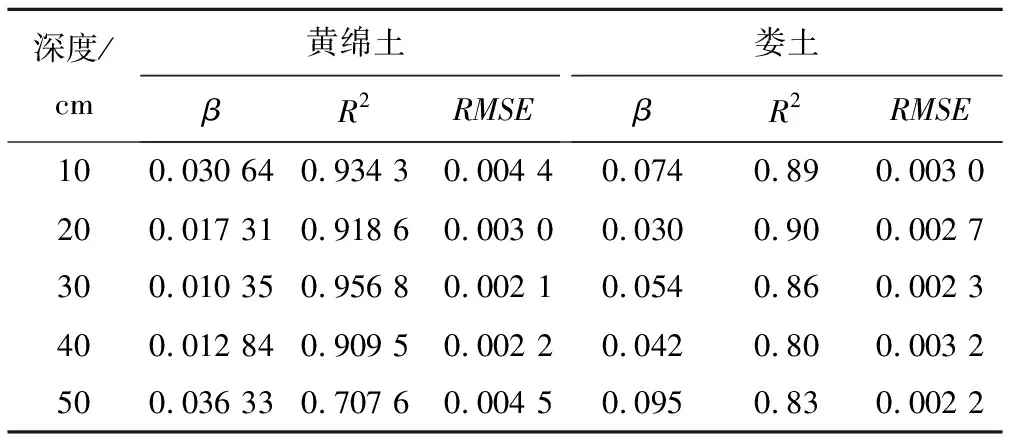
表6 Horton公式拟合结果Tab.6 Fitting result of Horton model

对于Horton公式的拟合，R2整体随深度变化呈减小趋势，即对浅层变形较小的土壤拟合效果较好，对深层变形较大的土壤拟合效果则较差。黄绵土的膨胀孔隙率小于娄土的，体积变化率也较小，其R2也较高，则考虑土壤类型和土壤体积变化对Horton公式拟合有一定的影响。

3.4 拟合结果讨论

对比Philip公式、Kostiakov公式和Horton公式拟合情况(图3、图4)，根据拟合结果，可以得出以下结论：①Philip公式只考虑土壤水的入渗速率仅与时间有关，拟合效果较差。而Kostiakov公式的拟合值与实测值最为相近，适合应用于降雨入渗模型。②Kostiakov公式和Horton公式的拟合效果都很接近于1。但是入渗速率存在差异，其中Kostiakov公式只考虑稳定入渗率随时间的变化关系，而Horton公式还把在土壤饱和过程中土壤水入渗速率的变化程度纳入考虑范围。由此可以看出Kostiakov公式更适合应用于土壤饱和段的拟合，Horton公式适用于初始入渗至稳定入渗的过程，是考虑膨胀土体积变化的土壤水分特征曲线拟合的模型。

本文主要对黄绵土和娄土两种土壤类型不同厚度试验组进行试验，而采用拟合的3种模型模拟结果显示黄绵土的相关系数R2大部分高于娄土的，其主要因由是在入渗过程中黄绵土吸水膨胀率要小于娄土的，受到了土壤的水分特征参数影响(不考虑误差)。

4 结 语

本文是在积水入渗试验的基础上，对黄绵土和娄土这两种典型膨胀性土壤进行室内降水入渗试验，试验计量出膨胀性土壤在降雨入渗产流下的各参数动态变化。可得出以下结论：①在土壤降雨入渗过程中，膨胀性土壤会吸水膨胀变形，使土壤受到其自身重力还有膨胀力的共同作用，导致土壤容重发生改变。②相同入渗时间内，土壤厚度越大，土壤累计入渗量会越小，但是大小幅度会受到土壤类型不同、土壤入渗位置和降雨强度等影响。③降雨入渗试验过程中，Horton公式适用于初始入渗至稳定入渗的过程，Kostiakov公式适合应用于降雨入渗模型土壤饱和段的拟合，而 Philip公式并不适合降雨条件下膨胀性土壤水分入渗特征曲线拟合。

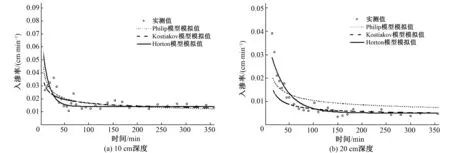
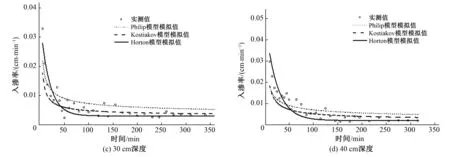
图3 娄土土壤水分特征曲线拟合结果图Fig.3 Schematic of the fitting result of each model for Lou soil

图4 黄绵土土壤水分特征曲线拟合结果图Fig.4 Schematic of the fitting result of each model for loessal soil

□