强剩磁条件下磁性目标三维正则化聚焦反演方法

李金朋， 张英堂， 范红波， 李志宁， 张光

(1.陆军工程大学石家庄校区 车辆与电气工程系， 河北 石家庄 050003； 2.65185部队， 辽宁 铁岭 112611)

0 引言

磁法勘探主要应用于军事侦察(未爆弹、潜艇和水雷等)、水文及工程地质勘探等领域[1-2]。反演是解释磁性目标的重要一步，其主要目的是利用获得的磁性目标磁测数据来评估地下或水下未知磁性体的轮廓形态[3-4]。在反演过程中，常常假设磁性体仅包含感应磁化而忽略剩余磁化影响。然而，在实际测量中，磁性体除了会受到感应磁化，还会受到剩余磁化的影响，导致总磁化方向产生改变，进而影响磁测数据的解释精度[5-6]。

针对强剩磁条件下的反演方法，国内外学者进行了一系列相关研究。第一种方法是首先估计磁化方向，然后利用磁化方向估计值对磁性体进行反演[7-8]。该方法的缺点是仅适用于孤立磁源，对于多目标磁源则无法利用此方法进行反演。第二种方法是将获得的磁异常值转化为受剩余磁化影响小、与场源位置对应良好的转换量，然后利用转换量进行后续反演[9-11]。上述基于转换量的反演方法不仅适用于孤立场源，也适用于磁化方向不同的多个场源体，缺点是由于缺乏相位信息，仅能反演出场源体的大致位置。同时，在反演过程中，由于实际测量数据中存在噪声和固有的场源不唯一性，导致磁性目标的反演是病态多解的。为了减少测量误差等因素的影响，常常使用L2或Tikhonov正则化思想[12-13]。吴小平等[14]提出将共轭梯度法应用于电阻率三维反演；朱自强等[15]利用混合正则化反演方法减弱了反演的聚焦效应，能有效获得异常边界；杨娇娇等[16]通过向目标函数中引入深度加权函数来提高对目标深度信息的识别能力；秦朋波等[17]利用再加权的方法实现深度加权，对目标进行反演；Wang等[18]利用改进的预处理共轭梯度法对航空重力数据进行反演，提高了反演速度和效果。上述方法为磁测数据反演提供了较好的思路，但是在反演过程中正则化参数的选择常采用经验定值，导致计算精度较低，难以达到最佳的拟合效果。

本文针对上述反演过程中存在的问题，提出了强剩磁条件下磁性目标三维正则化聚焦反演方法。通过向目标函数中引入深度加权矩阵和最小支撑矩阵，避免了反演解的不稳定性；对目标函数进行奇异值分解(SVD)，并利用无偏风险估计(UPRE)准则对正则化参数进行自适应选择，实现了迭代过程的自动化。根据磁总场模量数据对磁源数量进行判断，在反演数据的选择上，针对孤立磁源，利用磁化方向估计方法获得实际磁化方向，通过磁梯度张量数据进行反演；针对多目标磁源，采用磁总场模量数据进行反演。

1 三维正则化聚焦反演理论

1.1 Tikhonov正则化反演理论

磁性目标正演公式为

do=Am+e，

(1)

式中：核函数矩阵A的元素Aij为第i(i=1，2，3，…，p)个观测点观测的第j(j=1，2，3，…，n)个单元的响应；do∈Rp为观测数据矩阵；m∈Rn为待测模型参数矩阵；e∈Rp表示实测数据中的误差。

根据(1)式可知，磁性目标的反演过程就是利用包含噪声的实测数据do求解模型参数m. 利用Tikhonov正则化公式，可将目标函数矩阵转化为如下最小二乘公式：

(2)

(3)

(4)

(5)

因为矩阵D为可逆矩阵，所以

(6)

(7)

m(α)=ma+D-1J(α).

(8)

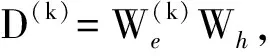
(9)

m(k+1)=m(k)+(D(k+1))-1J(α(k+1)).

(10)

(11)

式中：ui和vi分别为矩阵U和V的第i列。

1.2 UPRE正则化参数选择方法

(12)

(13)

残差的二范数均值

(14)

因此最优正则化参数αo表示为

(15)

在Tikhonov正则化方法中，常常利用经验定值或L-curve曲线等方法对正则化参数进行定值选择[12-13]，在迭代过程中正则化参数不随迭代过程而发生改变。而本文提出的UPRE准则在迭代过程中不断地优化和求解迭代参数，实现了正则化参数的自适应选择。

2 强剩磁条件下反演理论

磁梯度张量数据在反演过程中具有高的模型分辨率。但是，在强剩磁条件下模型的实际磁化方向难以判别，进而影响最终的反演结果。针对孤立磁源，可以通过计算其实际的磁化方向进行反演。当待测模型体为多目标磁源时，在剩磁影响下，直接利用磁梯度张量进行计算的精度将大大降低，因此，需要采用弱敏感于磁化方向的磁总场模量数据来进行反演。

2.1 孤立磁源

针对孤立磁源，本文提出了利用归一化磁源强度和化极(NSSRP)互相关的方法对磁化方向进行估计。

归一化磁源强度是由磁梯度张量矩阵推导出来的1个旋转不变量，其分布位于场源中心。基于这种性质，在磁化方向未知情况下将铁磁形体的磁倾角和磁偏角等间隔地选取一系列数据点，组成磁化方向暂定值。利用这一系列磁化方向下的化极异常值与归一化磁源强度进行试错，可得到不同的互相关系数，其中互相关系数最大值对应的磁化方向即为磁化方向估计值。

定义实测区域内的磁异常化极结果ΔTr与归一化磁源强度数值Tn的互相关系数C为

(16)

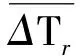
2.2 多目标磁源

针对多目标磁源，本文利用磁总场模量进行反演。磁总场模量数据为弱敏感于磁化方向的转换量，其定义为

(17)

式中：Ba为总场磁异常矢量，|Ba|为磁异常矢量的模量；Bx、By和Bz分别为磁场矢量在x轴、y轴、z轴方向的分量。

由(17)式可以看出，磁异常模量与地下待测模型间呈非线性关系，因此需要计算其核函数矩阵。在模型进行第k次迭代时，Ba的第v个分量Bav对地下第w个模型参数mw的核函数矩阵Avw为

(18)

在实际应用中，由于磁总场模量数据受剩余磁化方向的影响较小[7]，其主正极值与实际磁性体分布位置基本一致，根据磁性体的磁总场模量异常数据可以判断出磁性体的实际分布数量。

3 数值仿真

为了便于对不同磁测数据的反演效果进行分析，构建一个正演模型对上述方法进行验证。将地下待测空间划分为22×22×10=4 840个单元格，每个单元格均为边长为0.1 m的正方体，地下正演模型如图1所示。正演模型的感应磁化方向I=60°，磁偏角D=-20°，总磁化方向I=50°，磁偏角D=135°.

3.1 磁梯度张量反演

在强剩磁条件下利用磁梯度张量数据进行反演，需要已知磁性体的实际磁化方向。如图2所示，在反演过程中向磁梯度张量分量Azz中加入0.05×std(d,1)×rand(484,1)的误差作为实测数据，其中d表示待测数据的理论值。分别利用本文提出的NSSRP互相关系数法及Gerovska[6]提出的利用磁总场异常和化极(TMFRP)的互相关估计方法对磁化方向进行估计，得到的总磁化方向估计值如表1所示。

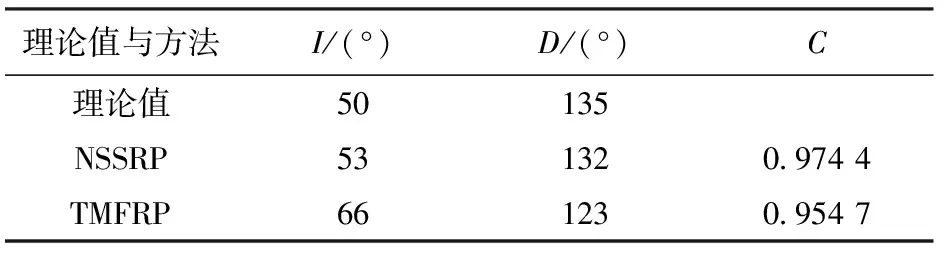
表1 两种方法磁化方向估计结果

从表1中可以看出，与TMFRP互相关法相比，NSSRP互相关法具有更高的求解精度，进一步证明了本文磁化方向估计方法的有效性。利用磁化方向估计值对Azz分量进行反演，获得的反演结果如图3所示，其中白色实线为异常体的实际轮廓位置。根据反演结果可知，其倾斜轮廓是清晰可见的，其水平和垂直分辨率较高，能够较好地反映磁性体的实际轮廓。仿真结果表明：利用NSSRP互相关系数法能够提高磁化方向的估计精度，利用磁梯度张量分量Azz进行反演，获得的结果具有较好的横向和纵向分辨率。

3.2 磁总场模量反演

针对图1所示的正演模型，根据(17)式计算正演所需要的模量数据，并利用磁总场模量数据进行反演。分别计算感应磁化条件下和总磁化条件下的磁总场模量数据，获得磁总场模量数据如图4所示。从图4中可以看出，在两种磁化方向下获得的模量数据具有高度一致性，证明了模量数据对磁化方向的不敏感性。利用模量数据进行反演，获得的反演结果如图5所示。与磁梯度张量Azz单分量反演方法相比，其横向和纵向的模型轮廓分布较好，但是其倾斜度并不明显。这是因为模量数据仅包含幅值信息，并不包含相位信息。

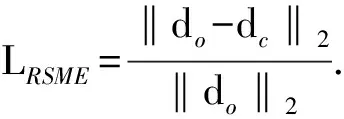
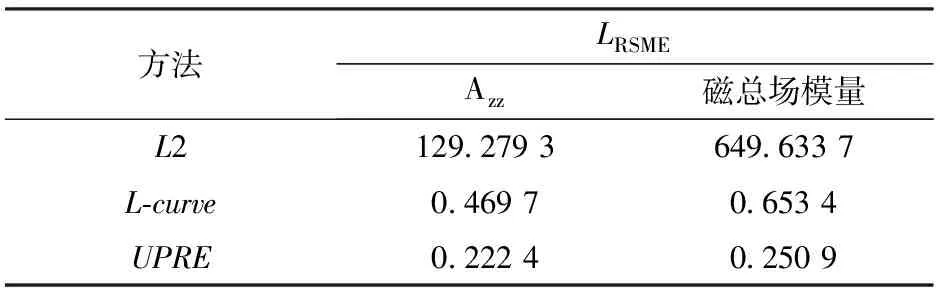
表2 平均相对误差LRSME

通过对两种磁测数据的反演结果进行分析可知：利用磁梯度张量分量Azz进行反演获得的结果具有较好的横向和纵向分辨率，但是在实际应用过程中，该方法仅能对孤立磁性目标进行反演；利用磁总场模量数据进行反演，能够有效规避需要已知磁化方向这一条件，在实际反演过程中更加灵活，能够实现对组合磁性目标进行反演，但是反演效果较Azz分量稍差。因此，在反演计算过程中，需要根据实际情况选择合适的磁测数据进行反演计算。

4 实验验证

为了验证上述方法的有效性，下面进行两组实验。测区位于石家庄市某地，其背景磁化方向I=55°，磁偏角D=-16°，实测区域如图6所示。实验所用探头是利用英国Bartington公司三轴磁通门传感器搭建的十字型磁梯度张量探头，测试系统主要包括十字型探头和数字采集模块及软件操作终端。实验过程中探头固定在无磁实验台架上，利用扫描方式对待测区域的每一个观测点进行测量。

4.1 孤立磁源

第1组实验是对一块长方体铁板进行测试。在地理坐标系下，铁板中心坐标为(1.25 m,0.85 m,0.45 m)，尺寸为0.7 m×0.5 m×0.1 m. 获得的实测Azz数据如图7所示。利用NSSRP互相关估计法对其磁化方向进行估计，获得的估计结果如表3所示。从表3中可以看出，获得的磁化方向估计值与背景磁场存在较大差异，证明了磁性体具有强剩磁存在。利用NSSRP互相关法得到的磁化方向估计值作为总磁化方向，分别利用Azz分量和磁总场模量进行反演，获得的三维反演结果为磁化强度大于0.3×maxm(α)所显示的结果，如图8和图9所示。根据获得的反演结果可以看出，利用Azz数据进行反演能够获得更好的横向和纵向分布结果，其中在Azz反演过程中存在两块磁性体的原因是反演过程中受测量误差和环境因素等干扰所导致的。根据表4中LRSME的计算结果也可以看出，利用Azz反演获得的计算结果具有更高精度。

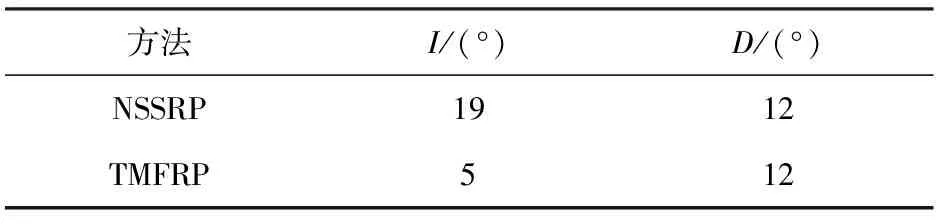
表3 磁化方向估计结果

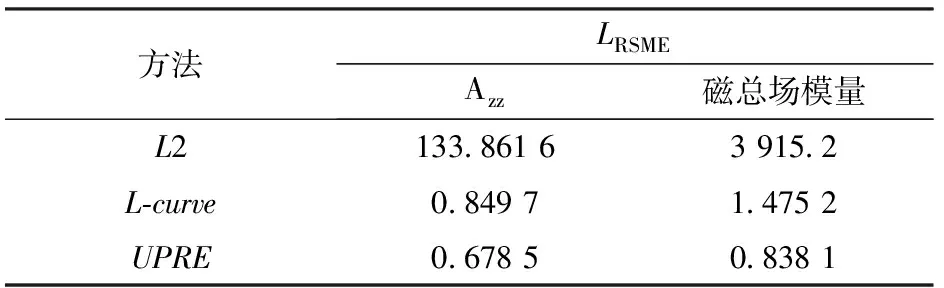
方法LRSMEAzz磁总场模量L2133.861 63 915.2L-curve0.849 71.475 2UPRE0.678 50.838 1

4.2 多目标磁源

第2组实验对水平圆柱体铁筒和长方体铁块的组合磁异常进行测试。长方体铁块位于测区东南方向，中心坐标为(1.5 m，0.4 m，0.3 m)，尺寸为0.23 m×0.36 m×0.20 m，铁筒位于测区西北方向，中心坐标为(0.6 m，1.2 m，0.2 m)，圆筒直径为0.1 m，长为0.46 m. 获得的实测数据如图10所示。针对组合铁磁性体，分别利用Azz分量和磁总场模量反演方法进行反演，获得的三维反演结果如图11和图12所示。

根据获得的反演结果可以看出，利用Azz数据进行反演时，利用背景磁场的磁化方向进行反演，获得的反演结果与磁性体的实际位置偏差较大，在剩余磁化影响下，对磁性体的实际反演结果产生了较大的影响。利用磁总场模量数据进行反演时，能够获得更好的横向和纵向分布结果，根据表5中LRSME的计算结果也可以看出，该方法获得的计算结果具有更高精度。单次迭代时，利用Azz进行反演的时间为0.106 s，利用磁总场模量异常进行反演的时间为0.342 s，这是因为在计算过程中后者需要3个灵敏度矩阵，其计算成本约为前者方法的3倍。

5 结论

本文提出了强剩磁条件下磁性目标三维正则化聚焦反演方法，向目标函数中引入深度加权矩阵和最小支撑矩阵并利用SVD法对目标函数进行分解，通过UPRE对正则化参数进行自适应选择。在反演数据的选择上，针对孤立磁源，通过磁梯度张量数据进行反演；针对多目标磁源，采用磁总场模量数据进行反演。得到如下主要结论：

1)利用深度加权矩阵和最小支撑矩阵对经典Tikhonov正则化理论框架下的反演模型进行约束，提高了反演解的稳定性。

表5 平均相对误差LRSME

2)采用UPRE对迭代过程中的正则化参数进行选择，实现了正则化参数选择的自适应功能。

3)提出了适用于多种磁源情况下的磁性目标反演方法，能够同时对多种磁性体进行反演，并获得较高的反演精度。