基于航班延误的机位冲突概率计算方法

丁 聪，毕 军，张 俊

（1.北京交通大学城市交通复杂系统理论与技术教育部重点实验室，北京 100044；2.云南航信空港网络有限公司，云南 昆明 650051）

0 引言

机位分配是指机场根据航班计划表和停机位的利用状况，为每个进出港航班分配合适的停机位，是机场运营过程中的一个关键环节。然而恶劣天气、机场流量控制以及地面保障工作等随机因素会造成航班时刻扰动，若计划分配至同机位的航班因延误导致机位占用时间冲突，分配方案必须进行实时动态调整。对于大型机场而言，有限的机位资源和高密度的航班起降使得停机位调度工作强度大、作业成本高，且依赖工作人员的经验，影响机场的运行效率。

既有研究中，吸收延误的一般方法是通过增加某些约束条件或设置优化目标来控制航班的延误传播。国际上，Yan等[1]通过在分配至同一机位的连续航班之间设置一个固定的空闲时间来吸收航班的不确定延误；Bolat等[2-4]以机位空闲时间均衡作为目标函数建立机位分配模型。国内，王岩华等[5]、高菁等[6]所建机位分配模型中也设置最小时间间隔为安全约束。然而这些方法实质上只是为机位设置了定性的缓冲时间，针对性不强，并不能完全反映两个航班可能实际面临的机位冲突情况。Lim等[7]虽然对机位冲突概率进行了量化研究，但缺点在于模型对机位冲突的处理采用假设方式，没有基于实际运行数据进行深入分析。

本文将基于昆明长水国际机场的实际航班数据，分析各航班延误的规律，定量研究其对于冲突发生概率的影响。然后通过设置合理的间隔时间来吸收延误，减少后期频繁变更，以便保证机场的高效运作。

1 航班延误时长的分布规律与检验

本文数据来源于昆明长水国际机场2016年4月1日—2016年12月31日3个季度的实际生产运行数据，航班记录14万条左右。该机场日均航班量可达1 000架次以上，已基本呈现饱和状态。

首先，利用航班的预计抵达时间、实际抵达时间、预计起飞时间、实际起飞时间计算出航班的到达与起飞延误。然后，分别对机场航班到达延误与起飞延误时长进行统计，并绘制直方图，发现航班到达延误与起飞延误的分布存在显著差异。进港航班到达延误的直方图呈正态分布，中部高，两端低，且提前到达与延误到达的航班数量大致相同；而离港航班起飞延误直方图则呈明显的右偏规律和厚尾现象，延迟起飞的航班数量远大于提前起飞的航班数量。这主要是由于离港航班的起飞时间依赖前行进港航班，进港航班延迟到达目的机场并造成相应离港航班起飞延误的可能性增加。鉴于到达延误与起飞延误时长明显的分布差异，可以假定航班的到达延误符合正态分布规律，而起飞延误符合混合正态分布规律。

1.1 航班到达延误规律检验

若航班的到达延误时长符合正态分布规律，则其概率密度函数为：

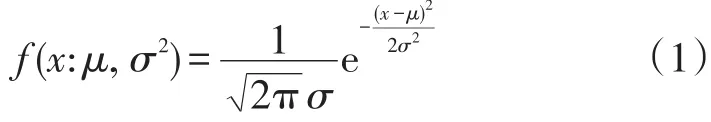
式（1）中：x为到达延误时长（min）；f(x)为到达延误x的概率；μ和σ分别为航班到达延误时长的均值（min）和标准差。

在检验样本数据分布是否符合正态分布规律的众多方法中，选取JB（Jarque-Bera）检验进行验证。它是利用正态分布的偏度和峰度，构造出一个统计量JB，即：

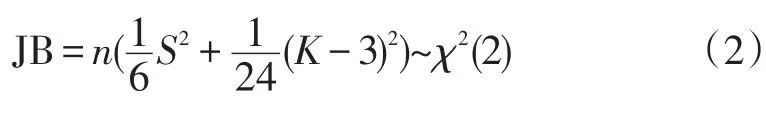
式（2）中：n为样本容量；S为样本的偏度；K为样本的峰度。

假设显著性水平为α，则当JB统计量小于自由度为2的卡方分布的1-α分位数时，接受原假设，认为样本符合正态分布规律；否则拒绝原假设。该方法应用于大样本数据时效果较好。如果样本符合正态分布，则偏度为0，峰度为3，JB统计量为0。

因此，有关航班到达延误时长分布规律的研究分为以下三步：

（1）对航班延误样本数据进行JB检验，结果正确，令H=0，转下一步。

（2）使用极大似然估计法，基于航班延误样本数据对航班到达延误的总体分布进行参数估计，计算出到达延误分布概率密度函数中各参数的取值。

（3）采用χ2拟合优度检验法进行假设检验。当H0=0时，假设成立；当H0=1时，拒绝原假设。显著性水平α=0.05。

1.2 航班起飞延误规律检验

假定航班起飞延误时长服从混合正态分布：

式（3）中：ρ为0～1之间的实数；ϕi(x)(i=1,2)为以μi为均值，以σi2为方差的正态分布概率密度函数。该式表示x以ρ的概率服从以ϕ1(x)为密度函数的正态分布，以1-ρ的概率服从以ϕ2(x)为密度函数的正态分布。

估计混合正态分布中各参数的方法如下。

设X1,X2,…,Xn为来自同一分布的随机样本，x1,x2…,xn为对应的观测值，则其似然函数为：

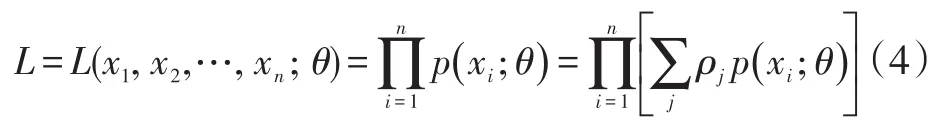
式（4）中：p(xi;θ)为单个正态分布的概率密度函数。

或

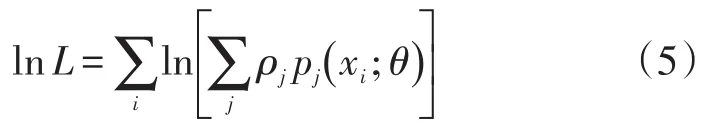
为求式（5）的极大值，采取一种快捷且易于计算的期望最大化（Expectation Maximization，EM）算法通过迭代循环进行逼近，每一次迭代由两步组成：E步（求期望）和M步（极大化）。

E步：在给定t轮参数的条件下，计算每个xi属于第j正态分布的条件概率：

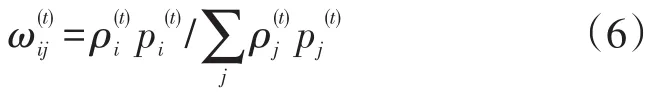
M步：根据和xi，给出θt+1的极大似然估计：

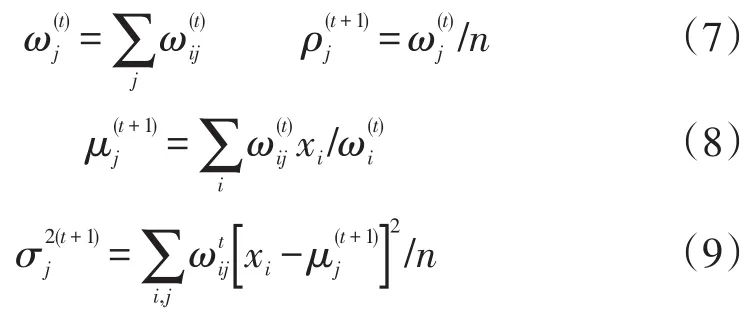
在上述两步反复迭代的过程中，lnL将逐渐收敛，直到达到设定的收敛标准时，计算停止，此时所得有关参数θ即为极大似然估计。

由于一般正态分布的检验方法并不适用于检验混合正态分布，本文采用交叉验证法对其进行检验：

2 同机位航班冲突概率计算方法

现计算分配至同一机位的前后两航班的冲突概率。如图1所示，在机位分配计划中，航班1和航班2为分配至同一机位的航班，假定航班1先进入机位，计划于ETA1时刻抵达，进行上下客和其他检查后于ETD1时刻起飞，若用td1表示起飞延误，则对应的概率密度函数为。机位空闲一段时间后航班2准备进入相同机位，计划于ETA2时刻抵达，若用表示到达延误，则对应的概率密度函数为。若航班1延误后实际起飞时间大于航班2提前抵达后（也可能延误）实际到达时间，即时，则认为航班1与航班2发生冲突。

航班1和航班2发生冲突的概率Pconflict为：

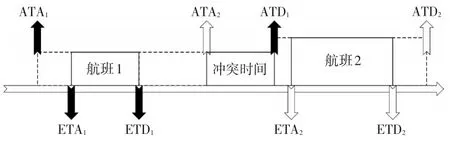
图1 同机位连续航班冲突示意图

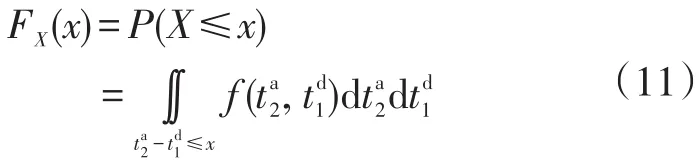
又由于航班1和航班2相互独立，因此航班1的起飞延误和航班2的到达延误事件也相互独立，则式（11）又可表述为：

以前文所得航班到达延误和起飞延误分布模型为例，有：

将式（13）及式（14）带入式（12）得：

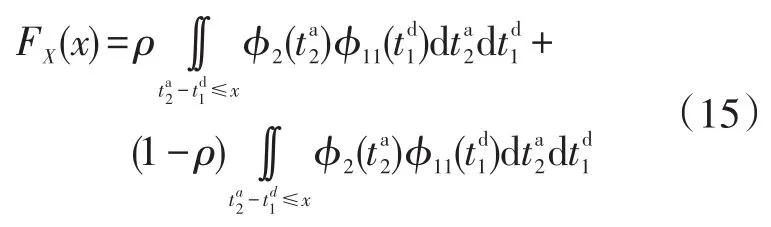
根据定理：对于n个独立正态随机变量，若，且各变量间相互独立，则差Z=X1-X2-…-Xn仍然服从正态分布，且有

对式（15）两边求导得：

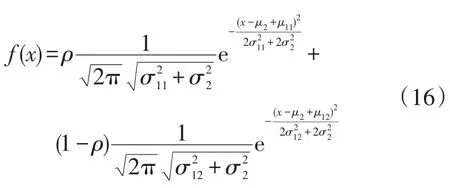
因此：

由式（17）可得，指派至同一机位的两连续航班间发生时间冲突的概率不仅与两航班间的机位空闲时间有关，还取决于这两个航班的延误分布。前后两航班发生机位冲突的概率可用下式计算：

式（18）中：ETD1-ETA2为两航班间的空闲时间（min）；分别为起飞延误的混合分布中两正态分布的均值与方差；分别为抵达延误分布的均值与方差。

3 实例分析

利用Matlab平台对航班到达延误与起飞延误分布进行检验与参数估计。以某航班为例，首先对航班到达延误的样本数据作JB检验，得H=0。因此判定航班到达延误总体服从正态分布，并采用极大似然估计法进行参数估计，得到其概率密度函数为：

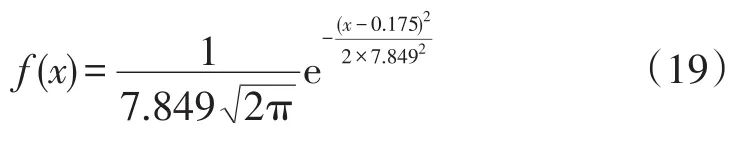
式（19）中：x为航班到达延误时长（min）；f(x)为概率密度函数；

采用χ2拟合优度检验法对以上结论进行检验，得到H0=0，证明航班到达延误时长服从正态分布。拟合结果如图2所示，其中航班到达延误若为负，表示相对于计划到港时间提前到达；若为正，则表示相对于计划到港时间延迟到达。

根据1.2节的方法对起飞延误时长的混合正态分布进行检验和估计，得到其概率密度分布函数为：

图2 航班到达延误时长分布图

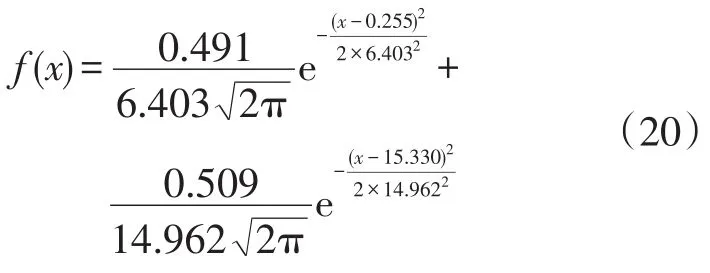
式（20）中：x为航班的到达延误时长（min）；f(x)为概率密度函数。

本文取P=90%，以及两种情况来检验模型的泛化能力，结果如表1所示。

表1 航班起飞延误时长概率密度模型泛化能力检验结果

二阶混合正态分布的拟合结果如图3所示。

图3 航班起飞延误时长分布图

根据上述拟合所得航班到达延误和起飞延误分布规律，设置空闲时间间隔从0min增加至50min，带入式（18）进行计算，得到冲突概率随空闲时间间隔的变化趋势（如图4所示）。冲突概率和空闲时间间隔的对应关系如表2所示。

图4 同机位连续航班空闲时间与机位冲突概率关系曲线

表2 同机位连续航班空闲时间与机位冲突概率关系表

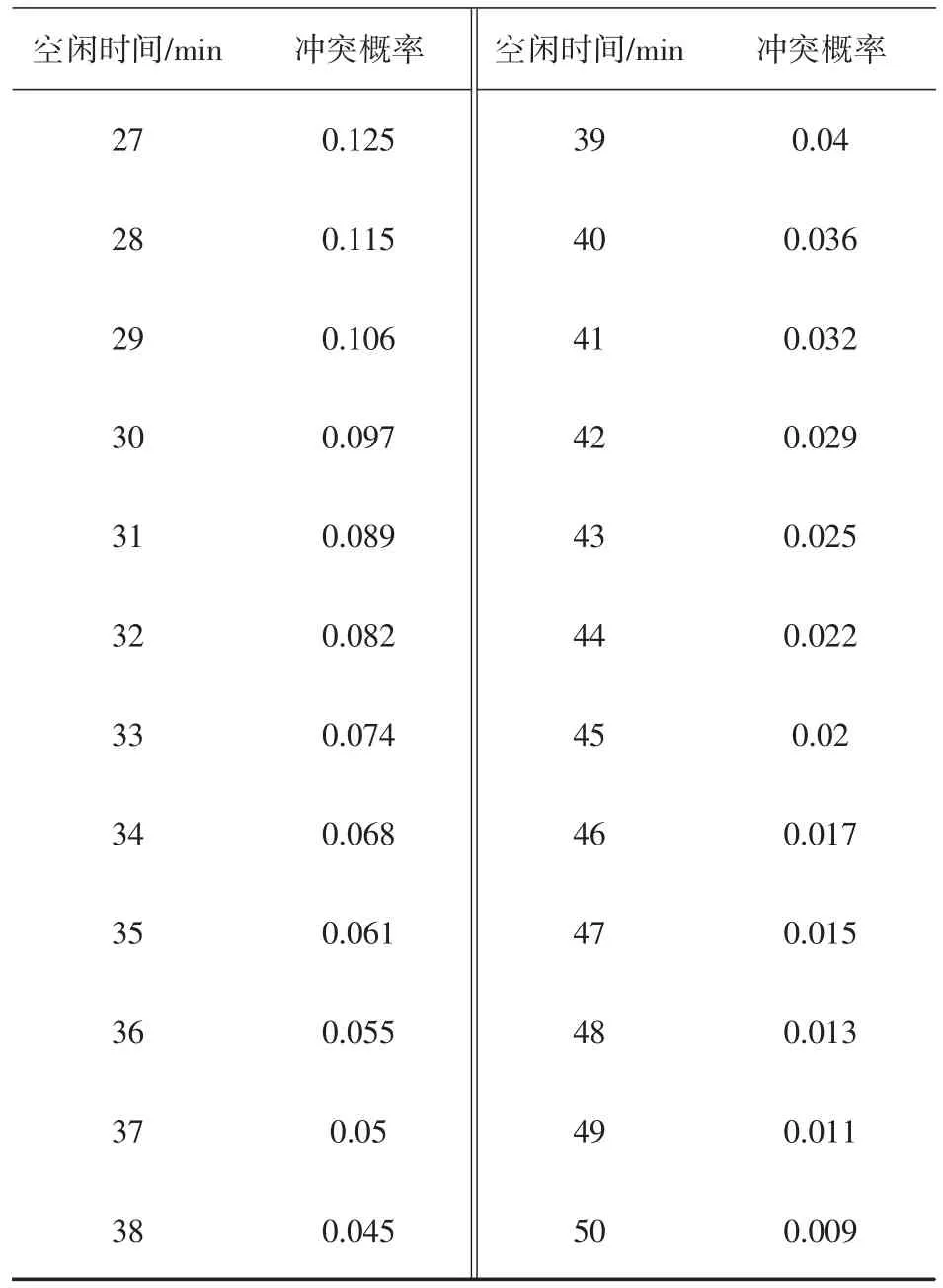
表2（续）

从表2可以看出，同机位连续航班的空闲时间间隔从1min增至15min时，冲突概率下降了0.343，变化较为显著；从15min增至30min时，冲突概率仅下降了0.194，变化幅度变小；随着空闲时间的继续增加，同机位冲突概率变化的显著程度进一步降低。

4 结论

通过对大量实际航班数据的分析和验证，本文得出航班的到达延误符合正态分布，起飞延误符合混合正态分布的规律；推导出的同机位连续航班间冲突概率的计算公式能够定量描述产生冲突的概率随间隔时间的增大而降低的关系。不同的航班其延误规律不同，在制订分配方案时可利用航班间的冲突概率大小来定量决定是否将两者安排至同机位或者为容易扩散延误的敏感航班合理分配航班时隙。但是，间隔时间过长会影响机位使用效率，所以机位使用效率与冲突概率之间的多目标优化问题还有待进一步研究。