基于PSO算法的某型飞机起飞阶段参数辨识及性能分析

， ， ，

(1.空军工程大学 航空工程学院，西安 710038; 2.中国人民解放军63870部队，陕西 华阴 741200)

0 引言

面对未来复杂多层次化的现代战争，对军队和武器装备提出了更高要求，空中部队作为先头打击部队首当其冲，军事斗争训练准备水平直接决定部队战斗力。飞机性能分析作为飞行训练评估的一个重要方面，引起了学者的广泛关注，研究表明起飞着陆阶段发生事故的比例约占飞行事故的65%左右[1]。因此，对起飞着陆阶段的研究和性能分析具有极其重大的军事意义。

飞机起飞阶段最重要的性能就是起飞距离，但在实际计算中我们缺少相关的气动参数，以往飞行器气动参数的确定是通过理论计算和风洞试验进行的，而理论计算有其局限性，风洞试验与实际飞行条件也存在差异，两者所得到的气动特性均难以准确反应实际飞行特性。因此要对起飞进行性能分析首先要解决飞机的气动参数辨识；近年以来，众多学者在飞行器动力学系统辨识领域开展了大量的研究[2-10]，针对具体的研究对象建立了各种数学模型，提出了各种类型的辨识算法，而针对飞机起飞阶段动力学参数辨识研究则相对较少。于雪梅[11]等研究了利用极大似然法对飞机起飞性能参数进行辨识，但是该方法对于待辨识参数的初值要求较高，在计算灵敏度时也会带来一些数值方面的问题，从而在一定程度上影响了参数辨识结果的准确性。类似于极大似然法的等传统优化算法进行求解会涉及到函数的梯度计算以及迭代初值的选取等一系列问题影响辨识结果，而目前快速发展的智能算法由于其强大的全局搜索能力和不受初值影响的特点，已被广泛应用于参数辨识中[12-17]。钱炜祺[15]等人应用遗传算法对某型飞机纵向气动参数进行了辨识，结果表明算法不受参数初值选取的影响,具有较好的全局寻优特性。粒子群和遗传算法相似，但比遗传算法规则更为简单、操作简单、有更强的鲁棒性和全局寻优能力。张天姣[14]等人应用粒子群算法针对战术导弹的纵向和横向气动力参数进行了辨识研究，结果证实该算法在气动力参数辨识的有效性，不受辨识参数初值选取的影响，具有较好的全局寻优性能和较强的鲁棒性。

鉴于上述分析，在日常飞行训练飞行数据的基础上，本文采用PSO寻优算法对某型战机起飞阶段的模型参数进行辨识，依据真实的飞行数据对飞机起飞阶段飞行性能进行分析，分析了气压高度、起飞质量和温度三个因素对某型飞机滑跑距离和滑跑时间的影响。所得结论可以为部队飞行训练评估提供参考 。

1 起飞阶段性能建模

1.1 起飞过程

起飞前，飞机滑跑到起飞线上，踩住刹车，飞行员推油门杆使得发动机达到最大转速，松开刹车飞机开始加速滑跑，当滑跑速度达到一定数值VR(抬前轮速度)时，飞行员向后拉驾驶杆使得飞机抬头前轮离地。飞机抬头后，飞机的迎角不断增大，飞机的升力随滑跑速度和迎角的增加而增大，当速度达到Vlof(离地速度)时，飞机的升力L等于飞机自身重量W时飞机自然离地。飞机便开始离开地面以后，飞机加速上升爬升，飞行员控制飞机爬升的姿态角，直到当飞机爬升到安全高度，飞行员便开始收起落架以减小飞行阻力，起飞过程完成。从飞机的起飞过程可以看出，飞机的起飞大致可以分为地面加速滑跑和空中加速起飞上升两个阶段，而在地面滑跑时，又分为三点滑跑和两点滑跑。图1为飞机起飞过程示意图。

图1 飞机起飞过程

1.2 起飞滑跑阶段模型建立

飞机的滑跑距离和起飞时间是飞机起飞性能的两个重要指标，直接影响机场跑道的长度和飞机的出动效率。起飞距离过长，会对机场跑道提出更多要求，起飞时间过长，容易贻误战机，失去制空主动权；因此对飞机起飞性能的分析与评价可以为军事斗争训练评估提供决策参考。

飞机在滑跑时，受到发动机推力T、垂直于飞机运动方向的升力L、地面支持力N、与飞机运动方向相反的空气阻力D和跑道摩擦阻力F的共同作用。水平和垂直方向受力示意图如图2所示。

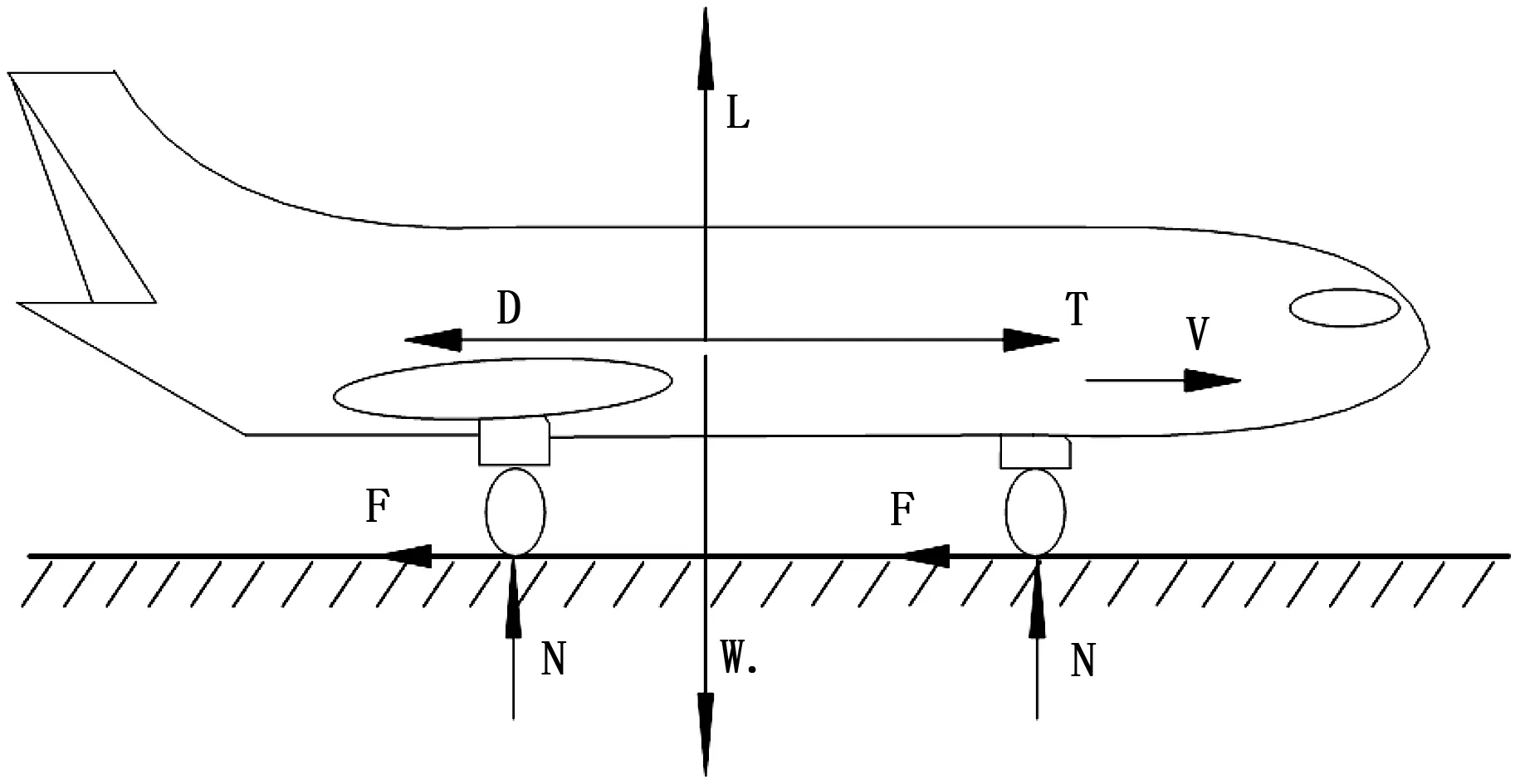
图2 起飞滑跑时飞机受力情况

滑跑阶段假设飞机平行于跑道，忽略跑道的坡度φ、飞机停机迎角αG和发动机安装角ψF等因素。根据牛顿第二定律可以得到飞机三点滑跑方程：

(1)

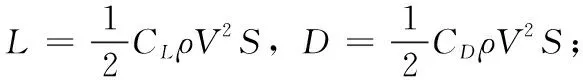
F为滑跑过程中地面和机轮之间的滚动摩擦力，F=fN。

图3 滑跑阶段中各力随速度的变化曲线

将各个参数代入式(1)得到：

(2)

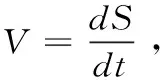
(3)

式(1)，(2)，(3)空气动力学方程中的V为真空速，而计算地面滑跑距离使用的是地速，因此在进行滑跑距离计算的时候，我们要将真空速转换为地速，联立式(2)和式(3)于是可以推导得出飞机的起飞地面三点滑跑距离为：

(4)

从式(4)我们可以看出，影响飞机起飞滑跑距离和滑跑时间主要有以下因素：起飞质量、襟翼状态、跑道状态和环境因素(温度和风速)等。上式有3个未知参数f、CL和CD，令A=S(CD-fCL)，则待辨识未知参数变为f和A两个参数。

1.3 起飞性能辨识模型

将起飞滑跑过程分为足够多的小段，每一小段均可视为匀加速过程，则由式(2) 可得速度增量为:

(5)

式(5)中，q为前一次观测的动压，Δt为观测时间间隔。

用θ1，θ2表示待辨识的两个参数，U作为输入量，则式(5)可以化为：

ΔV=C0+C1θ1+C2θ2U

(6)

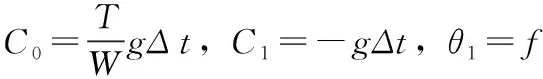
将式(6)进行变形得到形如：Y=τA的状态方程：

(7)

采用实数编码，辨识误差指标取为输出量Y的真实值和辨识值的方差：

(8)

其中，N为起飞抬前轮前辨识数据的数量，yi=Y(i)。

2 基于PSO算法的起飞阶段参数辨识

2.1 起飞数据采集及处理

我们使用的某型飞机飞行训练中快读存取记录器(QAR)中记录的实际数据，但飞行数据记录器上记录的数据我们并不能直接使用，在使用之前我们要进行预处理。数据预处理主要有野值剔除、数据填充和滤波。数据进行预处理目的就是为了准确地得到与飞机起飞相关的参数以便于准确可靠的利用PSO算法辨识参数确定起飞性能。与飞机起飞性能相关的参数包括: 飞机起飞质量、起飞襟翼度数、大气温度、机场气压高度、风速、指示空速、水平滑跑距离、挂弹情况、发动机转速和起飞松刹车信号等。取飞机起飞时实际状态 ( 起飞质量52 120 kg，起飞襟翼 22.3°，大气温度24.1℃ 机场高度423 m，逆风风速4 m/s，挂1枚炸弹) 的指示空速预处理结果如图4所示。

图4 预处理后的指示空速

2.2 PSO参数辨识

在预处理后数据基础上，本文采用PSO算法对起飞模型进行参数辨识，步骤[20]如下：

(1)将指示空速转换成地速，选取松刹车之后抬前轮之前的辨识数据段，将飞行速度随时间的变化转换为速度增量随时间的变化并作为观测量，建立数据文件

(2) 根据机场环境、飞机参数和发动机参数，计算与之对应的发动机推力和大气密度。

(3)选取待辨识参数的迭代初值。在起飞地面滑跑过程中，有关参数的取值范围为：摩擦系数：f=0.03-0.05，A=5-20；利用PSO进行辨识之前，我们要给两个待辨识参数一个范围，因此我们给的范围要大于参数取值范围。

(4)取粒子群个数为Size=50，最大迭代次数G=100，粒子运动速度为V=[-1,1]，取局部学习因子c1=1.3，全局学习因子c2=1.7，采用线性递减的惯性权重从0.90到0.10。

(5)将辨识误差指标J作为PSO的目标代价函数，进行迭代计算。最终使辨识参数经过100代迭代后收敛于一个合理、可信的结果。算法流程图如5所示。

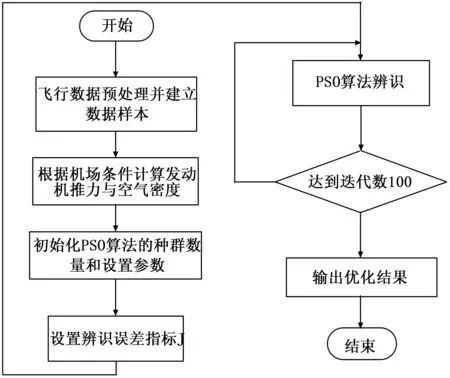
图5 PSO辨识流程图

经上述步骤，利用PSO我们辨识得到我们需要的两个参数结果分别为：f=0.0458和A=14.5832

辨识误差函数J的变化如图6所示。

图6 辨识误差函数J的优化过程

将辨识得到的两个参数代入式(2)，经过数值积分计算得到在三点滑跑距离如表1所示。另外，通过判读飞参记录器所记录的松刹车和抬前轮时刻的经纬度，可以解算实际的滑跑距离如表1所示。

表1 起飞参数辨识结果

从表1可以看出，经过辨识后计算出的飞机滑跑距离为294.076 m，通过查看实际数据发现上述参数分别为287.458 m。相对误差率为2.30%，满足工程使用要求。说明使用PSO算法对起飞阶段参数辨识有着很好的使用效果。

3 飞机起飞性能分析

为了进一步研究飞机三点滑跑的性能，分别用上述算法过程，采取了该型飞机在三个不同地区机场的起飞飞行数据，分析了不同温度和起飞重量和温度与起飞重量同时变化时三点滑跑距离。

3.1 温度对起飞性能的影响

飞行训练过程中，温度越高，滑跑距离越长；温度的变化直接影响发动机的推力，温度的变化也会使得空气密度发生变化。温度的升高使得发动机推力减小，空气密度减下，使滑跑距离增加，飞机性能变坏。在其他参数不变的情况下[18]，温度对发动机的推力影响为:(T0/T)2=R/R0，温度对空气密度的影响为：ρ=ρ0×(P/P0)×(T0/T)。

其中：T0为海平面标准大气温度的推力；R0为海平面标准大气下的推力；T为实际温度；R为实际温度时的推力。

利用PSO参数辨识方法，选取了该型飞机在三个不同机场的飞行数据进行辨识，得到三个f和A，然后代入式(1)计算滑跑距离，并进行修正使得误差满足工程精度要求。将辨识的f和A作为已知参数，把温度作为直接变量，将温度的变化转化为发动机推力P和空气密度ρ的变化，得到三个机场飞机三点滑跑距离如图7所示。

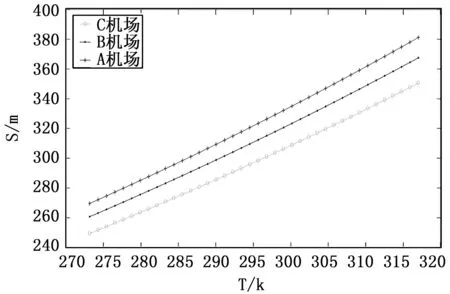
图7 不同温度下三点滑跑距离

从图7可以看出，三个机场的飞机起飞滑跑距离随着温度的增加而变大，说明温度是影响滑跑距离的重要因素。如图7所示，机场飞机起飞滑跑距离曲线随温度的增加而增加，近似呈线性关系，当机场温度在0°至45°度之间变化时，起飞滑跑距离变化的区间为240到380;对比不同机场的数据可以发现，在相同温度条件下，飞机滑跑距离从小到大依次为：A机场、B机场和C机场，作者查看了三个机场的地理位置发现，三个机场的海拔高度依次为 A机场、B机场和C机场。我们做了从飞机0°到最高温度45°的滑跑距离变化。如表2所示：

表2 温度变化下滑跑距离的变化情况

从表2我们可以看出三个机场温度在45°时的滑跑距离远大于0°，且A、B、C三个机场从0°到45°的增长率分别为40.47%、40.93%、41.35%，这个增长率说明飞机在地面滑跑温度为45°时要比0°时多40%的滑跑距离，这对机场跑道要求很严格，有可能跑道长度不够，飞机无法起飞。

3.2 起飞质量对起飞性能的影响

通常情况下，起飞重量越大，滑跑距离越长；飞机起飞重量W越大，飞机的起飞加速度必然减小；另外起飞所受重力增大使得飞机地面滑跑时的地面摩擦力增大。以上导致飞机抬前轮速度增大，滑跑距离变长，起飞性能变差。

利用PSO算法辨识出来的三个机场的f和A代入分别代入式(1)，将起飞重量W作为直接变量，得到滑跑距离如图8所示。

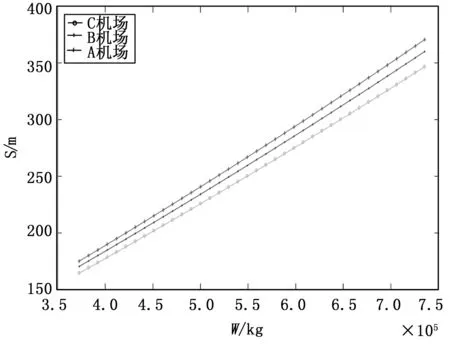
图8 不同起飞质量下的三点滑跑距离

从图8可以看出，3个机场的飞机随着起飞重量的增加，滑跑距离增加，说明起飞质量也是是影响滑跑距离的重要因素。3个机场起飞滑跑距离曲线随起飞质量的增加而增加，呈近似线性关系，当起飞质量在空载至最大起飞质量之间变化时，起飞滑跑距离变化的区间为150到380；在相同起飞质量条件下，飞机滑跑距离从小到大依次为：A机场、B机场和C机场。本文做了在温度为25°时飞机从空载到最大起飞质量的滑跑距离变化。可以得到三个机场飞机起飞质量从空载到最大起飞质量分别增加的情况如表3所示：

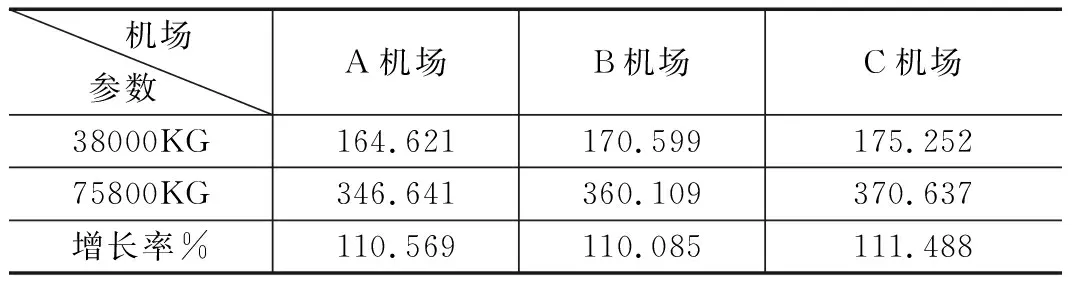
表3 起飞质量变化下滑跑距离的变化情况

从表2我们可以看出3个机场的飞机从空载到最大起飞质量滑跑距离增长率分别为110.569%、110.085%、111.488%，这说明了起飞质量对滑跑距离影响甚大，在保证安全完成任务的条件下要合理加注燃油使得飞机性能最佳。

3.3 温度和起飞质量同时变化下对起飞性能的影响

前面研究了在单一条件起飞质量或者温度变化的情况下对滑跑距离的影响，我们进一步研究两个条件下同时变化下滑跑距离的变化情况。图9是在两个影响因素共同作用下飞机的滑跑距离变化情况。

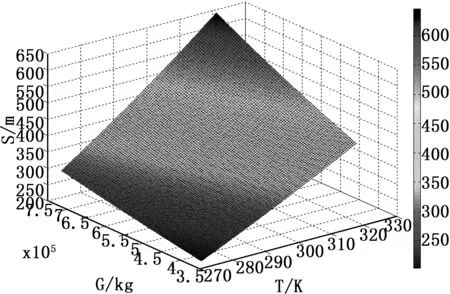
图9 温度和起飞质量同时变化作用下的三点滑跑距离

从图9可以看出在温度和质量同时增加的情况下，要大于单一温度和质量增加条件下的滑跑距离，这是由于在两个因素都增加的条件下，飞机推力减下，加速度减小，抬前轮速度增加，滑跑距离增长，飞机性能变差。在三维坐标轴上以温度和起飞质量坐标的平分线滑跑距离变化率最大。最大滑跑距离为647.464 m,对于比0°空载重量时滑跑距离203.066 m增长了218.839%，如果要安全起飞就要求滑跑距离要增大两倍多，在现有的机场下是不能起飞的。可以根据图9的仿真在机场实际的温度条件下最优化的加注相应质量的燃油，完成作战任务。

4 结束语

本文针对某型战机的起飞三点滑跑阶段进行了动力学建模，采用PSO算法利用经过预处理之后的飞参数据对模型中未知的两个参数进行辨识，结果表明PSO算法可以快速、准确地辨识出起飞性能所需的参数，并具有较高的精度。其次，我们用PSO算法辨识了3个不同机场的这两个参数，采用已辨识的参数代入模型分析了在不同起飞重量、温度条件下的三点滑跑距离，得到了单变量极限条件下滑跑距离；最后把温度和起飞重量，得到了双变量极限条件下滑跑距离。可以对决策者提供了战机出动参考策略，在平时的训练任务中可以选择在机场实际的温度下，结合训练任务，选择最佳的加油质量和挂导弹情况下满足飞机起飞条件，完成最佳的训练任务。在今后的飞机起飞性能数据分析中应进一步推广，并应探索将其应用到其它性能分析中的方法。