舰载机弹射起飞安全性的影响因素分析

董阿鹏, 李书, 朱文国, 吴伟潇

(北京航空航天大学航空科学与工程学院, 北京 100083)

舰载机的起飞方式是衡量其作战水平的重要技术指标，与滑跃起飞方式相比，弹射起飞具备更高的弹射效率、更大的弹射重量等优点。蒸汽弹射起飞是指利用高温高压水蒸气为动力，在航母宝贵的甲板范围内，借助弹射器，将舰载机在短时间内加速到要求速度而离舰起飞。目前，运用范围最广，时间最长，已得到飞行实践验证的起飞方式就是蒸汽弹射起飞方式。

在复杂海洋环境下，舰载机弹射起飞过程，舰船、弹射器、扭力臂、轮胎、缓冲支柱和机体等可活动部件存在约束和运动耦合关系，是一个典型的多体系统、多学科交叉的动力学过程，系统建模是一个较为复杂的问题。首先，由于舰载机是相对于航母这样一个运动平台起飞，受海浪影响，航母的摇荡运动会对舰载机的运动带来牵连速度和加速度；其次，在弹射过程中，起落架缓冲支柱和机轮轮胎受力变形，在甲板上振荡，相互影响，时刻改变飞机姿态以及各力元大小；另外，舰载机还会受到海面大气紊流、舰艏上洗流和地效丧失等因素影响。这些因素很大程度上影响舰载机的起飞性能，带来一定的安全风险。

英国、美国、法国等对弹射起飞过程的研究较为成熟，但可参考的资料较少，研究内容主要涉及弹射起飞安全性准则的制定方面[1-5]。目前，中国关于舰载机弹射起飞的研究关注点主要集中在以下几个方面：外部环境对起飞特性的影响[6-7]，蒸汽弹射原理与仿真[8-9]，减震支柱的力学行为[10-12]，机舰适配性[13-14]，动力学建模策略[15]以及飞行控制系统设计[16]等方面。研究主要是对弹射起飞的规律性认识为主，所建立的模型大大简化，存在一定的局限性。首先，不考虑蒸汽弹射系统的热力过程(以理想化的弹射力代替)，起落架作为简单的质量弹簧模型对待，仅仅围绕着舰载机质心动力学展开；其次，所建模型难以模拟舰船运动对空气流场的影响、舰船不同方向耦合运动对弹射过程的影响(认为舰船运动的耦合效应只是单一方向的线性叠加)；另外，由于刚体数目众多，不同刚体之间质量特性相差大，研究者们往往专注于弹射过程舰载机的姿态安全问题，忽略了弹射机构各构件的受力分析，模型不够完整；最后，虽然近年来多体动力学理论逐渐被应用于弹射动力学的分析[17-18]，但均是在相对坐标系欧拉法描述，大量的广义坐标、超越函数以及转换矩阵往往使分析过程过于复杂，模型精度差、效率低。因此，建立一个高效完整的动力学仿真模型是非常必要的。

利用自然坐标法建立多体系统模型具有很多的优点，例如完全由笛卡儿坐标描述而无需坐标转换，质量矩阵为常数，约束雅可比矩阵为线性，具备较高的求解效率等[19]，然而由于其非传统的建模观念，自然坐标法至今未能在学术界和工业界得到足够的重视，研究兴趣主要集中在生物力学领域[20-24]，在复杂动力学系统建模方面鲜有报道。本文首次在绝对坐标系下，采用自然坐标法，在考虑蒸汽弹射器动力过程的基础上，统一完整地建立了舰载机弹射起飞多体系统动力学模型，较为全面地反映了弹射过程不同模块之间的耦合关系。在此基础上，结合弹射过程仿真曲线，从舰载机水平加速度以及飞行轨迹下沉量2个维度量化分析了舰载机弹射起飞系统各参数对起飞安全性的影响规律，为舰载机弹射起飞系统的设计提供一定的参考。

1 弹射起飞系统

弹射过程一般分为准备阶段、弹射起飞阶段、

自由滑跑阶段、自由飞行阶段，不同阶段系统具备不同的边界条件以及运动方式。舰载机相对舰船达到准平衡状态之后，弹射阀打开，弹射杆载荷按一定的速率增加，当定力栓达到临界载荷被拉断后，飞机在弹射拖梭的牵引下加速滑跑，弹射气缸行程达到最大时，拖梭与弹射杆脱离，舰载机进入自由滑跑阶段，随后主轮冲出甲板，舰载机离舰进入自由飞行阶段。

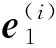
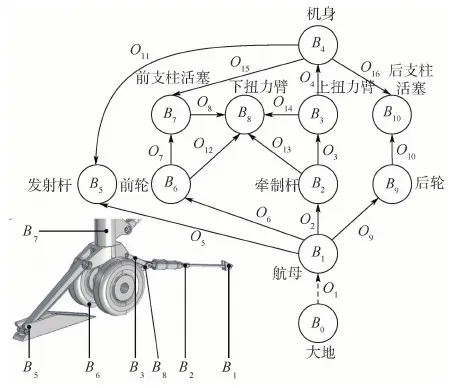
图1 多体起飞弹射系统的拓扑结构Fig.1 Topological structure of multi-body catapult launch system

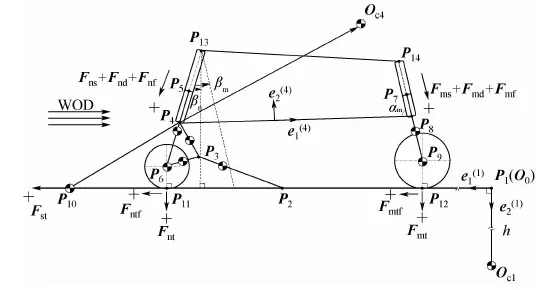
图2 多体起飞弹射系统示意图Fig.2 Schematic diagram of multi-body catapult launch system

2 动力学模型

2.1 舰船运动模块

根据随机过程理论，海浪的运动是平稳的，是具备各态历经性的随机过程，不同海况对应不同的功率谱密度函数，舰船的运动可看作一个线性系统在已知海况功率谱输入下的随机响应问题。在工程实践中，为了便于分析，针对不同类型的舰船及其设计准则，可以近似采用简谐波的形式来表征舰船在不同海况下的运动情况。本文舰船运动模型为纵摇1.5°，周期6 s，垂荡2.5 m，周期12 s，两方向的初相位由它们之间耦合状态选定。航空母舰前进速度为15 m/s。

2.2 弹射系统模块

从系统工程学的角度看，蒸汽弹射器的动力特性应该包含在分析模型之中，而不应该以既定的、理想化的力学函数来近似代替，并且，完整的数学模型可以对弹射器的设计与控制提供参考。为了简化弹射力的计算，本文做如下假设：工质为干饱和水蒸气，与外界无传热；热力过程为准静态过程，忽略蒸汽的机械能以及容器变形。

舰载机在弹射过程中作匀加速运动是最理想的运动规律。舰载机的加速特性由弹射力大小决定， 基于以上假设，弹射力大小由蒸汽流量唯一确定，控制蒸汽流量就可以控制弹射力的输出大小。可假定阀塞纵剖面的轮廓线为二次曲线，且阀塞匀速提起，蒸汽流通面积即为时间的一次函数[8]。

2.3 气动模块

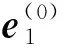
(1)

式中：xh为全机气动中心距舰艏的水平距离；e1-2为从基点P1至基点P2的单位向量。根据海况等级可采用幅值0.5 m/s，周期为1 s的简谐波的形式与甲板风相加来近似模拟湍流脉动的影响。除此之外，舰载机冲出甲板进入自由飞行的瞬间，地效的突然丧失不仅会改变舰载机的气动俯仰力矩而且也会明显降低升阻比，增加弹射起飞的安全风险。工程实践中，关于地效对气动力系数的影响存在可靠的数学模型以供参考[25]。

2.4 起落架模块

双腔油气式缓冲器因其高效率和高功量吸收能力而被普遍应用于现代飞机上，本文前后起落架均采用双腔油气式，其主要参数如表1所示。

表1 起落架缓冲器主要参数Table 1 Main parameters of landing gear buffer module

注：停机行程比为0.56； 活塞面积为0.02 m2； 阻尼面积比为0.015; 停机-全伸压缩比为3。

其中，起落架外筒视为是机身的一部分，气簧缓冲过程为等熵变化过程，油液流动忽略位能，满足伯努利方程，摩擦力是轮胎支反力和活塞杆上下支点距离的函数，方向与油液阻尼力相同。

2.5 多体模块

2.5.1 刚体描述

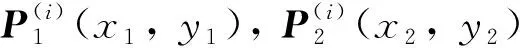
(2)

式中：i为刚体编号，0号刚体为地球。则刚体质心在绝对坐标E0(O0,e1(0),e2(0))下可表示为

ρc(i)=Diqi

(3)

其中：Di为刚体质量分布矩阵，由牛顿第二定律可得到刚体平移微分方程：

(4)

式中：mi和Fi分别为刚体质量和外力列向量。同样，刚体的角速度可以利用自然坐标的时间变化率来表示：

(5)

其中：Gi为角速度转换矩阵，由角动量理论可得到刚体转动微分方程：

(6)

式中：Ji为刚体中心转动惯量；Mi为外力矩列向量。

2.5.2 约束方程

一个刚体存在3个自由度，4个自然坐标意味着需要额外补充一个刚体约束，既两参考点构成的向量二范数恒为初始值。由于本文中前后轮胎B8、B10被视为柔体，故需要解除两者约束。

(7)

式中：li为i号刚体基点之间的距离。除了刚体本身的完整约束以外，各个刚体之间的铰约束也是求解动力学问题的必要条件。如前所述，起落架外筒被视为机身一部分，针对机体B4需要多选取俩参考点P13、P14来构造机体的起落架方位，故前后起落架支柱与活塞的棱柱铰约束可表示为

(8)

式中：C1、C2为任意常数。铰约束的增加必然带来刚体本身的位形约束，需要为机身补充如下4个完整约束，对于舰船的多余参考点Oc1，用同样的方式处理。

(9)

式中：Lms和Lns分别为主支柱和前支柱的长度。由于自然坐标法的特性性质，除舰船运动的非定常约束外，刚体的约束方程均为定常完整约束。同时，模型中还存在4处非完整约束，即前后起落架缓冲行程边界的约束以及前后轮胎与甲板接触点的约束。对于前者，可以采用伺服控制的方法，通过对气簧力乘以一个增益因子来限制活塞行程，对于后者，可通过几何关系的约束来实现。

(10)

式中：C3、C4为任意常数。整个弹射系统包含14个刚体约束方程(舰船3个，机体5个，其余刚体各1个)，4个柔性体约束(前后轮胎各2个)，5个棱柱铰约束(4个起落架棱柱铰约束与1个弹射器棱柱铰约束)以及在不同方向上舰船位移的3个非定常约束，总计26个约束条件。求解时，舰载机弹射起飞过程也是约束方程数不断减少的过程。

2.5.3 系统动力学方程

采用拉格朗日乘子法构建系统动力学方程式的约旦形式：

ΦqTλT]=0

(11)

式中：m、J、D、G和Φq分别为系统刚体质量阵、转动惯量阵、质量分布阵、角速度转换阵和约束雅可比阵；q、λ、F和M分别为自然坐标列阵、拉格朗日乘子列阵、各刚体合力和合力矩列阵。从而，弹射动力系统的微分代数方程可以转化为以下形式：

(12)

式中：A、B和ζ分别为系统装配后的质量阵、外力列阵和约束条件的二阶变分余项。

3 仿真与讨论

影响舰载机弹射起飞的安全因素主要包括起飞重量(W=42 t)，弹射阀开启速率(a=0.003 m2/s)，发动机推力(T=2×125 kN)，定力栓临界力(f=400 kN)，剩余甲板长度(d=5.5 m)以及舰船不同方向的耦合运动等参数。在下文的讨论中，当甲板静止时，0～3.5 s时间是舰载机建立相对甲板准平衡的过程，3.5 s弹射阀打开时刻，12 s仿真结束。除特殊说明外，所有相关参数均取括号中的默认值，以方便对比分析。本文主要从舰载机质心水平加速度ax以及离舰下沉量sz两方面来界定安全起飞条件，即在弹射滑跑过程，ax<5g，离舰后ax>0.065g且sz<2 m。为了提高计算效率，在求解微分代数方程组时，采用四阶单步隐式Runge-Kutta法启动，四阶四步Adams法推进的计算方法。

3.1 起飞重量

从图3(a)中可以看出，舰载机水平方向呈分段匀加速运动状态，这说明弹射阀流通面积线性增加的控制策略是合理的，弹射滑跑阶段，起飞重量与水平加速度呈线性变化关系，质量越小，加速度越大(最大5.1g)，弹射历时越短，而离舰起飞段，随着起飞重量的增加，加速度呈减小趋势(最小0.4g)，同时，离舰后的飞行航迹随着起飞重量的增加逐渐外倾，并开始出现一定程度的下沉(最大2.5 m)，如图3(b)所示。很明显，对于给定参数，最大起飞重量处于32～42 t之间是安全的。

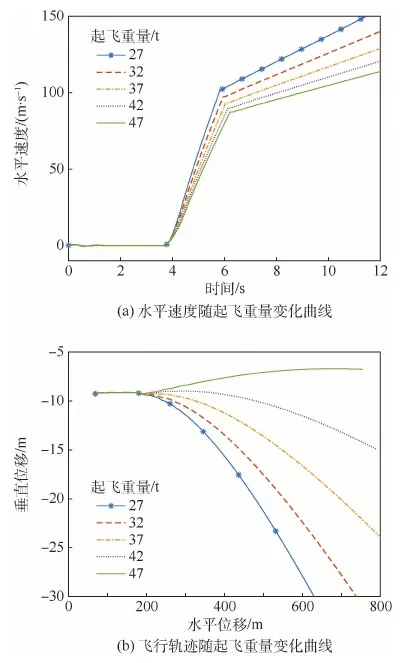
图3 起飞重量对水平速度与飞行轨迹的影响Fig.3 Effects of takeoff weight on horizontal velocity and flight trajectory

3.2 起飞动力

3.2.1 蒸汽弹射力

图4给出了5种弹射阀开启速率下，舰载机水平速度以及飞行轨迹曲线。如图4所示，随着弹射阀开启速率的降低，弹射滑跑时间有所延长，末端速度明显减少，离舰时的升力不足以平衡自身重力，导致飞行轨迹下沉，对飞行安全不利。因此，在保障舰载机弹射安全的前提下，根据待弹飞机参数，精确控制弹射阀开启速率a非常关键。从图中可以看出，对于选定的弹射参数，a取0.001～0.002 m2/s航迹下沉过大(>2 m)，a取0.005 m2/s时，弹射过程纵向加速度过高(>5g)，均不符合安全准则要求，而a取0.003～0.004 m2/s较为合适。

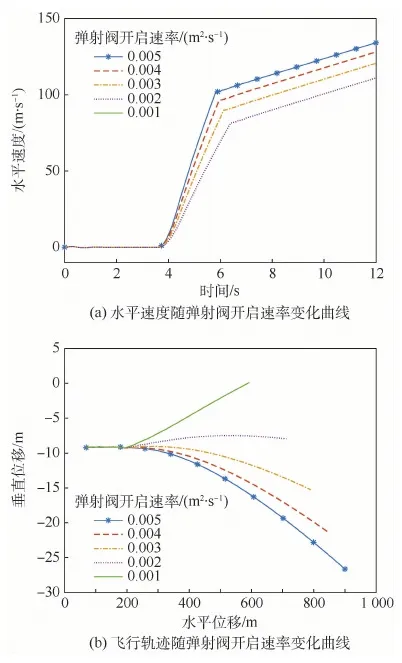
图4 弹射阀开启速率对水平速度与飞行轨迹的影响Fig.4 Effects of opening rate of catapult valve on horizontal velocity and flight trajectory

3.2.2 发动机推力

不同发动机推力对水平速度以及飞行轨迹的影响曲线如图5所示。与弹射阀开启速率对舰载机加速性能的影响有所不同，随着发动机推力的增大，舰载机在弹射滑跑阶段，加速性能并没有很大改变，这说明舰载机加速起飞所需的外力主要来自于蒸汽弹射器，发动机推力所占比例较小。另外，随着发动机推力的增加，离舰后飞行轨迹下沉量有所减少，水平加速度与爬升率大幅提升，这对飞行安全是非常有利的。从图5中可以看出，5种发动机推力均能够安全起飞，但考虑到飞行安全的裕度，弹射性能的优化以及驾驶员的心理感受等因素，在现有推进技术水平下，大推力发动机仍是首选。

图5 发动机推力对水平速度与飞行轨迹的影响Fig.5 Effects of engine thrust on horizontal velocity and flight trajectory

3.3 母舰约束

3.3.1 定力栓临界值

定力栓临界值决定着舰载机开始滑行时弹射器气缸内蒸汽的状态。如图6所示，随着临界值的增大，弹射开始时刻有所延后，加速度略微增加，但随着弹射的进行，舰载机的加速性能彼此差异不大，离舰速度小幅提升，离舰下沉量有所减少。另外，从图6中可以看出，尽管f对飞行轨迹影响很小，其对弹射系统的结构振动的影响却不容忽视，f的大小很大程度上改变了弹射开始时刻气簧力的振动幅值和相位，而且存在一个最佳的临界值使得结构振动最小(f=500 kN)。

总体来说，在弹射历时变化不大的情况下，增加定力栓临界值可以一定程度上提高舰载机离舰速度，从而降低了舰载机离舰后的下沉量，但此过程需要兼顾其对系统带来的激励和时延效应。

图6 定力栓临界值对水平速度、前支柱气簧力与 飞行轨迹的影响Fig.6 Effects of critical value of fixed-load plug on horizontal velocity, nose-strut spring force and flight trajectory

3.3.2 剩余甲板长度

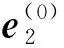
如图7所示，在自由滑跑阶段，当前轮离开甲板后，主轮的支反力提供额外的低头力矩，使升力Lx大小有略微减小，随着d的减少，这种变化变的愈加明显，这与前轮突伸的完成程度有关，前支柱势能在甲板上的充分释放必然会使离舰之前的升力曲线更为平滑。当全机气动中心冲出甲板后，由于地效的丧失，升力骤然降低，在俯仰、阻尼力矩的作用下，升力呈波动状回升。另外，从离舰轨迹中可以看出，航迹下沉量对d值较为敏感，在自由滑跑阶段，剩余甲板长度直接影响到离开甲板前质心的升高度以及升力的储备量，这对离舰后的飞行轨迹影响很大。

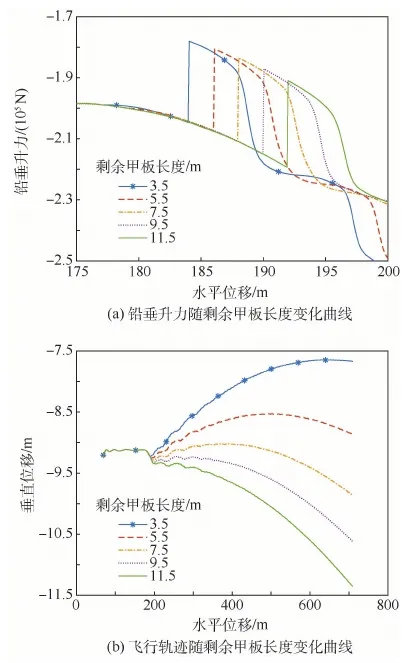
图7 剩余甲板长度对铅垂升力与飞行轨迹的影响Fig.7 Effects of deck edge distance on vertical lift and flight trajectory

另外，在设计剩余甲板长度时，既要考虑到离舰下沉量的影响，同时也必须考虑到航母工程造价，在满足安全准则的基础上，剩余甲板长度应尽量短一些，一般d不超过10 m。从分析可以得出，对于该组参数的舰载机，5种剩余甲板长度均可安全弹射起飞，但d取5.5～9.5 m是可行的。

3.3.3 舰船运动

舰船垂荡与纵摇运动对舰载机的飞行安全有很大影响，两者的不利耦合使情况进一步恶化。在舰载机离舰时，舰艏的运动有两种最不利的运动状态，即下沉位移最大和下沉速度最大。由于舰船存在两个方向的位移，所以可通过分析离舰时刻垂荡位移最大或速度最大与纵摇位移最大或速度最大之间的4种极端耦合行为来考察，如图8所示。为便于说明问题，此处起飞重量W=37 t，弹射阀开启速率a=0.005 m2/s，其余参数取默认值。

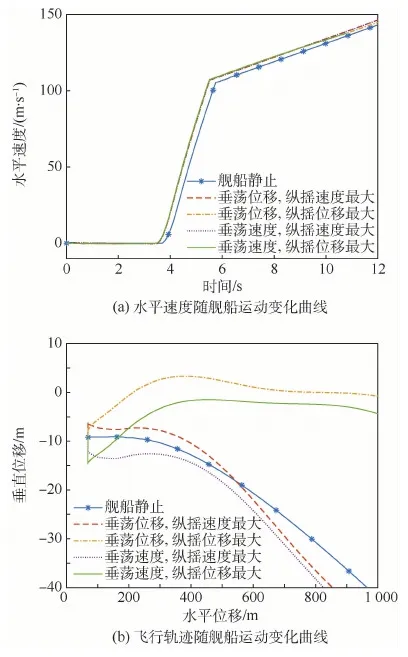
图8 舰船运动对水平速度与飞行轨迹的影响Fig.8 Effects of carrier motion on horizontal velocity and flight trajectory

如图8所示，舰船运动时，两者均呈现明显的耦合性质，从航迹曲线中不难发现，纵摇是航迹下沉的主要原因，垂荡运动只是在小范围内平移了曲线，变化趋势并没有明显改变。除此之外，甲板的运动的动载荷使拉断栓提前到达临界值，加速度曲线向左平移了约0.4 s，而加速度值无明显变化，但均超过了5g，不符合安全要求。由此可见，对应于该型舰载机弹射参数，当舰船在纵摇位移最大时，尽管弹射加速度超出了弹射起飞安全允许值，但其下沉量仍然不满足安全要求。单一要素的优化不是有效控制下沉量的措施，需要综合分析各要素的影响。

4 结 论

1) 对舰载机弹射起飞系统作了详细的分析，首次在绝对坐标系下，利用自然坐标方法建立了弹射起飞多体系统模型，完整考虑了弹射过程中各模块相互耦合对弹射起飞过程的影响，具有较大的理论和实际意义。

2) 起飞重量、弹射力大小以及发动机推力对舰载机弹射过程中的水平加速度均有所影响，但不同弹射阶段主要影响因素不同。定力栓临界值对飞行轨迹和加速度影响都不大，但对结构振动的影响却不可忽视。较大的剩余甲板长度可有效提升离舰时的升力，但应考虑经济因素。航母不同方向的耦合运动对飞行安全构成很大威胁，需避免最大纵摇时刻离舰起飞。需要注意的是，在确定最佳弹射时间时，应考虑舰船运动以及定力栓临界值的变化两者导致的弹射时间的时延效应。

影响弹射起飞安全的因素包含很多其他因素，例如俯仰角速度，飞行迎角以及舵面偏度等，本文只是从水平加速度与航迹下沉量2个方面，通过选取主要飞行参数对弹射起飞安全性进行了讨论，存在一定的局限性。另外，虽然本文基于系统工程的建模思想，模型集成多个子模块，但舰载机的横测向力学问题并未考虑，因此，三维模型的建立将成为下一步的工作。