基于多目标优化与强化学习的空战机动决策

杜海文, 崔明朗, 韩统, 魏政磊, 唐传林, 田野

(1. 空军工程大学航空工程学院， 西安 710038； 2. 94782部队， 杭州 310004； 3. 福州大学物理与信息工程学院， 福州 350108)

随着无人机技术的不断发展，无人作战飞行器(UCAV)的作用与地位也在不断升高，在战场上的意义越来越重要[1]；由于不必考虑人身体条件限制，UCAV可以完全发挥出飞行器的性能，做出有人机难以做出的大过载机动，可以预见UCAV必将成为未来空中战场的主角。而要实现高强度的空中对抗，UCAV必须脱离地面控制，具备自主空战的能力，本文结合传统优化模型以及机器学习方法，建立了基于多目标优化的机动决策模型，用于解决UCAV自主空战时的机动决策问题。

关于空战机动决策问题有很多研究成果(包含有人机与无人机)，总的来说大致可以分为3类：①基于各类基本战术动作库的机动决策，文献[2]最早对建立机动动作库进行了系统的研究和总结，文献[3-4]分别就机动动作库的设计、控制应用以及基于动作库的机动动作识别等问题进行了研究，详细阐述了基于动作库的机动决策中存在的各类问题。②基于优化方法的机动决策，该类方法的共同点在于通过各类态势评估方法将机动决策问题转化为标准的优化模型，文献[5-6]基于各类不同的智能算法来求解优化模型，文献[7]基于各类态势分析方法建立了隐马尔可夫模型，并使用维比特算法进行求解。③基于机器学习方法的机动决策，机器学习方法研究在近年得到了极大的发展，采用各类机器学习方法研究机动决策也越来越多，文献[8]应用深度置信网络来进行态势评估，文献[9]采用了强化学习方法研究空战智能决策。

然而，以上方法在处理无人机空战机动决策时都存在一些弊端：机器学习方法在处理类似对抗博弈问题时效果很好，但不同于有人机的空战决策，无人机空战基本不存在有学习价值的样本；而各种基于动作库的方法虽然是建立在大量空战经验之上，但灵活性较差，且现在的空战经验都是有人机的经验，无法确定其用在无人机上是否可靠。相比之下，传统的优化方法原理是基于对态势分析的寻优，反而可以根据不同的飞行器性能和空战环境得出实时性与灵活度都较强的决策，但是传统优化方法在整合不同态势参数时缺少严谨的方法，且其决策结果随着模型的确立就已经确定下来，无法体现出对抗博弈的思想。基于上述分析，本文依然使用优化模型作为决策的核心思想，采用多目标优化方法取代单目标优化，并通过强化学习方法建立辅助决策网络，建立了具备实时对抗性的无人机空战机动决策模型。

1 机动决策模型

1.1 UCAV运动模型

在对UCAV近距空战进行机动决策与仿真时，采用三自由度质点模型描述UCAV的运动状态，模型参数定义如图1所示。

图1 UCAV三自由度质点模型Fig.1 UCAV three-degree-of-freedom particle model

1.1.1 模型假设

对建立UCAV运动、动力学模型作如下假设：

1) 假设UCAV为一个刚体。

2) 假设地球为惯性坐标系(将地面坐标系看作惯性坐标，忽略地球自转及公转影响)。

3) 忽略地球曲率。

1.1.2 UCAV质点模型

在考察UCAV运动时，将UCAV视为质点。在惯性坐标系下，其质点运动方程为

(1)

相同惯性坐标系下，UCAV的质点动力学方程为

(2)

式中：vu为速度；γ为航迹倾角；ψ为航向角；μ为滚转角；α为迎角；m为质量；T为发动机推力；D为空气阻力；L为升力；g为重力加速度。

飞行过程中，UCAV所受升力L与空气阻力D计算公式如下：

(3)

式中：ρ为空气密度；S为UCAV参考横截面积；CL和CD分别为升力和阻力系数。

UCAV发动机推力T计算公式如下：

T=δTmax

(4)

式中：Tmax为发动机最大推力；δ为油门，取值范围为[0,1]。

在控制量的选择上，仿照有人机中飞行员的驾驶方式，采用迎角α、油门δ、滚转角μ三个控制量来控制UCAV进行机动。

1.2 多目标优化方法

基于优化方法的机动决策模型具有较高的决策效率与良好的实时性，但在寻优过程中需要对多个目标参数进行合并，这样的合并过程往往使用层次分析法、专家打分法等主观性较强的方法来确定权值，缺少严格的证明过程，其决策结果难以使人信服。

事实上，在不同的空战环境下，对于各个态势参数的需求程度也是不同的，所以将不同态势参数加权求和后进行优化的方法本身就具有很大的局限性。为了避免这种局限性，本文结合多目标优化思想，建立了多目标优化机动决策模型。

1.2.1 多目标优化思想

首先简要介绍一些多目标优化问题中的概念，在多目标优化中，采用Pareto支配[10]关系来判断解的优劣程度，Pareto支配关系的定义如下。

定义1对于可行域内任意2个解x1与x2，假设在最小化问题f(f1,f2,…,fk)中，当且仅当式(5)成立时称x1对x2形成Pareto支配：

[∀i∈{1,2,…,k},fi(x1)≥fi(x2)]∩

[∃i∈{1,2,…,k},fi(x1)≥fi(x2)]

(5)

x1支配x2表示解x1优于解x2，一般记作x1≻x2。

由定义1可知，求解多目标优化问题的本质就是在全部可行解中找到所有不被任何一个其他可行解所支配的解的集合。将这个集合称之为多目标优化问题的Pareto边界，具体定义如下。

定义2设多目标优化问题f的可行解集为X，则其Pareto边界为

(6)

多目标优化的目的就是求出优化问题的Pareto边界。

1.2.2 优化目标

使用优化模型必然需要构建优化目标参数，采用速度、高度、距离、角度[11-12]4个量作为优化目标是最为常用的方法之一，但这些量的具体战术意义还不够明确，本文将基于空战实际将这些参量进行耦合后提出了如下优化目标参数。

1) 基于武器攻击区的威胁参数

空战的最终目的就是击落敌方与保护己方，进行机动也正是为了使己方构成武器发射条件和避免使对方构成武器发射条件，故本文基于机载武器攻击区的概念，结合与之相关的角度、距离等常规评估参数，提出了一种新的威胁参数ηA作为一个优化目标，参数模型以双方携带弹药类型为基础，具体定义如下。

① 常规条件下。制导武器一般以空空导弹为主，现在的空空导弹的攻击区大致如图2所示。

假设图2中攻击区为我机携带的第i枚导弹的攻击区，则该型导弹对敌机威胁参数为

(7)

式中：Rg为该导弹沿视线角αu方向上的最远攻击距离，由于部分导弹不具备全向打击能力，故若在当前αu下Rg为0，则定义此刻ηai=0。

图2 态势参数定义Fig.2 Definition of situation parameters

根据上述方法计算出我机携带所有空空导弹对敌机威胁参数(ηa1,ηa2,…,ηan)后，取其中的最大值ηamax，即为我机当前对敌机的威胁参数ηa；采用相同方法计算出敌机对我机威胁参数后，取两者之差即为总威胁参数值ηA：

ηA=ηa(ucav)-ηa(enemy)

(8)

② 仅使用非制导武器时。空对空作战非制导武器一般指航炮，由于航炮的发射条件比较苛刻，一般只在形成尾追时才能构成发射条件，故直接使用双方角度参数与距离参数进行耦合来定义其态势参数：

(9)

式中：Ra为航炮射程。

2) 能量参数

能量理论[13]是近期提出的一种空战机动理论，该理论的核心在于：在空战中首先寻求获得能量上的优势，然后将能量优势转化为态势上的优势。能量理论随着飞机性能的提升愈发受到重视，现在的飞机性能可以支持完成各种大过载机动、过失速机动等非常规动作，这使得飞机可以有更多方式扭转不利的态势。即使在常规的机动对抗中，能量也是一个不可忽略的条件，因为所有机动动作都是以消耗能量为前提，高能量就意味着更多的机会与选择。故本文设置能量参数ηW作为一个优化目标，计算公式如下：

(10)

式中：Wp和Wk分别为重力势能与动能；Wst为能量标准化参数；mu为我方UCAV质量。

1.2.3 多目标优化机动决策模型

决策模型结构如图3所示。

目前有很多种多目标算法可供使用，由于上述模型复杂度不高且机动决策对实时性有较高要求，考虑到灰狼算法在处理维数较低问题时收敛速度快，本文在仿真时采用多目标灰狼算法(MOGWO)[14-15]。

事实上，多目标优化模型具有良好的可拓展性，在实际应用时，可以根据实际空战环境在以上2种优化目标的基础上添加其他新的优化目标(如雷达性能、电子战等)，添加时只需将新的目标参数模型加入原优化目标集即可，不需要对决策模型中的其他结构进行任何变化。

图3 多目标优化机动决策模型结构Fig.3 Structure of multi-objective optimization model for maneuver decision

1.3 基于强化学习方法的辅助决策

1.2节提出了多目标优化思想并建立了优化参数的模型，但多目标优化模型仍存在以下缺点：

1) 多目标优化的结果是一个决策集，并没有给出从决策集中的选择具体决策的方法，如果不采用其他辅助决策方法，则只能从决策集中随机选取决策。

2) 多目标优化的本质依然是优化模型，未体现出空战博弈的思想。

强化学习方法[16]在处理类似的对抗博弈决策中取得了很大成果，但由于无人机空战决策问题的复杂度太高而难以实现。然而，如果在多目标优化的基础上进行强化学习，强化学习任务的探索空间将大大减少，故本文以多目标优化为决策基础，使用强化学习方法训练评价网络，用于对决策集中的决策进行评价与选择，从而解决上述2点不足。

1.3.1 蒙特卡罗强化学习

强化学习任务通常用马尔可夫决策过程(Markov Decision Process，MDP)来描述，任务对应了四元组E=，St为状态空间，是机器所感知到的环境描述的集合,Ac为系统能够采取的行为的集合,Pr指定了不同环境下采用各种行为的概率，用以在探索过程中为行为选择提供参考,Re指定了奖赏，通过反馈来调整Pr中的概率。

虽然对于空战中态势评估的研究已较为完善，但考虑到空战过程中机动动作往往是一系列的连续动作，即在完整的机动决策中，并非每一时刻都是为了追求最优态势。所以要设置符合要求的奖赏函数并不容易，而蒙特卡罗方法可以解决这个问题。

蒙特卡罗强化学习[17]的思路是采用多次“采样”求平均奖赏的方式来近似对行为的评价，即系统从起始状态下开始探索环境直至结束，将整个过程的奖赏作为过程中经历的每一个状态st的一次累积奖赏，在多次采样后，对每一个状态st的累积奖赏取均值得到其奖赏值re。

就效率而言，蒙特卡罗强化学习比其他强化学习方法相去甚远，在实践中对蒙特卡罗方法的应用也不是很广泛，但本文模型的决策核心还是多目标优化，强化学习任务只需对多目标优化的决策结果进行评价与选择，即强化学习的行为空间A为一个已经经过筛选的较小空间，故收敛速度必然大大提升，从而使蒙特卡罗方法具备了可行性。

1.3.2 基于神经网络的值函数近似

初始的强化学习方法都是针对离散的状态-动作空间来进行的，但对于空战而言，其状态空间与动作空间都是连续的高维空间，进行离散化处理显然不是合适的方法。在类似的高维连续空间强化学习中，往往采用值函数近似的方法来进行连续空间的强化学习。

值函数近似[18]指的是通过一个函数φ建立从状态St到状态奖赏值的映射:φ:St→Re。考虑到空战决策问题的复杂性，最终的近似函数必然是复杂非线性函数，而神经网络在拟合复杂非线性函数时具备较好的性能， Hornik等[19]在1989年就证明了只需一个隐层的BP神经网络可以逼近任何闭区间的连续函数，故本文将训练一个三层的BP神经网络来拟合值函数，用以对多目标决策集进行评价。隐层节点数将依照以下经验公式进行设计：

(11)

式中：lno为隐层节点数；nno和mno分别为输入和输出节点数；ano为1～10之间的调节常数。

结合对辅助决策网络功能的需求，网络具体设置如下：

1) 将空战态势(即状态量)作为输入层，利用si{R,αu,αe,Δh,Δv}5个参数来描述空战态势，即网络输入层节点数为5，Δh为两机高度差，Δv为速度差。

2) 网络输出为对输入态势下我机获胜期望的预测值ν([0,1]之间的数，ν值越大代表获胜期望越大)，输出层节点数为1。

3) 神经网络训练采用LM(Levenberg-Marquardt)方法，其中BP误差计算类似于时序差分(TD)方法[20]误差计算公式，但由于模型采用蒙特卡罗方法，只能使用每次仿真结果作为本次仿真所经历状态的统一奖赏值，具体计算公式如下：

(12)

式中：αRL为学习率，一般根据训练次数确定；γRL为折扣率，本文取γRL=0.4；r为奖赏值，r值由仿真结果rend给出，rend取值为0、0.5或1(对应失败、平局或胜利)；n为本次仿真经历的总步数；i为当前状态步数。

4) 结合隐层节点数经验公式，通过实际仿真效果，选择隐层节点数为12。

1.3.3 辅助决策模型

辅助决策网络的强化学习模型训练步骤如下：

步骤1初始化辅助决策网络。

步骤2随机产生敌我双方初始位置状态，开始仿真模拟。

步骤3记录下当前敌我态势关系sii，由多目标决策模型得出决策集(敌机可以采用与我机相同策略进行机动，或根据实际需求预先设置其轨迹)。

步骤4预测每种决策后敌我态势关系，进而通过辅助决策网络得出对应的获胜期望{ν1,ν2,…,νn}。

步骤5从决策集中随机选取出最终执行的决策，每种决策的被选取概率为

(13)

步骤6执行决策后判断是否达到空战结束条件，若未达到，返回步骤3；若已达到，进入步骤7。

步骤7对本次仿真所经历的所有状态si，通过式(12)计算BP误差返回辅助决策网络用于网络更新。

步骤8判断是否达到最大训练次数，若未达到，返回步骤2。

注意：训练过程中，若敌机采用相同的决策模型，则双方数据均可通过步骤7中的网络更新；若敌机采用预先设置好的其他机动方法，则只有我方数据可用于网络更新。

1.4 机动决策模型整体框架

结合1.2节和1.3节描述的多目标决策模型与辅助决策网络，机动决策模型整体框架如图4所示。

图4 机动决策模型结构Fig.4 Structure of maneuvering decision model

2 仿真实验

由于本文机动决策涉及模型较多，故在仿真时将针对各个模型予以验证，仿真环境及参数设置如下。

仿真时，敌我飞行器采用相同的参数，质量m=14 680 kg，参考截面积S=49.24 m2，高度限制为h∈[1,12] km，速度限制为v∈[80,400] m/s，迎角限制为α∈[-10°,30°]；发动机采用F-4涡喷发动机数据[21]，其最大推力采用式(14)拟合：

(14)

升力系数和阻力系数采用式(15)拟合[22]：

(15)

考虑到本文未针对探测能力设置优化函数，故训练时设置双方均只使用航炮进行近距空战(近距格斗时电子战作用较小，但对机动决策模型有较高要求)，所有仿真中决策步长为1 s；训练过程中，判定相互脱离距离为15 km；攻击条件设置为αu∈[-20°,20°]且R<2.5 km(参数定义见图2)，满足攻击条件3 s视为进行有效攻击；任意一方进行有效攻击或双方脱离则仿真结束。

仿真实验在Matlab 2013a下进行，运行环境为Inter(R)Core(TM)i5-2310处理器，3.40 GB内存。

2.1 多目标优化可行性验证

1) 时间可行性

由于辅助网络在决策时的耗时远小于多目标优化，故首先验证多目标优化方法的实时性，本文采用MOGWO作为求解模型的算法，随机产生100组敌我态势并使用算法寻优，仿真时灰狼种群与外部种群数均设置为30，迭代次数为3次。

采用MATLAB自带的计时功能记录了100次决策时间，决策平均时长t=0.286 541 s，远小于决策步长1 s，故决策模型具有良好的实时性。

为了展示寻优效果，图5记录了上述实验过程中的一次寻优的结果，其中红点为算法寻优结果，蓝点为可行域的大致范围(通过穷举法得出)，可以看出MOGWO可以在上述条件下找到基本完整、均匀的Pareto边界。

2) 决策可行性

验证通过多目标优化方法决策集的可行性，仿真时随机产生100组初始态势，敌机按初始态势做匀速直线运动，我机在不使用辅助网络的情况下进行机动，即决策时从多目标优化的决策集中按等概率随机选取最终决策，每组仿真模拟75 s的空战情形(若在75 s内达到结束条件则提前结束仿真)。

图6记录了100组仿真中我方优化目标函数在每秒的平均值(提前结束的组自结束起至75 s的目标函数值均按结束时的目标函数值记录)。

图5 算法寻优效果Fig.5 Algorithm optimization result

通过图6可知，我机态势在多目标优化方法的决策下明显优于初始时刻，且过程中威胁参数基本始终保持递增，而能量参数仅出现一次大幅下降后同样保持递增(初始的大幅机动必然会导致能量损失)。

为了更直观地展示多目标优化的性能，图7记录了在相同初始条件下进行2次重复实验的结果(其中红色为我方轨迹，蓝色为敌方轨迹)，在初始条件相同的2次仿真中，我方做出了2次不同但均有效的机动。

图6 目标函数变化趋势Fig.6 Change trend of objective function

图7 仿真轨迹(相同初始条件)Fig.7 Simulation trajectory map (the same initial conditions)

2.2 辅助决策模型有效性验证

为了验证辅助决策模型的有效性，按照1.3节中的强化学习模型训练辅助决策网络，训练总次数为20 000次，训练中双方战机采用相同的决策模型。

为了实时反映训练效果，每进行200次训练就对辅助模型性能进行一次检测；检测方法类似2.1节中验证决策可行性的实验方法，但我机在决策时采用辅助网络(即使用1.4节决策模型)，为了节省时间，每次检测重复200次且仅记录最终结果，测试结果如图8所示。

由测试结果可以看出，随着训练次数的增加，我方的获胜次数明显得到了提升，获胜概率从25%左右提升到50%左右，说明在辅助网络的帮助下，模型可以给出更为有效的决策。此外，由于双方初始位置为随机产生，每次测试中必然会出现少数极端不利的初始条件，故测试结果中一直存在一定的失败次数。

为了进一步体现辅助网络的效果，使用带辅助网络的决策模型与仅使用多目标优化方法的决策模型进行对抗仿真(将仅使用优化方法的一方视为敌机)，为了使仿真结果更具代表性，初始态势将在一定范围内随机产生，具体约束条件如下。

1) 初始有利(αe+αu∈[0°,90°])。

2) 初始均势(αe+αu∈(90°,270°))。

3) 初始不利(αe+αu∈[270°,360°])。

在3种情形下各进行100次对抗仿真，结果如表1所示。

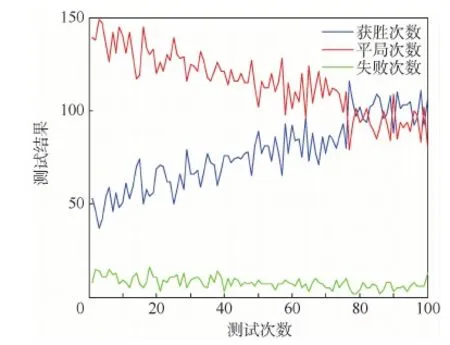
图8 辅助决策模型性能测试结果Fig.8 Test results of auxiliary decision model’s performance

初始条件获 胜平 局失 败初始有利59410初始均势325117初始不利113950

通过仿真结果可知，在使用了辅助网络后，决策模型可以做出更高效、更具有对抗性的决策，平均获胜概率提升了11.7%。

2.3 机动决策模型性能仿真

为了体现本文机动决策模型的性能，设置了2种情形下的空战环境，其中敌机采用的机动均为经典的战术动作，我机采用基于多目标优化的机动决策模型，辅助决策网络采用2.2节仿真实验中训练出来的神经网络。

1) 情形1中，我机初始处于较优的态势环境，敌机采用“S型”机动进行规避，仿真结果如图9所示。图中红色为我方，蓝色为敌方，轨迹上的飞机模型表示飞机当前姿态，相邻2个模型时间间隔为4 s。

图10分别给出了空战过程中双方攻击判定条件(视线角与距离，我机视线角αu的定义见图2，敌机视线角即为π-αe)以及我方决策得出的控制量的实时变化情况。

通过仿真数据可知，初始条件下我方占据较大优势，决策模型根据敌方位置调整我方视线角以形成攻击条件；但由于我方速度较大且敌方采取“S型”机动，在20 s左右我方基本完成转向后存在超越敌方的风险；决策模型采用了类似异面机动的原理，先适当俯冲再拉起机头以避免战机冲前，在拉起机头的过程中再次调整视线角；从第44 s开始对敌方形成有效攻击条件并保持，47 s时达到仿真结束条件，我方获胜。

情形2中，我方初始处于不利条件，但由于距离敌机较远，故存在机动规避的空间；敌机采用“纯跟踪”的方法试图接近并攻击我方，仿真结果如图11所示(图中标记同情形1)。

图9 仿真轨迹(初始有利)Fig.9 Simulation trajectory map (favorable initial conditions)

图10 态势关系与控制量(初始有利)Fig.10 Situation relationship and control quantity (favorable initial conditions)

图12分别给出了空战过程中双方攻击判定条件(视线角与距离)以及我方决策得出的控制量的实时变化情况。

通过仿真数据可知，初始我方处于不利态势，决策模型选择在向右机动规避的同时拉起机头；爬升的过程必然会损失动能，故双方距离逐渐缩小，15s左右时，敌方开始右转以保持态势优势；由于此时我方速度较低，具有更小的转弯半径，决策模型选择向右下方急转接敌，并在第29 s抢先形成攻击条件并保持，32 s时达到仿真结束条件，我方获胜。

图11 仿真轨迹(初始不利)Fig.11 Simulation trajectory map (adverse initial conditions)

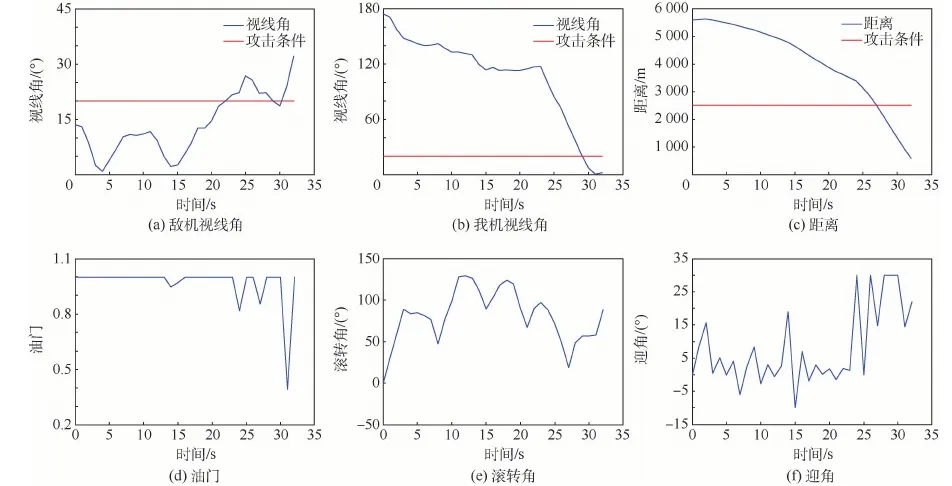
图12 态势关系与控制量(初始不利)Fig.12 Situation relationship and control quantity (adverse initial conditions)

3 结 论

本文提出了多目标优化与强化学习相结合的机动决策模型，模型融合了传统优化方法与机器学习方法的优点：

1) 多目标优化方法解决了传统优化方法中处理目标函数权重的问题，增加了决策模型的可信度和可拓展性。

2) 多目标优化方法继承了传统优化方法的优点，可以进行实时有效的机动决策。

3) 多目标优化的决策集直接给出了足够的可执行决策，极大程度上简化了动作空间，使强化学习任务具备了可行性。

4) 通过强化学习建立辅助决策网络，从而可以在多目标优化决策集中做出更好的选择，弥补了优化方法在对抗、博弈问题上的不足。

由于本文重点在于结合传统优化方法和机器学习方法，在设置优化目标时仅针对较为理想的仿真环境设置了2个目标，设置在复杂电磁环境下新的目标函数模型是下一步的改进方向。