双馈风力发电机低电压穿越控制策略量化评价
邓三星, 张雪敏, 刘 辉, 陈来军
(1. 清华大学电机工程与应用电子技术系, 北京市 100084; 2. 国网冀北电力有限公司电力科学研究院, 北京市 100045)
0 引言
风电作为一类重要的新能源发电形式,逐渐在电力系统中占据重要地位[1-2]。为提升风电接入的友好性,除了风电稳态运行控制外,更需要关注暂态过程中的风电运行控制和分析。双馈风力发电机(DFIG)的低电压穿越(LVRT)能力是衡量其暂态运行能力的关键指标,GB/T 19963—2011对于并网DFIG的LVRT要求主要包括两方面,即连续运行不脱网和动态无功支撑。
DFIG在电网电压大幅跌落时,可能出现转子过流以及直流母线过压等严重威胁换流器安全运行的暂态现象。基于对故障期间DFIG动态行为的分析,结合国标对其暂态运行能力的要求,许多学者对提高DFIG的LVRT能力进行了研究[3-6]。这些研究主要可分为保护类和控制类两种策略,保护类策略一般指加装物理保护电路对多余的暂态能量进行处理,而控制类策略则多通过改进故障控制策略,以改善故障期间DFIG的暂态性能,满足LVRT要求。工程上最常见的保护类策略是加装Crowbar保护电路吸收故障期间的暂态能量[4]。控制类策略则主要分为基于比例—积分(PI)的附加控制以及非线性控制。
基于PI的附加控制通过在常规PI控制的基础上增加前馈[3]以及“去磁”[6]等环节,能够降低暂态初期的转子电流,提升LVRT能力,但是故障期间的动态响应不足,换流器控制能力也没有得到充分利用。非线性控制结合DFIG模型的非线性特点,动态响应得到提升,但是由于所采用的三阶DFIG模型忽略了定子磁链的动态,故障初期的转子过流等现象没有得到有效改善[5]。可见,上述策略虽然具备一定的LVRT能力,但仍存在较大的改进空间。而现有研究对各控制策略LVRT效果的验证多为基于仿真的定性分析,系统的动态过程不易量化,且缺乏理论依据,无法定量地对控制策略进行评价。
综上,考虑DFIG系统的动态过程,提出定量的评价标准,既能从物理本质上分析各个控制策略的优劣,又能从控制效果上对控制策略的改进进行指导。由于LVRT标准规定故障持续一段时间内DFIG不脱网运行,因此需要分析DFIG控制系统在持续故障下的动态响应。输入—状态稳定(input-to-state stability,ISS)理论能够直观地反映系统的动态过程,并且量化外界扰动对系统的影响,适用于研究持续故障下DFIG控制系统的动态过程。文献[7]分析了同步发电机和异步电动机的输入—输出稳定(input-to-output stability,IOS)属性,其求解持续干扰下系统响应的方法值得借鉴。
本文利用局部IOS理论对外部电压干扰下DFIG的LVRT控制策略进行定量分析和评价。结合DFIG实际运行要求,量化了各个控制策略的扰动承受能力和输入—输出增益,并给出了有效的改进方案。
1 DFIG故障控制策略
DFIG常规PI解耦控制是针对稳态运行点设计的,其在遭受暂态干扰时,系统运行点发生较大偏移,PI控制不能够保证良好的暂态控制性能。因此,DFIG在故障期间的控制策略引起了广泛关注,原理上可以分为基于PI的附加控制以及非线性控制等。基于PI的附加控制,即控制的基础依然是基于矢量定向的PI控制,同时考虑了DFIG故障期间的动态特性而进行的改进控制。这一类控制主要包括“去磁”控制[6]以及前馈控制[3]等。非线性控制则充分考虑了DFIG模型的非线性特征,在故障期间采用非线性控制代替PI控制,这一类控制包括滑模控制[8]、神经网络控制[9]、状态相关黎卡提方程(SDRE)控制[5]等。
可以看到,这些控制策略的设计原理不同,因而故障期间表现出的效果存在差异。本文旨在通过一种定量评价方案来分析这些控制策略的差异,进而为各个控制方案的优化改进提供理论基础。本文选取4种方案进行测试,分别为PI控制[10]、基于PI的“去磁”控制[6]和改进前馈控制[3]以及SDRE控制[5],各个方案的设计细节可以在相应的文献里找到。需要注意的是,文献[3]的前馈控制结论是基于定子磁链d轴定向进行推导的,本文用到的改进前馈控制设计策略为基于定子电压d轴定向推导的结论,具体推导流程见附录A。
2 LISS/LIOS基本理论
ISS理论在1989年提出[11],现已广泛应用于航天器控制[12]、计算机网络拥塞控制[13]等领域。将ISS定义的状态变量换成输出量,即是IOS理论。与常规的电力系统Lyapunov稳定分析方法相比,ISS/IOS理论能够分析含有外界扰动的系统的稳定性,并且量化系统所能承受的外界扰动的大小。实际工程系统绝大多数具有运行约束,因此相对于全局稳定性分析,局部稳定性分析的结果更有工程意义,相应地,局部ISS/IOS表示为LISS/LIOS(local ISS/IOS)。
接下来简要给出LIOS的两种定义,为DFIG故障控制策略评价奠定理论基础。两类函数KL和K∞的定义以及LISS/LIOS理论定义的详细内容可见附录B,本节只做简要介绍。
考虑具有输出量的系统为:

(1)
式中:状态变量x∈D∈Rn;输入u∈U∈Rp;输出y∈Y∈Rm;f(·):Rn+p→Rn,h(·):Rn+p→Rm,都为连续Lipschitz函数且有f(0,0)=0,h(0,0)=0。
定义1:对于任意状态变量初值x0∈Ω∈Rn,输入u∈U∈Rp,输出y∈Y∈Rm,如果存在β∈KL,γ∈K∞,则
|y(t,x0,u)|≤β(|x0|,t)+γ(‖u‖∞) ∀t≥0
(2)
则式(1)表示的系统是LIOS的,其中γ称为输入—输出渐近增益,初值和输入的范围称为局部输入—输出稳定域W,W={THX〗x0,u〗|x0∈Ω,u∈U}。
需要注意的是,实际工程具有稳定运行的平衡点,因此本文对于式(1)和式(2)的状态变量、输入量和输出量的讨论都是指相对于平衡点的偏移量。
非线性鲁棒控制采用L2增益定量刻画输入对输出的影响,该值具有明确的工程意义,即L2增益越小,表明干扰对于系统的影响越小,系统的鲁棒性越强[14]。与L2增益类似,LIOS理论利用无穷范数衡量系统的输入,式(2)中的渐近增益γ反映了输入对于输出量的影响,即能够直接反映系统对于干扰的响应能力。
从式(2)可以看到,利用无穷范数衡量输入信号,仅能反映输入扰动的幅值信息,其在时间尺度上的波动信息则不能很好地体现。
定义2:考虑系统1,对于任意状态变量初值x0∈D∈Rn,输入u∈U∈Rp以及输出y∈Y∈Rm,系统满足:

(3)
则称系统(1)满足局部输出积分—积分估计,其中,增益函数α,α0,γ∈K∞。
文献[15]指出,一个系统是ISS的,当且仅当它满足积分—积分估计,因此满足式(3)的系统即是LIOS的。而式(3)与输入量和输出量的积分有关,二者分别代表了输入量以及输出量能量的大小。考虑到实际工程关心的是系统在受到干扰下能否回到稳定运行的平衡点,因此以平衡点为计算积分的参考点具有实际意义,据此定义积分能量表达式为:

(4)
其中,符号~表示变量的偏移,ue和ye分别为输入量和输出量的稳态运行平衡点,式(1)至式(4)里面的最大输入为‖u‖∞;增益函数γ,α,α0以及动态函数β称为LIOS的稳定属性。与范数形式下的最大输入‖u‖∞对应,积分—积分估计形式下,也存在一个最大输入积分能量。
3 DFIG稳定属性求取思路
实际系统难以精确建模,因此纯解析求解LIOS属性的方法[16-17]很难应用于较复杂的系统。DFIG与异步发电机的最大不同在于引入了换流器进行灵活控制,因此相比异步发电机,DFIG的电力电子特性更为明显,建模更为复杂。此外,由于电力电子元件的实际运行约束以及换流器换流需要,诸多控制环节含有限幅模块,因此建立精确的数学模型难度很大。为避免实际建模的复杂性,本文借鉴文献[7]提到的仿真方法估计DFIG的LIOS属性。仿真方法需要考虑选择输入信号、输出信号以及稳定判定条件,接下来分别详细介绍。
3.1 输入信号的选择
求取DFIG的LIOS属性,首先需要确定DFIG的外部输入干扰,包括干扰的类型、波形以及持续时间。DFIG定子直接与电网相连,因此电网故障引起的电压跌落将会直接影响DFIG的内部动态响应。同时,DFIG运行受到风速影响,可能会出现运行点的不同。因此,电网故障以及风速变化是DFIG两类主要的外部扰动。电网故障时的电压跌落属于电气扰动,而风速变化属于物理扰动,除突然的阵风外风速变化较为平稳,因此两类外部干扰时间尺度显著不同。本文选取电气扰动作为主要外部扰动,即认为在电网故障发生的短时间内风速保持恒定,此时输入信号u为单输入信号u。
电网故障时,频率和电压都会发生变化。GB/T 15945—2008指出,电力系统在正常运行条件下的频率偏差限值为±0.2 Hz,系统容量较小时,偏差限值可以放宽到±0.5 Hz。DFIG能够通过快速调节交流励磁电流实现恒定频率输出,电网频率偏差在0~±0.5 Hz之内DFIG能够正常运行[18],可见在电网频率偏差范围内,DFIG风场可以正常运行,即可认为故障期间电网频率变化对于DFIG运行的影响不大。因此,本文主要考虑故障下电网电压的变化作为DFIG的干扰。文献[19]证明,外部干扰信号的输入范围可以由保持系统稳定的输入信号u(t)的(本质)上确界‖u‖∞决定。自然地,若采用阶跃信号作为外部干扰信号,通过确定‖u‖∞,可以保证任意小于‖u‖∞的其他输入信号作用于系统时,该系统仍然是稳定的。因此,本文考虑将故障时电网电压幅值的阶跃跌落作为输入干扰。
此外,考虑到故障发生时刻,电网配置的一些电力电子装置可能动作产生谐波,而电网实际运行存在谐波含量的限制,因此考虑注入一定量的谐波作为干扰信号,并按照GB/T 14549—1993的谐波标准来执行。
GB/T 19963—2011规定,在电网电压持续跌落0.8(标幺值)时,DFIG应当持续运行0.625 s不脱网,因此可以认为DFIG在这段故障时间内已经基本进入另一个新的稳定状态,所以本文考虑输入干扰的持续时间为0.625 s。
3.2 输出信号的选择
ISO分析是建立在ISS分析基础之上的。文献[20]指出,若系统是ISO的,并具备无界可观性,则系统是ISS的。因此,仿真方法求取系统输入—输出属性的前提是系统状态是稳定且可观测的,既要保证状态变量不越限,又要保证输出量在运行范围之内。一般地,状态变量作为内部量是可量测的,但是工程上并不直接输出,而是根据实际运行要求输出相应物理量,以方便进行控制和保护设置。因此,本文所选择的输出量应该是能够反映系统内部动态的可量测输出的物理量。
电网电压大幅跌落时,DFIG在故障初期可能出现转子过流的情形。究其原因,电网电压跌落时,定子磁链不能突变,DFIG定子绕组磁链将出现直流暂态量,从而在转子绕组感应出一个反电动势,若反电动势超过转子侧换流器的最大输出电压很多的情况下,会出现很大的转子电流[21]。可见,DFIG的转子电流是外部干扰与内部控制器相互作用的结果,能够体现DFIG的内部动态,因此,本文选择转子电流作为输出信号。
3.3 稳定判定条件
理论上讲,一个系统的稳定与否应该通过状态变量的观测进行分析,但是与异步发电机相比,DFIG的电力电子特性明显,因此与异步发电机的动稳定和热稳定约束相比,DFIG的主要暂态稳定约束是电力电子元件的暂态承受能力。故障瞬间的过电流将会极大地影响DFIG的稳定运行,工程上Crowbar保护的触发条件是转子电流超过2(标幺值)[4]。因此,本文对DFIG的不同LVRT控制策略分析时,皆不考虑保护的影响,即认为保护不动作,将稳定判定条件设定为:故障发生时,一旦转子电流超过2,则系统视为进入不稳定状态。
4 DFIG稳定属性估计方法
LIOS基本理论有无穷范数以及积分—积分估计两种描述形式,相比前者,后者对不同输入的适应性更好[7]。此外,考虑到DFIG控制系统复杂且存在大量的限幅环节,本文采用积分—积分估计形式进行稳定属性分析。积分—积分估计形式的稳定属性包括最大输入积分能量以及增益函数γ。由于本文通过判断转子电流是否越限作为稳定判定条件,且主要输入信号为固定持续时间的阶跃信号,因此积分—积分估计形式下的最大输入积分能量可直接由范数形式下的最大输入‖u‖∞经过积分近似得到。根据前述的输入和输出信号,不难理解,最大输入‖u‖∞即为考虑实际运行约束的最大干扰输入,输入—输出增益γ量化了持续干扰下转子电流的响应能力。接下来着重介绍对‖u‖∞和γ进行估计的具体流程。
4.1 确定最大输入

风速保持一定,DFIG在额定电压下正常运行,稳态采用PI矢量控制,故障期间采用不同的故障控制策略。以含电网规定量谐波的定子电压阶跃跌落作为输入信号,转子电流作为输出。需要注意的是,定子电压阶跃跌落仅限于幅值,即输入信号依然是正弦旋转的。不断更新干扰信号的大小,直到观察到转子电流超过2,认为DFIG失稳,记录此时输入信号u,作为最大输入‖u‖∞。对‖u‖∞积分可以得到积分—积分估计形式下的最大输入能量。
4.2 初步估计输入—输出增益


(5)
不断调整输入信号u的大小,取输出的稳态值y,根据式(4)计算得到一系列的输入—输出积分能量。考虑到K∞函数的性质,拟合满足条件式(5)的线性函数作为DFIG的输入—输出增益函数γ。
4.3 输入—输出增益的改进
由式(5)可以看到,输入—输出增益函数γ需要由输入—输出积分能量求取,即需要将γ从式(3)的积分号中分离出来,所以4.2节采用线性形式估计γ,文献[7]亦采用该方法进行了同步发电机和异步电动机的稳定属性估计。然而DFIG系统模型复杂并具有强非线性,且利用仿真方法得到的数据有毛刺,若增益函数γ仅采用线性形式,会产生较大的保守性。因此,本文采用分段线性增益形式拟合γ函数,以降低LIOS分析的保守性。接下来证明利用仿真数据,采用分段线性函数拟合γ函数的合理性,并说明计算步骤。
由4.2节得到一系列输入—输出积分能量,为了计算方便,引入新的变量v和w,对应坐标系为二维平面坐标系V×W:
(6)
在V×W坐标系内绘制积分能量图,根据积分能量点分布趋势判断分段线性函数的段数,相应的分段线性函数为:

(7)
式中:n为分段线性函数的段数;l1,l2,…,ln和a1,a2,…,an及d1,d2,…,dn为线性函数描述系数。
将该函数投影至原始坐标系,表示为:

(8)
式中:k1,k2,…,kn和c2,c3,…,cn及t1,t2,…,tn为线性函数描述系数。
仿真计算得到V×W坐标系下的各个数据点,这些数据点里包含式(7)式中各段函数之间的连接点(a1,b1),(a2,b2),…,(an-1,bn-1)。为保证γ采用分段线性函数时能够从积分号中分离出来,须首先证明由V×W坐标系下的数据点求取未进行积分转换的原始坐标系下增益γ的合理性,即说明式(7)和式(8)各个系数之间的数学关系。
证明。
首先,


k2v+0.625c2≥w
(9)
因此在V×W坐标系下,上面不等式左侧表达式相应函数w=k2v+0.625c2经过(0,0.625c2)点,结合连接点(a1,b1),并与式(7)对比得:
(10)
由斜率定义易得:
将该式代入式(9),得到:

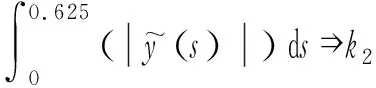
(11)
结合式(9)至式(12)得到结论。综上,下面详细介绍分段线性函数式(7)和式(8)的拟合步骤。
步骤1:利用4.3节提出的拟合方法拟合第1段线性函数w=l1v,0≤v≤a1。
步骤2:步骤1的函数得到连接点a1,b1,求得第2段线性函数w=l2v+d2,a1≤v≤a2。
其系数为:
(12)
步骤3:利用步骤2的函数得到连接点(a2,b2),求得第3段线性函数w=l3v+d3,a2≤v≤a3。
其系数为:
(13)
步骤4:依照步骤2和步骤3同样的方法求取剩余n-3段线性函数的表达式。为降低保守性,k1,k2,…,kn取满足条件的最小值。
5 算例测试
5.1 仿真算例
本文利用MATLAB/Simulink软件进行仿真分析,仿真系统如图1所示。

图1 仿真算例结构Fig.1 Structure of simulation example
9 MW的DFIG聚合模型经过集电线路接入电网,正常运行采用电压定向矢量控制。DFIG参数见附录C。通过可控交流电源模拟120 kV电网,在t=0时改变可控电源电压模拟扰动,并加入一定量的谐波。根据仿真算例电压等级,电网谐波按照GB/T 14549—1993规定的35 kV,250 MVA对应2次谐波标准来执行,通过在仿真中并联一个15 kVA,25 kV,100 Hz的电压源模拟。
根据第3,4节提出的LIOS稳定属性估计方法,对PI控制,基于PI的“去磁”控制和改进前馈控制,以及非线性SDRE控制这4种控制策略分别进行测试。需要注意的是,为了利用转子换流器的无功输出能力,PI控制器设计过程的无功功率控制部分增加了一个电压控制的环节,并设定转子电流稳态输出限幅为1(标幺值)[10]。
5.2 控制策略评价
仿真测试的最大输入‖u‖∞以及相应的积分—积分估计形式下的最大输入能量如表1所示。以PI控制为基准,“去磁”、改进前馈、非线性控制策略的积分—积分估计形式下的最大输入能量提升比例分别为2.9%,10.4%,-7.6%。可以看出,基于PI的“去磁”和改进前馈控制都能够提高DFIG能承受的最大输入,且后者能够提升约10.4%。本算例下的输入即为电压跌落深度,这意味着电网发生故障时,基于PI的“去磁”和改进前馈控制都能降低转子的过电流现象,加快转子电流的衰减,降低了DFIG脱网的风险,从而能够更好地满足DFIG的LVRT要求。非线性SDRE控制则降低了约7.6%的最大输入,表明这种控制策略加重了转子的过电流现象。究其原因,是基于PI的改进控制充分考虑了故障初期的磁链动态,而非线性SDRE控制采用的DFIG模型忽略了定子磁链的动态。

表1 各控制策略的最大输入Table 1 Maximum input of different control strategies


(14)

(15)

(16)

(17)
值得一提的是,L2增益反映干扰对于系统的影响,因此越小越好;而本文选择转子电流作为输出,输入—输出增益γ反映的是DFIG内部控制对于外部干扰的响应,从算例结论来看,γ在稳定范围内越大越好。
将4种控制的γ拟合函数结果对比放在图2。显然,在较大电压干扰下,与PI及其附加控制策略相比,DFIG在非线性SDRE控制下的转子电流积分能量更大,转子换流器输出能力强,对外反映出更强的无功输出能力,进而能够提升电压、有功功率的动态响应,而PI及其附加控制策略的转子电流积分能量相差不多,表明转子换流器输出能力较弱,对外反映出较弱的无功输出能力。定量而言,考虑电压输入可通过积分能量除以积分时间近似得到。若以竖虚线Ⅰ为分界线(此时电压输入约为0.038 8(标幺值)),认为Ⅰ左侧为小干扰,右侧为大干扰。选取竖虚线Ⅱ为大干扰典型工况(此时电压输入约为0.48),通过式(14)至式(17)计算转子电流输出能量,则SDRE控制下的输出能量是PI及其附加控制下输出能量的4.7倍。
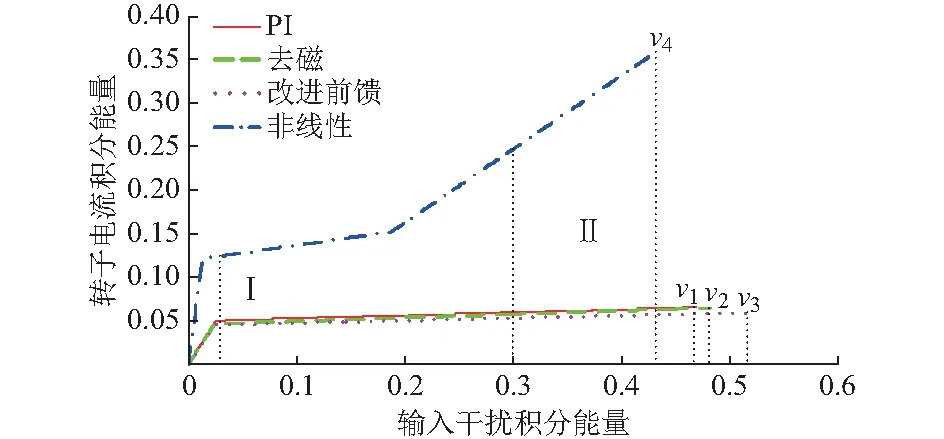
图2 各控制策略γ拟合对比Fig.2 Fitting comparison of γ with different control strategies
此外,与表1对应,图2的v1,v2,v3,v4这4个点分别表示了4种控制策略能承受的最大输入下的输入和输出积分能量。
可见,本文所提分段线性化增益函数能够较好地定量估计输入—输出增益γ,根据表2和图2定量估计的最大输入以及输入—输出增益γ的结果,本文测试的几种LVRT控制策略对比结果总结如下。
1)PI及其附加控制策略充分考虑了故障初期的动态,能够降低转子过电流,因此能够承受更大的干扰输入,抗干扰能力增加,本算例下最大能提升10.4%。小干扰下可以快速调节输出,但较大干扰时转子换流器输出能力较弱,故障后期的无功支撑作用较小。
2)非线性SDRE控制充分考虑了故障后期DFIG的非线性特征,严重故障下转子换流器输出能力强,例如本算例下,在电压输入约为0.48时,其输出能力是PI及其附加控制的4.7倍。故障后期的无功输出能力强,电压、有功功率的动态响应得到提升,但是故障初期的动态性能较差,过电流现象加重,承受干扰的能力降低,本算例下降低了7.6%。此外,非线性SDRE控制在小干扰下出现一定程度的振荡,其动态响应仍具有提升的空间。
5.3 控制策略改进
通过对以上多种控制策略的优劣进行定量评估,可以将几种控制策略相结合以改进控制性能。在本算例中,结合表1和图2定量估计的结果,通过检测干扰大小,可以设计以下两种改进的控制方案。
1)若电压干扰大于0.83(标幺值),则可采用非线性控制,并在故障初期配合Crowbar保护,既能降低故障初期的转子过电流,又能提升故障后期的无功支撑能力,从而实现整个故障期间动态响应性能的提升。
2)若电压干扰小于0.83,大于0.695,可在故障初期采用PI及其附加控制,之后采用非线性控制;前者可以降低故障初期的转子电流,后者能够提升故障后期的无功支撑能力。同时,不需要保护电路。
其中,第1种改进方案文献[5]已经进行了验证,本文着重对第2种控制改进方案进行算例测试。
仿真环境同5.1节,电压跌落深度为0.72(标幺值),故障持续0.15 s。由表1可以看到,电压跌落深度小于0.83,大于0.695,所以此电压跌落深度下,改进前馈控制可以不脱网运行,而非线性SDRE控制则会脱网,同时由图2可知改进前馈稳态输出能量小。因此,综合改进前馈控制以及非线性SDRE控制,即故障时DFIG运行采用改进前馈控制,故障持续0.05 s后切换为非线性SDRE控制,SDRE控制电流限幅取1.6(标幺值)。选取转子电流和DFIG出口电压为典型电气量[5],综合控制、改进前馈控制和非线性SDRE控制下的仿真波形见图3。

图3 DFIG的转子电流和端电压Fig.3 Rotor current and terminal voltage of DFIG
由图3(a)可知,本算例非线性SDRE控制下的最大转子电流为2.27(标幺值),而综合控制下约为1.58,转子电流显著降低且保持在最大限值内。同时,对图3(a)进行积分计算可得,本算例综合控制下,转子电流输出能量约为改进前馈控制下的3.04倍。
综上,由图3可知,基于定量分析的结论,将改进前馈控制以及非线性SDRE控制结合的控制策略既能降低故障初期的转子过电流,又能提升故障后期的电压支撑能力,即在无附加硬件时,充分利用了两种控制策略的优势。
6 结语
基于LIOS理论,本文提出了一种DFIG不同LVRT控制策略的定量评价指标,为各个控制策略的优化改进提供了理论基础。本方法的主要特点如下。
1)采用仿真方法估计LIOS属性,避开了DFIG控制里如限幅等难以建模的环节。
2)采用LIOS积分—积分估计形式进行LIOS属性量化分析,并利用积分能量,证明了采用分段线性函数对输入—输出增益进行拟合的可行性。与线性增益相比,分段线性增益估计更准确,保守性更小。
3)仿真充分考虑了DFIG在故障下的内部动态响应,同时结合了电网实际运行的要求,包括DFIG并网LVRT标准以及谐波要求等。
对几种控制策略进行的算例测试证实了本文量化评价方案的效果。根据测试的定量结果提供了改进优化的方案,并通过算例证实了本文所提控制策略量化评价方法能够为DFIG控制策略的设计和改进提供依据。
此外,本文估计的DFIG输入—输出增益还是含DFIG互联系统稳定分析的基础。然而,由于其中涉及非线性增益不等式组求解,还须开展进一步的研究工作。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

