A Quantum Secret Sharing Scheme Using Orbital Angular Momentum onto Multiple Spin States Based on Fibonacci Compression Encoding∗
Hong Lai(赖红), Ming-Xing Luo(罗明星),Yong-Jian Xu(徐永健),Josef Pieprzyk,Jun Zhang(张军), Lei Pan(潘磊),and Mehmet A.Orgun
1School of Computer and Information Science and Centre for Research and Innovation in Software Engineering(RISE),Southwest University,Chongqing 400715,China
2Information Security and National Computing Grid Laboratory,School of Information Science and Technology,Southwest Jiaotong University,Chengdu 610031,China
3Data61,Commonwealth Scientific and Industrial Research Organisation,Sydney,Australia
4Institute of Computer Science,Polish Academy of Sciences,Warsaw,01-248,Poland
5School of Software and Electrical Engineering,Swinburne University of Technology,Hawthorn,VIC,3122,Australia
6School of Information Technology,Deakin University,Geelong,VIC,3220,Australia
7Department of Computing,Macquarie University,Sydney,NSW 2109,Australia
8Faculty of Information Technology,Macau University of Science and Technology,Avenida Wai Long,Taipa,999078,Macau
AbstractSince the use of a quantum channel is very expensive for transmitting large messages,it is vital to develop an effective quantum compression encoding scheme that is easy to implement.Given that,with the single-photon spin-orbit entanglement,we propose a quantum secret sharing scheme using orbital angular momentum onto multiple spin states based on Fibonacci compression encoding.In our proposed scheme,we can represent the frequency of any secret message which is typically collection of bits encodings of text or integers as a bitstring using the base Fibonacci sequence,which is encoded multiple spin states for secret shares transmitted to participants.We demonstrate that Fibonacci compression encoding carries excellent properties that enable us to achieve more robust quantum secret sharing schemes with fewer number of photons.
Key words:spin-orbit entanglement,multiple spin states,Fibonacci compression encoding,quantum secret sharing
1 Introduction
In 1979,Shamir[1]and Blakeley[2]showed how a secret can be shared among a group of participants.Shamir used an algebraic construction while Blakley applied a geometric approach.In their schemes,if the number of collaborating participants is above the set threshold,then they can recover the secret.Conversely,if the number of participants in any given subset is below the set threshold,then they should obtain nothing about the secret.In 1999,Hillery et al.[3]proposed a quantum secret sharing(QSS)scheme based on the Greenberger-Horne-Zeilinger(GHZ)state.[4]The Hillery et al.scheme uses entangled quantum states to share a secret in the context of classic cryptography.In the same year,Cleve et al.[5]introduced an alternative QSS scheme that allows quantum state sharing(QSTS).For these schemes based on quantum mechanics,[6]participants use certain quantum techniques to share a secret,which makes it possible to achieve unconditionally secure QSS schemes.Inspired by their schemes,more and more authors have shown great interest in the study of QSS[7−13]and QSTS.[14−16]
On the other hand,in 1909,Poynting[17]discovered that light waves have spin angular momentum(SAM).In 1992,Allen et al.[18]observed that a photon carries orbital angular momentum(OAM)as well.Using SAM photon freedom,qubit coding can be conducted in a similar manner to the demonstration provided by Bennett and Bras-sard in their quantum key distribution(QKD).[19]An interesting property of photon OAM is that it can achieve a high dimensional quantum state coding(i.e.qudit coding).In 2002,Leach et al.[20]conducted experiments with encoding separation techniques using photonic OAM.They pointed out that the OAM carrier could greatly improve the communication capacity of a single photon.In 2001,Mair et al.[21]experimentally demonstrated that photon pairs prepared by the spontaneous parametric down conversion(SPDC)share similar characteristics to those of OAM.A year later,Leach et al.[20]devised an interferometric technique that individually recognizes photons in arbitrarily many OAM states and routes each of the photons.Leach et al.advanced[22]their techniques to measure the orbital,spin or total angular momenta and subsequently a successful measurement of the sign of OAM of a light beam using a Shack Hartmann wavefront sensor.[23]In 2015,with OAM of photons,Mi et al.[24]proposed a high-capacity quantum secure direct communication.By using the rotational Doppler shift and an interferometer spanning the angle space,Vasnetsov et al.[25]and Zambrini and Barnett[26]discovered the resolution of the OAM spectrum respectively.Consequently,these developments ignited a great interest in studying quantum information processing with enlarged sets of alphabets based on OAM sorting.
A separate line of research deals with the problem of how to achieve a coupling between SAM and OAM in an inhomogeneous and anisotropic medium(which is also known as q-plates).[27]Q-plates together with quantum information transfer between different degrees of freedom were studied by Nagali et al.[28]In this context,Chen and She demonstrated the Shannon dimensionality increase.[29]In 2009,Chen and She[30]proposed to use an OAM-dependent polarization manipulation technique to design a practical scheme,which is able to sort OAM by cascading conventional polarizing beam splitters.Moreover,they found that their scheme could induce spinorbit coupling.This provides an alternative technique for encoding OAM onto multiple spin states using a Hu ffman tree.[31]The technique could have some potential use in optical communication.Although Huffman codes have the optimal compression ratio,the encoding and decoding process is complicated as it depends on the probability distribution of the alphabetical letters in the given message.Moreover,its robustness against errors is absent.In order to address these problems,we propose to use a new variable-length codewords,i.e.,a binary Fibonacci numeration system.We show how to use them to design quantum secret sharing with Fibonacci compression encoding based on the technique proposed by Chen and She.[30]
The rest of paper is organized as follows.Section 2 discusses Fibonacci sequences,Fibonacci representation and Fibonacci diagonal matrices.Section 3 describes the proposed compressed QSS scheme.The security analysis and features of the protocol are presented in Secs.4 and 5,respectively.Section 6 concludes the work.
2 Fibonacci Sequences,Fibonacci Representation and Fibonacci Diagonal Matrices
In this section,we give the necessary background on Fibonacci sequences and related mathematical structures that we use in the paper.
2.1 Fibonacci Sequences
The Fibonacci sequence for our proposed scheme is defi ned as follows:
Definition 1Fibonacci sequence Fifor(i= 0,1,2,...)[32]satisfies the following recurrence relation:
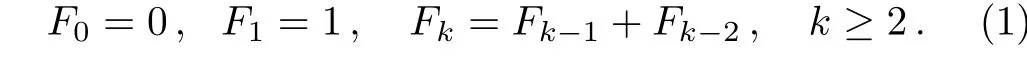
Therefore,the first few Fibonacci numbers are 0,1,1,2,3,5,8,13,21,34,55,89,...
Alternatively,the Fibonacci sequence can be represented as follows[33]
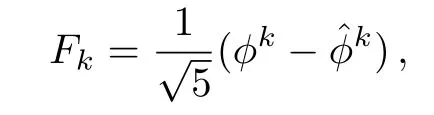
2.2 Fibonacci Representation
A fundamental theorem in discrete mathematics states that any positive integer can be represented by Fibonacci bases.[34]The following definition describes the representation.
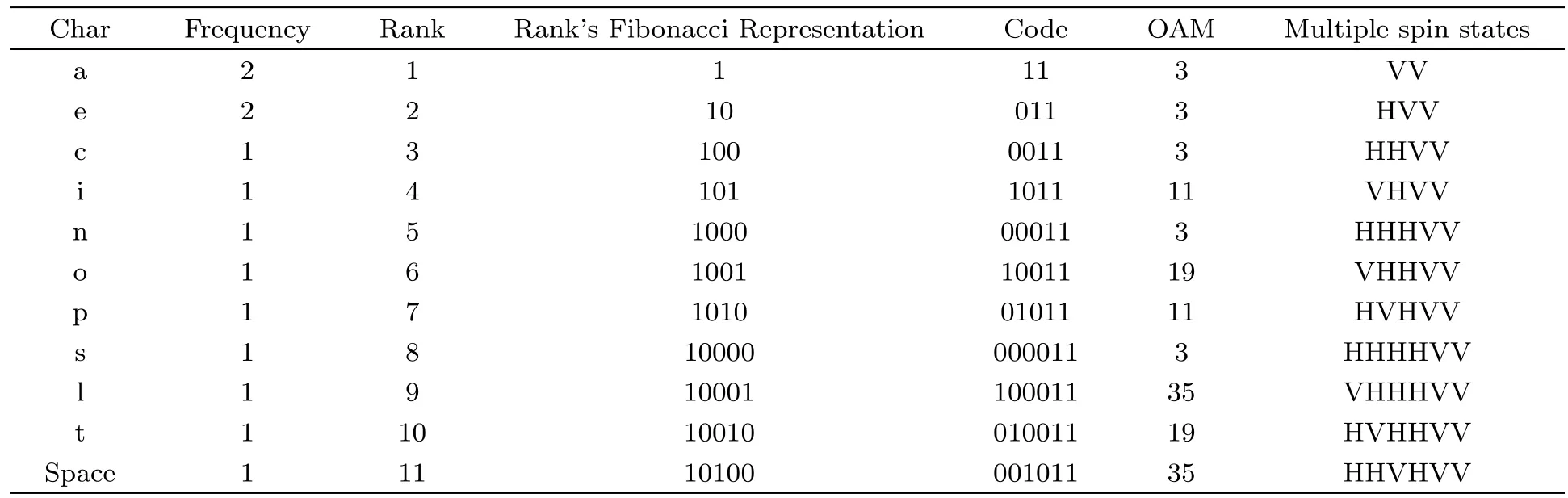
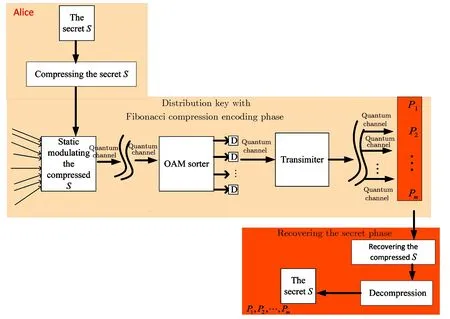
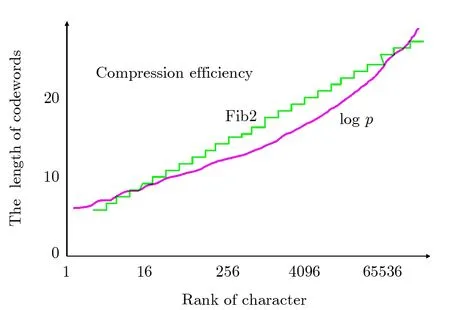
Definition 2(Fibonacci representation[34])For any positive integer n,there exists a finite subset S ={l1,l2,...,lk}of the natural numbers,where l1 (i)Fl1+Fl2+ ···+Flk=n. (ii)For all i,Fli+1≥Fli+2(no adjacent ones). There is also an efficient algorithm that produces such representation. Algorithm Parameters:Fibonacci bases Fl1,Fl2,Fl3,...,Flk.Input:an integer n. Output:a sequence S such that∑Fli=n. (i)S=∅. (ii) For i∈[1,k]be the largest number such that Fli≤n. (iii)S=li. (iv)n→n−Fli. Proposition 1[34]The Fibonacci representation of an integer is uniquely decodable. Example 1According to the above-mentioned algorithm,the integer 45 can be represented using Fibonacci sequence as follows: where S={3,5,8}. The simplest Fibonacci matrix can be constructed from the first three Fibonacci numbers 0,1,1 as follows:[35] where det(Q1)=F0F2−= −1.Using Eq.(1),we can compute the k-th power of the Fibonacci matrixas follows Fibonacci block diagonal matrices are defined as follows: So,the Fibonacci block diagonal matrix for Example 1 is where O is a matrix of dimension 2×2 with zero entries. In this section,we apply the technique based on Ref.[30]to encode OAM onto multiple spin states using Fibonacci compression encoding and propose a quantum secret sharing scheme.We note that Fibonacci compression encoding[36]enjoys excellent properties that enable us to design a compressed QSS scheme.The proposed scheme can greatly increase the transmission capacity,and thus save qubits for the transmission.Most importantly,it provides extra resilience to the attacks against the secret message. Our QSS scheme includes two phases,i.e.,distributing key with Fibonacci compression encoding phase and recovering secret phase.There are three kinds of roles involved in our compressed QSS scheme,which are as follows: (i)A Dealer. (ii)Quantum participants. (iii)An adversary. The dealer(Alice),which is at a free-space OAM qudit network,is responsible for converting a classical secret message into multiple spin states and sending them to m quantum participants P1,P2,...,Pm. Quantum participants,denoted as P1,P2,...,Pmconnected viaaqubitnetwork,hold quantum shares s1,s2,...,smrespectively.Their task is to detect eavesdropping and jointly recover the shared secret. The adversary,who could also be any of participants,can eavesdrop the transmitted information over the quantum channel. Our scheme accepts the triplet:a secret S(this is typically collection of bits,which are encodings of text or integers),a designated collection of participants P={P1,P2,...,Pm}from an access structure Γ as an input.The access structure Γ determines a collection of participants that are authorized to reconstruct the secret.It outputs quantum shares si,i=1,2,...,m-multiple spin states for participants Pi,i=1,2,...,m. The detailed steps of our protocol are given as follows:Step 1 Compressing the secretThe Dealer sets up the secret sharing.She computes the frequency of every block(for example,each sentence of a secrete text can be regarded as a block)of S and represents them in Fibonacci bases such as 34,21,13,8,5,3,2,1,(see Definition 2). The compressing processes are performed in clearly separated stages: (i)Compute the frequencies of the collection of bits which are encodings of the text or the integers. (ii)Rank the collection of bits by their frequencies. (iii)Compute the Fibonacci code of each ranking. (iv) Output the ranking as the header of the compressed secret. (v)Reread the input secret S,using the code table to generate the output and transfer it to the compressed secret. Step 2 Quantum encodingThe step aims to convert the binary codes 1s and 0s into single photon’s polarizations Vs and Hs.The Dealer encodes the frequencies with OAM by assigning a twisted number of a single photon to each Fibonacci value:.That is,only 8 different twists are required in terms of Chen and She’s work[30](see Fig.1).Moreover,the Dealer encodes every character into binary codes,i.e.,1s and 0s which are represented by single photon’s polarizations Vs and Hs.Also,to remove this encoding ambiguity,we append an extra bit 1 to every character binary codes,which is used to act as a “comma”,separating consecutive codewords. Step 3 Distributing the keyAs shown in Fig.1,Alice sends the quantum shares to P1,P2,...,Pmaccording to the setting of an array of angularly separated light sources illuminating the static phase mask.After entering static modulation,the input planar photons are converted into twisted ones with coinciding propagation direction.Each twist number assigned is selectively dependent on their inclinations in front of the phase mask. Then,the encoded twisted photons are sent into the free-space link by an afocal telescope.The Dealer’s qudit receiver consists of a similar telescope,the aforementioned OAM sorter,and an array of photodiode detectors which are set up to monitor the output intensity of each port.Thus,the aggregated information is used to decode the message.The Dealer Alice can encode the secret message as binary codes(spin),and send quantum shares–the corresponding multiple spin states through the quantum channel,and publish the determinants of Fibonacci diagonal matrices to participants P1,P2,...,Pmthrough the classical communication channel. Example 2Take the secret message“action please” as an example to illustrate Steps 1-3,we can obtain the encoded information listed in Table 1. Table 1 Compress and encode the secret message “action please” as binary bits,where each binary code(0 or 1)is represented by a single photon’s polarization(H or V). The Dealer sends VV to P1,HHVV to P2,...,HVV to P10via the quantum channel.At the same time,the Dealer publishes det(),det(),...,det()via the classical channel. In this phase,the system accepts the triplet:quantum shares s1,s2,...,smand a set of currently active participants{P1,P2,...,Pm}as the input.It outputs the aggregated secret S if{P1,P2,...,Pm}are verified,or“FAIL”otherwise. The detailed steps are as follows: Step1 EavesdroppingDetectionUpon recipient of these multiple spin states,the participants{P1,P2,...,Pm}can obtain their qubits.According to Table 1,they first verify the determinants of Fibonacci diagonal matrices consisting of the Rank’s Fibonacci bases in terms of Eq.(5).If they are different,they immediately abort the communication and the final output is FAIL.Otherwise,they continue to obtain the matching codes. Step 2 Secret RecoveryAfter confirming that the secret shares received by all participants are valid,the Dealer informs the nominated aggregator immediately(which can be any participant)on the positions of every character or integer of the collection of bits.Finally,the secret S can be reconstructed by concatenating all the decoded pieces based on each participant’s secret share.An example is provided in Table 1. In Example 2,according to the published det(),det(),...,det()by the Dealer,P1,...,P10can detect potential eavesdropping in terms of Eq.(5).If the com-puted determinants from P1,...,P10are identical to the Dealer’s published values,P1can obtain “a” from the code word VV,P2can obtain “c” from the code word HHVV,···,P10can obtain “e” from the code word HVV.At last,they can obtain the secret message “action please”. In this section,we analyze the security of the proposed QSS scheme in the presence of some known attack strategies. As shown in Fig.1,the Dealer manipulates the qudit state of the signal photons only in her private side and keeps these photons all the time.Similarly,the participants P1,P2,...,Pmmanipulate the qubit states in their own sides.In these private places,it is not possible for the adversary Eve to have access to the photons.Nevertheless,participants P1,P2,...,Pmdo not always keep the qubit photons,providing a chance for Eve’s eavesdropping.That is,Eve can intercept the qubit photons from the Dealer to the participants P1,P2,...,Pmin the free space,and then send the unoriginal qubit photons to P1,P2,...,Pm,i.e.,man-in-the-middle attacks.However,our scheme can defend the secrets against the man-in-themiddle attack.This is because we can use the determinant of matching Fibonacci diagonal matrices of photon’s information to verify the identification of every participant. Take Table 1 for example,if the adversary Eve intercepts the multiple spin states HVV from the Dealer to participant 2,and then re-sends HHVV to participant 2.However,the determinant of matching Fibonacci diagonal matrices is also changed.In this case,the Fibonacci diagonal matrix is changed to Our scheme uses an access control mechanism,i.e.only designated participants can recover the secret.So,we consider the attacks launched from the external participants here.We analyze the following three scenarios. (i)Firstly,as shown in Fig.1,the external participant who is located at the other side of the qubit network,cannot see the secret message over the qudit network directly. (ii)Secondly,according to Eq.(5),we use the determinants of Fibonacci diagonal matrices consisting of the rank’s Fibonacci bases to verify the identity of the participant.For example,if a participant receives multiple spin states HVV and its Rank’s Fibonacci base is 2,then the Fibonacci diagonal matrices is (iii)Finally,even if the external participants can obtain the quantum information,any attacks can be detected by the compression coding with representation of every block.Each sentence or a certain number of letters can be regarded as a block of the secret.The position of every letters of a block is only given to the legal participants through the secure channel.Therefore,the external participants cannot obtain the secret. The photon-number-splitting(PNS)attack is defined as follows:as non-ideal light sources are used in quantum cryptography,the number of produced photons can be multiple,providing a chance for the attacker Eve to obtain the transmitted quantum messages in two-way quantum communications.However,as shown in Fig.1,our scheme is one-way and we use orbital angular momentum onto multiple spin states rather than spin angular momentum.Therefore,Eve cannot obtain the secret using the photon-number-splitting(PNS)attack. Based on Chen and She’s work,[29]we have proposed a novel QSS scheme,i.e.compressed QSS.In our protocol,the q-plate is used as a qudit-to-qubit transverter to transform the polarization higher-dimensional photons into the two-dimensional photons,which provides the possibility to explore the features of the higher-dimensional space of OAM states to encode information.More importantly,our encoding process is much simpler than the Huffman encoding,because the latter must take every probability distribution of letters in the secret information into account.In addition,the actual decoding process is very similar to that of the Huffman coding.In our QSS scheme,one-to-one mapping between the multiple spin states and the participants P1,P2,...,Pmwould make the column of codewords in Table 1 superfluous.In the following,we introduce the features brought by the higher-dimensional space of OAM states in detail. (i)Our QSS scheme has high compression efficiency Due to the use of the variable-length Fibonacci compression encoding,the length of codeword is reduced tofromin the standard binary coding(see Table 2),where M is the maximal bytes of codewords length.The longer the secret messages,the more substantial the saving codes(photons)(see Fig.2).Figure 2 plots the codewords length as a function of the rank of the character on a logarithmic scale for Huffman and Fibonacci compression coding. Fig.2 The comparison of compression efficiency between Huffman encoding and our Fibonacci compression encoding. Also,as shown in Table 2,the Prob√ability of 1-bit guess is reduced from 1/2 to(1/2)(1− 1/)=0.276.Meanwhile,the average codeword lengths of 1-bit areandfor standard binary coding and our Fibonacci compression encoding respectively. Also,review Example 2,the size of header+51 bits is encoded into at most 51/10=6 bytes,though the header may be larger.With an ordinary representation,each letter of the original string “action please” in Example 2 requires one byte or 8 bits.Compared to the standard binary codes with our Fibonacci compression encoding,the length of character“a” is one fourth of that of standard binary codes.Moreover,if we can obtain a more accurate estimate of the probability of each letter in the secret message,the proportion of lossless compression can be significantly increased. Table 2 Performance comparison between standard binary encoding and Fibonacci encoding,where M is the maximal bytes of codewords length. (ii)Our QSS scheme is robustWhile inserting and deleting of a single bit,the Huffman coding may lose all the suffixes,since it renders the decoding to be shifted and all the true codeword boundaries to be missed.However,our Fibonacci coding is immune to such effects(see Fig.2),because of its explicit codeword ending. (iii)Our QSS scheme can save a substantial number of photons As shown in Fig.2,if the shared secret is long,with our Fibonacci compression encoding,the length of codes is reduced greatly,and in turn,in our QSS scheme,the number of the used photons is greatly reduced. (iv) The dealer and the participants P1,P2,...,Pmare in different kinds of a qubit network As is described in Sec.3,Dealer is at a free-space OAM qudit network while all participants P1,P2,...,Pmare at a qubit network.So,the participants P1,P2,...,Pmcould not see the Dealer’s secret,and the security is provided. The paper uses Fibonacci compression encoding to achieve a compressed QSS scheme based on orbital angular momentum onto multiple spin states.The proposed scheme improves the efficiency of photon usage due to the significant improvement over the standard binary coding.The proposed scheme also improves the level of security,because the probability of successfully guess√ing 1-bit information is reduced from 1/2 to(1/2)(1−1/=0.276.Because we use the Fibonacci compression coding to tolerate information loss,our proposed scheme is more robust than the traditional schemes using the Huffman coding.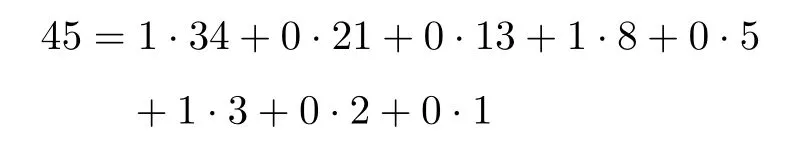
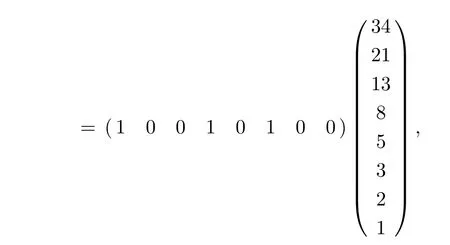
2.3 Fibonacci Block Diagonal Matrices
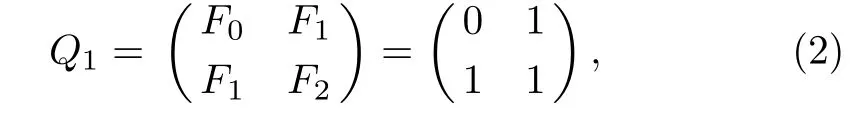
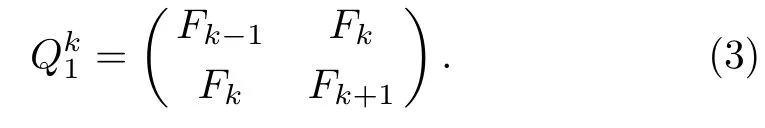
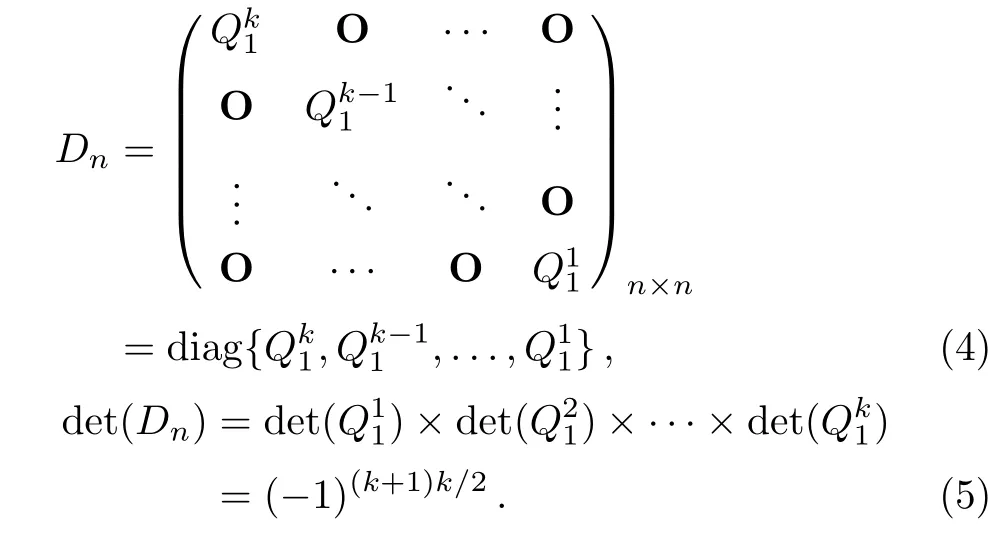
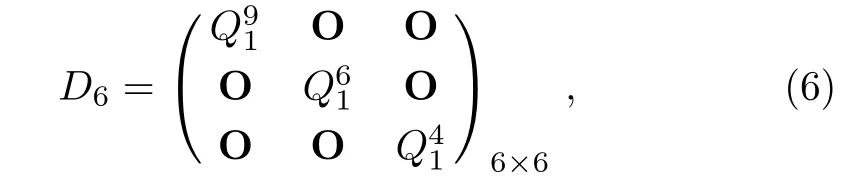
3 A QSS Scheme Based on Fibonacci Compression Encoding
3.1 Distributing Key with Fibonacci Compression Encoding Phase
3.2 Recovering the Secret Phase
4 Security Analysis
4.1 The Man-in-the-Middle Attack
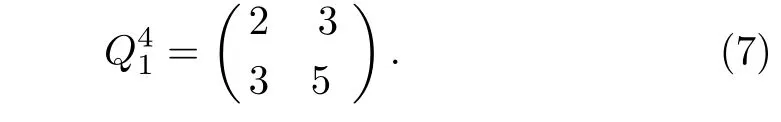
4.2 The Participants’Attack
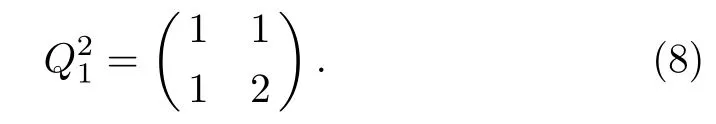
4.3 The Photon-Number-Splitting(PNS)Attack
5 Features of Our Proposed Protocol

6 Conclusion
 Communications in Theoretical Physics2018年10期
Communications in Theoretical Physics2018年10期
- Communications in Theoretical Physics的其它文章
- Topological Dark Matter from the Theory of Composite Electroweak Symmetry Breaking∗
- Analytical Investigation of Soliton Solutions to Three Quantum Zakharov-Kuznetsov Equations
- High Accuracy Split-Step Finite Difference Method for Schr¨odinger-KdV Equations∗
- Impact of Internal Heat Source on Mixed Convective Transverse Transport of Viscoplastic Material under Viscosity Variation
- Pair Production in Chromoelectric Field with Back Reaction∗
- Baryogenesis in f(R,T)Gravity∗
