基于KMV模型的贵州上市公司信贷风险评价研究

张晓耀

（贵州大学经济学院，贵阳 550025）

引言

随着我国经济社会的快速发展，金融领域发生了巨大的变化，这种变化一方面体现在量的变化上，另一方面，随着各种金融创新工具的异军突起，银行间的激烈竞争给银行带来了巨大的压力，各种违约事件的发生使得银行面临更大的风险，因此金融业迫切需要有效的风险评估方法，以用来确定企业的信用状况，并根据企业的预期违约概率，判断是否为其提供贷款。

贵州省多以中小型企业为主，企业无论是从经营规模还是经营绩效上都无法与沿海企业相比，理论上讲，贵州的商业银行面临着更大的违约风险，因此贵州急需符合自身情况的信贷管理模型，目前国内还没有专门运用KMV模型对贵州上市企业进行信贷评价的文章，本研究对于贵州商业银行信贷风险管理评价研究具有重大的理论意义与现实意义。

一、KMV模型的基本原理及计算过程

（一）KMV模型的基本原理

KMV模型由企业股票的价值、波动性、无风险利率、到期时间以及负债的账面价值，根据布莱克—斯科尔斯期权定价公式，估算出企业资产的市场价值、资产价值的波动性。然后，根据公司的长期负债与短期负债的情况来计算出企业的违约点，再根据违约点确定违约距离。最后，根据违约距离与预期违约率之间的对应关系，估计出预期违约率。

（二）KMV模型的计算过程

1．计算公司资产的价值与波动性。我们无法知道公司资产及其波动性，但是只要企业上市交易，我们就可以获取其股票的价值和股票价值的波动市场价值性，而公司股票价值和资产价值的关系，可由布莱克—斯科尔斯期权定价公式给出，表达式为公司股票价值的波动性与权益价值波动性之间的关系，可由伊藤引理推出，即其中，VE为公司权益价值；VA为公司资产价值；M为负债的账面价值；T为期权有效期；r为连续复利的无风险利率；σΕ为权益价值波动性；σA为股票价值的波动性；N（d1）、N（d2）为正态分布变量的累积概率分布函数：

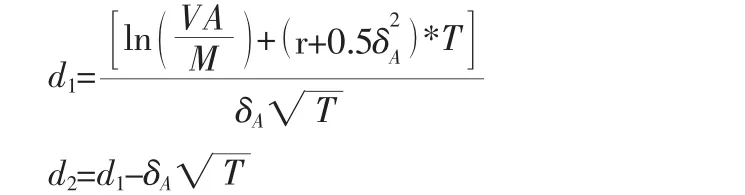
2．确定公司的违约点。违约是指合同的一方违反合同义务的行为，每家企业都是从自身的利益出发，因此如果企业资产大于负责，企业肯定不会选择违约，只有当企业没有能力支付到期债务，也即是到期债务大于资产时，企业才会考虑选择违约。但是KMV公司的研究表明，并不是当资产小于负债时企业就会选择违约，因为企业本身具有一定的缓冲能力，所以实际情况应该小于这个值。KMV公司根据对上百家违约公司的统计数据研究表明，违约点约等于短期负债加上长期负债的一半，即DPT=STD+0．5LTD，其中DPT表示违约点，STD和LTD分别为短期发展与长期负债。但我国相关学者根据我国的实际情况进行研究表明，这一违约点可能不符合我国的情况。张能福（2010）通过选取82家公司作为样本，运用Matlab软件，估算出新的违约点为DPT=1．8×STD+1．2×LTD；冯敬海等（2016）通过选取相关样本，并应用遗传算法对相关样本进行反复迭代，最后估算出最优违约点的公式为 DPT＝4．302×STD＋1．736×LTD。他们都认为，由于我国国情的特殊性，所以新的违约点更符合我国的情况。

3．确定违约距离。违约距离表示公司资产价值距离违约点的远近程度，一般用DD来表示。企业违约距离越小，表示企业资产越接近违约点，所以公司越有可能违约；相反，违约距离越大，则企业违约的概率越小，违约距离用公式可表示

二、实证过程

（一）参数的设定

1．无风险利率的确定。本文选取的是2016年中国人民银行确定的一年期定期活期存款利率作为无风险利率，即 r=1．5%。

2．股权价值的确定。股票的价值（VE）=（流通股数量+非流通股数量）×收盘价。

3．违约点DPT的确定。虽然在国内对违约点的确定存在诸多争议，但为了计算方便，本文的实证研究采用KMV公司所确定的：DPT=STD+0．5LTD。

本文的长期负债与短期负债所选取的是2016年各公司期末财务报表的相关数据，为使相关计算方便，我们假设债务的期限为一年，即T=1。

（二）样本选取

本文从中国A股和B股选取2016年10只股票，其中5只为贵州上市公司普通股票，另外5只为带有*ST标记的参照组股票。在发达国家会有专门的企业违约数据库，基于这些数据库，我们就能够判断企业经营的好坏，但由于我国还没有建立专门的历史违约数据库，相关机构一般也不对外公布企业违约情况，因此我们选取*ST公司作为易违约的企业，而在贵州上市企业中又没有*ST股票，所以我们随机从中国股票市场挑选5只股票作为参照。

（三）计算过程

1．计算股票价值波动率σE。波动率是金融资产价格上下波动的程度，是资产收益率不确定的一种表现，往往用波动率来表示项目的风险水平。有很多方法计算波动率，本文采用历史波动率法进行计算，首先要假设股票价格满足标准正态分布，因此股票的对数收益率为其中，Si为样本企业第i日的股票收盘价，Si+1为第i日后一日的收盘价。股票收益率的日波动率为，不难看出，股票的日波动率也就是样本的方差。式中，n表示的是交易天数，u¯表示的是收益率的均值，除去周末以及节假日，我国股票市场每年的交易天数大概是250天，因此股票的年波动率根据收集到的相关数据，运用matlab等数学软件，可以计算出相关结果（见表1）。

表1 股票波动率

2．计算企业资产价值（VA）、波动率（σE）与违约距离（DD）。由上面给出的布莱克—斯科尔斯期权定价理论以及伊藤引理，将计算出来的各企业的市场价值（VE）及其波动性（σE）、无风险利率（r=0．015）、期权的有效期（T=1）和负债的账面价值 M 带入公式由运用Matlab软件进行计算，即可求出企业资产价值（VA）、波动率（σE）与违约距离（DD）。所有企业的计算结果（如下页表2所示）。

3．计算预期违约概率。假如我们能够知道企业资产的概率分布，就能根据计算出的违约距离来推算出企业的违约概率，KMV公司所计算的企业违约概率是将企业以往的违约频率和违约距离相比对而得到的，但由于我国缺乏相关的违约数据库，因此国内很多学者都是采用理论上的预期违约频率来进行替代，而我们假设资产服从标准正态分布，那么根据定义，理论上的违约概率计算公式为：EDF=P（E（VA）＜DPT）=N（DPT-E（VA）．σA）=N（-DD）=1-N（DD），也就是说计算出了违约距离，我们就能够得到违约概率EDF，相关计算结果如表2最后一栏所示。

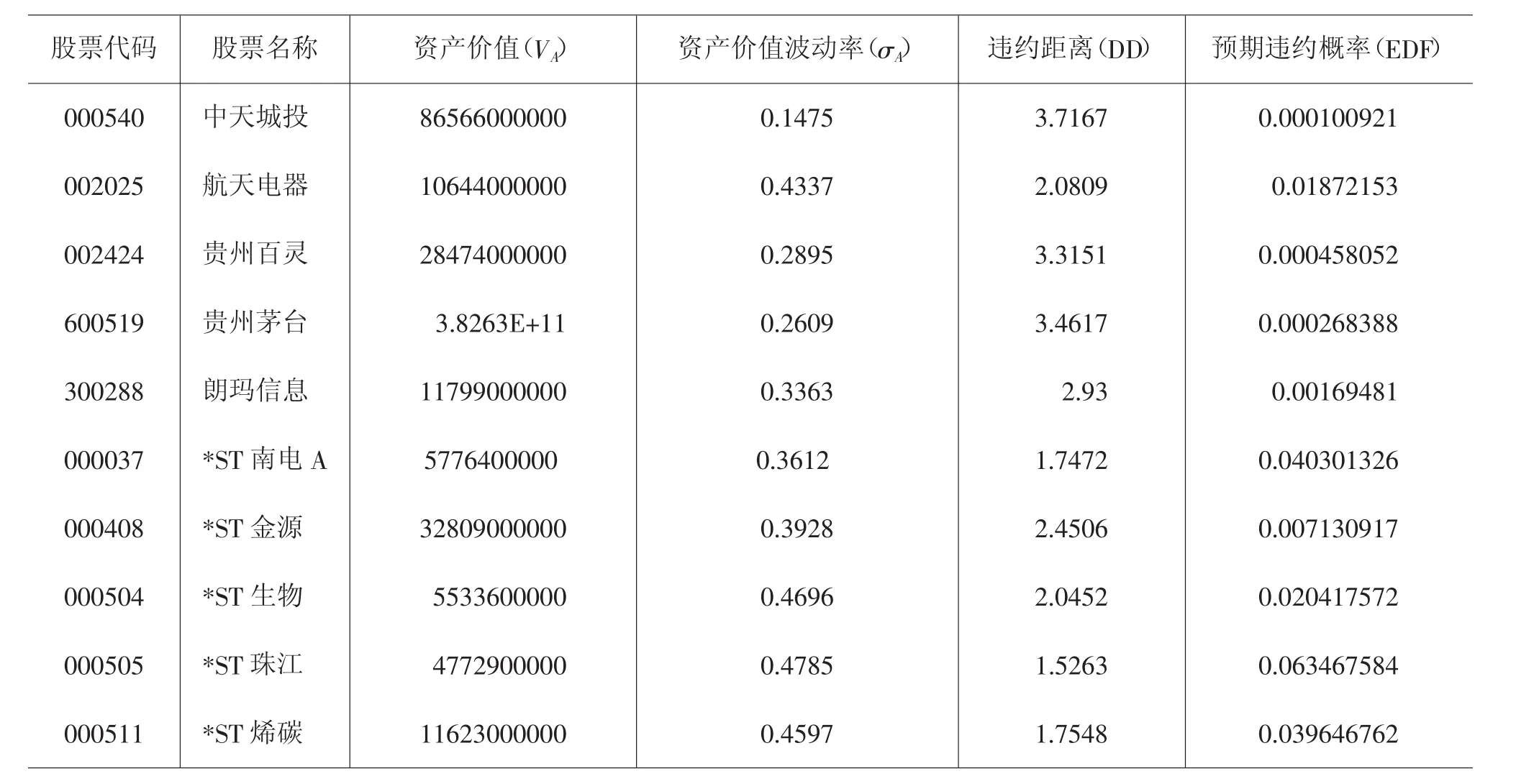
表2 企业资产价值、波动性与违约距离

三、实证结果

如表2所示，除了航天电器外，*ST公司的违约距离皆小于非*ST公司，其中违约距离最大的是中天城投（3．7167），其次是贵州茅台（3．4617），而5家*ST公司的违约距离均小于2．5，前面我们多次提到，违约距离越大，那么企业违约的可能性越小，反之亦然。从近几年的情况来看，我们得出的结论是与实际情况相符合的，因为标记为*ST的公司一般都经营不善，或者公司面临重整、和解或是破产清算等情况，因此理论上其违约距离肯定要比正常运营的企业小。而由表2可以看出，中天城投的预期违约概率最小（0．000100921），其次是贵州茅台（0．000268388），而5家被标记为*ST的上市企业预期违约概率均超过了0．007，除了航天电器的预期违约概率（0．01872153）大于 *ST 金源（0．007130917），其余的非*ST企业预期违约概率均小于*ST企业，计算结果与理论拟合度较高，说明KMV模型能够较好地反映贵州省上市企业的信用状况，企业可以运用KMV模型来判定是否为企业提供贷款，以及提供多少贷款最合适。

当然，我们也不能否认运用KMV模型对贵州上市企业进行实证时发现的一些问题，比如航天电器的违约距离小于*ST金源，而违约概率大于*ST金源，这与我们的理论假设相违背，因为根据我们的理论，所有非*ST公司的违约距离均应大于*ST公司，非*ST公司预期违约概率应该小于*ST公司，产生与理论相违背的结果可能是由以下原因引起的：第一，我国证券市场起步较晚，发展还不是很完整，存在着很多投机行为，因此股票的价格很难反映企业的真实经营情况。第二，由DD建立的理论违约概率并不能真实地反映企业的违约情况。第三，本文中假设条件过多，如假设公司的股票价值符合标准正太分布，但是有很多学者的研究表明这一假设并不成立，相反很多股票存在着“肥尾现象”，这些假设导致计算结果与实际情况不完全符合。第四，西方国家按照短期负债加长期负债的一半来计算违约点，但是由于我国证券市场起步较晚，发展还不像西方尤其是美国那样完善，因此按照他们的计算方法所确定的违约点所计算出来的结果与实际情况相异。第五，由于我国并未建立完整的企业历史违约数据库，使得我们在确定预期违约概率时，几乎不可能按照KMV公司所确立的企业历史违约数据与预期EDF的关系来确定预期违约概率。

另外，我们会发现应用KMV模型时必须要找一组数据作为参照，只有通过参考经营较差的企业的违约距离和违约概率我们才能知道所考察企业的经营状况，但是到底违约距离和预期违约概率多大代表着企业经营好坏，这里并没有一个确切的值，这也是下一步需要我们进行研究的问题。