对重上抛与回落的过程探析

张丙印

（上海现代电梯制造有限公司，上海201716）

0 引言

当电梯轿厢下行至压缩轿厢缓冲器时，对重会经历上抛与回落的过程。而回落过程中由于冲击的原因，作用在曳引轮两侧钢丝绳的张力与正常运行运动工况有较大的差别。本文主要在力学建模的基础上对对重回落过程中作用在曳引轮两侧钢丝绳的最大张力进行探析，以便为设计曳引机、承重机架等提供技术依据。

以下为解决上述问题而进行的理论建模及求解过程，旨在求出由于此过程产生的曳引轮两侧的最大张力。

1 求解钢丝绳的等效质量

将钢丝绳看做一弹簧，如图1所示，使弹簧一端固定，另一端以速度V运动，假设弹簧总质量为m，原始长度为l0，劲度系数为k，在距离固定端r处取微段dr，微段质量dm=mdr/l0，当弹簧向下产生位移x时，该质元dm相应的位移设为u，则有x/l0=u/r，即u=rx/l0。

对时间t求导，可得到质元dm的速度：

所以质元的动能dEK为：

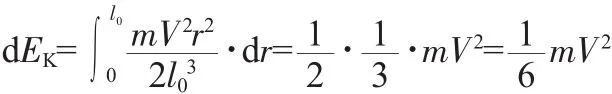
因此，该结构的等效质量为m/3。

2 轿厢压缩缓冲器后对重的运动过程分析

现以曳引比为1:1，带补偿绳张紧装置的电梯为模型进行分析。轿厢压缩缓冲器后对重的运动过程如图2所示，此过程可分为3个运动工况。

图中，P+L为轿厢自重加载重的重力；TC为随行电缆内部张力；Rh为轿厢侧主钢丝绳重力；VS为轿厢撞击缓冲器时的速度；T2为轿厢侧作用在曳引轮上的主钢丝绳内张力；T1为对重侧作用在曳引轮上的主钢丝绳内张力；W为对重自重的重力；aW为运动工况1时，对重上行减速时的减速度；Sa为运动工况1时，对重向上的减速距离；VF为运动工况1时，对重回落后，在拉直（或冲击）钢丝绳时的临界速度；V0为运动工况2时，对重回落后，在拉动轿厢运动前，此时对重的运行速度；δ为运动工况2时，对重回落后，在拉动轿厢运动前钢丝绳的延伸量；x1为运动工况3时，对重的下行移动距离；x2为运动工况3时，轿厢的上行移动距离；RC为对重侧补偿绳的重力；w为补偿绳张紧装置的重力。

图1 将钢丝绳简化为弹簧

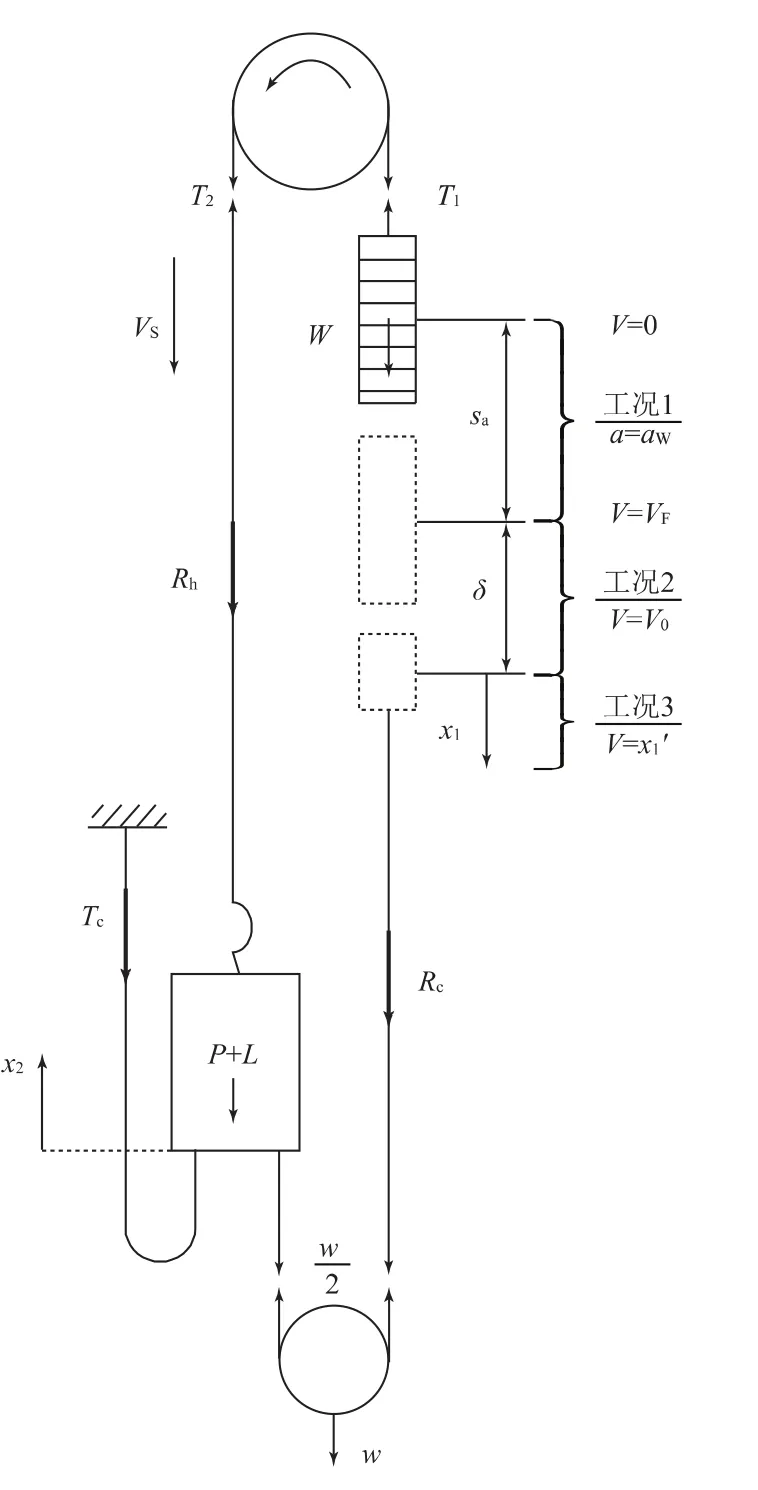
图2 轿厢压缩缓冲器后对重的运动过程

运动工况1：轿厢压缩缓冲器后对重向上减速运行，直至速度降低为0 m/s，然后对重回落至拉直（或冲击）钢丝绳时的状态。

运动工况2：对重继续下行，主钢丝绳延伸，在拉动轿厢运动前，此时对重运行速度为V0。

运动工况3：对重继续下行距离x1，拉动轿厢上行的距离为x2。

3 力学建模分析

3.1 运动工况1分析

使用整体法求解，因∑F=a∑M，所以对重侧的减速度为：

式中，a为曳引系数。

从对重减速度的表达式来看，钢丝绳越重，该减速度就越小，换言之对重的冲程就越大。因此，对重向上的减速距离为：

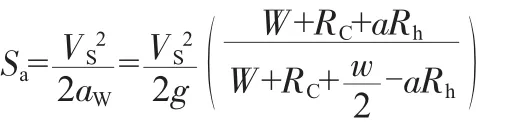
最终主钢丝绳松弛部分的长度为：

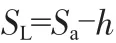
式中，SL为主钢丝绳松弛部分的长度；h为轿厢缓冲器的压缩行程。

所以对重回落后，在拉直（或冲击）钢丝绳时的临界速度为：

3.2 运动工况2分析

直到拉动轿厢为止，钢丝绳将持续被拉伸，此时拉动轿厢的力为：

此时，钢丝绳的延伸量为：

式中，k为主钢丝绳的弹性系数。

当钢丝绳延伸结束时，坠落的对重的速度将从VF减小至V0，当速度达到V0后钢丝绳张力进一步增加将会拉动轿厢向上运动。且该过程中由于弹性产生的势能是不能被忽略的，假设上梁与轿厢绳头是刚性连接，则对重的动能变化为：

重力势能：

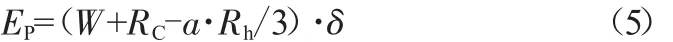
弹性势能：

由于钢丝绳在曳引轮上被拖拽产生位移，因此会有能量损失，摩擦能为：

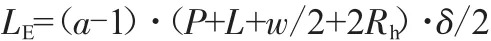
将弹性势能与摩擦能合计为U′：

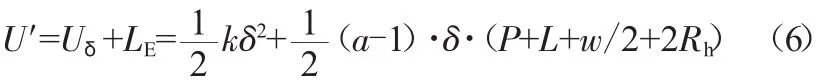
将式（2）与式（3）代入式（6）得：

化简得：

因在测试钢丝绳最大张力过程中发现，钢丝绳的质量相对最大张力不是同一数量级，影响很小，因此略去上式中钢丝绳自重部分得摩擦能：

在运动工况2开始与结束的过程中，能量守恒，则可得：

将式（4）（5）（7）代入式（8）得：

化简得：

3.3 运动工况3分析

对重继续下行距离x1，拉动轿厢上行的距离为x2。

主钢丝绳的张力为：

对重侧的力学平衡方程为：

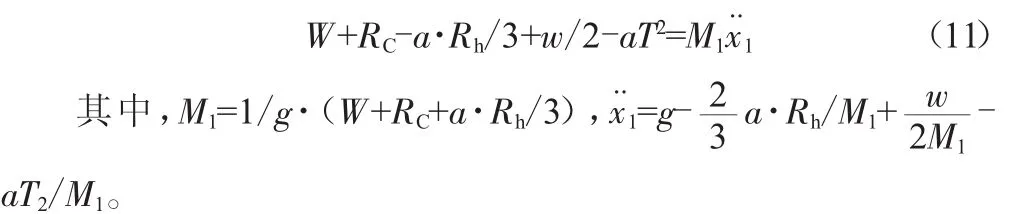
轿厢侧的力学平衡方程为：

由式（10）得：

由式（10）～（13）可得微分方程：

得到T2的通解式为：

其中：

边界条件求解：

取边界条件t=0代入式（14）得：

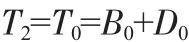
所以：

根据式（10）得：

根据式（14）得：

令：

根据式（17）～（20），且取t=0，得：

所以：

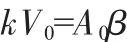
根据式（14）得：

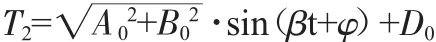
其中：

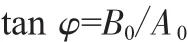
所以：

根据式（15）（16）（21）（22）（23），即可求得在对重回落过程中作用在曳引轮两侧钢丝绳的最大张力。

在设计曳引机、承重机架、钢丝绳等的过程中进行选型和计算时，将上述求得的最大张力作为计算的条件之一，即可得出所需合适的部件。

4 结语

本文尝试利用理论力学知识将由复杂的轿厢压缩缓冲器而产生的对重上抛、停止及回落的过程简化为简单的力学模型，旨在求出由此产生的钢丝绳的最大张力，从而为相关部件的设计提供理论计算依据，保证设计的合理性。