常规桥梁桥墩地震特性及塑性铰分析设计
李 冰
中铁西南科学研究院有限公司,四川成都 610000
在桥梁结构设计中,抗震设计主要有两种,如果是结构较为简单的情况,桥梁设计通常采用的是弹性设计方案,该方案可以很好地满足地震状态下桥梁结构处于一个弹性状态。但是该设计方案只能有效应对地震等级较小的情况,如果遇到较大的地震时,该方案所设计的桥梁就会受到损害。此时可以采用另一个设计方案,即弹塑性的设计,该方案的关键点就是在截面上可以允许桥梁结构发生部分塑性变化的情况[1],进而可以有效改善桥梁节后所承受的极限变形情况,从而适应较大地震所带来的压力。因此,在桥梁结构设计过程中,应合理选用对应的桥墩进行塑性铰设置。
1 模型建立
1.1 分析纤维单元的特性
所谓纤维单元是指大的单元可以继续进一步细分为几个小单元,然后把梁单元具体划分为几个小段,每小段出现轴向变形的情况。在这种单元中,能够准确定出桥梁截面弯矩的曲率关系,尽管与真实结构之间的反应有误差[2],但是尽量控制好误差范围,在有限元软件分析过程中还需要遵守如下三个假定:
第一,分析具体构件发生变形的情况,能够遵循制定的平截面假定,同时还可以掌握纤维变形具体方向以及构件轴线的垂直性;第二,在理论上,主要需要考虑钢筋与混凝土间的荷载作用;第三,结合模型分析而采用梁单元轴心方式连线,并保持一条直线。
在纤维模型单元实施分割过程中,纤维单元中的模型所发生变形与梁截面之间变形一一对应,此外,纤维单元中轴向变形以及梁单元弯曲变形的情况与轴向变形也处于对应状态。但是,纤维单元中应力的状态与梁截面弯矩以及轴力之间的关系可以通过式(1)表示:
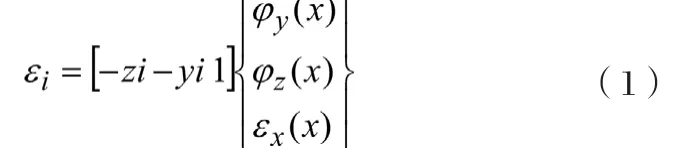
1.2 分析钢纤维本构的模型情况
钢纤维中本构模型通常采用的是双折线型随动硬化,荷载加载的路径以及应变硬化间有一个渐进线区段,即一条曲线,同时还可以明确转移区段中曲线变化情况,如渐近线的交点与加载方向,其在最大应变点所出现的距离变化过程,即变大,然后逐渐平缓。该种本构的关系可以用如下的公式确定:


1.3 分析混凝土本构的模型情况
在桥梁结构设计中,本模型主要是通过受压的混凝土包络曲线公式进行控制,具体公式如下:

2 桥梁情况概述
某地需要建设一座桥梁,长度为455m,桥宽为11.7m,该桥梁在设计阶段需要考虑桥墩地震抗震情况。在本次桥梁设计中可以运用桥梁所专用的有限元软件(即Midas civil)而建立良好的桥梁模型,在本桥的上部结构采用的是I型混凝土梁:3m×30m,下部的结构是T型桥台以及T型桥墩,计划的抗震等级为一级,在完成之后,设计车道主要保障其可以三车进行通行。但是,在设计过程中,桥梁可以很好地应对地震作用所带来整体反应,这就需要设计中对桥梁荷载进行简化处理,并且能够考虑其自重与上部结构之间的二期恒荷载情况。在I型梁中没有充分考虑钢筋以及预应力筋,在研究过程中,重点分析的是抗震中延性构件的桥墩所具有地震反应情况,即桥墩当中的塑性铰受力情况。
桥梁桥墩抗震分析过程中需要把桥梁的自重以及二期的恒载很好地转换成质量的荷载,同时在二号桥墩当中墩柱设计塑性铰区域,并通过纤维分割。在本文中重点分析二号桥墩的墩柱应对地震作用时的具体反应。
3 结果
3.1 分析自振特性情况
通过分析自振特性情况可知,即在本文中主要运用的是Midas软件,具体计算出如下阶段的模态周期与频率,详细分析见下表1。
3.2 分析时程情况
在分析过程中,为了可以更加准确掌握桥梁结构所具有抗震效果,即各个不同的部分发生变形以及内力情况,此时就需要取下墩柱的单元实施时程分析。其中在墩顶处节点的位置按时位移的情况,通过曲线以及内力(即弯矩)得到时程曲线进行表示,桥墩受到地震力作用的影响,桥墩出现较大的晃动,横向位移发生波动,最大的情况下为300mm,而纵桥方向上则为250mm。在上部结构中,横桥向的位移情况非常明显,并且大于纵桥方向的位移,因此,在此大位移的波动之下,比较容易导致梁体的外侧挡块出现破坏的情况,同时还会导致桥梁出现落梁事故。此外,在地震波逐渐减小的情况下,位移波动的情况会越来越小,此时对于桥墩而言就是延性构件,并且在地震当中就可以起到良好的塑性耗能效果[3]。
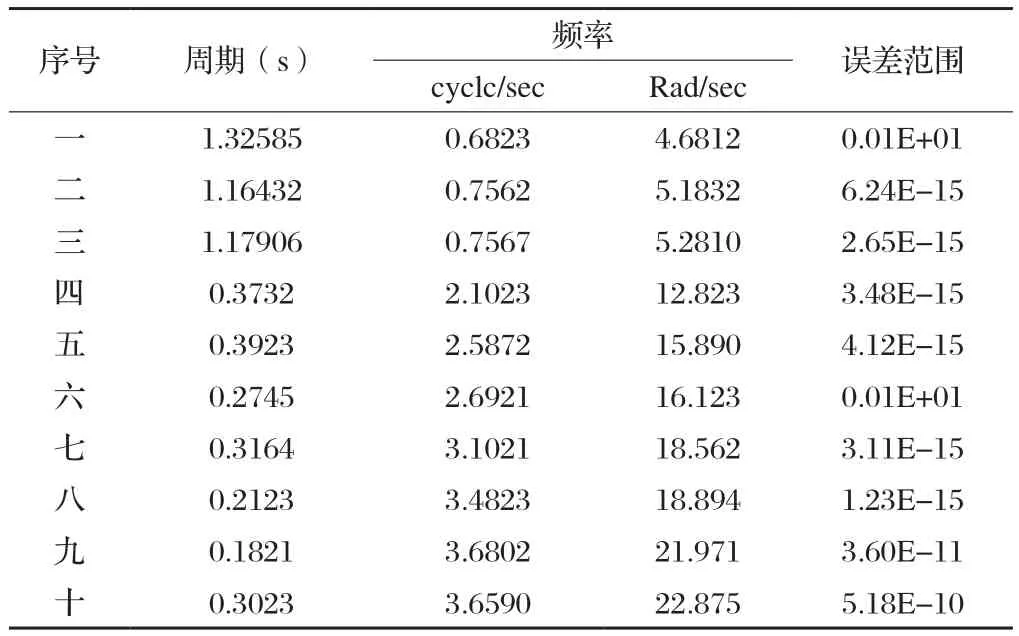
表1 自振特征分析
桥梁中的桥墩柱当中有较大的弯矩,而且在很大弯矩作用之下,通常桥墩会进入一个塑性状态,在今后设计抗震过程中就需要充分考虑其塑性铰,而且还可以充分地发挥出桥墩所具有的耗能作用,这就可以减少桥墩所受到的摧毁压力。
如果桥梁受到较大地震力,此时桥墩顶部就会呈现线弹性的状态,遇到这种情况,墩柱的底部就需要进入一个塑性状态,然后能够在墩柱的中部保持一个紧接的状态能够进入对应的塑性状态,通过塑性铰位置则可以减少桥梁受到的压力。
4 结语
通过上文分析可知,在桥梁结构的设计过程中,抗震设计需要进一步规范,而且能够结合桥梁有限元分析的软件(Midas civil) 分析三跨预应力所承受连续的梁桥压力,可以提升桥梁在地震中其上部结构的梁体横桥,从而很好地提升桥墩抗震能力。

