不同截止高度角下BDS/GPS/GALILEO多模组合SPP 解算性能分析

余晓娜,王超,左小清,布金伟,常军

(1.昆明理工大学 国土资源工程学院,云南 昆明 650093;2.中国人民大学 信息学院,北京 100872;3.国家测绘地理信息局第一大地测量队,陕西 西安 710054)

0 引 言

近几年来,随着导航卫星事业的高速发展,许多国家和地区纷纷建立自己的卫星导航系统[1].目前世界上应用最多的定位导航系统分别是:美国的GPS、欧盟的GALILEO、中国的北斗(BDS)以及俄罗斯的GLONASS.美国的GPS系统经过20多年的研究和实验,于1994年完成24颗卫星在轨的完整系统框架,实现全球98%的覆盖[2].2000年,中国首次建成北斗导航实验系统,北斗卫星导航系统(BDS)计划由35颗卫星组成[3-4],其中有5颗静止轨道卫星、27颗中地球轨道卫星以及3颗倾斜同步轨道卫星.北斗除了在军事方面的应用之外,民用方面也发展迅速,目前基本实现了对东南亚的全覆盖.欧盟的GALILEO卫星导航系统计划于1999年首次公布,由30颗卫星组成,除进行导航、定位、授时服务外,还可以进行搜索与救援.

然而,由于单系统的星座规模有限,提供的定位服务精度低,准确性、可靠性低,安全性有时得不到保障,甚至有时不具实用价值[5].多星座组合导航定位原理与单系统基本相同[6],文献[7-8]对GPS、BDS及其组合系统进行伪距单点定位的研究,表明组合系统的空间分布、定位精度都优于单系统.在观测条件比较恶劣和截止高度角比较高的条件下,三系统组合仍然可以提供定位服务[3-4].

基于一些学者对组合模式的研究,本文开展了不同高度截止角下不同组合模式的伪距单点定位性能分析,主要对BDS(C)、GPS(G)、GPS+BDS(GC)、BDS+GALILEO(CE)、GPS+GALILEO(GC)、GPS+BDS+GALILEO(GCE)六种模式的可见卫星数,X、Y、Z方向上的RMS值以及PDOP值进行详细分析,并比较得出最佳定位组合模式.

1 BDS、GPS、GALILEO组合单点定位模型

1.1 时间系统和坐标系统的统一

1.1.1 时间系统

GPS导航系统的时间系统采用GPS时(GPST),GPST属于原子时系统(AT),其秒长与原子时相同,由于与国际原子时(TAI)具有不同的原点,所以任一瞬间GPST与TAI间有19 s的偏差.GPST的起始时间为1980年1月6日的0时0分0秒的协调世界时(UTC)[9].

GPST与TAI的关系式为

GPST=AIT-19s.

(1)

TAI与UTC的关系式为

AIT=UTC+1 s×n.

(2)

式中,n为AIT与UTC间不断调整的参数.

则GPST与UTC(USNO)的关系式为

GPST=UTC(USNO)+1 s×n-19 s.

(3)

BDS导航系统的时间基准采用北斗时(BDT),BDT与GPST一样也属于原子时系统(AT),基本单位是s.2006年1月1日的0时0分0秒的协调世界时(UTC)为BDT的起算时刻,秒长为原子时秒[10].BDT是通过中国维持的协调世界时UTC(NTSC)与国际UTC建立联系的,由于闰秒的影响,从1980-01-06—2006-01-01日间共有正闰秒+14 s,所以BDT与GPST间相差14 s的整数差[10].

BDT与UTC(NTSC)之间的关系为

BDT=UTC(NTSC)+1 s×n-19 s-14s.

(4)

GALILEO采用GST时,GST时间系统与国际原子钟时间(TAI)同步.

GPST与TAI相差一个常数13 s.[11]

GST与UTC(NTSC)之间的关系式为[12]

GPST=GST-19 s±30 ns.

(5)

1.1.2 坐标系统

GPS采用的是WGS-84坐标系,BDS坐标系统采用的是CGCS2000大地坐标系,GALILEO采用的坐标系统是基于GTRF的ITRF-96大地坐标系.

WGS-84坐标系和CGCS2000坐标系都属于空间大地坐标系,它们的参考椭球面的大部分参数也较为相近,有小部分参数差异造成的坐标偏差很小,在实际计算过程中认为两个坐标系解算出来的结果在实现精度范围内是一致的[13-14].而ITFR-96坐标系与WGS-84坐标系存在的差异为cm级,可以忽略不计,所以在进行非精密测量时三者之间不需要进行坐标转换[15-16].

1.2 BDS+GPS+GALILEO组合单点定位解算模型

单点定位伪距观测方程可以表示为

(6)

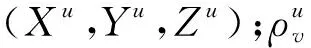
V=AδX-L,

(7)

(f=1,2,…,i+j+k).

式中:i、j、k分别为BDS、GPS、GALILEO的卫星个数;cδtG、cδtC、cδtE分别为GPS、BDS、GALILEO的接收机钟差.

由最小二乘估计计算得[11]:

δX=(ATPA)-1ATPL.

式中：δX为改正数；P为高度角定权.

(8)

2 实验处理与分析

本文选取MGEX跟踪站部分测站的2016年2月1日1天的观测数据,分别对 BDS(C)、GPS(G)、GPS+BDS(GC)组合、BDS+GALILEO(CE)组合、GPS+GALILEO(GE)组合、GPS+BDS+GALILEO(GCE)组合六种方案,在截止高度角为5°、15°、25°、30°、40°、45°的不同情况下进行伪距单点定位,以对结果进行分析.

2.1 不同高度角下多模组合卫星数分析

根据实验,得到了如图1和表1所示的结果.从图1和表1中可以得出以下结论:

表1 不同截止高度角下不同组合的可见卫星数

当可见卫星数目较多时,卫星的空间几何分布越好.表1示出了不同截止高度角(高度角分别为:5°、15°、25°、30°、40°、45°)下,BDS(C)、GPS(G)、GPS+BDS(GC)、 BDS+GALILEO(CE)、GPS+GALILEO(GE)、GPS+BDS+GALILEO(GCE) 六种模式的可见卫星数目最小值和最大值的统计(#表示无法进行定位).图 1示出了不同截止高度角下不同组合系统卫星可见数目的情况.

对于单系统组合,在相同的高度截止角下,BDS(C)的卫星数都比GPS(G)的略多,并且稳定性也优于GPS(G).对于双系统组合,在相同的高度截止角下,GPS+BDS(GC)双系统组合的可见卫星数是三种组合中最多的,最多可达24颗; BDS+GALILEO(CE)双系统组合次之,GPS+GALILEO(GE)双系统组合的可见卫星数最少.GPS+BDS+GALILEO(GCE)三系统组合的卫星数在六种组合模式中是最多的,稳定性也相对来说最高,但是随着截止高度角的增大,卫星数目逐渐减少.从以上数据中我们可以看出,在同一高度截止角下,虽然单系统的卫星数最少,但是仍然满足卫星数最少为4颗的观测条件.

2.2 不同高度角下多模组合RMS值及可用度分析

如图2所示,分别表示了在截止高度角为15°、30°以及40°时的X、Y、Z方向上的RMS值.对于同一组合模式,随着截止高度角的升高,同一方向上的RMS值也随之升高;而对于同一组合模式在相同的高度截止角下,可以得到在Z方向上的RMS值是最小的.在六种组合模式中,GPS+BDS+GALILEO(GCE)三系统组合的稳定性最高,尤其在截止高度角为15°和30°时,稳定性相当,但是在截至高度角为40°时,由于可见卫星数减少,影响了系统的稳定性,所以RMS值增大明显.虽然在X、Y、Z方向上,RMS值都有所增大,但是与其他组合模式相比,是最好的.GPS+GALILEO(GE)组合的X、Y、Z方向的RMS值受截止高度角的影响变化最明显,尤其从30°到40°时,RMS值呈跳跃式增大.对于BDS(C)和GPS(G)单系统组合,BDS(C)的卫星可见数虽然多于GPS(G),但是系统稳定性不如GPS(G).在截止高度角为40°时,由于受到卫星数目的影响,X、Y、Z三个方向的RMS值明显增大,精度降低.

图3示出了不同截止高度角下不同模式的历元可用率.在截止高度角为15°时,BDS(C)、GPS(G)、GPS+BDS(GC)、BDS+GALILEO(CE)、GPS+GALILEO(GE)、GPS+BDS+GALILEO(GCE)六种模式的历元可用率均为96%.在截止高度角为30°时,GPS的历元可用率为87.4%,与高度角为15°时相比下降了9.0%;GPS+GALILEO(GC)组合的历元可用率为90.9%,与高度角为15°时相比,下降了5.3%;而其余组合的可用率与15°时相同,均为96%.在截止高度角为40°时,GPS(G)的历元可用率为47.8%,与高度角为15°时相比下降了50.2%;GPS+GALILEO(GC)组合的历元可用率为56%,与高度角为15°时相比下降了41.7%;BDS(C)单系统的历元可用率为92.2%,与高度角为15°时相比下降了4.0%;其他组合的历元可用率均为96%.

GPS+BDS+GALILEO(GCE)、GPS+BDS(GC)、BDS+GALILEO(CE)三种组合模式的历元可用率不受高度角变化的影响,均为96%.而对于GPS(G)单系统以及GPS+GALILEO(GE)双系统组合,由于受卫星可见数、高度角变化以及稳定性等多种因素的影响,其历元可用率明显降低.

2.3 不同高度角下多模组合的定位精度分析

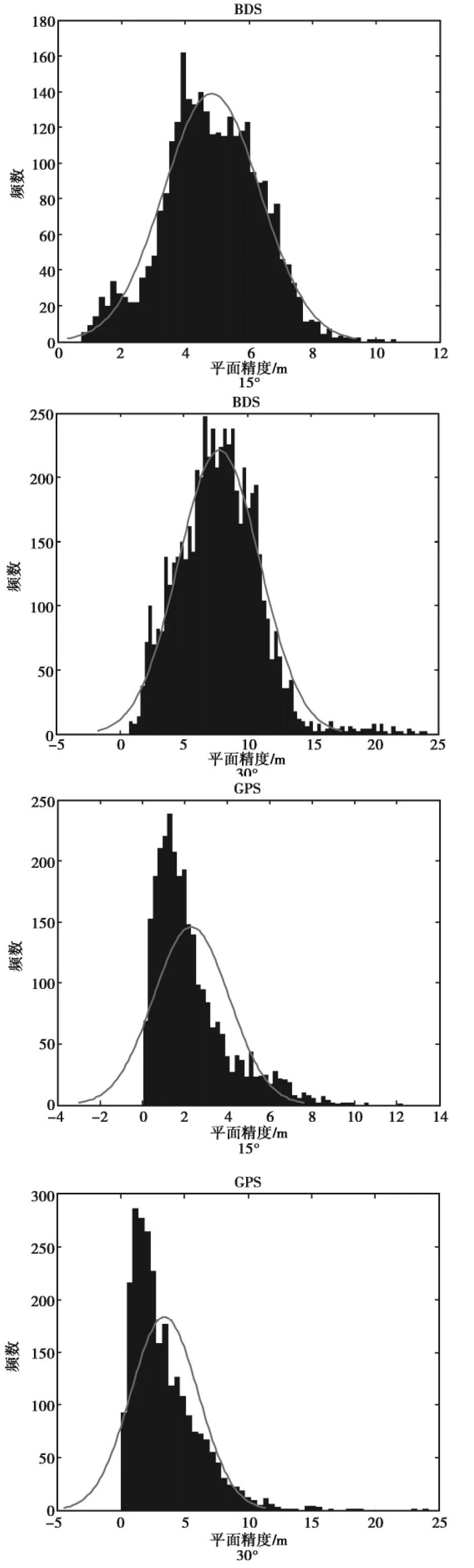
图4 不同截止高度角下不同组合模式的PDOP值

本文选取15°和30°两个不同的高度角分别对六种模式的定位精度进行对比分析,如图4所示横轴表示平面精度,纵轴表示分布频数,其分析结果如下:在高度截止角为15°时,BDS(C)的平面精度为10 m,平面精度和频数曲线的波峰在4～6 m的范围;GPS(G)的平面精度与BDS(C)接近,也是10 m;但是GPS+BDS+GALILEO(GCE)三系统组合的平面精度最高,为8 m.在高度截止角为30°时,BDS(C)、GPS(G)、GPS+BDS(GC)、BDS+GALILEO(CE)、GPS+GALILEO(GE)五种模式的平面精度均降低,但是GPS+BDS+GALILEO(GCE)组合的平面精度不变.

综上所述:对于单系统,随着高度截止角的增大,同一模式的平面精度降低,定位结果较差.可以看出GPS(G)的定位结果比BDS(C)集中,但是平面精度变化很大;对于双系统组合,平面精度的变化情况优于单系统组合,在双系统的三种组合模式中,BDS+GALILEO(CE)组合的平面精度变化相对平稳,并且定位误差都不大,由于受可见卫星数以及历元可用率的影响,可以得出BDS+GALILEO(CE)组合的平面精度在双系统组合中是最高的结论;而对于GPS+BDS+GALILEO(GCE)三系统组合,其平面精度以及频数的变化曲线呈现出标准正态分布的趋势,说明平面精度高,频数分布相对集中.由于可见卫星数增多并且稳定性增强,即使高度截止角升高,但平面精度最高,仍然可以得到可靠且较稳定的定位结果.

3 结束语

本文通过对MGEX跟踪站的CUT0测站和NNOR测站的2016年2月1日1天的观测数据进行试验分析,可以得出以下结论:

1) 在同一截止高度角下,BDS(C)单系统的可见卫星数多于GPS(G),但是GPS(G)的稳定性优于BDS(C).由于受可见卫星数的影响,在同一高度截止角下,GPS(G)的历元可用率低于BDS(C),并且在截止高度角为40°时,GPS(G)的历元可用率不到50%,但GPS(G)的PDOP值和BDS(C)相当.

2) 对于GPS+BDS(GC)、GPS+GALILEO(GE)、BDS+GALILEO(CE)、GPS+BDS+GALILEO(GCE)四种组合模式:在截止高度角为15°、25°时,可见卫星数是最多的,在截止高度角为40°、45°时,由于可见卫星数目较少,其系统稳定性受到严重影响,尽管如此,三系统组合仍然具有较强的定位性能.

3) 高度角的变化对GPS(G)单系统的可用率影响最大,其次是GPS+GALILEO(GE)双系统组合,在截止高度角为40°时,其可用率仅为56%,可见卫星数目下降,稳定性降低.随着高度角的升高,GPS+BDS+GALILEO(GCE)组合在X、Y、Z方向上的RSM值变化不大,定位性能是最稳定的.

4) GPS+BDS+GALILEO(GCE)三系统组合的定位精度在0～8 m之间,远小于单系统和双系统组合,并且频数分布均匀,具有较强的空间几何构型.系统定位的稳定性和可靠性是最优的,与其他组合模式相比,定位精度提高了20%～40%,具有较好的定位服务能力.