蛋形混凝土耐压壳的设计与力学特性研究

朱永梅，戴永健，朱俊臣，张 建,2

(1. 江苏科技大学，江苏 镇江 212003；2. 中国船舶科学研究中心，江苏 无锡 214082)

0 引 言

深海潜水器是进行大洋勘查与深海科学研究的重要运载工具，受到世界各国的普遍重视[1]。耐压壳作为潜水器的关键组成部分，在潜水器的设计开发进程中举足轻重，因此在对海洋的认知、开发过程中耐压壳的研究占有重要位置[2 - 3]。

球形耐压壳体具有强度高、稳定性好等特点，已成为潜水器耐压壳体的首选，但是其空间利用率较低，人们在舱内工作时多数空间不易被利用，造成了较高的空间资源浪费；其次由于其横截面积较大从而水阻系数较高，不便于水下流动作业[4]。蛋壳属于薄壳结构，它的母线是一种正高斯曲线，这种结构不仅能给人一种美学的艺术感，还能节约材料，其次蛋形结构还符合圆顶原理，能够很好地分散来自外在的均布载荷[5]。

混凝土具有抗压、抗腐蚀、抗冻以及防渗透等特性，为其运用于海底建筑建设中提供了保障。通过改变混凝土的水灰比，可以得到不同性能的混凝土材料，这更多的体现了其运用的灵活性[6 - 8]。混凝土结构在海洋建筑中的运用已经非常普遍，如桥梁、堤坝、海上工作台，但将混凝土运用于潜水器耐压壳的建设中，至今仍未见报道。因此，综合考虑蛋壳的耐压性能和混凝土的耐久性，研究并设计能在水下工作的耐压壳结构，可大大节约海洋开发、研究的成本，这不仅对未来海洋资源的开发，还对海军军事发展都显得尤为重要。

本文结合蛋形结构和混凝土的耐压特性，完成2 000 m水深耐压壳的结构设计，分析其在承受均布载荷时，理想状态、考虑初始几何缺陷以及考虑蠕变时的失稳形态以及极限载荷，得出了2年内蛋形混凝土耐压壳的蠕变曲线。

1 蛋形混凝土耐压壳的结构设计

1.1 混凝土配料的选择

国家混凝土结构建设规范根据混凝土的强度划分若干等级，常用的有C20-C50，设计时根据不同的工作环境，选择合适的混凝土强度等级，其中基础在海水里混凝土标号不能低于C30[9]。本文设计2 000 m水深蛋形耐压壳，工程主体建设材料选用混凝土，计算载荷为：

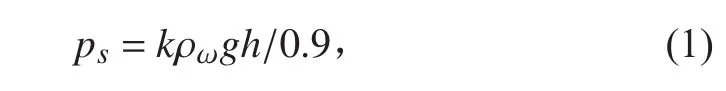
通过计算可得需承受静水压力32.67 MPa，因此，混凝土强度等级初选C35，配料比为：水泥209 kg/m3；砂731 kg/m3；石 1 144 kg/m3；水 152 kg/m3；粉煤灰 95 kg/m3；减水剂 4.490 kg/m3。

常规建筑中混凝土浇筑之后，有必要进行养护，其原因是刚刚浇筑好的混凝土仍处于熔浆质，不具备较高的强度等力学特性，待其硬化后，才能充分发挥混凝土的力学特性。C35混凝土不同龄期抗压强度见表1。C35混凝土养护28 d后，其抗压强度可达到44.62 MPa，用于 2 000 m 水深的耐压壳符合要求，其材料基本参数为：弹性模量，泊松比，材料密度kg/m3。

1.2 蛋形耐压壳的结构设计

国内外球形耐压壳直径一般为2 m，本文采用等体积的设计方法，设计蛋形耐压壳。通过前期的试验研究分析[10]，采用N-R函数[11]作为蛋形耐压壳轮廓设计的数学模型，蛋形耐压壳的体积公式[12]以及蛋形系数公式[12]为：

表1 C35 混凝土不同龄期抗压强度Tab.1 Compressive strength of concrete at different age

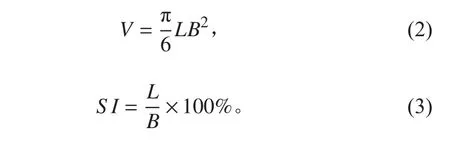
式中：V为体积；L为蛋形耐压壳长轴尺寸；B为短轴尺寸；SI为蛋形系数。

根据对蛋形系数的统计分析，蛋形系数取0.69为最佳。通过计算可得到蛋形耐压壳的长轴尺寸为2.56 m，短轴尺寸为1.77 m。

根据薄壳理论[13-14]，可确定蛋形耐压壳的经向应力和纬向应力，分别为：

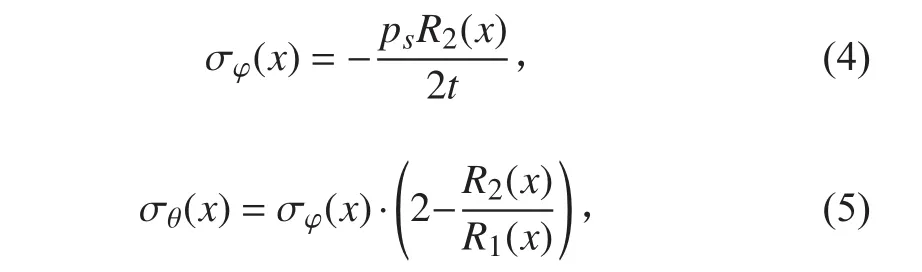
式中：Ps为计算载荷；为第一曲率半径；为第二曲率半径；t为蛋形耐压壳的厚度。

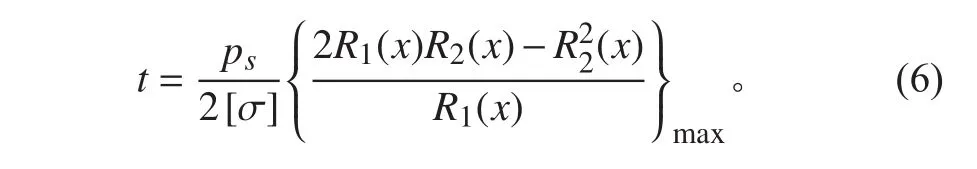
蛋形耐压壳的屈曲临界载荷，采用Mushtari方程[15]表述：

式中：PQ为屈曲临界载荷；μ为泊松比；E为弹性模量；为第一曲率半径均值；为第二曲率半径均值。

综合考虑极限载荷和屈曲载荷，蛋形耐压壳的厚度可由式（8）确定。通过等厚设计方法确定厚度为t=55.29 mm。

2 蛋形混凝土耐压壳力学特性研究

对于耐压壳的力学特性研究，主要集中在强度和屈曲两方面的研究，通过研究2 000 m水深下的蛋形耐压壳最终失稳形式为屈曲失稳[4]。可以认为当耐压壳发生屈曲破坏时，其强度仍未达到极限值，因此本文只对混凝土耐压壳的屈曲展开研究。

2.1 理想状态下蛋形混凝土耐压壳屈曲分析

在混凝土薄壳结构力学稳定性验算方法上，国际壳体和空间结构协会（IASS）推荐了半经验的验算方法，其公式如下：

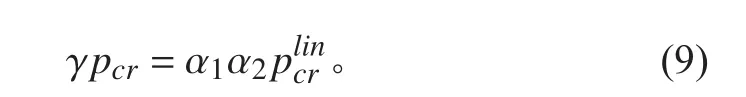
使用三维建模软件根据N-R方程建立蛋形耐压壳轮廓曲线，抽取模型内部保留规定的厚度，得到蛋形壳体结构，使用Ansa软件进行有限元计算前处理，采用网球划分法进行网格划分。由于耐压壳在2 000 m水深下工作，因此其承受均布载荷，理论上模型是不受任何约束力的，但是为了消除模型的刚性位移，在模型中任意选取3点限制模型6个自由度的刚性位移。通过有限元计算可得屈曲临界载荷为51.91 MPa。

图1为蛋形耐压壳一阶线弹性屈曲失稳模式图。

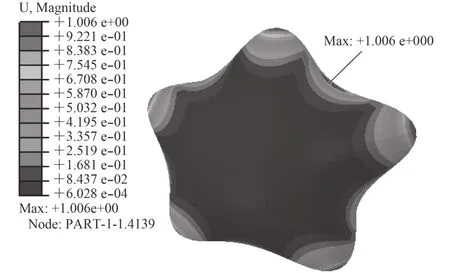
图1 屈曲失稳模式图Fig.1 Buckling model

由图1可知，蛋形耐压壳在外载荷情况下，失稳部位主要发生在中部区域，且呈现波浪状失稳模式，具有5个波峰值，是一种具有正高斯曲线壳的典型失稳模式，沿纬向呈现有规律的凹进与凸出，波峰与波谷数均为5，最大位移出现在如图所示波谷处，值为1.006 mm。

2.2 缺陷状态下蛋形混凝土耐压壳屈曲分析

壳类结构的稳定性对初始缺陷十分敏感，在求解壳类结构稳定性时，初始缺陷必须予以考虑，它能引起壳体临界载荷的下降，无论是在求解线性还是非线性时，初始几何缺陷的特征将十分明显。对于有限元模型，结构初始缺陷的分布趋势，一般可以假设为结构的某一模态或者某几个模态的组成。特征值屈曲模态，是目前非常普遍的计算壳体初始缺陷的一种方法。即假设初始缺陷按照最低阶特征值屈曲模态形式分布。

从开始的理想状态逐渐增大模型的初始缺陷展开研究，分别设置缺陷值为厚度的0.8，0.6，0.4以及0.2倍，研究随着缺陷的增加，模型的屈曲临界载荷的变化情况。

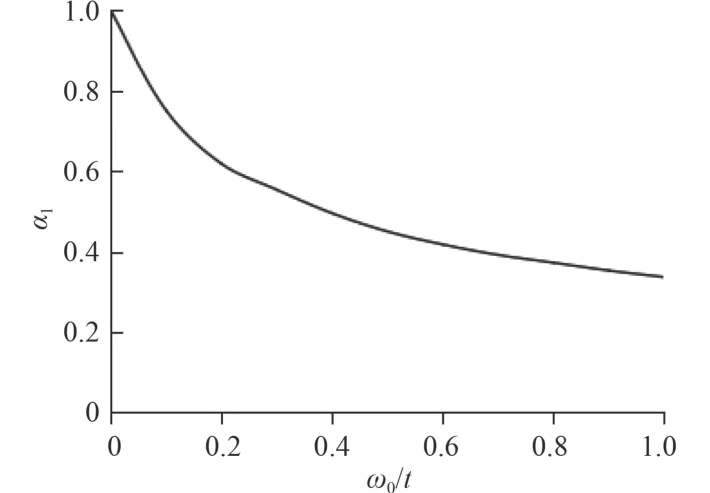
图2 几何缺陷对屈曲的影响Fig.2 The effect of geometric imperfections on buckling

表2 缺陷状态下的临界屈曲载荷Tab.2 Critical buckling load under the condition of imperfections

通过图2可得随着缺陷的增加，耐压壳结构承载能力逐渐降低，屈曲临界载荷不断下降，只是下降的速率不断减小，说明初始几何缺陷对混凝土耐压壳屈曲有一定的影响，相比而言缺陷发展初期对屈曲的影响较大，后期影响较小，这也就是混凝土在裂缝初期对构件的稳定性影响较为显著的原因。

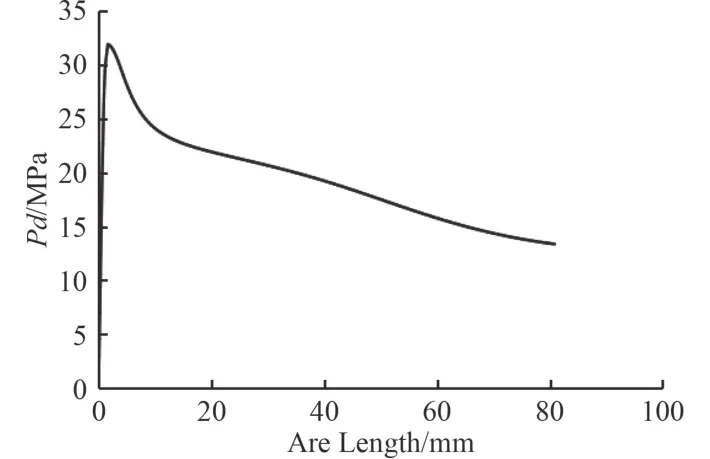
图3 平衡路径图Fig.3 Equilibrium path

图4 为图3中平衡路径末端点的后屈曲失稳模式图，由图可见，混凝土蛋形耐压壳后屈曲失稳模式不同于其线弹性失稳模式，其主要呈现局部凹坑失稳，且失稳部位位于混领土蛋形耐压壳的中部区域，表明蛋形耐压壳中部为危险区域，极易发生屈曲失稳。

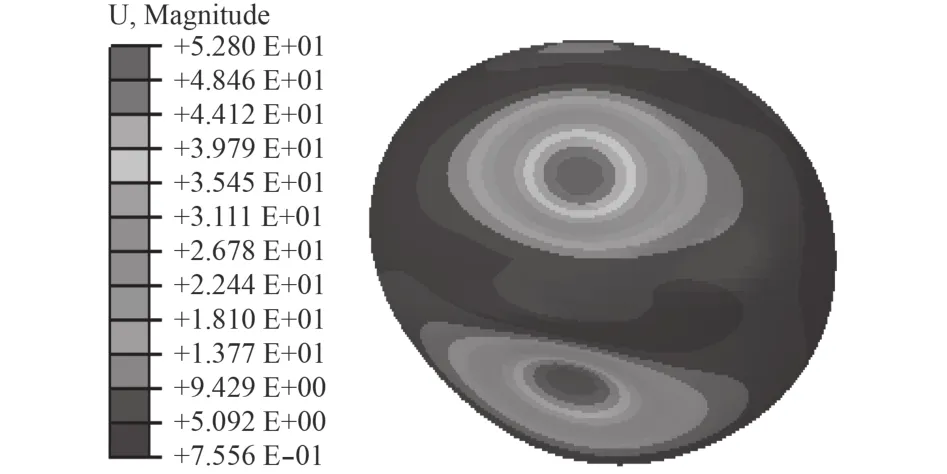
图4 屈曲失稳模式图Fig.4 Buckling model

2.3 混凝土蠕变对耐压壳屈曲的影响

本文使用Abaqus模拟混凝土耐压壳在2年时间内恒定温度下，受到恒定载荷的情况下的蠕变全过程，观察其应力分布、应力应变过程以及屈曲临界载荷。在Abaqus中模型的前处理，如单元类型的选择、网格的划分等都与上文相同，但是材料设置添加了混凝土塑性参数的定义。在Abaqus中，混凝土本构关系由三维模型简化为平面模型，因此在计算时只需要定义混凝土单轴受压的应力应变曲线即可，混凝土的应力应变曲线如图5所示。

在计算蠕变应变时，容差的设置十分关键，它与增量步的大小有着密切的关系，容差越小，增量步也跟着降低，因此在计算时容差值太大会影响精度，太小则会使计算时间变大导致系统崩溃。一般取1E-4～1E-6左右，容差可根据具体计算作调整。本文沿着经线，取蛋形耐压壳结构赤道与钝端之间中点处取一点A，中间赤道部位取点B，赤道与尖端之间中点处取点C。研究随时间的发展各点处的变形情况，结果如图6所示。

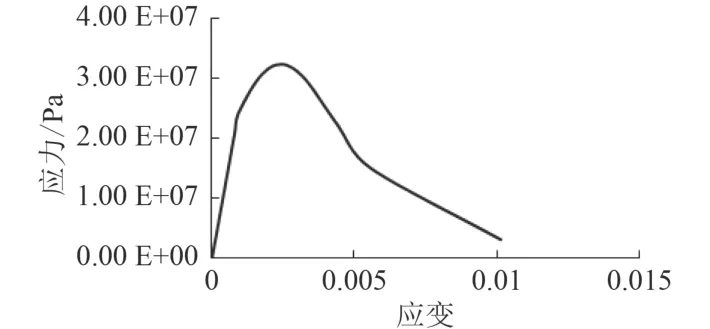
图5 混凝土本构关系曲线Fig.5 The stress-strain curve of concrete

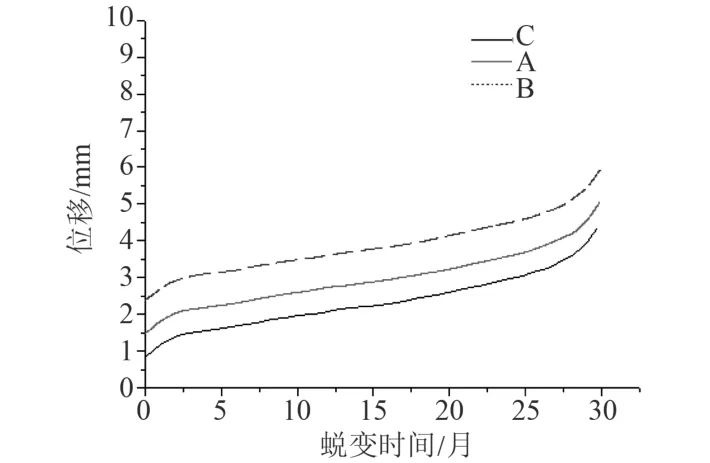
图6 蠕变曲线Fig.6 Creep curve

从图6可看出，随着时间的发展，耐压壳各点处均发生蠕变，但是在相同时间，同等载荷的情况下耐压壳B点处的蠕变发展比A点的大，A点处蠕变比C点大，这也证明了耐压壳内部应力分布规律为赤道处应力比两端大，钝端比尖端应力大；混凝土破坏分为3个阶段，第1阶段为蠕变发展阶段，第2阶段为加速阶段，第3阶段为蠕变破坏阶段，本例在加载2年时间内，混凝土蠕变未发展为第3阶段，因此可以认为未达到破坏极限。最终计算蠕变后屈曲极限载荷为 48.34 MPa。

3 结 语

结合蛋形结构和混凝土的耐压特性，完成了2 000 m水深耐压壳的结构设计，分析了其在承受均布载荷时，理想状态、考虑初始几何缺陷以及考虑蠕变时的失稳形态以及极限载荷，可得到如下结论：

1）耐压壳结构在承受均布载荷时，纬向应力变化幅度大于经向应力，因此设计耐压壳时应重点考虑纬向应力；蛋形结构两端承受的应力较小，中间段承受的应力较大，相比而言尖端承受应力比钝端大，此结果说明失稳最先发生于耐压壳中部，和实验结果相符合。

2）随着缺陷的增加，耐压壳结构承载能力逐渐降低，屈曲临界载荷下降，但是下降的速率逐渐减小，说明在缺陷发展初期对屈曲的影响较大，后期影响较小，此结果说明混凝土在裂缝初期对构件稳定性影响更为显著。

3）随着时间的增大，耐压壳各点处均发生蠕变，但是在相同时间，同等载荷的情况下耐压壳蠕变进展依次为：赤道处，钝端处，尖端处。发生蠕变后耐压壳屈曲极限载荷与理想状态相比下降了6.88%。