一种基于悬臂梁结构的动态推力测量方法
,,,,,
1. 航天工程大学 激光推进及其应用国家重点实验室,北京 101416 2. 西安卫星测控中心,西安 710043
基于多颗微纳卫星的编队、集群、星座,可以承担更为复杂的空间任务[1]。星载微推进器是微纳卫星实现精确姿控、轨控、快速机动的基础。目前,国际上已研制出多种新概念微推进器,如胶体微推进器[2]、激光烧蚀微推进器[3]、脉冲等离子体微推进器[4]、离子推进器等[5],产生的推力通常在微牛至毫牛量级,甚至小到亚微牛量级[6],给微推力的测量带来一定的难度。
目前,推力测量基本都是基于力的动力效果,将推力转换成测量台架的振动幅值或转动位移[7]。按照推进器是否与测量装置固连,可将测量方法分为直接法与间接法[8]。直接法中,推进器固连在测量台架的执行元件上,推力直接转换为测量台架的振动幅值或转动位移,典型装置有扭摆结构[9]、单摆结构[10]、天平结构[11]。直接法精度较高,但由于台架承重推进器,导致固有频率较小,因而响应速度较慢,难以完成推进器设计者十分关注的动态推力的测量。相比之下,采用间接法测量时,推进器与测量台架物理隔离,测量台架固有频率较高,能够较快响应推力变化,实现动态推力测量,同时还可避免供应管路及测控电缆干扰,进行装星后测量,典型装置有吊摆结构[12-13]、弹性盘结构[14]、悬臂梁结构[15-17]。
间接法测量结构中,悬臂梁结构简单,测量时既作为推进器喷射羽流的承接元件,又作为形变元件,通过改变尺寸即可调整工作频带,是应用最广泛的力学结构。目前应用悬臂梁结构时,主要基于静力学模型,依据稳态弯曲量与外力大小的线性关系对推进器稳态推力进行测量[15-17]。而当待测推力动态变化时,悬臂梁振幅较大,难以获得稳态弯曲量,无法解算推力,需要根据悬臂梁动力学模型,得到稳态位移的时变值,进而确定推力测量方法。同时,由于喷射羽流的发散及反射气流对来流干扰等因素影响,悬臂梁测量得到的冲击力与实际推力存在一定误差。文献[17]进行了相应的仿真分析,但受供气软管的影响,试验中只能测量入口压力0.35 MPa以下推力,且精度受限。需要采用精度较高的试验方法,对冲击力与推力关系进行研究,以量化测量误差。
本文在悬臂梁动力学模型的基础上,确定了系统传递函数,根据系统响应特征,确定了动态推力测量方法。同时,通过试验验证了测量方法的正确性,并通过与扭摆测量结果进行对比,分析了测量误差。
1 系统传递函数的建立
单位脉冲函数拉普拉斯变换为1,求得单位脉冲力下的系统响应,做拉普拉斯变换即可求得系统传递函数。
如图1所示,选择悬臂梁未变形时的轴向,即各截面形心的连线作为x轴,选择对称面内与x轴垂直的方向作为y轴。梁的截面尺寸为w×h,长度为l,密度为ρ。采用欧拉-伯努利梁理论,并将阻尼视为线性粘性阻尼。若阻尼系数为c,在单位长度推力f(x,t)作用下,悬臂梁弯曲振动方程[18]为:
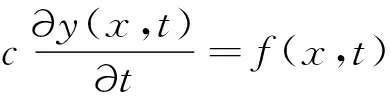
(1)
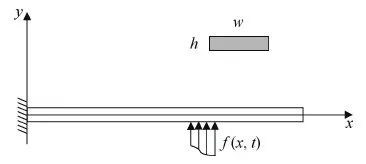
图1 悬臂梁结构模型Fig.1 Cantilever structure model
式中:y(x,t)为x处挠度;E为杨氏模量;I为截面二次矩;ρl为单位长度质量。
悬臂梁振动是由无穷多个主振动的叠加:
(2)
式中:φi(x)、Qi(t)分别为i阶主振动的模态函数、时间函数。i阶固有振动频率ωi为:
(3)
式中:ω1称为振动基频,ωi(i≥2)称为振动高频。βl由频率方程确定:
cos(βl)cosh(βl)+1=0
(4)
模态函数φi(x)为:
φi(x)= cos(βix)-cosh(βix)+
ξi[sin(βix)-sinh(βix)]
(5)
其中,
(6)
为研究方便,将喷射羽流冲击力等效为作用于lf位置处的集中载荷f0δ(x-lf)。悬臂梁初始为静止状态,在位置x=lf处,存在瞬间作用的脉冲力f(lf,t),其瞬间作用冲量为S,单位长度的冲量为Sδ(x-lf)。
将阻尼系数c表示为c=2ρlζiωi,ζi为各阶振动的阻尼比大小,可得系统传递函数G(x,s)为:
(7)
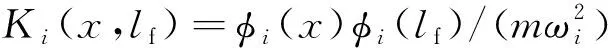
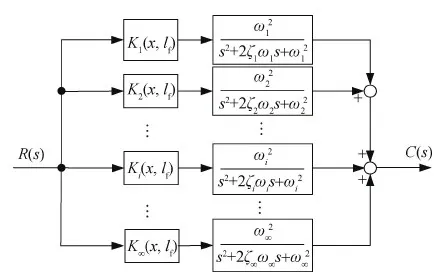
图2 悬臂梁测量系统简化结构Fig.2 Simplified diagram of cantilever measuring system
2 推力测量方法
求得传递函数后,根据阶跃推力f0δ(x-lf)下的系统响应特性,确定推力测量方法。
2.1 阶跃响应特性分析
输入f0δ(x-lf)时,R(s)=f0/s,系统输出为:
(8)
根据式(8),易得f(lf,t)=f0δ(x-lf)作用下,传感器测量位置x=ls处系统响应为:

(9)
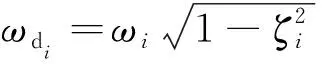
(10)
式(10)表明,yi(ls,∞)与f0为线性关系,线性系数为i阶增益值Ki(ls,lf)。根据式(10),系统稳态位移为:
(11)
由式(11),推力会引起稳态弯曲量变化,稳态弯曲量大小与推力为线性关系,线性系数为系统增益值,系统增益值为各阶子系统增益值之和。
2.2 参数标定及恒定力解算方法
根据式(11),输出恒定标定力f0,悬臂梁振动达到稳态时,测量出y(ls,∞),即可标定出K(ls,lf)。标定出K(ls,lf)后,测量出待测推力的y(ls,∞)后,即可计算出f0大小。但实际测量中,推力作用较短或变化较快时,系统稳态误差较大,无法直接得到y(ls,∞),需要确定y(ls,∞)的求解方法。
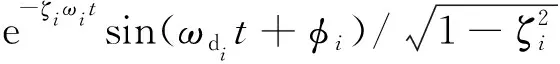
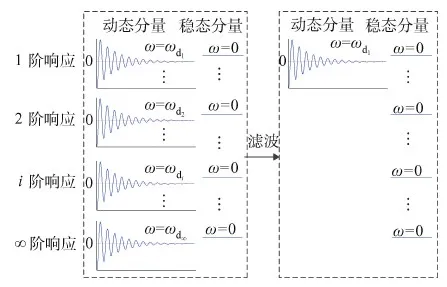
图3 系统阶跃响应低通滤波前后信号变化Fig.3 Signal change before and after low pass filtering of system step response
滤波后,消除1阶动态分量影响,即可得到y(x,∞)。动态分量中,e-ζiωit为衰减项,由于悬臂梁阻尼比较小,通常在10-3量级,在小的时间区间内,动态分量接近等幅振荡。选取1阶响应振动周期Td1作为区间长度,对滤波后系统响应yFilter(x,t)采用末端求均值来估算y(x,∞),如图4所示,推力作用在P2点停止,通过Td1确定区间起始点P1,对P1到P2区间内位移求平均值可估算出P2点对应的y(x,∞)。由于阻尼的作用,动态分量并不是等幅振荡,而是按几何级数衰减,P1到P2区间内均值与y(x,∞)会存在一定误差,显然,推力作用时间tf越大,振幅衰减程度越大,P1到P2区间内幅值差异越小,采用末端均值法估算y(x,∞)精度越高。
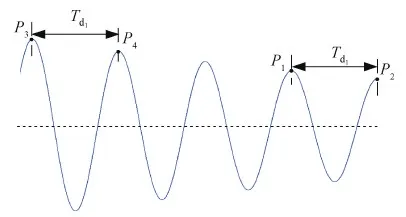
图4 求取稳态位移的末端均值法Fig.4 The end mean method for obtaining the steady state displacement
2.3 动态推力解算方法
当推力变化时,稳态分量y(x,∞)为时变值,动态分量也为时变值,但由于阻尼比不变,采用末端均值法仍可消除动态分量影响,得到时变y(x,∞)。因而,对于系统响应中任意时刻的y(x,∞)求解(等效于推力作用在该时刻停止),向前以Td1为区间进行积分求均值,即可估算出该时刻y(x,∞)。例如,推力作用在图4中P4点停止时,在P3到P4区间内求均值可估算出P4点y(x,∞),根据式(11),即可求解出tf时刻推力。
综合以上分析,tf时刻y(x,∞)估计值可表示为:
(12)
实际中,位移传感器测量得到的响应数据为离散点,传感器采样率为ωs,Td1区间内数据点个数m=ωsTd1,tf时刻对应数据个数n=ωstf,若滤波后系统响应位移数组为yFilter(i),则y(x,∞)估算值为:
(13)
则t时刻推力f0(t)估计值为:
(14)
基于确定的动态推力解算及参数标定方法,可测量步骤如下:
1)标定系统增益值K(ls,lf)。通过施加长时间恒定标定力f0,测量y(x,∞),计算出K(ls,lf)。
2)对系统响应进行滤波,通过末端均值法求出时变y(x,∞),根据式(14),计算f0(t)。
本质上,消除高阶噪声影响后,悬臂梁结构可视为固有频率较高、阻尼比较小的典型的二阶欠阻尼系统进行推力测量。由二阶欠阻尼系统频率响应特性可得,当推力器脉冲频率高于悬臂梁固有频率10倍以上时,稳态输出近似恒定[19],因而仍可采用本文方法测量平均推力。
3 试验验证
通过搭建试验平台,对测量方法进行验证。
3.1 试验平台
测量试验平台由推进器、控制模块及测量模块组成,如图5所示。冷气推进器样机输出推力在微牛至毫牛之间。测量模块由悬臂梁、电动位移台、标定力产生装置(磁铁与线圈)、位移传感器组成,主要作用是将冲击力转变为位移信号;控制模块由位移台控制箱、传感器控制箱及前端放大器、电源、计算机、遥控开关、无线压力接收模块组成,主要用于控制测量模块及推进器工作,接收测量模块输出的位移信号以及推进器输出的入口压力值。
建立测量模型时将推力等效为集中载荷,因而推进器喷口面积要小。测量模块及推进器如图6所示,整个推进器集成于一个平板上,喷嘴直径为1 mm。喷口前压力值表征推进器工况的重要参数,无线压力变送器测量并每隔1 s发送一次喷口前压力值,计算机接收并显示压力值。
悬臂梁(尺寸为210 mm×40 mm×0.3 mm,材料为304不锈钢)与线圈、位移传感器探头通过同一个光学平板固定在电动位移台上,电动位移台用于调节喷口与悬臂梁之间的距离。距离不同会引起喷管内气体膨胀状态的不同,导致作用在悬臂梁上的气体冲击力大小的不同[17]。测量时,悬臂梁的宽度必须能包容全部射流区域。由式(3),悬臂梁振动频率与宽度无关,为了包容全部射流区域,可将宽度做得很大。但宽度增大,会引起系统增益值增大,导致位移量减小,测量灵敏度降低。因而理论上,宽度选择应为满足包容全部射流区域的最小值。冷气喷管出口扩张角度为12°,距离变化最大值为100 mm,计算得宽度最小值为36.3 mm。为留有一定裕度,选择宽度40 mm。粘贴在悬臂梁上的磁铁(Φ6×1.5 mm,质量0.29 g,材料为N35)与线圈(30匝)构成标定力产生装置。经过电子天平标定,线圈电流0.1A时,电磁力大小为0.511 mN。位移传感器为电容式位移传感器(分辨力30 nm,量程1 mm),可以直接以数字量形式输出悬臂梁响应位移大小。
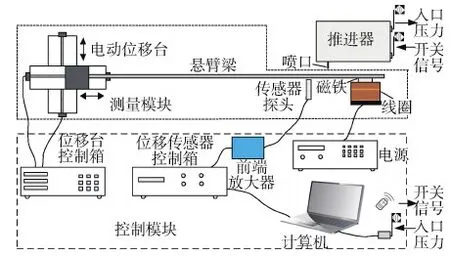
图5 基于悬臂梁结构的推力测量平台结构Fig.5 Structure map of thrust measurement platform based on cantilever structure

图6 基于悬臂梁结构的测量系统Fig.6 Measuring system based on cantilever structure
3.2 试验结果
首先通过施加电磁标定力标定出系统增益值,然后控制推进器输出推力,得到系统位移响应,采用末端均值法求取时变稳态位移值,结合标定出的状态增益值,求取时变推力。
3.2.1 系统增益值标定
标定中,设置位移测量臂长ls=106 mm,采样率ωs=1041.7 Hz,标定力f0力臂lf=174 mm时,控制线圈电流依次输出0.1 A、0.2 A及0.3 A,对应f0为0.511 mN、1.022 mN及1.533 mN(斥力),然后逐渐减小到0.1 A时,系统响应如图7所示。
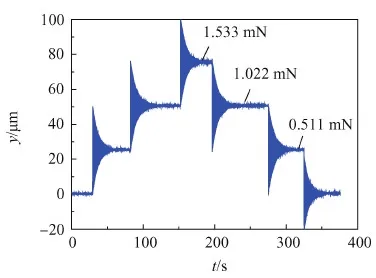
图7 标定力逐渐增大、减小时悬臂梁响应Fig.7 Response of cantilever when gradually increasing and reducing the calibration force
图7中,标定力作用下,系统经过动态振动,最终稳定在新的平衡位置,稳定时间约为50 s。卸载标定力后,系统回到初始平衡位置,表明系统零漂较小。不同大小f0稳态位移y(ls,∞)分别为25.3101 μm、60.6212 μm、75.6327 μm,根据式(11),可得系统增益值K(ls,lf)=4.953×10-2。
3.2.2 推力测量结果
推进器作用力臂lf=135 mm,喷口入口压力0.45 MPa。悬臂梁与喷口距离24 mm时,系统响应如图8所示。推力作用下,悬臂梁开始弯曲振动,平均位置基本稳定在90 μm左右。在20 s之前,振幅整体上呈现衰减趋势;20 s之后,振幅基本稳定,但波动较大。推进器停止工作后,悬臂梁开始自由振动,振幅逐渐衰减,最终稳定在初始平衡位置。推力停止输出后,悬臂梁振幅按指数规律衰减,而推进器工作时,振幅波动明显大于环境噪声,说明振幅的波动是由推力输出的不稳定引起的。虽然存在振幅的波动,但平衡位置并没有发生变化,说明推力输出不稳定为随机突变式,相当于脉冲力的作用,因而不会引起平衡位置的改变。对图8进行频谱分析得到ωd1=6.401 6 Hz,ωd2=40.879 1 Hz,设置滤波时截止频率为8 Hz。
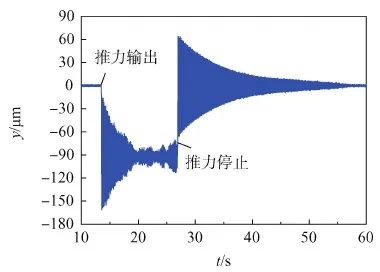
图8 推力作用下系统响应曲线Fig.8 System response curve under thrust
采用末端均值法,根据滤波后响应曲线求取y(ls,∞)随时间的变化与响应数据的对比如图9所示。y(ls,∞)整体上保持平稳,并存在较小的波动。y(ls,∞)平均值为-92.013 5 μm,标准差为0.979 6 μm。

图9 推力响应与求取的稳态位移对比Fig.9 Comparison of thrust response and the calculated steady state displacement
由于K(ls,lf)=4.953×10-2,根据式(11),计算得到的推力随时间变化曲线如图10所示。推力开始作用的初始0.5 s,推力逐渐增大,而后逐渐平稳。计算得推力平均值为2.584 mN,标准差为0.028 mN,推力相对于平均值的最大变化不超过0.080 mN。
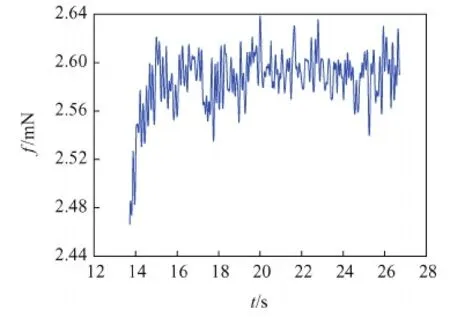
图10 推力随时间变化曲线Fig.10 Thrust curve in variation of time
4 误差分析
采用非接触测量方式时,由于发散及反射气流对来流干扰等因素影响,实际上悬臂梁测量得到的是尾流冲击力,与实际推力存在一定误差。将作用在悬臂梁上的冲击力的测量误差记为US1,冲击力与实际推力误差记为US2,推力测量误差记为US。
4.1 冲击力测量误差
首先来分析US1大小。式(14)中,K(ls,lf)标定误差来源包括y(ls,∞)求取误差,以及标定力f0本身的输出误差。y(ls,∞)误差等于位移传感器测量误差0.050%。设置相同采样率及悬臂梁参数进行理论计算,滤波所对应的幅值计算误差为-0.470%。综合位移测量及滤波误差,可认为y(ls,∞)误差为:
(15)
标定力误差为1.210%,标定及冲击力解算中均需要求解y(ls,∞),则认为:
(16)
4.2 推力与冲击力关系
在相同的测量环境及推进器工况条件下,采用试验手段,以精度较高的扭摆系统的测量结果为推力基准,与悬臂梁测量结果进行对比,分析得到US2。
显然,当喷口与悬臂梁距离变化时,冲击力大小也是不同的。在2~100 mm之间,保持入口压力0.45 MPa,以回进程方式,通过电位移台逐渐增大、减小距离,每隔2 mm测量5次取平均值,得到的冲击力及误差值如图11所示,随着距离变化,冲击力大小变化明显,最大值约为最小值的3倍。

图11 推力测量值随喷口与悬臂梁距离的变化Fig.11 Measured thrust in variation of distance between nozzle and cantilever
按照冲击力变化规律,将距离分为3个区段:
1) I区段为冲击力上升段(2~24 mm),冲击力随着距离的增大而增大,尤其是10~14 mm区间内,冲击力快速增大,较小的距离差值也会引起冲击力的明显变化,因而测量误差也相对较大。
2) II区段为冲击力平稳段(24~42 mm),冲击力随距离变化较小,平均值为2.597 mN,变异系数为0.49%。在此区间内测量时,能够测量得到较为稳定的冲击力值,然后得到该区间内冲击力与实际推力的关系。测量推力时,首先测量得到冲击力后,根据确定的关系即可计算出实际推力。
3) III区段为减小段(42~100 mm),冲击力随着距离的增大而减小,且区间内误差较大,可能的原因是距离较大时,尾流扩散时易受随机误差影响。
通过减压阀调整入口压力,得到平稳段位置基本保持不变,说明喷口形状一定时,冲击力平稳段位置也是一定的。得到冲击力与距离关系后,以下通过扭摆来测量实际推力大小。
扭摆原理如图12所示,推进器与配重在扭转横梁的两端平衡。旋转横梁与转轴固定,转轴通过上下两个挠性枢轴(用于提供回复力)与固定部件相连。推进器输出推力时,推力转化为横梁的线位移,随着位移的增大,推力与枢轴回复力逐渐趋于平衡。位移传感器测量横梁稳态线位移,结合电磁标定力标定出的扭转刚度系数,即可解算出推力大小。
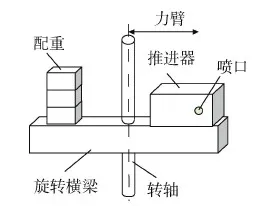
图12 扭摆测量推力原理Fig.12 Thrust measurement principle of torsion balance
标定得到,扭摆有阻尼振动周期为11.910 s,振动频率为8.40×10-2Hz,阻尼比为0.283。相比之下,扭摆系统的阻尼比、振动频率均比悬臂梁大2个数量级。施加1.063 mN标定力后,控制推进器输出推力,扭摆系统响应如图13所示,推力作用下,扭摆响应特性为二阶系统典型阶跃响应。
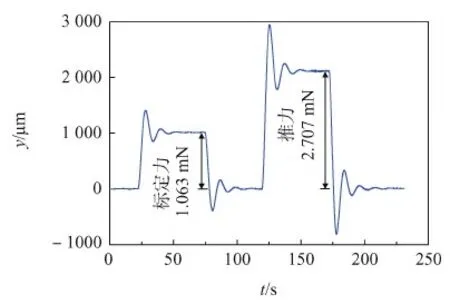
图13 标定力响应与推力响应对比Fig.13 Response comparison of calibration force and thrust
结合标定出的刚度系数,同时考虑测量臂长及推力力臂比例关系在内,并考虑扭摆测量误差,解算得推力大小为2.707 mN。保持测量条件不变,经过5次测量,计算得推力平均值为2.707 mN,标准差为9.85×10-3mN。因而有,悬臂梁测量结果小于扭摆测量结果,平均值相差-4.06%。也就是说,在平稳段测量得到的冲击力与实际推力误差为-4.064%,因而US2=-4.064%。
同时,对比图13与图8可得,扭摆系统振动频率较小,对于高频扰动具有一定的抑制作用,而悬臂梁振动频率较大,响应较快,能够响应推力输出不稳定波动。
确定US1及US2后,可得悬臂梁结构测量推进器阶跃力误差US:
(17)
5 结束语
本文确定了基于末端均值法求时变稳态位移,进而计算动态推力的方法,得到的主要结论如下:
1) 悬臂梁测量系统在结构上为无穷多个欠阻尼二阶子系统的并联,系统增益值与刚度系数大小为倒数关系。
2) 悬臂梁系统阻尼比较小,位移响应中的动态分量在较小的时间区间内接近等幅振荡。通过低通滤波消除高阶动态分量的影响,以一阶振荡周期为区间长度求平均值可消除动态分量影响,得到精度较高的稳态位移时变值。
3) 悬臂梁与喷口之间距离对冲击力影响较大,随着距离的增大,冲击力先增大后减小。在一定距离区间内,会出现一段平稳区,在此区间内进行测量,可以得到稳定的冲击力数值。入口压力0.45 MPa时,在距离为24~40 mm区间内,出现冲击力稳定区,推力平均值为2.597 mN,变异系数为0.49%。
4) 与扭摆测量结果对比得到,冲击力测量值小于实际推力。推力测量误差由冲击力测量误差及冲击力与真实推力之间的误差组成。
结合仿真分析,研究射流与悬臂梁之间其他作用形式对测量结果影响,以及进一步细化误差分析,是下一步的研究重点。

