贵州赤水常绿阔叶林不同层次树木空间分布格局和竞争的关系
张昊楠,薛建辉
1 南京林业大学生物与环境学院,南京 210037 2 环境保护部南京环境科学研究所,南京 210042 3 江苏省中国科学院植物研究所,南京 210014
植物种群内个体的空间分布与形成该种群的生态学过程联系紧密[1- 2],对其空间分布格局研究不仅能够描绘植物个体分布格局,而且有助于对产生这种分布模式的生态学过程(如种内和种间竞争、种子扩散、干扰等)的进一步理解[2- 5]。竞争是形成特定群落结构、构成分布格局的基本驱动力之一,树种的空间分布和大小并不是相互独立的,而是广泛受到竞争过程影响[6-7]。检测群落中竞争的一个重要方法是使用空间点格局分析法对森林空间分布模式生成“快照”(snapshot),将其二维特性保持不变。如果竞争在森林群落构造中是一个重要的工作机制,则有以下两个假设:(1)树木个体的大小会与最近邻域距离呈现正相关关系。(2)相比于早期的演替阶段,树种空间分布会随着时间变化而趋于均匀分布[8- 12]。这种现象不仅在相同年龄段的树种、相同物种的纯林中出现,在林龄不同、物种不同的混交林中,以及不同高度层次的树种中也会发生[8]。例如,古田山中亚热带常绿阔叶林中的优势树种甜槠 (Castanopsiseyrei)与木荷(Schimasuperba)在空间上主要呈聚集分布, 且随年龄阶段的增加, 聚集程度有降低的趋势[12];喀麦隆热带森林群落内的中、下层树在0.5 m的尺度下主要呈现出均匀分布,而演替时间较长的上层树种则呈现出随机分布的格局[8]。在森林的垂直结构中,占据着不同高度级别的树种个体获得光照、水分等资源的机会不同,通过空间点格局研究方法描述其分布格局,分析其个体和群体在空间上的相关关系,对理解森林垂直结构中不同高度层次林木在不同资源配置状况下如何竞争和共存,形成不同的生活策略具有重要意义。
理解竞争对植物空间分布格局的贡献和其导致的变化是一项重要挑战[7],有时,竞争的强度、空间异质性或斑块性会导致空间格局分布模式与竞争间的关系模糊不清[10],这时则需要采用更加灵敏的方法来检测。标记点格局分析[13-14]使用能够反映树木生长情况的一些连续的附加信息(胸径、树高、冠幅和生长量等),并结合个体间的距离来分析群落内的竞争[15-17]。相比于单一依靠树木间的距离进行检测,标记点格局分析能够检测到森林群落内细微的竞争,可在植物个体空间分布上呈现出更加丰富的生长信息,这对于研究植物种群特定空间格局的形成机制和演替中相邻个体间的竞争非常重要[8]。
本研究中,我们将树种个体按照树高分级(林木下层、中层、上层),使用基于距离和标记的空间点格局分析方法,检测样地面积为0.96 hm2的常绿阔叶林群落中层内和层间竞争对树种空间分布和生长的影响,采用树种的胸径(Diameter at Breast Height, DBH)和冠幅(Crown Width, CW)做为附加标记来衡量不同个体生长状况,主要研究以下两个问题:(1)赤水地区常绿阔叶林样地中,不同高度级别的树木空间分布格局的普遍性规律和特点。(2)竞争在不同高度层次树种个体间的大小和产生的原因。赤水桫椤国家级自然保护区地处亚热带,物种丰富,而目前该地区物种共存机制的研究仍然较少,研究其群落中植物个体空间分布和竞争具有重要意义。
1 材料与方法
1.1 研究区概况
本研究样地设置具体地点位于贵州赤水桫椤国家级自然保护区,其始建于1984年,位于贵州省赤水市与习水县交界,紧邻赤水河畔,总面积为13300 hm2,属野生植物类型自然保护区,以桫椤(Alsophilaspinulosa)、小黄花茶(Camellialuteoflora)及其生境为主要保护对象。研究地区属于中亚热带湿润季风气候区,河谷具有类似南亚热带气候特征,大于10℃活动积温为4200—5100℃,大于10℃天数200—230 d,最冷月(1月)均温2.0—5.0℃,年降水量1200—1300 mm,相对湿度86%—90%。土壤的发育深受地层与岩石性的制约,主要为非地带性的紫色土,多为中性和微酸性,发育成熟且土层较深厚,海拔800 m以上地区也局部分布有由紫色砂页岩残留古风化壳母质发育而成的黄壤和黄棕壤。植被类型上,樟科、安息香科、山茶科和桦木科等常绿乔木在保护区海拔700 m至1455 m区域处于优势地位,是典型的中亚热带常绿阔叶林,但在一些次生性的林内,亦有部分落叶树种如亮叶桦存在[18]。
1.2 研究方法
1.2.1 样地设置
2015年在研究区建立1个0.96 hm2固定样地(80 m×120 m),样地中心海拔922 m,样方设置和空间定位方法按照《生物多样性观测技术导则-陆生维管植物》(HJ 710.1- 2014)的样地建设规范[19],并参照巴拿马(Barro Colorado Island)50 hm2热带雨林样地建设技术规范和经验,用森林罗盘确定样地的方向和基线,然后用全站仪将固定样地划分成20 m×20 m小样方,用卷尺、测绳或便携式激光测距仪将进一步将每个20 m×20 m的小样方划分为5 m×5 m小样方,这些5 m×5 m样方作为胸径(DBH)≥1 cm乔木和灌木的基本观测单元进行每木检尺记录树种,测量树高(Tree height)、胸径(DBH)和冠幅(CW),按照不同树高将样地内树种分为上层、中层和下层3个高度层次[8],其中树高小于或等于5 m的为下层树种(lower),树高在5 m和10 m之间的为中层树种(intermediate),树高大于10 m的为上层树种(upper)。样地内主要树种包括细枝柃(Euryaloquaiana)、亮叶桦(Betulaluminifera)、米槠(Castanopsiscarlesii)等亚热带常绿阔叶林常见树种,由于该地区在20世纪80年代保护区建立前存在一定的人类活动,群落内还包含了赤杨叶(Alniphyllumfortunei)、杉木(Cunninghamialanceolata)等次生先锋树种[18],其中赤杨叶共有312株个体,杉木有143株个体,主要占据了群落中下层的空间,而上层空间主要被毛脉南酸枣(Choerospondiasaxillaris)和亮叶桦等大树个体占据(表1),样地内群落空间分布格局见图1。
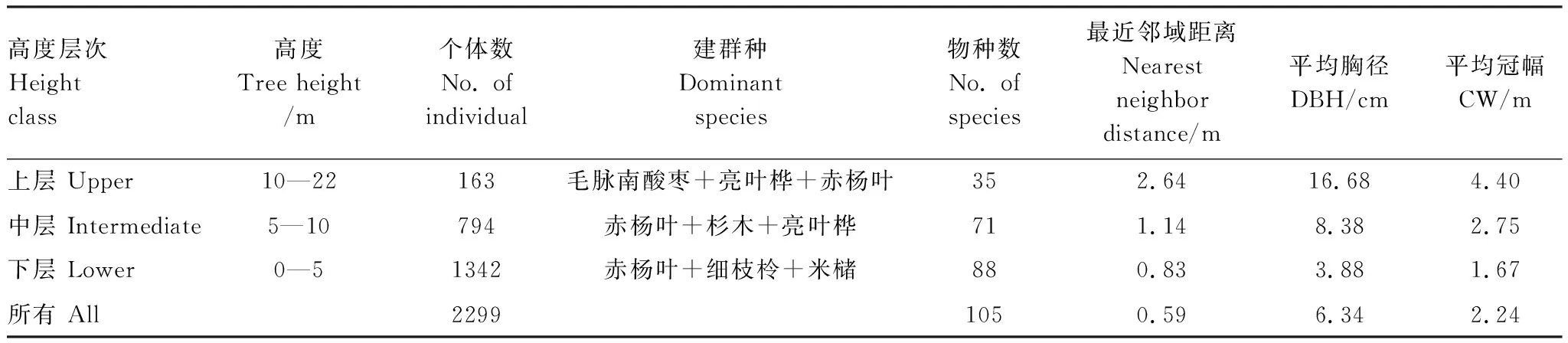
表1 3种高度层次下树木种群的数量特征

图1 基于树高、胸径和冠幅标记的样地内所有植物个体空间分布示意图Fig.1 The stem maps of individual tree species in three height classes示意图中菱形代表树高,圆形代表胸径,矩形代表冠幅,浅灰色代表上层树种,深灰色代表中层树种,黑色代表下层树种,不同标记的大小代表不同个体树高、胸径和冠幅的大小
1.2.2 空间统计方法
基于距离的空间点格局分析
基于距离的空间点格局分析使用g函数,其中,同一高度层次内树种空间分布格局研究拟采用单变量点格局分析方法g(r)来进行,其采用Ripley′s K函数转化而来[20],公式如下:
它是用指定宽度的圆环区域取代了Ripley 的k函数中半径为r的圆形区域,因此它是一个概率密度函数[20- 22]。不同高度层次主要树种的空间关联使用双变量多元点格局分析方法gij(r)来进行,通过计算以样地内不同高度层次内树种个体i在以自身为圆心、半径为r的圆环区域内树种个体j的分布数量来分析植物个体i和j的相关关系[20],其中个体i和j是群落中不同高度层次中两个任意个体。在本研究的单变量分析和双变量分析中,若g(r)=1,则同一高度层次中植物群落的分布格局为随机分布(Complete Spatial Randomness, CSR)或者距离为r的不同高度层次中的物种i和物种j的个体在空间格局上无关系;若g(r)>1,则同一层次内植物空间分布格局聚集性分布或不同高度层次中的个体呈现正相关关系;若g(r)<1,为均匀分布或负相关关系。对测试结果进行Monte Carlo 拟合以检验其显著性。本文还计算了样地内不同高度层次树种的最近邻域距离(Nearest Neighbor distance,NN-dis)。
(2)基于距离和个体属性的标记点格局分析
经典的空间点格局分析方法仅基于距离来描述树种个体间的空间结构,然而,树木个体的胸径、树高、冠幅和生长量等附加信息,在空间上往往存在相关关系,例如在个体间相互抑制的情况下距离较近的植物个体的大小会低于整个群落的平均水平[15],所以对于同一种类型的植物群落来说,单变量标记点格局分析可以用来检测种内竞争。标记点格局分析同样可以拓展为双变量分析[23],可以用来研究两种类型植物间潜在的竞争。
本文以群落的树高、冠幅作为标记属性,采用单变和双量标记点格局分析方法研究同一高度层次内和不同高度层间的植物个体空间分布格局关系,使用k函数进行计算,其可以用来探索因为密度效应引起的植物个体在生长上的降低[13-14,21],公式如下:
式中,t(mi,mj) 是植物个体的标记mi和mj的假设检验函数[13],对于单变量分析,mi和mj分别是同一高度层次中两个植物个体的胸径和冠幅;对于双变量分析,mi和mj分别是不同高度层次中的标记。对于单变量和双变量标记点格局分析,当kmi,mj(r)=1时,距离为r的物种i和j的标记之间没有相关关系;当kmi,mj(r)>1时,两者呈现正相关关系;当kmi,mj(r)<1时,标记之间为负相关关系,即距离为r的两植物个体i和j的胸径或冠幅的大小低于整个群落的平均水平,当个体i和个体j表示不同高度级别中的两个乔木个体,其结果可以用来检测不同高度层次内的层内竞争和层间竞争。测试结果同样进行Monte Carlo 拟合检验。
1.2.3 Monte Carlo 拟合和零模型选取
本文运用Monte Carlo 拟合检验计算上下包迹线,用种群实际分布数据计算得到不同尺度下的g(r)值以生成置信区间,对于不同检测来说,在单变量分析中,若检测结果在包迹线之间为随机分布,高于上包迹线为显著聚集性分布,低于下包迹线为显著均匀分布;在双变量分析中,若在包迹线之间表示两类格局或标记为无关联,高于上包迹线为显著性正相关,低于下包迹线为显著性负相关。针对不同空间分析有针对性的选取零模型类型是十分重要的,因为选取不恰当零模型来进行Monte Carlo拟合往往会导致对空间格局错误的解释。
对于单变量距离点格局分析,首先对样地内所有物种的混合分布格局进行检测,若发现不存在强烈的聚集分布,选取完全随过程(CSR)作为零模型的模拟点分布过程;若发现大部分点聚集分布于样地的部分空间内,则使用基于异质泊松过程的零模型[24]来进行Monte Carlo拟合以形成置信区间。选取异质泊松过程是因为本研究样地受到第一序列异质性的影响,密度λ并不是一个近似于常数的值,而是随着(x,y)的位置在样地内不断变化,因此运用宽度为R的圆形的移动窗口在样地内进行插值计算,估计出λ(x,y)的值,代表空间的一阶特征。本研究发现中层和下层的树种在较大尺度上出现了聚集分布,说明其分布格局上存在一定的异质性,故采用泊松异质模型(Heterogeneous Poissonprocess, HP)。在双变量距离点格局分析中,研究样地内不同层次树种年龄并不一致,其树高大小的分类实际上是定义其不同年龄群系的一种代指,是来自于不同过程所产生的空间分布模式的一种 “先验”,因此将其看作两种独立的类群,采用种群独立零模型(Population Independence, PI)进行置信区间的拟合[25]。在标记点格局和变异系数分析中,我们将群落中的树高标记随机标记在树木个体上,通过Monte Carlo方法不断拟合以探索树群落中高标记潜在的空间结构的置信区间[8],故采用完全随机零模型(CSR)。
本研究中Monte Carlo 拟合检验采用拟合次数设定为为199次,即95%置信区间。使用空间统计学软件Programita、R语言软件和Excel软件对数据进行分析统计和作图,其中R语言软件所使用的程序包主要包括spatstat 1.48[26]、ads[27]等。
2 结果与分析
2.1 不同高度层次树种空间分布格局
基于距离的单变量点格局分析发现本研究样地群落内3种不同高度层次物种在小尺度下主要呈现聚集分布格局(图2),其中上层树种在0—40 m的尺度下基本呈现空间随机分布格局(图2),而中层和下层树种分别在0—6 m和0—4 m的尺度下聚集分布(图2)。同时,研究还发现乔木上层树种个体间的最近邻域距离(2.64 m)远大于中下层个体,说明上层树种个体在群落空间内的距离要比中下层树种大。上层树种与中、下层树种在单一基于距离的个体空间点格局分布上的差异,表明不同高度层次树木正处于不同演替阶段,上层树种的随机分布格局可能是由于其在长期演替中相邻个体间的竞争导致。

图2 3种高度层次(上层,中层和下层)下基于距离的单变量点格局分析和基于胸径(DBH)、冠幅(CW)的单变量标记点格局分析Fig.2 Distance-based and mark (DBH, CW) -based Univariate spatial point pattern analysis in three height classes黑色线条和黑色圆点代表单变量g函数和K函数在不同距离尺度下的数值,灰色线条代表Monte Carlo 拟合检验形成的上下包迹线即置信区间
2.2 不同高度层次内树种标记空间分布格局与层内竞争
基于胸径和冠幅的单变量标记点格局分析发现,样地中不同尺度下不同胸径和冠幅在上层树种内呈现出随机分布格局(图2),而中层树种内的胸径和冠幅分别在0—7 m和3—6 m的小尺度下(图2)出现了显著负相关关系,下层树种内的胸径和冠幅分别在1—2 m和7—14 m的小尺度下(图2)出现了显著负相关关系。随着尺度的增加,中层树种的胸径和冠幅逐渐呈现正相关关系,分别在27—29 m和28—29 m的尺度下(图2)出现显著正相关关系。这表明本研究中上层树种个体间胸径和冠幅的标记在全部尺度下没有显著的空间相关关系,即未检测到两者间的竞争。而距离较近的中层个体间胸径和冠幅的标记呈现出显著的负相关关系,即相邻的中层植物个体间在生长过程发生了相互影响,植物个体间的竞争降低了距离较近个体在胸径和冠幅上的生长。下层植物个体表现出和中层植物个体内一致的层内竞争现象。
2.3 不同高度层次间树种标记空间分布格局与层间竞争
基于胸径和冠幅的双变量标记点格局分析发现,群落内上层植被和中层、下层植被在全部尺度上基本没有相关关系(图3),而中层和下层树种在胸径和冠幅上都在0—10 m的小尺度下(图3)呈现出显著的负相关关系。这表明在群落空间中距离较近的成对的中层和下层树种,其胸径和冠幅的大小要小于整个群落的平均水平,说明小尺度下相邻的中下层树种存在相互影响、相互抑制的关系,群落的演替中产生的层间竞争会影响距离较近的不同高度层次间树木个体的大小(胸径和冠幅)。此外,对群落胸径、冠幅与树高的相关关系分析发现,上层树种的胸径和树高相关关系要强于中、下层树种,而冠幅与树高的相关关系无明显变化规律(图4),这说明随着高度的增加,群落内树木个体的胸径生长受到的影响逐渐减小。

图3 3种高度层次(上层,中层和下层)下基于距离的双变量点格局分析和基于胸径(DBH)、冠幅(CW)的双变量标记点格局分析Fig.3 Distance-based and mark (DBH, CW) -based Bivariate spatial point pattern analysis in three height classes黑色线条和黑色圆点代表双变量g函数和K函数在不同距离尺度下的数值,灰色线条代表Monte Carlo 拟合检验形成的上下包迹线即置信区间
基于距离的双变量点格局分析发现,不同高度层次下树种在小尺度下主要呈现显著的正相关关系,上层和中层(图3)、中层和下层在0—1 m的尺度下(图3)呈现显著正相关关系,而上层和下层树种中没有检测到显著的相关关系(图3),这表明在1 m以内的小尺度下上层和中层、中层和下层树种距离较近,即没有检测到层间竞争。同时,对于群落内中、下层树种层间个体的相关关系,基于胸径和冠幅的双变量标记点格局分析结果与基于距离的双变量格局分析结果相反(图3),这表明不同的方法对本研究中树木个体层间竞争关系的检测结果可能不同,两者间竞争关系有待进一步讨论和解释。
3 讨论
3.1 群落上层树种空间分布格局与影响因素
很多研究表明[28- 31],森林中较为高大的树种(乔木上层)几乎在所有尺度下呈现随机或者均匀分布,而较小级别(乔木中、下层)的树种在小尺度下呈现聚集分布格局,其原因被解释为上层树种的均匀、随机分布来自于对光照、水分和养分等资源的竞争[32- 35]。本研究基于距离的单变量点格局分析结果也呈现出类似的现象,即在群落中聚集分布距离较近的树木个体主要是中、下层树种,而上层树种在长期演替后基本呈现出随机分布格局。此外,基于胸径和冠幅的单变量标记点格局分析均未检测到上层树种存在层内竞争,双变量点格局也未发现上层树种与中、下层树种存在层间竞争关系(图3),即在当前演替阶段上层树种与群落中其他个体的竞争关系表现为非常微弱。显然,一旦群落中的乔木树种超过一定的高度尤其是超越了中、下层树种的林冠层高度后,将更多的获得阳光等其他自然资源,群落内的竞争对其产生的影响会下降至次要因素,其分布格局也主要呈现随机分布[8]。本研究中上层树种胸径与树高的相关关系比中、下层树种更强的结果也支持了这种解释(图4),这说明随着高度的增加,树种生长受到的影响逐渐减小。据牛克昌等报道[36-37],群落构建可以被认为是物种被筛选的过程,而环境条件和生物间的相互作用可以被看作是多个嵌套的筛子。因此也可以认为,研究样地在群落构建中对不同高度层次树种进行了环境筛选,导致了树高相似的树种个体被筛入相同的生态位[37-39],群落中物种的特征趋同现象通过形成不同高度层次的树种得以表现,光照等自然资源可能是发生这种环境筛选的主要控制因子[8,24]。

图4 不同级别树高和胸径、冠幅的相关关系图Fig.4 Correction between diameter at breast height (DBH) and tree height for the three size classes, and between crown width (CW) and tree height, respectively○代表上层树种,□代表中层树种,△代表下层树种
3.2 群落中下层树种空间分布格局与竞争
使用单变量和双变量标记点格局分析发现了研究样地内中、下层树种的层内和层间个体均表现为显著的负相关关系,竞争导致了群落内距离较近的中下、层树种的个体大小(胸径和冠幅)要小于群落内的平均水平[15],即较小的个体距离更近,较大个体距离较远。这种现象可以解释为中、下层树种对环境资源的需求相近,所采取的生活策略类似,在同一层次内和两种不同层次间都表现为相互竞争的关系,例如距离较近的且根系深度相似的个体,对群落内有限的水分、养分等自然资源相互争夺[8]。本研究中树种(中、下层)在单变量格局中小尺度下聚集分布的特点也是竞争对不同树种生长的影响在空间格局上的一种表现。值得注意的是,基于距离的双变量点格局分析并未检测到群落内各层级树种间的竞争关系,发现群落内各层植物间在小尺度下呈现显著正相关或无相关关系(图3),尤其是中、下层树木呈现显著的正相关关系,这与标记点格局检测到结果不相一致。同时,基于距离的单变量点格局分析发现中、下层树木主要呈现聚集分布,并未出现在竞争导致空间分布格局趋于更加规则化[8- 12]的现象,对此解释为:(1)标记点格局分析要比单一基于距离的点格局分析更为灵敏,能够检测到物种间较为微弱的竞争。对于样地中、下层植物来说,竞争强度尚不足引发树种的大量死亡从而导致树种空间分布剧变,而仅是对树种的生长产生了影响,这种影响在本研究中主要反映在胸径增粗和冠幅扩大上,所以中、下层树种的层内和层间竞争也仅在以胸径和冠幅为标记的标记点格局分析中检测到;(2)对上层树种而言,竞争会导致大树死亡,产生的林窗会导致后代(中下层树木个体)更新呈现聚集分布格局[9,40],Getzin等[6]曾报道过在未成熟和过熟的花旗松种群中,竞争和树种的聚集度呈正相关关系。据此,认为本研究中随着不同层次个体大小的增加,最近邻域距离从上层树种到下层逐渐降低(表1),中、下层树种个体在有限空间的竞争进一步加剧,导致了个体较小的中下层更新树种在层间和层内都出现了小尺度下聚集分布格局,从而在单一基于距离的单变量和双变量分析中都呈显著的正相关关系。
综上所述,本文研究发现在贵州赤水地区常绿阔叶林群落中不高度同层次树种处于不同的演替阶段,群落中的竞争对个体较大的林木上层物种的影响较弱,而主要发生在中、下层林木的层次内和层次间,这表明在该地区亚热带常绿阔叶林中下层个体对资源、环境因子具有相似的需求,解释了群落中3种高度层次间树种竞争与共存的不同策略。同时,我们验证了标记点格局在检测群落微弱竞争中的敏感性,尤其是对于强度不足以引发大量树种死亡而剧烈改变树种空间分布格局,而对树种本身胸径增粗和冠幅扩大等生长量属性产生影响的情况;相对于单一依靠距离的空间点格局分析,标记点格局分析更能准确的反映群落不同层次、不同个体间的相互关系和个体属性。这在评价和研究森林种群及个体健康程度,确定森林经营的合理密度等生产实践中具有重要指导意义,对理解植物个体属性的空间分布、不同种类及层次的树木个体间的竞争和共存机制等方面具有重要理论价值。

