基于门限递归单元循环神经网络的交通流预测方法研究

王体迎，时鹏超，刘蒋琼，刘博艺，时天昊

(1. 海南大学 机电工程学院，海南 海口 570228； 2. 海南大学 热带农林学院，海南 海口 570228; 3. 海南大学 信息科学技术学院，海南 海口 570228； 4. 山东科技大学 交通学院，山东 青岛 266590)

0 引 言

随着社会经济的高速发展，城市交通拥堵问题越来越严重，交通管理遇到了前所未有的挑战。经验证明，单一的路网改造和传统的交通管理模式已经不能有效地解决交通拥堵问题。为了缓解交通网络所面临的巨大压力，智能交通系统(intelligent transportation systems, ITS)受到了前所未有的重视，得到了快速发展。其被认为是治理汽车尾气排放污染、缓解交通拥堵的核心技术，也是减少交通事故发生的有效方法。而有效、准确的交通流量预测是确保智能交通系统成功部署的关键要素，得到了越来越多的关注[1]，其一方面能够为出行者提供实时的交通信息，从而帮助他们更好地规划路径，另一方面为管理者提供了交通数据，以便更好地做出决策，进行适时交通诱导，缓解道路拥堵，实现高效、节能、环保、安全、舒适的交通运行环境[2]。

1 研究现状

自20世纪80年代以来，人们为了提高改善交通运行效率，提高预测效果，开发了许多交通流量预测模型[3]。大体来说，可以分为两类：一类是以数理统计和微积分等传统数学和物理方法为基础的预测模型[4]；另一类是以现代科技为研究手段而形成的预测模型。第1类模型追求周密严谨上的数学推导和通俗易懂的物理意义。时间序列模型(time-series model)[5]是第1类中的典型代表，如被广泛使用的自回归模型(autoregressive model, AR)，自回归积分滑动平均模型(autoregressive integrated moving average model, ARIMA)[6]，这类模型技术成熟，但容易受随机因素的影响，需要大量不间断数据。如卡尔曼滤波模型(kalman filtering model)[7]，精度较高，鲁棒性较好，但需要大量矩阵计算；历史平均模型(history average model)[8]，算法简单，可解决部分简单场景下的交通流量预测问题，但不能有效地应对具有非线性特性的动态交通流量以及突发事件；第2类模型侧重于对真实情况的拟合效果。如非参数回归模型(nonparametric regressive model)[9]，其不需要先验知识，只需有足够的历史数据，但复杂度较大；许岩岩等[10]应用于交通流量预测的分类回归树，预测结果较好，可解释性强，但参数调整需要一定的技巧性；小波神经网络模型[11]比普通神经网络具有更快的收敛速度和更高的预测精度，但是需要有足够的经验才能选择合适的小波基函数；支持向量机[12]可以克服过拟合的缺陷，但是对大规模训练样本难以实施；高斯过程回归[13]不仅可以预测交通流量值，还可以获得预测方差的估计值，但需要先对数据进行平稳化处理，不利于实时预测。

虽然目前已经有了很多交通流量预测模型，但是大部分都是比较简单的模型，且并不总是稳定。这就启示我们要基于大量交通数据并从数据挖掘层次来重新思考交通流量预测问题[1]。

最近，机器学习中的深度学习获得了举世瞩目的成功，得到了学术界和工业界的广泛关注[14]。其已经成功的应用于分类任务、自然语言处理、降维、目标检测、运动建模等[15-18]。深度学习是一种多层描述的表征学习，在输入数据后，深度学习算法从低级到高级、逐级地获取隐藏于数据内部的特征[1]。实际上，交通流量过程是复杂的时间序列，深度学习算法中的门限递归单元(gated recurrent unit, GRU)[19]循环神经网络(recurrent neural networks, RNN)，能够不依靠先验知识，对交通流量建模并进行很好的预测。

2 门限递归单元

门限递归单元是长短期记忆单元(long-short term memory unit, LSTM)[20]的一个改变较大的变体，而长短期记忆单元则又是循环神经网络里一种特殊的神经层。

RNN网络是包含循环的网络，其具有“记忆性”。与传统的神经网络和最近大受欢迎的卷积神经网络(CNN)[21]不同的是，RNN可以利用“序列信息”。在结构上表现为，隐藏层的输入不但像普通神经网络一样包括上一层的输出，还包含上一时刻隐藏层的输出，即隐藏层节点之间也是具有连接的，从而完成了对前面信息的记忆，并使之影响当前的输出。从理论上讲，其能够利用的序列信息可以为任意长度的。

不过传统的RNN在训练长期依赖(long-term dependencies)的时候会遇到很多困难，最常见的就是梯度消失(vanish gradient)问题。期间有很多解决方案被提出，大致可分为3类：第1类是以新的方法改善传统的权重随机初始化，使用一个有关联的矩阵初始化；第2类是使用新的激活函数，如修正线性单元(rectified linear unit，ReLU)[22]替代传统的sigmoid函数；第3类是使用设计更精妙的循环单元，如LSTM，GRU等。

1997年，S. HOCHREITER等[20]提出了LSTM，其改进了普通RNN的隐藏层，经过3个不同的门来接合前面的状态、当前的输入和当前的记忆，然后使用了不同的函数来计算隐藏层的状态。实践证明，LSTM对长期依赖问题非常有效。2014年，K. CHO等[23]对LSTM进行了改进，提出了更易于计算和实现的GRU。

设rt是GRU在时刻t的重置门(reset gate)，计算公式如下：

rt=σg(Wrxt+Urht-1)

(1)

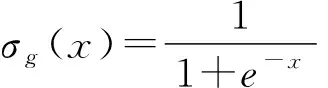
同理，设zt是GRU在时刻t的更新门(update gate)：

zt=σg(Wzxt+Uzht-1)

(2)

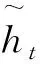
(3)

(4)

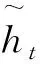
另一方面，更新门zt控制有多少ht-1中的信息可以传递到当前ht中。这一点是该单元结果的设计关键，其作用与LSTM中的记忆单元(memory cell)相似，可以帮助RNN记忆长期信息。

每个GRU都会学习获取不同时间尺度的依赖信息。更新门zt的值较大的GRU会获取较为长期的依赖信息，而重置门rt的值较大的GRU则相反，会获取较为短期的依赖信息。

图1为GRU的结构简图，显示了GRU结构中各个门之间的关系。图2为GRU神经网络在时间维度上的展开，显示了相邻时刻的GRU神经网络之间的相互作用。

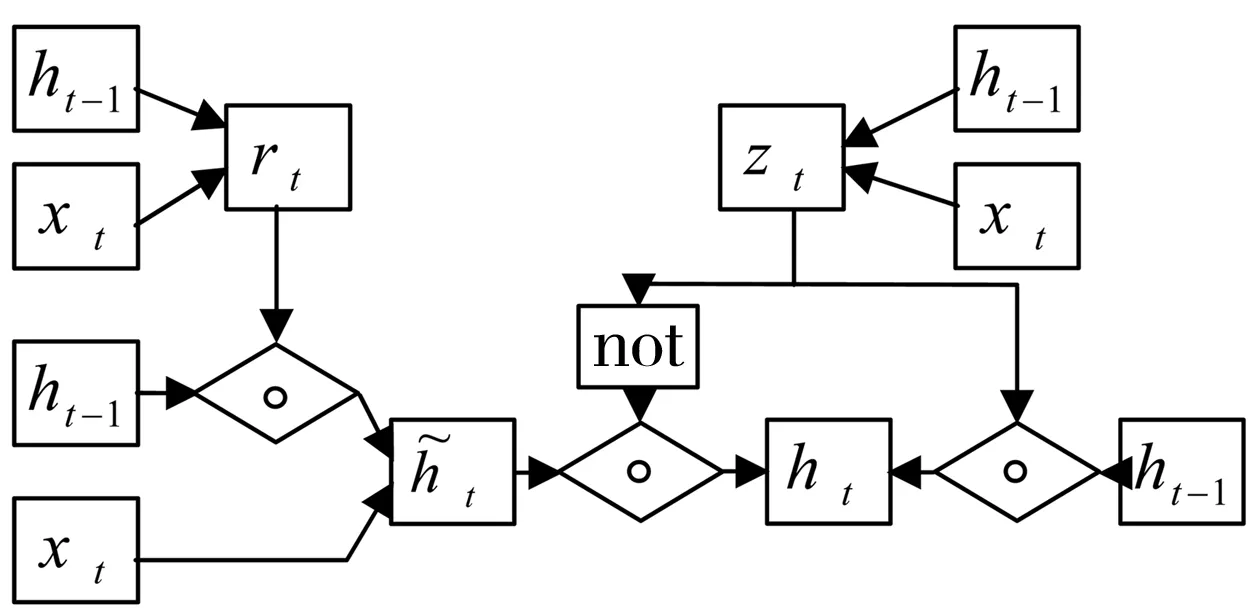
图1 GRU的结构Fig. 1 GRU architecture

图2 GRU神经网络的展开Fig. 2 An unroll GRU neural network

模型的输入量可用x=(x1,x2,x3,…,xT)表示，模型的输出可用y表示。在交通流量预测问题中，可将x定义为当前和历史时刻的数据，其可包含多个数据维度，如交通流量、车流速度、交通事故、天气状况、节假日等。笔者只选取交通流量进行研究，所以x=qt-N,qt-(N-1),…,qt。模型将基于输入的数据x以及GRU的历史输入信息输出预测结果y，即下一时刻的交通流量qt+1。

具体步骤如下所述：

Step1：将交通流量整理为合适的输入格式并进行预处理，使用最小最大标准化(min-max standardization)技术将其映射到[0,1]之间；

Step2：确定GRU神经网络的结构，如GRU层数，每层神经元数目；

Step3：选择合适的激活函数和恰当的优化算法；

Step4：采用训练集数据对神经网络进行训练优化，得到预测模型；

Step5：使用验证数据集验证模型预测效果。如效果良好，继续预测则进入Step 5，否则返回Step 2；

Step6：利用预测效果良好的模型和测试数据预测得到对应的交通流量预测值。

通过以上6个步骤可实现使用GRU神经网络对交通流量的预测。

3 数据分析和模型建立

为了测试GRU对交通流量的预测效果，笔者采用了加拿大大不列颠哥伦比亚省所公开的交通流量数据集来测试。选取了16-032E观测点和16-032W观测点所采集到的数据，两点只是监测车流方向不同，但位置相同，都位于大温哥华地区的列治文市，测点部署位置如图3。

图3 观测点的部署位置Fig. 3 The location of the observation point

对所采集到的数据资料中有极少部分缺失或异常的现象进行如下处理：对于异常的数据，如交通流量过低的数据，将其从数据集中清除；对于缺失的数据，使用缺失数据之前的数据进行填充，以保证数据集的连续性和有效性。数据采集时间间隔为1 h，采集时间从2001年1月1日到2003年12月31日。为了验证模型的预测效果和更公正的对比不同模型的准确性，数据集被分为两个部分，从2001年1月1日到2002年12月31日，共730天，作为训练集，用来确定模型的参数：从2003年1月1日到2003年12月31日，共365天，作为测试集。方便起见，笔者的GRU模型基于python下的Keras包实现，运行环境为Ubuntu 16.04，64位操作系统，Intel i5 4200M 2核心4线程CPU，8G内存，GeForce 840M GPU。

图4展示了两个观测点中训练集的一周交通流量。由图4可以看出，交通流量很明显具有以天为周期的模式。周一至周五的流量模式大致相同，说明交通流量具有一定的规律性。而不同观测点观测到的交通流量之间呈现出不同的数据特性，如16-032E的工作日流量模式含有两个流量高峰，其中第2个高峰远远高于第1个高峰，16-032W的工作日流量模式虽然也含有两个流量高峰，但是第1个流量高峰大于第2个流量高峰，表现出了两个观测点的方向性。不同观测点的相异的交通流量模式要求我们针对不同观测点训练不同的模型，以适应其模式变化。

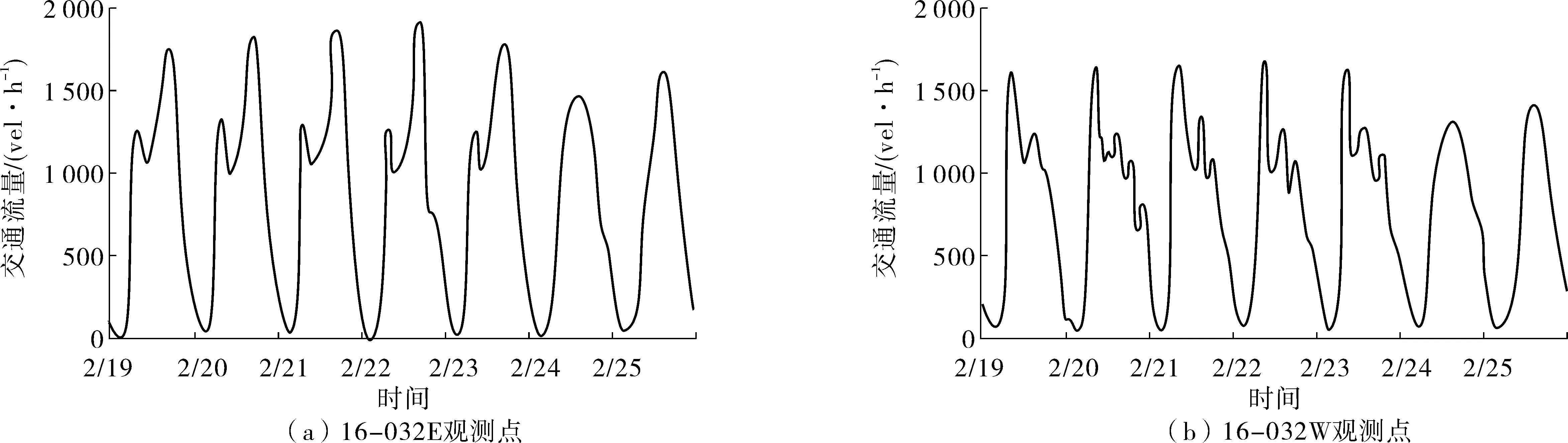
图4 观测点一周的交通流量Fig. 4 Weekly traffic flow of observation point

4 实验结果分析

笔者将实验结果与传统交通流量预测方法进行对比：用差分自回归移动平均模型(ARIMA)和支持向量回归(SVR)预测模型对同样的测试序列进行预测。对于神经网络，笔者使用Adam[24]作为参数优化方法。对于SVR模型，笔者选择使用径向基函数(radial basis function, RBF)作为核函数，使用交叉验证(cross-validation)和网格搜索(grid search)相结合的办法选取模型参数：惩罚参数C(cost)，径向基的宽度参数γ(gamma)，不敏感参数ε(epsilon)。根据赤池信息量准则(akaike information criterion, AIC)，选择最佳的ARIMA模型的p,d,q参数。

为了更好的对比不同模型的预测效果，笔者将基于不同滞后时间(time-lag)的输入数据进行测试，如24个滞后时间(过去24 h的交通流量)、18个滞后时间(过去18 h的交通流量)、12个滞后时间(过去12 h的交通流量)以及6个滞后时间(过去6 h的交通流量)。

为了评价预测效果，采用了两种误差评测方法，均方误差(MSE)和平方绝对百分比误差(MAPE)，其定义公式如下：

(5)

(6)

表1表示了不同模型在不同观测点位置，以不同滞后时间输入数据下不同评价标准的预测性能指标。

表1 使用MAPE和MSE对不同模型在各观测点的预测性能比较Table 1 Prediction performance comparison of the MAPE and the MSE for different model

根据仿真的实验结果可以发现，一般来讲，输入的滞后时间越长，模型越能获得更好的预测效果。在16-032E观测点的数据集上，GRU在24个滞后时间的输入数据上取得的预测结果比在6个滞后时间上取得的预测结果在MAPE方面下降了16.77%，而MSE方面则下降了47.81%。SVR模型也有类似的效果。

从表1中可以看出，基于GRU的神经网络能够取得比SVR和ARIMA更高的预测精度。对于16-032E观测点的数据集的4个不同滞后时间的预测任务，GRU模型预测效果稳定，取得了10.07%的平均MAPE值，相对于ARIMA的37.61%的平均MAPE值和SVR的11.76%的平均MAPE值，分别降低了73.22%和14.37%。而对于16-032W的数据集的4个预测任务，GRU的平均MAPE则比相对应的ARIMA的平均MAPE值和SVR的平均MAPE值，分别降低了76.22%和9.93%，即使是在下降最低的18个滞后时间上，也相对于ARIMA至少下降了61.46%。而在平均MSE值方面，则分别下降了89.85%和20.77%。

作为神经网络的主要竞争者，SVR模型表现良好，甚至在某些特定情况下，预测效果超过了GRU模型。然而在寻找最优滞后时间方面SVR模型表现并不是太理想。ARIMA模型假设交通是个静态状况，而这一点在现实生活中往往并不能成立。

图5、图6分别展示了GRU模型在不同滞后时间输入数据下，对两个观测点工作日和休息日条件下两种交通流量模式的实际预测效果。因为周三受到周末的交通影响最小，笔者选取周三作为工作日交通流量模式的典型代表进行展示。又由于周日不像周六那样容易受周五交通流量影响，故而选取周日作为休息日交通流量模式的典型代表进行展示。图5表明GRU模型可以很好的应对16-032E观测点观测到的周三和周日两种交通流量模式，预测的交通流量和实际交通流量误差较小，可以很好的抓住交通流量的基本规律。不论是早高峰还是晚高峰，模型都能很好的预测出其出现时间和峰值。图6表明的是16-032W观测点周三和周日交通流量的预测效果。由于16-032E和16-32W是为了测量同一条道路不同方向交通流量而设置的两个对称观测点，故而16-032W和16-032E观测到的周三交通流量具有呈对称性的方向不均匀性。而两观测点观测到的周日交通流量都具有相似的波峰、波谷变化趋势。通过对图5、图6的分析，可以获知：随着输入数据滞后时间的增加，预测的流量曲线与实际流量曲线的吻合度也在不断增加，但是增加速率缓慢，即在不同滞后时间输入数据下，GRU模型仍能保持对流量的准确预测，表明模型具有较高的预测稳定性，不易受到输入数据滞后时间大小的影响。

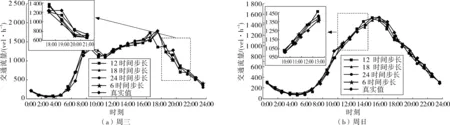
图5 对16-032E观测点周三和周日交通流量的预测比较Fig. 5 Prediction performance comparison for 16-032E in Wednesday and Sunday

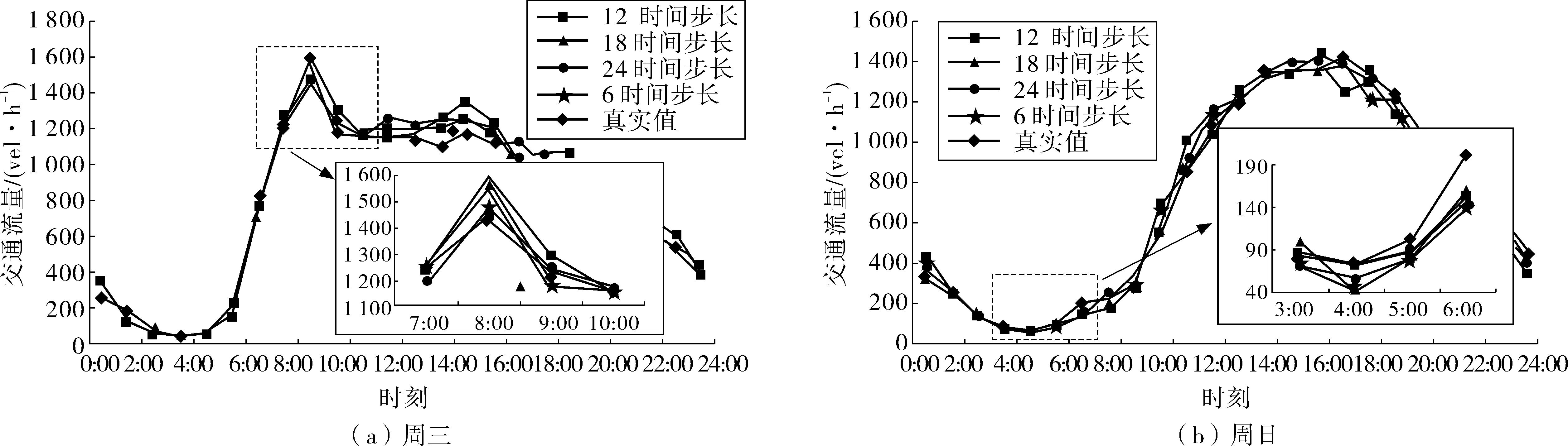
图6 对16-032W观测点周三和周日交通流量的预测比较Fig. 6 Prediction performance comparison for 16-032W in Wednesday and Sunday

5 结 语

笔者提出了基于GRU神经网络的道路交通流量预测方法。GRU神经网络能够挖掘利用时间序列的长期信息，其特征适用于常规交通流量预测问题。为了验证模型的有效性，笔者使用了加拿大大不列颠哥伦比亚省的交通流量数据进行了验证，并与经典的交通流量预测方法ARIMA和SVR进行了对比，最终实验结果表明，该模型在预测交通流量方面其误差和其他预测方法相比有显著降低，如在MAPE评价指标方面，比SVR降低了12.15%，能够有效提高对交通流量预测的准确性。

尽管基于GRU神经网络的模型在道路交通流量预测上取得了不错的效果，但目前笔者只使用了交通流量作为输入数据，并没有将天气状况，交通事故和其他的交通状况(密度或速度)等考虑在内，相信在考虑更多变量后，预测结果会有进一步的提高。另一方面笔者模型主要针对常规交通流量预测，对于非常发性和非重复性的交通流量预测将是未来深化研究的方向。