页岩储层不同渗流形式下的流-固耦合数值模型

李 帅

(西安石油大学石油工程学院， 西安 710065)

地质勘探结果显示，我国具有丰富的页岩油气地质储量和可采储量。页岩储层的孔隙度和渗透率较低，一般需要进行水力压裂而获得贯通的裂缝网络，才具有工业产能。对低渗透、超低渗透储层，须考虑流-固耦合问题。孔隙流体渗流的规律不同，岩石的形变就不同，从而会使岩石的力学性质发生改变，而储层岩石的这种改变又会影响流体的渗流场。储层岩石和流体的这种相互作用，对油气井的生产影响巨大。现以页岩油藏为例，研究建立储层不同渗流形式下的流-固耦合数值模型。

1 页岩储层的流-固耦合模型

储层的流-固耦合描述的是流体和固体之间的相互作用关系。考虑到页岩储层的岩石力学特征和流体渗流特征的复杂性，特做如下假设。

(1) 储层岩石为均质、等厚、可压缩的；

(2) 岩石的变形满足Terzaghi有效应力准则；

(3) 储层变形为弹性力学中的小变形问题，岩石为线弹性材料；

(4) 储层岩石和流体之间不发生物理化学反应，也无组分之间的交换；

(5) 流体在储层之间的渗流为达西渗流；

(6) 岩石的变形会对流体渗流场产生影响，流体的渗流会导致储层的变形和位移；

(7) 不考虑钻井液与井壁之间的水化、蠕变等作用，储层岩石为脆性岩石。

建立如图1所示的极坐标系。

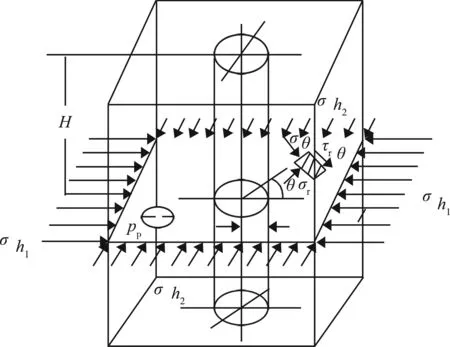
图1 页岩储层钻井示意图

将页岩储层视为弹性无限大地层，则任意一个质点处的变形和位移都可以用平衡方程、几何方程、物理方程来描述。

(1) 几何方程

(1)

式中：εr、εθ、εz、εv—— 分别为研究点距离原点r处的径向应变、周向应变、垂向应变、总应变；

r—— 研究点到原点的距离，m；

u、w—— 分别为质点径向位移、垂向位移，m。

(2) 物理方程

(2)

式中：σr、σθ、σz—— 分别为距离原点r处的径向应力、周向应力、垂向应力，MPa；

λ—— 拉梅常数；

G—— 剪切模量，MPa；

a—— Biot常数；

p—— 孔隙压力，MPa。

(3) 平衡方程

(3)

将式(2)带入式(3)，再将式(1)带入，得到位移形式的平衡方程：

(4)

式中：μ—— 流体黏度，Pa·s。

页岩储层流体的渗流模型用达西定律来描述，其表达式为：

(5)

式中：k—— 储层渗透率，μm2；

K=k/μ。

井眼周围储层流量的表达式为：

(6)

式中：q—— 油井产量，m3/s；

h—— 储层厚度，m。

在极坐标系中，孔隙流体的质量守恒方程(连续性方程)为：

(7)

式中：ρ—— 流体密度，kg/m3；

φ—— 孔隙度。

将式(6)代入式(7)，得到井眼周围储层的渗流数学模型：

(8)

式(4)和式(8)构成储层的流-固耦合方程组。

式(4)反映了储层孔隙压力与研究质点位移之间的关系，式(8)反映的是孔隙压力变化对储层孔隙度的影响。对于储层平面某一个质点，其位移的变化表现为体积的膨胀或收缩，即质点的位移与该点所造成的孔隙度的变化存在数值关系。所以，由式(4)和式(8)组成的方程组，反映了在渗流过程中流体运动与介质变形的相互耦合作用，是一组充分耦合的方程组。

页岩变形的根本原因，是其骨架受到的有效应力发生了变化。根据Terzaghi有效应力原理，岩石骨架所受应力以式(9)表达。

ps=pv-app

(9)

式中：ps—— 岩石骨架所受应力，MPa；

pv—— 岩石所受垂向应力，MPa；

pp—— 岩石孔隙压力，MPa。

储层中质点的位移，可以理解为是质点的形变量ε。由于假设岩石本身是线弹性体，则有：

(10)

式中：E—— 弹性模量，MPa。

因此，当知道储层孔隙压力变化规律及相应的定边界条件和初始条件，便可建立封闭的页岩储层流-固耦合方程[1-3]。

2 不同渗流模型下的流-固耦合模型

(1) 半无限大地层井底压力为定值的不稳定渗流

对于平面一维半无限大带状页岩储层，由渗流力学知，其渗流的孔隙压力表达式如式(11)。

(11)

式(11)(10)(8)(4)和相应的定边界条件及初始条件，就构成封闭的一维不稳定渗流的流-固耦合模型。

(2) 无限大地层中弹性流体向一口井不稳定渗流

页岩储层，在近井地带的流动是径向流。由渗流力学知，其孔隙压力表达式为：

(12)

式(12)(10)(8)(4)和相应的定边界条件及相应的初始条件，就构成封闭的平面不稳定渗流的流-固耦合模型。

(3) 球形不稳定渗流

在页岩储层的钻井过程中，刚钻遇储层时，整个近井地带的流动为球形流，其孔隙压力表达式为：

(13)

式(13)(10)(8)(4)和相应的定边界条件及相应的初始条件，就构成封闭球形不稳定渗流的流-固耦合模型。

上述3种渗流方式下的孔隙压力分布计算模型是最基本的。对于在复杂井网下的页岩储层，可以根据压降叠加原理和势的叠加原理，求得任意一点的孔隙压力数学模型[4]。

3 储层的流-固耦合计算步骤

储层的渗流模式不同，孔隙压力变化规律不同。根据流-固耦合的数值模型可知，孔隙压力的变化会使储层岩石骨架发生形变，而这种形变会导致岩石应力分布发生变化。由此总结储层流-固耦合的计算步骤，如图2所示。

4 结 语

页岩储层的流-固耦合模型对探究孔隙压力变化和岩石形变之间的相互作用关系具有重要意义。本次研究根据弹性力学的基本假设，利用几何方程、物理方程、平衡方程及有效应力准则，得到了页岩储层的流-固耦合模型；根据渗流模型的不同，得到了基本渗流模型下的流-固耦合渗流模型。

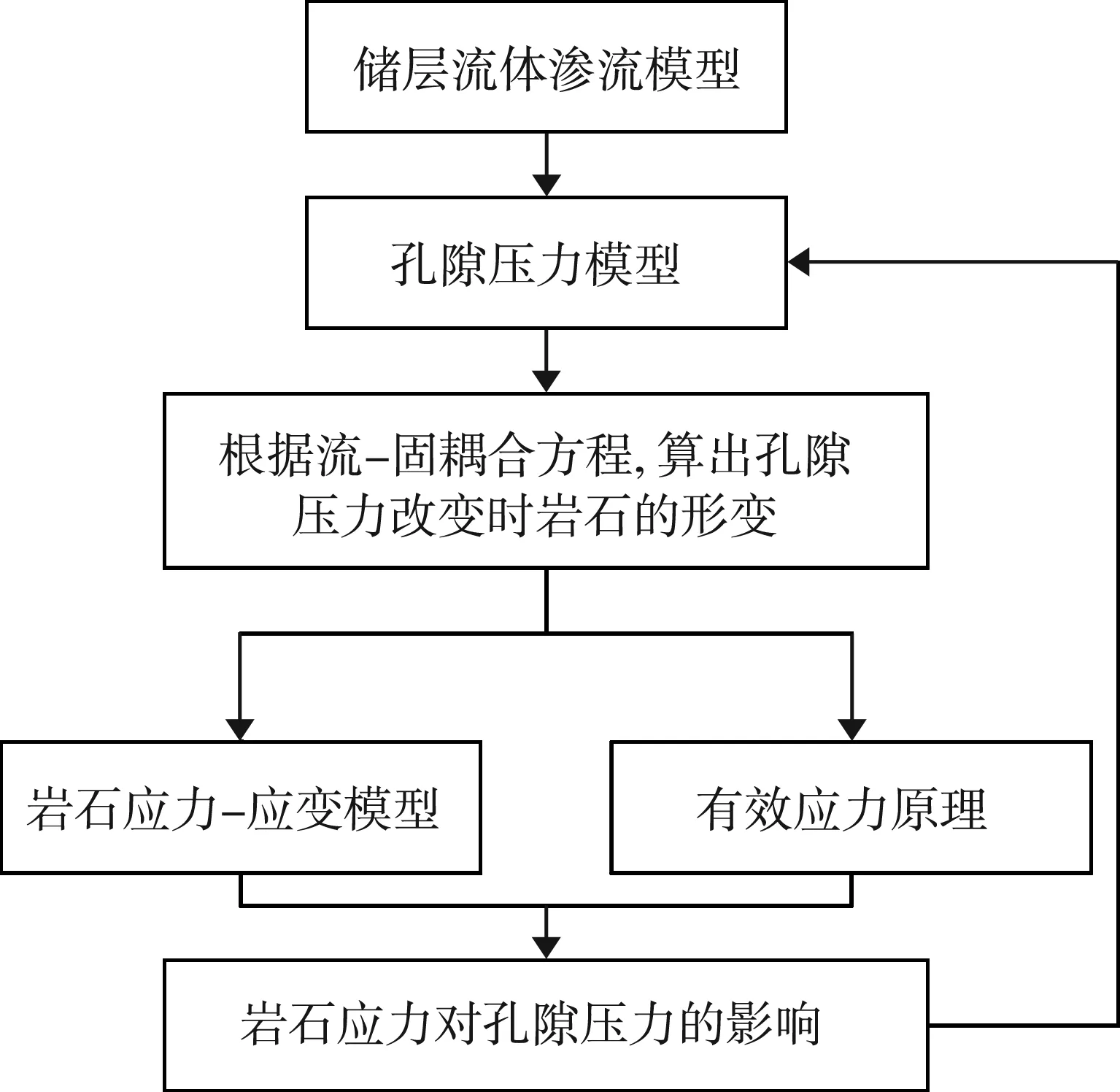
图2 流-固耦合计算模型