对稳态下运动匀质弹簧的研究
涂德新
(江西师范大学附属中学,江西 南昌 330046)
弹簧是物理学中一个重要的力学模型, 绝大多数情况下都是研究轻质弹簧.众所周知:轻质弹簧两端受力必定等大反向,已知其受力则轻质弹簧的长度和弹性势能可以直接求出.轻质弹簧是一个理想化的模型, 真实的弹簧都是有质量的.质量均匀分布的弹簧在生产生活中很常见,有些文献进行了有益的研究[1].本文研究匀质弹簧在平动加速和匀速转动两种情况下达到稳态时的长度和线密度.
1 问题提出

图1
一根质量均匀分布的弹簧,原长为l0,质量为m,劲度系数为k,如图1所示放在光滑的水平地面上.弹簧左端受到向左的拉力F1的作用,右端受到向右的拉力F2的作用,由于两端拉力可能不相等,弹簧整体做加速运动,达到稳定时所有点的加速度与质心的加速度相同,但由于弹簧两端拉力可能不相等,且考虑弹簧有质量,所以弹簧稳定后的线密度一般不均匀.这里求稳态也就是弹簧各部分相对静止时的长度L和线密度分布λ.
2 问题分析
如果考虑弹簧从静止开始的加速过程则弹簧内部各部分之间存在相对振动,问题的求解十分困难.这里求弹簧各部分相对静止时的长度和线密度分布则相对简单.
弹簧两端受力不相等,则弹簧稳态时整体做加速运动,弹簧各处所受的弹力并不相等,于是弹簧各处的形变并不均匀,求解弹簧的长度变得比较困难,不能用胡克定律直接求解.
对弹簧用微元法求解.如图2所示,取弹簧原长x处微元Δx,弹簧达到稳定后此处弹力为Fx,设微元Δx被拉长后的形变量为Δx′,分析出Δx′与Δx的关系,对Δx′进行求和,便可以求得弹簧受力后的总形变量x′,进而求出弹簧的总长度L.
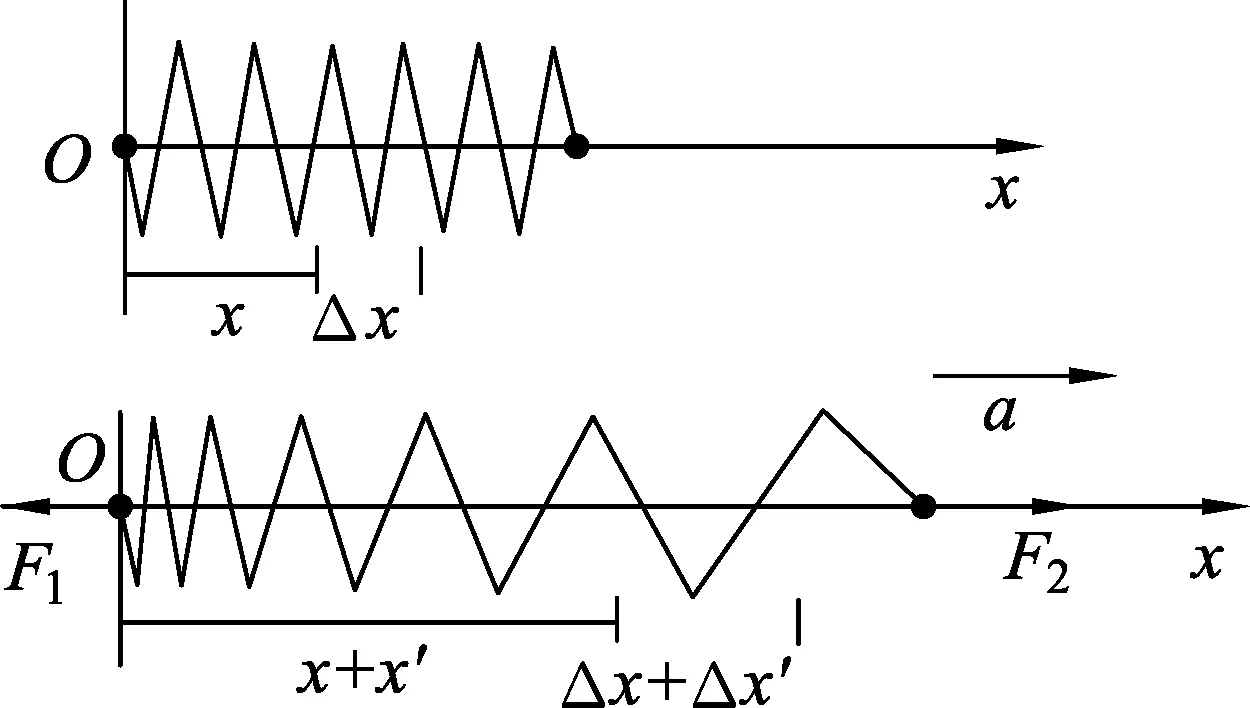
图2
2.1 问题解析
由于弹簧的劲度系数与弹簧的长度成反比[2],总长l0的弹簧劲度系数为k,设原长中微元Δx对应的劲度系数k′,参数间存在关系
k′Δx=kl0.
(1)
微元Δx两端所受的弹力一般不相等,但考虑到微元的质量很小,于是两端弹力的差值也很小,此差值相对两端的弹力属于小量,于是求微元Δx的伸长量时,可以不考虑此差值,认为微元Δx处弹力为Fx,这时对应的伸长量为Δx′,由胡克定律有
Fx=k′Δx′.
(2)
由(1)、(2)两式可得
Δx′=(Fx/kl0)Δx.
(3)
为了求和的方便,不妨将微元改成微分的形式
dx′=(Fx/kl0)dx.
(4)
对弹簧列牛顿第二定律
F2-F1=ma.
(5)
对左端到x处的弹簧列牛顿第二定律
Fx-F1=(x/l0)ma.
(6)
由(5)、(6)两式可得
Fx=(x/l0)(F2-F1)+F1.
(7)
由(4)、(7)两式可得
(8)
将dx′代入可以求得线密度
(9)
又对(8)式积分
求得
x′=(F2+F1)/2k.
(10)
由此求得稳定后弹簧的总长
L=l0+(F2+F1)/2k.
(11)
2.2 分析讨论
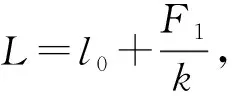
由(9)式, 弹簧的线密度λ是微元位置x的函数.如果F1
3 进阶问题
如图3所示,让弹簧绕过一个端点O的竖直转轴做角速度为ω的匀速圆周运动, 不计一切阻力,不考虑弹簧内部的相对振动,求弹簧各部分相对静止时的长度L和质量线密度分布λ.
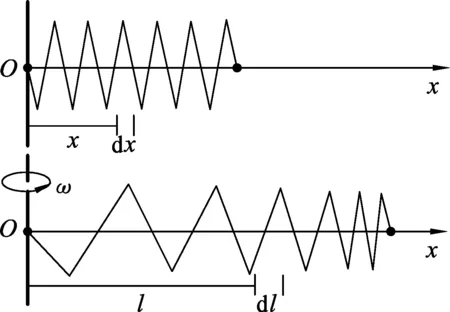
图3
3.1 问题解析
这种情况下弹簧沿长度的形变肯定不均匀,直接对形变后的弹簧不好取微元.采用跟问题一类似的处理方法:设弹簧在原长x处对应伸长后的位置为l=f(x), 两边取微分后有dl=f′(x)dx
3.1.1 求解弹簧长度所满足的微分方程(一)
x处弹簧的弹力Fx充当x到l0处弹簧的向心力

(12)
dx的长度对应伸长后的长度为dl,存在关系
dl=dx+dx′.
(13)
其中伸长量dx′,dx和Fx的关系如(3)式所示.
由(4)、(9)、(10)、(11)式联立求解得
两边对x求导得
3.1.2 求解弹簧长度所满足的微分方程(二)
由(4)、(11)式可得x处弹簧的弹力为
将dl代入有
Fx=kl0[f′(x)-1].
同理
Fx+dx=kl0[f′(x+dx)-1].
x到x+dx处微元受到的合力为
F合=Fx+dx-Fx.
代入后可以改写为
F合=kl0f″(x)dx.
此合力刚好充当微元做匀速圆周运动的向心力
-kl0f″(x)dx=(dx/l0)mf(x)ω2.

3.1.3 求解微分方程
上述方程是二阶常系数线性齐次微分方程.由微分方程理论可知,该方程存在通解
考虑到稳定后的边界条件:对于固定端f(0)=0;而自由端微元的长度并没发生形变,微元的相对长度f′(l0)=1.由边界条件可以求解得

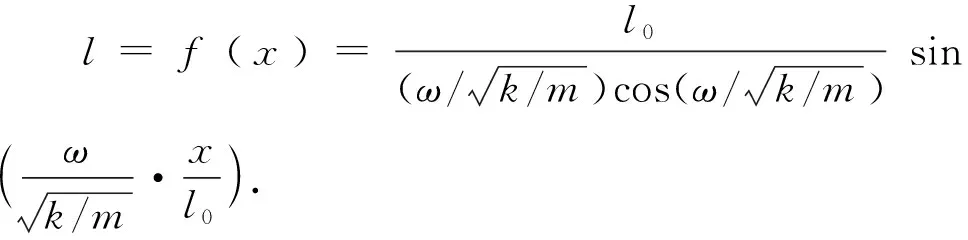

再求稳定后弹簧的线密度λ.
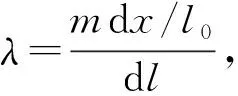
代入可以求得
3.2 分析讨论
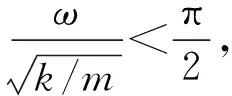
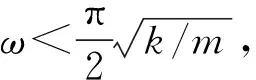
4 后记
本文在处理弹匀质弹簧问题时, 考虑到伸长后的弹簧形变不均匀, 不好取微元, 于是先假设弹簧形变后的函数, 再分析形变后的微元与形变前的微元的对应关系, 并对形变前的微元进行积分, 进而对匀质弹簧问题得到了比较简洁的处理. 希望这种特殊的处理方法对各位同仁有所借鉴.

