A one-dimensional transport model for multi-component solute in saturated soil

Zhi-hong Zhang*,Jia-pei Zhang,Zhan-ying Ju,Min Zhu

Key Laboratory of Urban Security and Disaster Engineering of Ministry of Education,Beijing University of Technology,Beijing 100124,China

Abstract A modified multi-component solute diffusion equation described with diffusion flux was derived in detail based on the classical Maxwell-Stefan diffusion theory.The friction between the solute species and the soil skeleton wall,which is proportional to the relative velocity between the solute species and the soil skeleton,is introduced.The chemical potential gradient is considered the driving force.A one-dimensional model for transport of multi-component solute in saturated soil was developed based on the modified diffusion equation and the modified competitive Langmuir adsorption equation.Numerical calculation of a case of two heavy metal ion species,which was chosen as an example,was carried out using the finite element software COMSOL Multiphysics.A comparative analysis was performed between the multi-component solute transport model developed in this study and the convection-diffusion transport model of single-component solute based on Fick's law.Simulation results show that the transport behavior of each species in a multi-component solute system is different from that in a single-component system,and the friction characteristics considered in the developed model contribute to obstructing the movement of each solute component.At the same time,the influence of modified competitive Langmuir adsorption on solute transport was investigated.These research results can provide strong theoretical support for the design of antifouling barriers in landfills and the maintenance of operation stability.

©2018 Hohai University.Production and hosting by Elsevier B.V.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

Keywords:Multi-component solute;Maxwell-Stefan diffusion;Competitive adsorption;Friction;Transport

1.Introduction

It is of paramount importance to describe the multicomponent solute transport behavior reasonably and accurately for geoenvironmental projects in operation.The characteristics of multi-component mixtures,such as the leachates in waste landfills or dredged sediment,are significant to the process of solute transport.When a multi-component mixture enters a porous medium,physical,chemical,and biological interactions will occur between solute species and between the solute components and the porous skeleton,which can influence the solute concentration distribution.

A large amount of research has been conducted on multicomponent solute transport problems,including experimental studies,theoretical analysis,and numerical simulation.The competitive adsorption mechanisms of multi-component heavy metal ions in soil have been determined through experimental investigation(Liu et al.,2014;Zhang et al.,2007;Wang et al.,2006).The results have indicated that the soil has properties of selective adsorption for multi-component heavy metal ions,and,compared with the adsorption of single component heavy metal ions,the adsorption capacity of soil for each heavy metal component decreases to different extents.The competitive adsorption model of multi-component solutes(Markham and Benton,1931;LeVan and Vermeulen,1981;Jain and Snoeyink,1973),multi-component gas diffusion model(Runstedtler,2006),and a variety of charged particle diffusion models(Muniruzzaman et al.,2014)have been established and used for theoretical analyses of competitive adsorption properties of multi-component solute ions,diffusion characteristics of multi-component gas,and diffusion characteristics of multiple charged particles,respectively.With regard to numerical simulation,an alternative diffusion and transport model of multi-component gas diffusion and flow in bulk coals has been presented(Wei et al.,2007),and the multicomponent gas diffusion has been stimulated with the friction produced by gas molecular collisions against the pore walls(Krishna and Wesselingh,1997).The diffusion behavior of multi-component gas in porous media has been simulated successfully,forming the foundation of multi-component gas diffusion theory.

The aforementioned research contributes to an understanding of the problem of multi-component solute transfer in porous media.Nevertheless,most of the investigations have been limited to the multi-component gas diffusion problems.The phenomenon of multi-component solute transport in porous media has not been studied in depth.The purpose of this study was,therefore,to establish a one-dimensional multicomponent solute transport model in saturated soil based on multi-component solute competitive adsorption and diffusion mechanisms.In the model,the friction between the solute species and the soil skeleton wall,which is proportional to the relative velocity between the solute species and the soil skeleton,was introduced and the chemical potential gradient was considered the driving force.Numerical calculation was carried out using the finite element software COMSOL Multiphysics,with the case of two heavy metal ion species chosen as a simple example.The differences between the single component and multi-component solute convection-diffusion transport models were analyzed.The usability and rationality of the established multi-component solute transport model are discussed in detail.

2.Basic theory of solute transport

2.1.Adsorption equations

Adsorption is one of the main mechanisms of solute transport.Three kinds of competitive adsorption equations,the competitive Langmuir(CL)adsorption equation(Eq.(1))(Zhang et al.,2007;Markham and Benton,1931;Xi,2001),the LeVan-Vermeulen adsorption equation(LeVan and Vermeulen,1981),and the modified competitive Langmuir(MCL)adsorption equation(Eq.(3))(Jain and Snoeyink,1973;Broughton,1948;Banerjee et al.,2013)have been used to describe multi-component transient adsorption performance.

To obtain the actual adsorption behavior,the assumptions of the CL equation and the MCL equation are based on the Langmuir equation for single-component solutes.The three assumptions are as follows:(1)the surface of adsorbent is uniform;(2)the adsorbent is capable of adsorbing only a single layer of solute ions;and(3)there is no interaction between the adsorbed solute ions.

The CL equation is as follows:

where qiis the amount of solute component i adsorbed per unit weight of adsorbent at equilibrium concentrations,qimis the maximum amount of the adsorbed component i,m is the number of components,kiis the partition coefficient of solute component i,and ciis the equilibrium concentration of component i in the solution.

The following comparison expression can be obtained based on Eq.(1):

Eq.(2)means that the adsorption capacity of component i in the CL equation is less than that in the Langmuir equation for a single component,so the competition between components can be embodied through the CL equation.

The MCL equation is as follows:

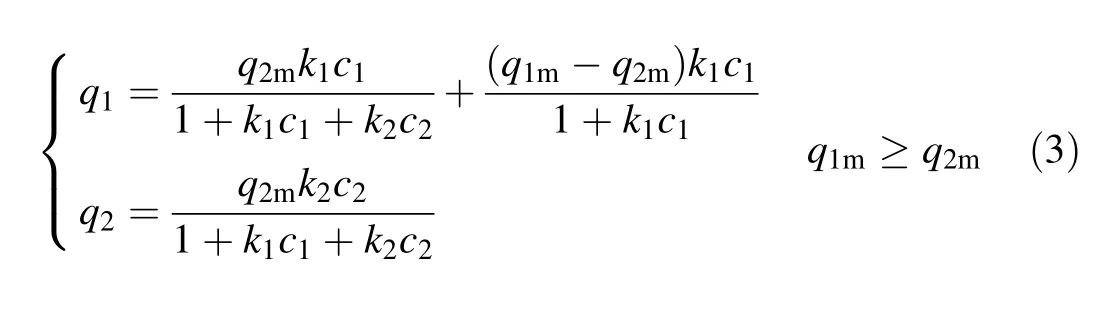
The adsorption surface is assumed to be divided into two parts in the MCL equation.The first part of the surface adsorbs all kinds of species,and the second part of the surface only adsorbs the species with maximum adsorption capacities.Thus,for species with maximum adsorption capacity in the MCL equation,the adsorption amount equation is a combination of the CL equation for species with a small adsorption amount and the Langmuir equation for single species with an adsorption amount difference.Therefore,there exists a larger adsorption amount for components with maximum adsorption capacity using the MCL equation than for those using the CL equation,so the competitive interactions among components can be expressed in view of the adsorption capacity.In conclusion,to a certain extent the MCL equation has overcome the irrationality of parameter values of the CL equation.In this study the MCL equation was adopted.

2.2.Diffusion in multi-component system

The mass transfer theory is based on Fick's law.However,there are deficiencies in Fick's law when considering multicomponent coexistence and various driving forces.In the 19th century,Maxwell and Stefan conducted a lot of work on the kinetic theory of gases based on previous research.Further study on multi-component mass transfer problems has been performed by Krishna(1987a,1987b,1987c).The Maxwell-Stefan equation,which is a more accurate equation than that of Fick's law,is based on the momentum balance of each component in the mixture:

where Fidenotes the driving force(potential gradient)of diffusion of component i,which includes the concentration gradient,electric potential gradient,pressure gradient,centrifugal field gradient,temperature gradient,and so on;ζijis the friction coefficient between components i and j;xjis the mole fraction of component j;and uiand ujare the diffusion velocities of components i and j,respectively.

The chemical potential of component i,μi,can be expressed by the following equation:

where μ0is the initial chemical potential,P is the pressure,R is the universal gas constant,T is the temperature,γiis the activity coefficient of component i,and xiis the mole fraction of component i.

Substituting the equation Fi=-dμi/dz into Eq.(4)when the driving force of diffusion only involves chemical potential,and describing the diffusion flux with Ni=ciuiand Nj=cjuj,the generalization for multi-component mixtures is obtained:

where Dijis the diffusion coefficient,and Dij=RT/ζij;z is the depth;and c is the sum of concentrations of all species in the equilibrium solution.Eq.(6)is known as the classical Maxwell-Stefan diffusion equation (Taylor and Krishna,1993).

For mass transfer of a multi-component gas mixture in porous media,the dusty-gas model has been developed(Krishna and Wesselingh,1997),in which the friction produced by collision between gas molecules and the pore wall is considered.It can be expressed in the following form:

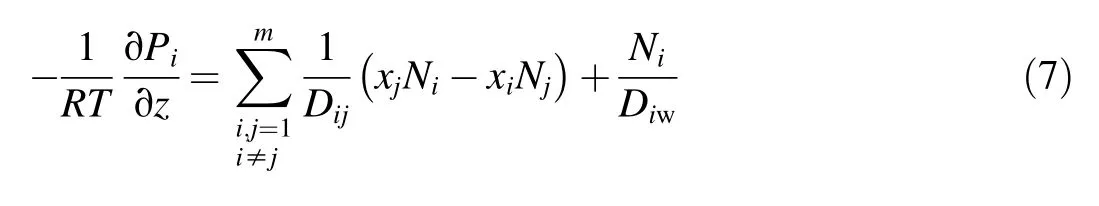
where Diwis the diffusion coefficient of gas component i;Piis the pressure of gas component i; and Diw=with dpbeing the radius of the porous medium and Mibeing the molar mass of component i.A conclusion can be drawn that when the mean free path of a gas molecule is greater than the diameter of porous media,the gas molecule can collide with the pore walls(Krishna and Wesselingh,1997;Cruz et al.,2006).This type of mechanism is defined as the Knudsen diffusion.

In this study the key issue was the diffusion of multicomponent solutes in porous media.The friction caused by the collision of solute molecules against the pore wall was introduced based on Eq.(6),when the aperture of porous media was less than the mean free path of solute molecular diffusion.Meanwhile,the following assumptions were employed for multi-component solute diffusion in porous media:(1)the skeleton of the porous medium was assumed to be continuous and rigid;(2)the friction between components and the pore wall was proportional to the relative velocity of components and the pore skeleton;(3)the diffusion driving force of components only included the chemical potential gradient;and(4)the diffusion process was isothermal.

According to these assumptions a diffusion equation(Eq.(8))for multi-component solute in dense soil(clay)was established on the basis of Eq.(6),in which two kinds of friction were considered in the multi-component solute diffusion process:the friction between components,and the friction between components and the pore wall.In addition,mechanical equilibrium was adopted so that the diffusion driving force was equal to friction.Eq.(8)provides the relationship between the diffusion driving force and friction:

where ζiwis the coefficient of friction between specie i and the skeleton(pore wall),which is related to many factors such as solute molecular properties,temperature,material properties of porous media,arrangement of particles in porous media,surface roughness of the skeleton,and the void tortuosity of porous media.

Substituting the equation of the diffusion driving force Fi=-dμi/dz into Eq.(8),the following formula can be obtained:

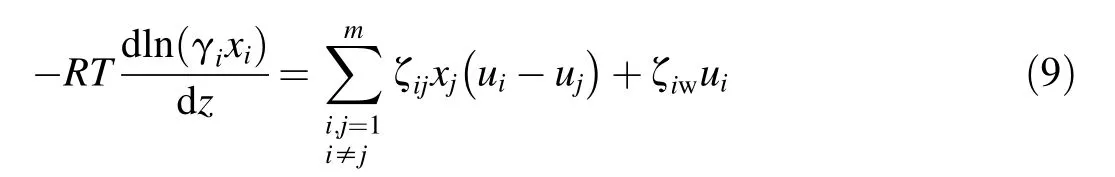
Both sides of Eq.(9)are multiplied by xi,leading to

Letting Dij=RT/ζijand Diw=RT/ζiw,the diffusion fluxes of species are expressed by Ni=ciuiand Nj=cjuj,which are substituted into Eq.(8),which can then be expressed as

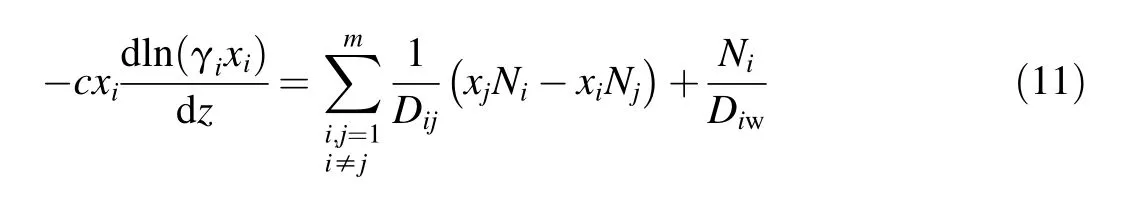
where the activity coefficient of component i is in accordance with the formulas:γi= γi（T，P，x1，x2，…，xm-1）(Cruz et al.,2006)and γi=1 for the ideal solution (Krishna and Wesselingh,1997).Each component has a diffusion equation like Eq.(11)for a mixture containing m kinds of components,so an equation system including m equations is produced.Then,the diffusion flux can be obtained through solution of the equation system as follows:

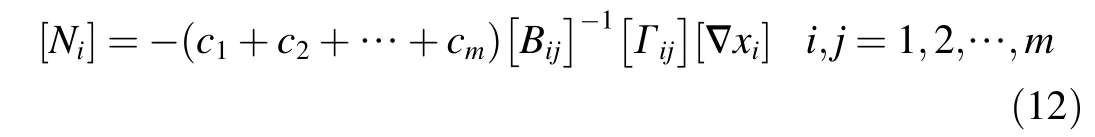
Here,the following formulas are adopted:

2.3.Transport model of multi-component solute

According to the law of conservation of mass,a one dimensional transport model of solute in saturated soil was established,in which the MCL equation was used,the diffusion considers the friction between species and the friction between species and the pore wall,and the convection was also taken into account.Here,for the sake of simplicity,the case of two species is chosen as an example.The developed one-dimensional two-component solute transport model using the MCL equation(hereafter referred to as the two-component MCL model)is expressed in Eq.(13):

where n is the porosity,ρsis the density of the soil skeleton,and v is the convection velocity.

An equation system including two equations is produced:

Here,the following formulas are adopted:

3.Numerical simulations

3.1.Model parameters

Using the case of two heavy metal components Cu2+and Ni2+as an example,the values of model parameters are listed in Table 1.

The friction coefficient of species is satisfied with ζij= ζjiaccording to the results of other researchers(Datta and Vilekar,2010;Maxwell,1867).Because Dij=RT/ζij,Dij=Dji,i.e.,the diffusion coefficient Dijis the same for Cu2+and Ni2+.

According to the assumption that the friction between Cu2+and the pore wall is larger than the friction between Ni2+and the pore wall,the diffusion coefficient Diwof Cu2+is less than that of Ni2+.The solution is assumed to be ideal.That is,the value of the activity coefficient is taken to be 1.

3.2.Simulation results and analysis

The source concentrations of Cu2+and Ni2+were kept constant in this simulation,the initial boundary concentrations of the two species were both 4 mol/m3,the transport depth simulated was 2 m,the density of soil was 2.72 g/cm3,and the porosity was 0.44.The numerical simulation was conducted using the finite element software COMSOL Multiphysics,and the partial differential equation(PDE)module was used.

The transport of solute was simulated with the two component MCL model and the nonlinear Langmuirconvection-diffusion model for a single-component solute(hereafter referred to as the single-component Langmuir model).The simulation results are shown in Figs.1 and 2.

Table 1 Model parameters of solute transport for two components with MCL model.

From the results of solute concentration distribution with depth at different times shown in Fig.1,it can be determined that the transport velocity of Cu2+is slower than that of Ni2+as calculated by the multi-component solute transport model developed in this study.Furthermore,it is worth noting that the transport velocities of Cu2+and Ni2+obtained with the multi-component solute transport model are slower than those obtained with the single-component Langmuir model.The reasons are that the friction between Cu2+and the soil skeleton is greater than the friction between Ni2+and the soil skeleton for the multi-component solute transport model,and the single-component Langmuir model includes a modified competitive adsorption mechanism,in which there is a stronger adsorption capacity for Cu2+than for Ni2+.In other words,the friction both between species and between species and the soil skeleton in the developed multi-component solute transport model has significant effects on solute transport,in that it slows down the solute transport simulated by the single-component Langmuir model,and the lag increases with transport time.In conclusion,the developed model can decrease the effective depth of barriers,which is beneficial to the design of landfills.

The results of solute concentration distribution with time at different depths shown in Fig.2 demonstrate that,at the same depth,the transport time that it takes Cu2+to reach the same concentration is longer than that of Ni2+calculated by the two-component MCL model.Furthermore,the transport times of Cu2+and Ni2+in particular,which are obtained with the two-component MCL model,are longer than those obtained from the single-component Langmuir model.The lag is greater with the increase of soil depth.

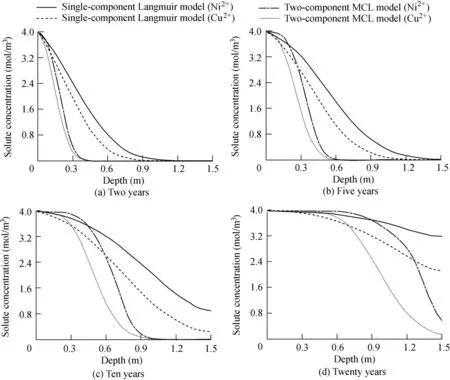
Fig.1.Solute concentration distribution with depth at different times.

Fig.2.Solute concentration distribution with time at different depths.

4.Conclusions

A one-dimensional transport model for multi-component solute in saturated soil was developed based on the Maxwell-Stefan diffusion theory and the MCL equation.Numerical simulations were conducted with the finite element software COMSOL Multiphysics,and the case of two heavy metal ion species was chosen as an example.The following conclusions can be drawn:

(1)The modified multi-component solute transport model in porous media has a clearer physical meaning than the empirical Fick's law,and can thoroughly explain the diffusion process of multi-component solute using the friction mechanism.

(2)Friction has obstructive effects on multi-component solute transport according to comparative analysis of simulation results,providing a theoretical foundation for the design of antifouling barriers in many geoenvironmental fields.

(3)The transport velocities obtained from the two component MCL model are much slower than those from the single-component Langmuir model.Therefore,the thickness of the impervious layer or antifouling barrier can effectively decrease,which will greatly reduce construction costs.In the future,the one-dimensional model developed in this study will be extended to three dimensions.