基于上海地区货物配送带时间窗VRP问题研究

赵吉祥，姚兴贵，孟初夏

（安徽农业大学 工学院，安徽 合肥 230036）

某轮胎供应商负责上海地区货物的运输安排，需要在一天之内按订单要求的配送量和运送时间送到客户手中.综合考虑客户订单数量，具体位置、运送时间和配送量以及时间窗等限制条件进行合理地求解货物配送方案.

1 合理优化路线模型的建立与求解

所有156个客户点的位置坐标，每两个客户点之间的距离包括任意一点到仓库的距离，每个客户点的订单数及收货时间，配送车辆载重及工作时间等数据均为已知.156个客户点数据相对较大，而且较为分散，如果采用直接对其分析最优路线较难实现，所以考虑需要先将整个区域划分为几个小的区域，然后再对分出的小区域进行逐一优化内部线路，得出一个完整的配送方案.

首先应用k-means聚类分析[1]对客户点进行聚类划分，将大规模的VRPTW问题简化成小规模的VRPTW问题，然后再对每一个小的VRPTW问题结合货车的承载能力对其内部建立优化方案，使用模拟退火算法对各个小区域进行优化，通过MATLAB编程，有效地实现了对区域内路径的自动寻优，建立了一套合理的优化配送模型.

在两种不同配送车型情况下，容量为qv的车辆，现有L项货物运输任务，以1，2，…，l56表示，已知任务i的货运量为pi（i=1，…，l），且0≤pi≤qv,qmax为最大车型容量，qmin为最小车型容量，m为所需的车辆数.由于事先难以确定用车的数量，所以用下列公式得出用车的大概范围[5]:

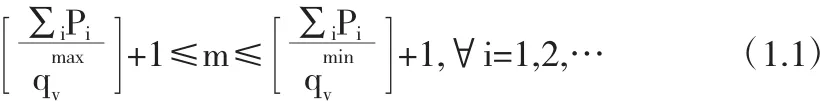
然后在算法中取合适的可能值，结合题目中数据最大容量为150，最小容量为75，所有客户总的需求量为642，算出用车的大概范围为6≤m≤9.首先取m=6,即将整体区域划分为6个区域，通过软件求解对156个点进行聚类划分，得六个区域所包含的客户点分布.

对所有点进行聚类划分之后使用模拟退火算法对各个区域进行内部优化.本篇文章在林郁丞、李军、郎茂祥、张潜等[1-4]研究的基础上，充分考虑问题的约束条件和优化目标，建立以下所述目标函数：

其中v表示第v辆车，N表示总的送货量，Pv表示第v辆车的载重量，Gv表示由车辆v服务客户的集合，Si表示车辆在客户的服务时间,tij表示车辆从客户i到客户j所花费的时间，Tvo表示车辆v的开始工作时间,Tkv表示车辆v的结束工作时间,下同.

通过Matlab编程模拟退火算法，根据各种限制条件求得各个区域的最优配送路线.

2 考虑交通影响的合理配送路线模型的建立与求解

现实运输中需要考虑到实际交通情况，有可能会出现拥堵现象，导致问题一天中在理想情况下得出的优化路线并不能满足实际情况下的配送要求.

通过从百度地图上查找的上海市交通路线图及不同时段的交通通行能力可知，上海市在一天中的堵车高峰时间一般在早晨8-9点.考虑道路拥挤程度对配送的影响，引入交通工程学中的道路阻抗系数λij[1]进而建立了带时间窗车辆问题的数学模型，应用两阶段启发式算法求解.

首先，仍采用模型一的算法，先确定使用汽车的数量范围，使用（公式1.1）进行计算，在算法中取合适的可能值.结合题目中数据最大容量的为150，最小容量为75，所有客户总的需求量为642，算出用车的大概范围为6≤m≤9.仍先取m=6，即6辆车，通过软件求解对156个点进行聚类划分，得6个区域.考虑道路拥挤程度对配送的影响，引入交通工程学中的道路阻抗系数[1]

其中，qij表示单位时间内路段实际可通过的车辆数；α、β为阻滞系数，其中α、β的取值分别为α=0.15，β=4[1].对所有点进行聚类划分之后使用模拟退火算法对各个区域进行内部优化,建立目标函数如下所示：

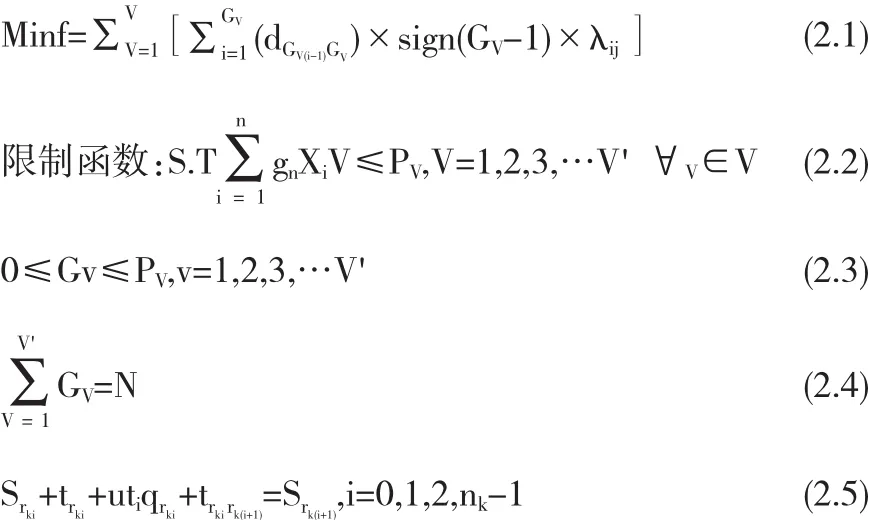
通过MATLAB编程模拟退火算法，综合时间窗，汽车载重及配送线路距离要求求得各个区域的最优路线，得到合理配送方案结果.

3 模型的评价与推广

对于通过公式求得的车辆数的使用范围，本篇文章均取m的最小值，因为从客户点的分布情况来看，存在一部分较分散的点，这些点之间的距离较大，而使用k-means算法以距离为依据对其进行聚类划分时即使增加划分的区域也不可避免距离较大的点划分为一类的数目仍然较少，所以首先取最少的车辆即划分区域，然后对局部总载重量超过汽车容量及一辆车无法按照客户要求时间送到的区域，进行适当的增派车辆.

由于k-means算法的众多局限性，可以考虑将它与全局搜索法结合起来用于聚类分析中.对于模拟退火算法，可以在基本算法的基础上与其他算法结合，以便对问题求解更加便捷、准确.