基于Bootstrap抽样的水文干旱不确定性分析——以北洛河为例

王文川，韩东阳，马明卫，2

(1.华北水利水电大学水利学院，河南 郑州 450046；2.河海大学水文水资源与水利工程科学国家重点实验室，江苏 南京 210098)

干旱作为全球最为常见的自然灾害之一，已经对人类的生存环境造成了严重的影响。土地荒漠化进程加剧、生态系统日渐脆弱、水资源短缺等问题都是干旱的重要表现。目前，研究中较常涉及的干旱类型包括气象干旱、农业干旱和水文干旱。气象干旱大多以降水量作为指标，土壤含水量通常作为衡量农业干旱的重要依据，而水文干旱的主要表现则是河川径流量持续偏少。据测算，全球不同地区每年因干旱造成的经济损失高达60亿～80亿美元，已成为最严重的气象灾害之一[1]。国内外众多学者对干旱和干旱指标做了大量研究，但由于地理位置差异，气象条件不同以及人类活动的影响，干旱指标往往差异很大。正因如此，诸如降水Z指数，降水距平百分率，标准化降水指数(Standardized Precipitation Index，SPI)，标准化流量指数(Standardized Flow Index，SFI)，帕尔默干旱强度指数PDSI等一系列干旱指标先后被提出和应用。其中，标准化流量指数SFI采用Γ分布概率来描述径流量的变化，其计算过程简单，能较好地反映不同时段的水文干旱状况。本文选取SFI指数作为干旱分析指标，基于渭河流域交口河水文站1952—2016年的逐月实测径流系列定量评估北洛河的历史水文干旱演变特征。研究结果能够揭示研究区河川径流丰枯变化的概率统计特性，对监控区域水文干旱情势以及应对干旱的水资源配置具有现实意义。

1 基于Bootstrap方法的标准化流量指数计算原理

Boostrap方法是一种增广样本的统计推断方法，最早由美国斯坦福大学Efron[2]教授提出。经过几十年的发展，这种统计推断方法已被应用到各种领域[3- 5]，以Bootstrap为主题的研究及应用成果不计其数[6- 7]。现对Bootstrap方法的基本原理简单描述如下：

假设给定的观察样本便是总体，总体的分布是未知的。在总体中随机有放回的抽取样本，由此得到的新样本称为自助样本。通过对总体的重复采样，对每一个自助样本计算均值、方差等参数的估计值，根据相应估计参数的分布直方图，就可得到由Bootstrap方法估计参数的经验分布，一般假设为正态分布[8]。利用这些信息估计总体的分布参数，从而获得观察样本的分布函数统计参数，并计算出相应的均值，方差等估计参数。

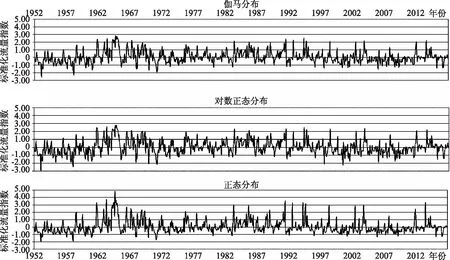
图1 1952—2016不同分布函数SFI时序分布图

Bootstrap的优点在于仅基于观测样本进行再抽样，不需要对总体分布进行假设。借助Bootstrap抽样，可以定量估算由于数据长度限制可能引起的分布参数估计的不确定性。

基于Bootstrap抽样的标准化流量指数SFI具体计算步骤如下[9]：

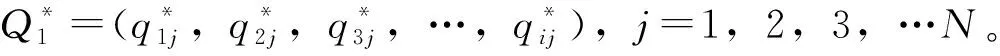
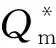
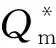
(5)将分布函数F标准正态化，得到某年的SFI。具体计算步骤见参考文献[10]。

此外，本文分别采用标准Bootstrap、百分位数Bootstrap、t百分位数Bootstrap三种抽样方法进行比较分析，其核心思想都是通过对样本重复随机抽样获得再生样本，分别求得标准正态分布下、百分位数下、t百分位数下再生样本均值的置信区间。具体计算步骤见参考文献[11]。以期在假设流量序列服从伽马分布下利用Bootstrap方法估计形状参数α和尺度参数β。以更好的控制分布线型形状，提高标准化流量指数的计算精度。

2 基于Bootstrap方法的标准化流量指数实例应用

2.1 研究区概况

北洛河是渭河最大的支流，黄河二级支流，也是陕西省内最长的河流。交口河水文站建于1952年，是北洛河中游干流控制站，位于洛川县交口河镇，地处东经109°21’，北纬35°39’，集水面积17180km2，属于大陆性季风气候，春季秋季雨少干旱，夏季多暴雨雷雨天气，为年内的主要降雨时段。因此，该地区干旱与洪涝交替的特征显著。

2.2 概率分布线型不确定性分析

标准化流量指数(SFI)的计算核心是将流量序列用以合适的概率分布函数进行拟合。采用不同的概率分布函数拟合流量序列可得到不同的SFI值，本文采用伽马分布，对数正态分布，正态分布三种分布函数分别拟合流量序列得到不同分布的SFI值。以伽马分布拟合计算得到的SFI值为例，与另外两种分布拟合结果进行对比分析，做SFI时序分布图，如图1所示。结果显示，伽马分布和对数正态分布在Bootstrap抽样中得到的SFI值基本趋于一致，且在旱涝趋势识别上结果呈现较高的一致性。基于正态分布计算的SFI存在汛期高估，非汛期低估的现象。导致这样的结果可能是由于分布线型的不确定性引起的。伽马分布和正态分布计算的SFI值更接近合理范围。本文使用伽马分布计算SFI。

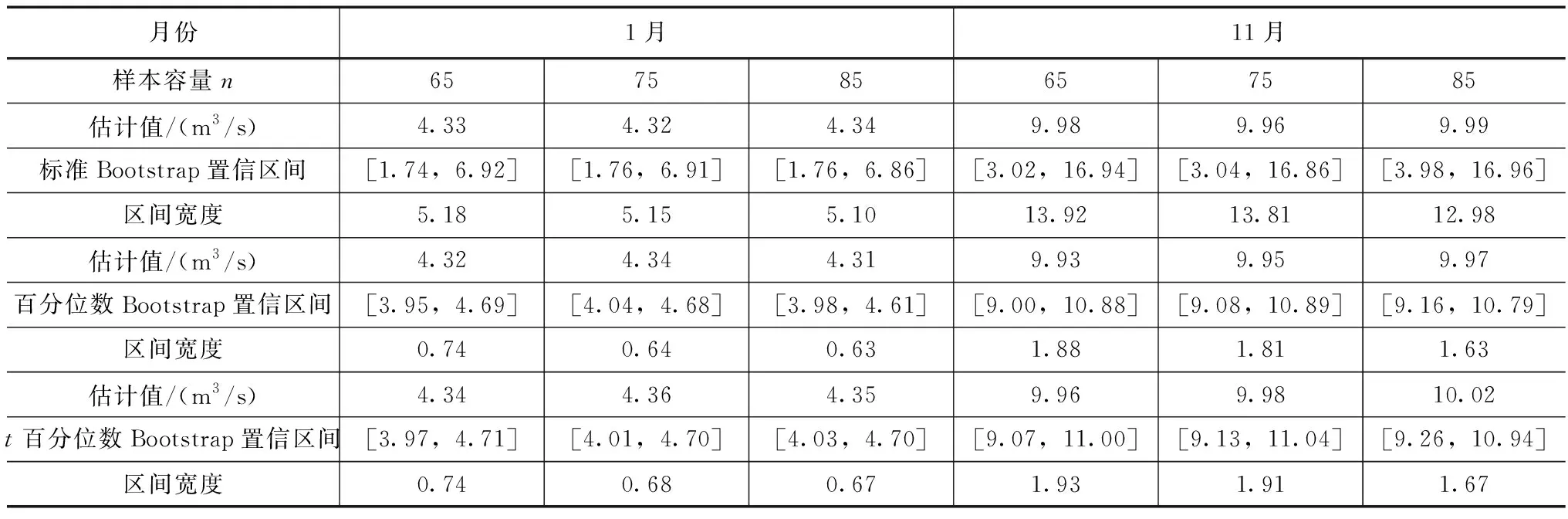
表1 交口河水文站1月和11月流量期望值Bootstrap区间估计

2.3 估计参数不确定性分析

选取渭河流域北洛河中游干流控制站交口河水文站65a(1952—2016年)的实测逐月流量资料为样本。以1月和11月的流量系列为例，对每一个月流量系列抽取N=1000个Bootstrap样本，对每一个Bootstrap再生样本，分别取样本容量n=65、75、85。分别采用标准Bootstrap方法、百分位数Bootstrap方法、t百分位数Bootstrap方法估算流量期望值5%置信水平下的置信区间[12]，区间宽度越大，抽样不确定性也越大[13]。计算结果见表1。

比较分析三种方法计算出来的区间宽度，在样本容量n相同的情况下，利用百分位数Bootstrap方法较其他两种方法计算结果区间宽度最小，精度最高。标准Bootstrap方法计算出来的区间宽度最大，表明其抽样的不确定性大。对同一个月流量系列，样本容量增大，区间宽度呈减小趋势。由此可得，利用百分位数Bootstrap方法进行抽样分析，其计算结果较其他两种方法更好一些，抽样不确定性更小一些，由此方法估计均值、方差等参数的准确度更高。因此，推荐使用百分位数Bootstrap方法估计样本的均值、方差。假设样本流量序列服从伽马分布[14]，由估计出的样本均值和方差反推伽马分布的状参数α和尺度参数β。由此计算标准化流量指数，可以减小抽样方法对计算标准化流量指数的不确定性。

2.4 水文干旱不确定性分析

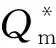
表2 SFI干旱等级划分标准

对交口河水文站65年流量资料进行SFI计算，划分干旱等级。计算结果如图2所示。自1952年建站以来到2016年，交口河水文站控制的区域干旱多发生于1—2月。其中1953年发生连续4个月的持续性干旱，随后仅在1958年的1月2月和1961年的1月发生短期严重干旱，其余时间里鲜有重旱发生。1977年到2016年40年时间里，交口河水文站控制的区域整体是趋于无旱的。仅2005年12月，SFI值为-1.54，划分为重旱等级，但于下年1月2月河道流量逐渐增大，及时补充水资源量，干旱程度有所缓解。在非汛期，偶尔会有流量偏小情况，但持续时间短，对下游影响较小，可忽略其干旱影响。

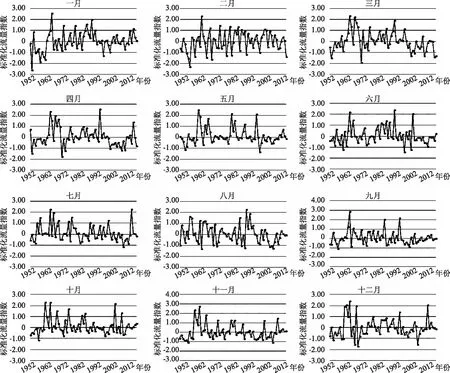
图2 1952—2016年不同月份SFI时序分布图

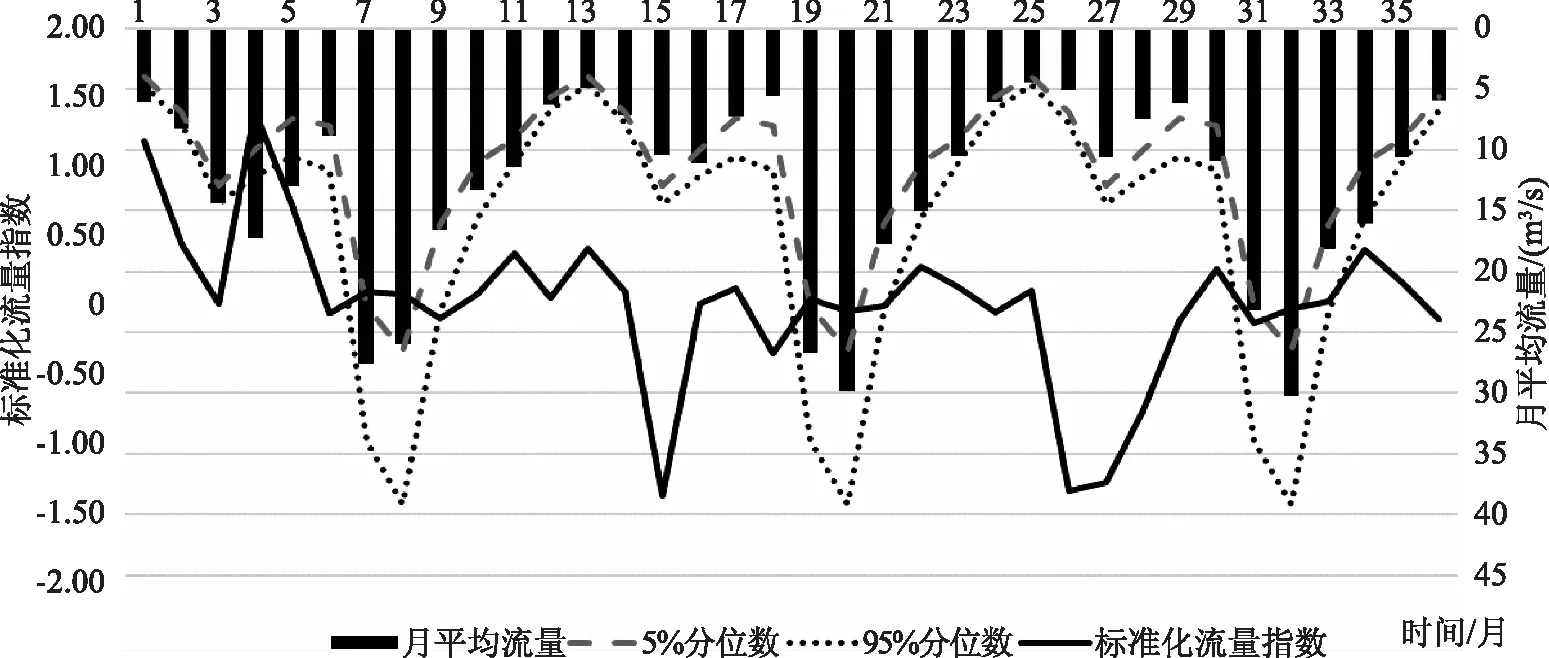
图3 2014—2016年SFI时序分布图

以2014—2016年为例，选用95%置信度下流量序列Bootstrap样本均值的不确定性范围，即以再抽样样本均值排序的2.5%和97.5%两个分位点的区间数值作为月平均流量的不确定性范围，如图3所示。由图3可得不确定性范围的大小与月平均流量密切相关，月平均流量越大，不确定性范围越大，不确定性范围小的地方流量也越小。图中有21个观测值都在不确定性范围内，占所有观测值的58.3%，计算结果属可接受范围。但并不是所有的观测值都在不确定范围内，表明标准化流量指数不能完全的表示出控制区域的干旱程度。这一方面与研究区域的天然河道流量不确定性有一定关系，即同一月份不同年份的月平均流量可能相差很大。另一方面，伽马分布线型也会对标准化流量指数的计算结果有一定的影响，形状参数α和尺度参数β的估计值间接影响着干旱等级的评定。

3 结论与建议

Bootstrap方法可以在总体分布未知的情况下，以有限的样本通过有放回的抽样，定量计算由数据长度的限制引起的抽样不确定性，发现数据长度越长，抽样不确定性越小。以标准Bootstrap、百分位数Bootstrap、t百分位数Bootstrap方法估计流量期望值得置信区间，定量评价了抽样方法的不确定性。区间宽度越窄，对SFI的估计越稳定。

由于影响水文干旱的因素众多，本次研究只考虑流量因素，气候因素和人类活动等因素都未考虑在内，对于干旱评估比较单一。序列的非平稳性以及不同时间尺度的滑动月平均流量累积序列都有可能影响SFI的不确定性，这些问题都有待进一步研究。