时间加权的h指数研究

郭 强，赵 瑾（．郑州大学信息管理学院；．中国人民解放军炮兵学院军事运筹教研室）

1 直观认识

h指数与作者的影响力具有较好的相关性，所以能够利用h指数来对作者的影响力进行衡量。［1］需要指出的是，由于传统的h指数是一个累积量，某一领域过去的高影响力作者和现在的高影响力作者会具有相同的h指数，这样需要将这两种情形区分开来，特别是能否只通过h指数来对这两种类型的作者进行识别。在这里构造这样的h指数，使其具有对距离考察时间越近的作者影响力越注重的性质，或者说对作者越近期的影响力越注重，而对于远期的作者影响力的重视程度相对较弱，那么该指数从直观上应当具有以下性质。① 当作者较近期的影响力较高、中远期的影响力较低时，作者影响力的衡量值会较高，或者构造的h指数应当较高。② 当作者相对中远期的影响力较高、相对近期的影响力较低时，那么构造的h指数应当不会较高。③ 在对作者越近期的影响力越注重的h指数中，注重的程度应当可以变化，由于该h指数对作者越近期的影响力越注重，所以对作者近期的影响力的重视程度比对作者中远期的影响力的重视程度要高，同时注重程度越大，这种重视程度上的差异也越大，当注重程度逐渐减小时，对近期和中远期的重视程度的差异会逐渐减小。特别是随着注重程度的逐渐减小，如果把对各个时期的作者影响力的重视程度进行加总，那么对中远期作者影响力的重视程度在总的重视程度中所占的比例会逐渐增加，所以作者在中远期的影响力的作用与作者在近期的影响力相比，会逐渐增加，进一步地，如果使总的重视程度保持不变，那么该h指数对中远期作者影响力的重视程度会逐渐增加。④ 当注重程度等于0时，对各个时期作者影响力的重视程度相同，这是指对应于传统h指数的性质。

在具体构造对作者越近期的影响力越注重的h指数时，将使得不同的时段具有不同的权重，同时权重之和保持不变，并且权重是注重近期的。其中，注重近期不是指注重距离考察时间较近的某个时间点，而是距离考察时间越近越重视，因此，距离考察时间越近的时刻或时间段被赋予更高的权重。由于权重对作者越近期的时段越注重，对近期时段的重视程度比对中远期时段的重视程度要高，同时注重程度越大，这种重视程度上的差异也越大，当注重程度减小时，对近期和中远期的重视程度上的差异也减小，将权重对近期的注重程度记为a。进一步地，将作者论文的被引次数按照各个时段的权重加权求和并降序排列，按照传统h指数的方法可以构造相应的h指数，将该指数定义为注重作者近期影响力的h指数。从直观上考察，由此构造的注重作者近期影响力的h指数，具有上述对作者越近期的影响力越注重的h指数应当具有的四个性质。

（1）当作者比较近期的影响力较高、中远期的影响力较低时，假设作者较近期的论文数较多，同时每篇论文的被引次数也较高，那么作者在近期的影响力较高。由于文章的被引次数会处于不同的时间段，这样对于该作者而言，将其每篇文章的被引次数分别进行加权求和后，按照得到的和值降序排列，那么发表时间和考察时间相对较近的文章，其被引次数也处于距离考察时间较近的时段，所以具有较高的权重，那么这些文章对应的和值会较高。因此，在求h指数时，由于作者在比较近期发表的文章数量较多，同时这些文章的被引次数较高，那么得到的h指数也会较高。

（2）当作者相对远期的影响力较高、相对近期的影响力较低时，假设作者较远期的时候发表的文章数量较多，在假设被引半衰期为5年的情况下，每篇文章获得的被引次数会处于距离考察时间较远的时段，所以都具有较小的权重，那么这些文章对应的被引次数的加权和值会较小。因此，尽管作者较远期的文章数量以及每篇文章的被引次数均较多，得到的h指数也是偏低的。对于作者较中期时段的影响力较高、在其余时段的影响力较低的情形，仍然假设作者发表的文章数量较多，并且作者较中期时段得到的被引次数较多，或者说作者的论文较中期的时段得到的被引次数会较多，对于每篇论文而言，如果中期的被引次数较多，其余时段的被引次数较少，那么论文的被引次数的加权和值不会偏高。如果中期的被引次数与其余时段的被引次数均不多，那么被引次数的加权和值也不会偏高。此外，也存在中期被引次数较少，近期被引次数较高的情形，但是这种情形会相对较少，否则作者在近期的被引次数会相对较高，这样尽管该篇论文的被引次数的加权和值会相对较高，但是由于这类论文的数量相对较少，对于h指数的影响或者决定作用并不高，这样得到的h指数仍然是中等的。只有当作者发表的文章数量较多，并且作者在近期的被引次数较高时，得到的h指数才是较高的。上述在第一种性质中所讨论的情形符合这种要求。同样，对于作者发表的文章数量较多且作者在远期的被引次数较多时，得到的h指数是偏低的，在对第二种性质的考察中，当作者远期的影响力较高且近期的影响力较低时，所讨论的情形也符合这种要求。

（3）可以通过改变权重对近期时段的注重程度a来改变得到的h指数对近期的注重程度。如，当a减小时，尽管中远期时段的权重低于近期时段的权重，但是两者的差异会减小。如果对各个时段的权重进行求和，那么中远期时段的权重占权重之和的比例会增加，与近期时段的权重相比，中远期时段的权重的作用会增加。如果使权重之和保持不变，那么中远期时段的权重会增加，当作者中远期的影响力较高、近期的影响力较低时，假设作者发表的文章数量较多，并且作者中远期得到的被引次数较高，近期的被引次数较低，对于每篇论文而言，由于当中远期时段的权重增加时，近期时段的权重会减小。由此，每篇论文的被引次数的加权和值会增加，由于论文的数量是较多的，得到的h指数也会增加。作者中远期的影响力较高、近期的影响力较低，说明此时h指数对中远期影响力的重视程度增加，对近期影响力的重视程度减小，所以h指数对近期影响力与中远期影响力的重视程度的差异会减小，这样h指数对近期影响力的注重程度会减小。同理当a增加时，如果使权重之和保持不变，那么中远期时段的权重会减小，仍然考察作者中远期的影响力较高、近期影响力较低的情形，当中远期时段的权重减小时，每篇论文的被引次数的加权和值在总体上会减小，得到的h指数也会减小，说明此时h指数对中远期影响力的重视程度减小，对近期影响力的重视程度增加，所以h指数对近期影响力与中远期影响力的重视程度的差异会增加，这样h指数对近期影响力的注重程度会增加。由此，可以利用权重对近期的注重程度a，来对构造的h指数对近期的注重程度进行表征。

（4）当a=0时，各个时段的权重相等，由此得到的h指数对应于传统的h指数，对各个时段的作者影响力具有相同的重视程度。如，对于作者中远期的影响力较高、近期影响力较低的情形，仍然假设作者的文章数量较多，并且作者中远期得到的被引次数也较多；对于作者近期的影响力较高、中远期影响力较低的情形，相类似地，也假设作者近期得到的被引次数较多，那么两种情形下得到的h指数会是近似相等的，说明得到的h指数对中远期以及近期的作者影响力的重视程度是相同的。这样从直观上，构造得到的h指数能够具有注重作者近期影响力的h指数应当具有的性质，如果这些性质对于注重作者近期影响力的h指数的描述是全面的，那么可以认为得到的h指数是一种注重作者近期影响力的h指数，并且可以利用在确定各个时段的权重时对近期的注重程度a来调节得到的h指数对近期影响力的注重程度。

需要指出，在上述的直观认识中只是选取了某些特例来进行说明，需要对该指数的合理性与有效性进行进一步检验；在上述讨论中均假设作者的文章数较多，这和传统h指数的性质是一样的，否则如果作者的文章数量较少，尽管作者的影响力较高，但是利用h指数来对作者的影响力进行表征时，h指数是偏低的；另外，在上述讨论中，得到的h指数的取值是相对意义上的高或者低，是在得到的所有h指数的取值范围中的相对大小，这和传统h指数的取值大小相一致，也是在所有传统h指数取值中的相对大小。

对于作者在中期时段的影响力较高、在其余时段影响力较低的情形，从根本上是由于对中期时段赋予的权重是中等的，这样得到的h指数会是中等的。另外，当a减小时，中远期时段与近期时段的权重差异会减小，中远期时段权重占权重总和的比例会增加，当权重总和保持不变时，中远期时段的权重会增加，而近期时段的权重会减小，以至于当a=0时，近期时段的权重与中远期时段的权重会相等。在这个过程中，如果在权重的构造方式中，在保持权重总和不变的同时，使得中期时段的权重近似保持不变，那么当a=0时，由于近期时段的权重与中期时段的权重相同，此时近期时段的权重也会是中等的。其中，权重取值为中等时，仍然是相对意义上的中等，当a任意取值时，在各个时段权重的所有取值中的相对大小，这样对于作者在近期的影响力较高、在中远期影响力较低的情形，由于此时对各个时段的重视程度相同，并且近期时段的权重是中等的，那么得到的h指数也会是中等的，而这时的h指数对应于传统的h指数。但是，如果能够认为当a=0时，这里构造得到的h指数会转化成为传统的h指数，那么对于作者在近期影响力较高、在中远期影响力较低的情形，传统的h指数的取值应当是较高的，而此时得到的h指数却是中等的。由此，从直观上需要指出这是文中构造得到的h指数的缺陷，从根本上是由于对各个时段进行加权的方式造成的，如，使得各个时段的权重之和保持不变，但是从直观上，使得各个时段的权重之和保持不变应当具有必要性，目的是为了保证当a变化时得到的h指数仍然具有可比性。

2 权重的确定

在对各个时段的权重进行具体确定时，可以对各个时段的重要性分别进行比较，由此建立关于重视程度的判断矩阵。［2］在通过一致性检验的基础上，各个时段的权重为判断矩阵的最大特征值所对应的特征向量，为了满足对作者近期影响力注重的要求，越近的时段应当被赋予更高的权重。同时如果提高对近期的注重程度，那么近期时段的权重与中远期时段的权重的差异应当增加，反之权重的差异应当减小，这些均可以通过在判断矩阵中对相邻时段赋予不同的重要性以及调整重要性之间的差异来体现。假设将考察的时间范围划分为5个时段，其中划分的时段数可以任意选取，当对近期的注重程度较低时，使得判断矩阵右上部的元素均小于1，对于矩阵右上部的同一行中的任意两个相邻元素，使得左侧元素大于等于右侧元素；对于同一列中的相邻元素，使得上方元素小于等于下方元素，从而判断矩阵具有较好的一致性，这样得到的权重也能够更好地体现上述对作者近期影响力的注重要求，在此基础上使得矩阵元素在整体上取1/2到1/9之间较大的数值（见图1）。

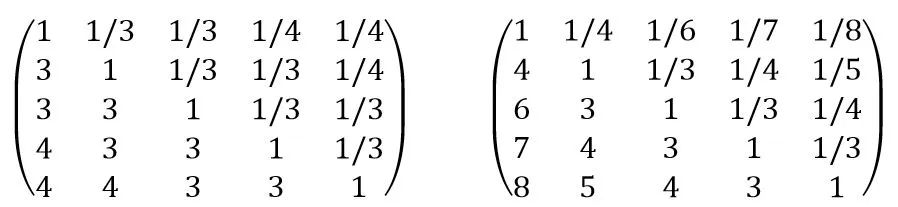
图1 判断矩阵的建立

在图1中，左边矩阵的最大特征值所对应的特征向量为（0.3058,0.5149,0.8168,1.2799,2.0826），最大特征值为5.3906，并且一致性比率为0.0872，能够通过一致性检验，取该特征向量的分量为各个时段的权重。需要指出，只按照上述对元素取值的要求来建立判断矩阵时，未必能够通过一致性检验，如果不能通过，还需要对元素的取值进行调整，而同时满足上述对元素取值的要求，以及使得判断矩阵能够通过一致性检验的取值调整空间从直观上是存在的。另外，正是因为满足这种重视程度之间的一致性，对元素取值的上述要求或者是对作者近期影响力注重的要求才能实现，否则得到的权重未必能够具有越近期越重视的性质。如，为了体现权重对近期时段的注重，必须要使判断矩阵右上部分的元素都小于1，但是按照上述的取值要求，矩阵中a21×a15有可能大于1，这样与a25＜1就不一致。那么，由该判断矩阵得到的权重既体现了这种不一致也体现了a25＜1这两种性质，甚至如果这种不一致程度较高，那么就未必能够有效地体现a25＜1，所以满足一致性检验时得到的权重才是满足对作者近期影响力注重的要求的权重。相类似地，当对近期的注重程度较高时，使矩阵元素在整体上取1/2到1/9之间较小的数值，如图1中右边的判断矩阵，此时矩阵最大的特征值所对应的特征向量为（0.1727,0.4262,0.7764,1.3103,2.3144），最大的特征值为5.3290，并且一致性比率为0.0734，能够通过一致性检验，在建立判断矩阵时也需要在满足上述取值要求的同时对判断矩阵的元素进行调整，以使判断矩阵能够通过一致性检验，否则由该判断矩阵得到的权重未必能够满足对近期时段作者影响力注重程度增加的要求。而在实际取值时，满足上述取值要求并使判断矩阵能够通过假设检验的调整空间也是存在的。可以对图1中右边矩阵的第一行进行取值，使得最远时段与其余各个时段的相对重要性能够满足注重近期时段且注重程度较高的要求，对其余行进行取值时，使取值与第一行取值所表示的相对重要性不相冲突，从而使判断矩阵能够满足一致性要求。经过初步检验，这种取值是存在且不唯一的，由此得到的权重才是满足注重要求的权重。

能够注意到，由图1右边矩阵得到的权重对近期时段会更为注重，如，对于任意两个时段而言，较近时段与较远时段之间的权重差异均会更高。需要指出，为了保证得到的h指数之间具有可比性，需要使考察的时间范围相同，同时还需要将考察的时间范围划分为相同的时段，这样得到的权重也才会具有可比性。

另外，当注重程度等于零时，各个时段具有相同的权重，由于要使构造得到的h指数能够转化为传统的h指数，要求各个时段的权重相等且等于1。同时，为了保证得到的h指数具有可比性，需要使各个时段的权重之和保持不变，这样当分段数为5时，各个时段的权重之和均应等于5，这也是图1中两个判断矩阵的特征向量没有取为分量之和等于1的原因。

由此，可以利用判断矩阵来对权重进行确定，其优点是在赋予各个时段的权重时可以较为灵活，但是由于当对象较多时会对相互之间的相对重要性判断带来影响，采取这种方法时对时段数量的要求较高。同时，由于在赋予各时段权重后，如需要调整注重程度，需重新建立判断矩阵，由此来重新赋予各个时段的权重，除了计算量可能较大之外，也不一定能够保证注重程度能够连续变化。因此，在确定权重时还可以尝试建立某类关于注重程度的函数，使注重程度作为某种响应变量，当该函数的参量以及函数自身连续变化时，注重程度也能够连续变化，这样不仅在确定权重时计算量会减小，而且能够使注重程度连续变化。特别地，在建立函数时可以使注重程度在-1到1这个区间内连续变化，取值越大，注重程度越高，而当注重程度的取值为负数时，表示对远期的作者影响力更为重视，当取值为零时，表示对各个时段的注重程度相同。除此之外，在利用判断矩阵来确定权重时，能够按照注重要求来大致调节对近期的注重程度，如在图1中左侧矩阵对近期的注重程度会弱于右侧矩阵，但是如果需要准确知道此时注重程度的大小与差异，还需要给出相应的衡量方式。由此，确定权重时使注重程度能够连续变化会具有一定的优势，能够建立相应的权函数（见图2）。

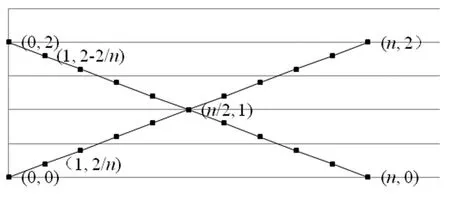
图2 注重程度连续变化时的权重确定

在图2中，横轴为划分的各个时间段的序号，分别为第0时段至第n时段，纵轴为各个时段的权重，权函数为y=2ax/n+1-a，其中a的取值范围为-1到1，图中斜率为负数的直线段对应于a=-1时的情形。这时近期时段的权重小于远期时段的权重，并且远期时段与近期时段的权重差异也是最大的，说明此时对远期的重视程度是要高于对近期的重视程度，并且对远期的注重程度也是最高的，其中的注重远期意味着对距离考察时间或者第n时段越远的时段会越重视。随着斜率绝对值的减小，由于远期时段的权重仍然高于近期时段的权重，并且远期时段与近期时段的权重差异会减小，因此对远期的注重程度会逐渐减小。当斜率等于零时，a=0，此时各个时段具有相同的权重且等于1；当斜率为正数时，a＞0，这时近期时段的权重大于远期时段的权重，说明此时的权重是注重近期的，并且随着斜率的增加，近期与远期时段的权重差异也会增加，由此，权重对近期的注重程度也会增加。图中斜率为正数的直线段为a=1时的情形，这时对近期的注重程度达到最大。在图2中，当直线段的斜率或者a连续变化时，权重对近期的注重程度也会连续变化，可以利用a来表征对作者近期影响力的注重程度：当a＞0时，权重是注重近期的，并且a越大，对近期的注重程度越高；当a＜0时，权重对远期注重，并且a的绝对值越大，注重程度越高；而当a=0时，权重对近期或远期的注重程度均等于零。

另外，需要使各个时段的权重之和保持不变，这样当a固定时，每篇论文的被引次数的加权和值是建立在相同的权重基础上。由此，对于同一作者以及不同作者而言，得到的h指数会具有可比性。同时，当a变化时，由于权重之和维持不变，只是各个时段的相对重视程度会发生改变，这样每篇论文的被引次数的加权和值以及得到的h指数在数量上仍然会有可比性。在图2中，各个时段的权重之和为2a（1+2+...+n） /n+（n+1）-a（n+1）=n+1，因此，权重之和与 a无关。同样地，为了使a=0时得到的h指数能够转化为传统的h指数，当a=0时需要使各个时段的权重相等且等于1，因此，文中将权重之和取为n+1。

3 合理性检验

在确定各个时段的权重之后，利用传统h指数的定义可以构造出对作者近期影响力注重的h指数，并进行合理性检验以及实证分析。如，当注重程度较高时，某一领域近期的代表作者的h指数的排序会相对靠前；当注重程度较低时，该领域的奠基性作者的h指数的排序会相对靠前，这样只利用h指数就可以对两类作者进行识别。

在知网中可以得到每位作者的每篇论文的被引次数以及这些被引次数的施引年份，由此可以得到每位作者总的被引次数以及这些被引次数的年代分布，利用每篇论文的发表时间，也可以得到每位作者发表的总的论文数以及这些论文的年代分布。同时，由于为了明确不同时期的代表作者，文中只是选取了被引次数相对较高的作者作为考察对象，其中数据的获取时间为2018年1月，考察的领域为中国知网中的图书馆学及图书馆事业这个分类。

在作者被引次数的年代分布中，由于选取的对象为被引次数相对较高的作者，这些作者的影响力也会相对较高，当被引次数的年代分布在足够长的考察时间范围内可以近似为单峰的情形下，能够假设被引次数最高的年份是作者具有较高影响力的年份，由此能够近似得到每位作者影响力较高的年份（见图3）。当被引次数较高时，作者在该年度的影响力也会较高，而文中只是选取了最大年度被引次数来大致确定作者影响力较高的时间范围。对于在近期时段影响力较高的作者，由于作者在近期时段得到被引次数较多，被引次数的年代分布未必能够近似为单峰，但是在该情形下最大年度被引次数通常会出现在近期时段，所以在这里仍然利用最大年度被引次数来对作者影响力较高的时间范围进行大致确定。另外，在此过程中，如果作者在多个年度的被引次数均为最大年度被引次数，可以任意选取其中某个年份来近似确定作者具有高影响力的时间范围。

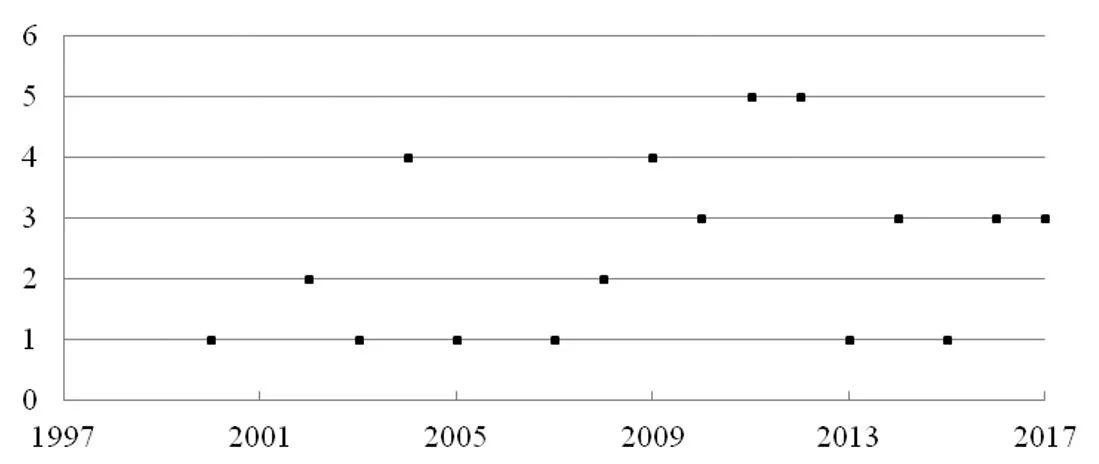
图3 每位作者被引次数最高的年份

在图3中，纵轴为在某个年度被引次数取为最大年度被引次数的作者的数量，在此基础上可以对考察的时间范围进行分区，分区的数量以及每个区间的长度可以任意选取。文中将横轴划分为图中的5个时段，其中最远的时段为2001年及其之前的时间范围，这样的划分能够使得在求每篇论文的被引次数的加权求和时，所需的权重均能够构造得到。在这里得到的h指数是截至2017年的作者的h指数，这和截止到某年度的传统的h指数也是相同的。同时，在这种分区的基础上也可以探讨当对作者近期影响力的注重程度发生变化时的每位作者的排序情况，由此来检验得到的h指数的合理性，另外考察的时间范围以及相应的分区需要保持不变，这样当对近期的注重程度发生变化时，确定的权重以及得到的h指数在数量上会具有可比性。

取权重对近期的注重程度a=0.8，由于可以利用权重对作者近期影响力的注重程度来对得到的h指数对其进行表征，此时得到的h指数对近期的注重程度应当是相对较高的。如果利用注重程度连续变化时的情形来对权重进行确定，那么各个时段的权重分别为0.2,0.6,1,1.4,1.8，其中n等于4，那么在此基础上根据作者每篇论文的被引次数及其年代分布可以得到h指数（见图4）。

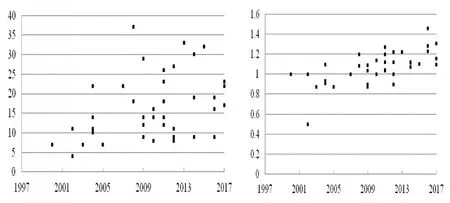
图4 构造得到的每位作者的h指数

在图4左边的情形中能够注意到，当对近期的注重程度较高时，越是在近期具有高影响力的作者的h指数会具有越高的趋势，所以能够在一定程度上体现出构造得到的h指数具有对作者越近期的影响力会越重视的倾向。但是也能够注意到，如，第4时段的作者与第3时段的作者相比，h指数在整体上会相对偏低，而这和上述直观认识中的讨论是不相符合的。从直观上，由于得到的h指数对作者越近期的影响力越重视，尽管某位作者较近期的影响力较高，其余时段的影响力较低，同时另外一位作者近期的影响力较高，那么后者的h指数应当高于前者才能与得到的h指数的注重近期的性质相符合。因此，第4时段的作者的排序应当高于第3时段的作者，并且其排序在所有时段中应当是最为靠前的。但是需要指出，在直观认识中所讨论的每位作者在不同时期具有的较高影响力，是这些影响力均较高、并且对这些影响力之间的相对高低不进行区分的意义上的较高影响力，这样才会有相应的认识结果，而实际上尽管每位作者的影响力均较高，但是在程度上仍然可以有较大的差异。尽管得到的h指数注重作者近期的影响力，但是如果某位作者较近期的影响力较高，并且显著高于近期影响力也较高的另一位作者的影响力，那么会存在前者的h指数高于后者的情形，而这与得到的h指数对作者越近期的影响力越重视的直观认识是不相矛盾的。但是对于影响力均较高的这些作者而言，如果对这些作者进行选取时具有一般性，得到的h指数至少应当具有在近期影响力较高的作者的h指数会高于在远期影响力较高的作者的h指数的趋势，其中的近远期是相对意义上的，所以在整体上随着时段的由远而近，得到的h指数应当有逐渐增加的趋势。

由于只考虑注重近期不一定能使在不同时期分别具有较高影响力的作者完全按照其高影响力所在的时段进行排序，文中需要利用某种方式来衡量得到的h指数是否满足对于越在近期具有较高影响力的作者，其得到的h指数的排序会越靠前的要求，以及对满足的程度进行衡量，由此来衡量构造方法的合理性与有效性。由于每位作者均有所属的具有较高影响力时段的序号以及得到的h指数与该作者相对应，在这里利用两者之间的等级相关系数作为标准来衡量构造的方法对在不同时期分别具有较高影响力的作者的识别程度。如，对近期的注重程度较高时，越在近期时段具有较高影响力的作者会越靠前，这样在某一领域中最近期的代表性作者的h指数的排序会最为靠前，从而能够尝试对该类作者进行区分。在求两变量的等级相关系数时，没有将作者所属的高影响力时段相同的情形计入在内，目的是只考察作者具有高影响力的时段与得到的h指数之间的等级关系，所以文中等级相关系数为r=s/t。其中，s为作者具有高影响力时段的序号与作者的得到的h指数形成的同序对的个数，对于时段序号差值为零的情形以及作者得到的h指数的差值为零的情形均不计入在内。如果将任意两个数对作为一组，并将这些组的个数称为总组数，那么t等于总组数减去时段序号差值为零的情形的个数，这样t实际上也等于形成的同序对与异序对以及得到的h指数差值为零的情形的总数，这样时段序号的差值以及得到的h指数的差值同时为零的情形也是不计入在内的。由此，该等级相关系数是只对在不同时段具有高影响力的作者的高影响力时段与其得到的h指数之间的相关性进行衡量，当两位作者属于同一高影响力时段时不对其进行比较，该系数的取值范围为0到1，该系数越高说明同序对的个数越多，这样作者所属时段与得到的h指数的正相关性会越高，当系数等于1时，说明近期时段具有高影响力的作者的h指数均会高于远期时段的作者的h指数。其中，远近均为相对意义上的远近，对于图4左边的情形，该等级相关系数为0.629。

影响该等级相关系数的因素包括上述每位作者的影响力均较高，但是在程度上仍然存在较大差异时，可以对该因素进行剔除，从而减少由作者在较远时段的影响力较高，且显著高于在较近时段具有较高影响力的作者其h指数排序靠前的情形出现。由此，能够提高作者高影响力所属时段与得到的h指数之间的一致性，或者能够使相关系数有所提高。在图4右边的情形中，当权重对近期的注重程度a=0.8时，可以得到每位作者此时的h指数，当权重对近期的注重程度等于零时，各个时段的权重相等且等于1，可以得到作者此时的h指数，且为传统的h指数。将前者除以后者作为纵轴并记为h’，在这里利用前者除以后者来减少上述由作者自身影响力的高低所带来的对作者排序的影响，从而会更注重得到的h指数的构造方式对于作者排序的影响。在图4中能够注意到，与左图相比，对于越在近期具有较高影响力的作者，其排序会越靠前的要求，右图满足的程度会更高，并且可以得到此时的等级相关系数为0.759，其中需要将数对中得到的h指数更换为h’。在图5中权重对近期的注重程度a=-0.8，得到的h指数对远期的注重程度相对较高。仍然利用注重程度连续变化时的情形来对权重进行确定，得到的结果与a=0.8时的情形相类似，可以得到左图与右图的等级相关系数分别为0.535与0.788，其中需要将s中的同序对的个数更换为异序对的个数。

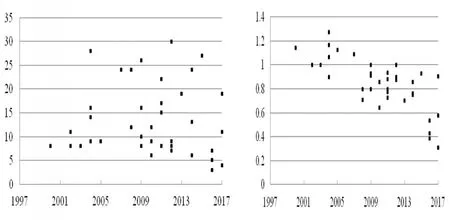
图5 构造得到的每位作者的h指数

除了由作者影响力的差异所带来的影响外，对作者具有高影响力时段的确定方式也会影响作者的排序情况。文中采用最大年度被引次数来对作者影响力较高的时间范围进行确定的方式是粗糙的，如，会存在这样的情形，从最大年度被引次数所在时段开始向近期或者向远期的较长时间范围内，作者都会具有较高的影响力，这样在确定作者具有高影响力的时段时仅由最大年度被引次数来进行确定存在偏差。由此会出现这样的结果，如，本应属于在较近时间范围内具有较高影响力的作者会被当作在中期时段具有较高影响力的作者进行处理，而此时作者得到的h指数以及标准化后的h指数均可能是较高的，其中标准化后的h指数是上述得到的h指数与传统h指数的比值，从而会造成作者所属的具有较高影响力的时段与得到的h指数以及标准化后的h指数之间的排序不一致的情形出现，或者说等级相关系数的取值还会受到高影响力时段的确定方式的影响，这也是在图4与图5的右图中等级相关系数仍然没有等于1的原因之一。

另外，对各个时段的加权方式也会对等级相关系数产生影响，文中利用在时段上的线性加权，会造成尽管权重对作者近期影响力的注重程度很高，但是比较近期与近期两个时段的权重差异并不会偏低的情形出现。由此，对于在比较近期影响力较高的作者，且其影响力显著高于近期影响力较高的作者的情况，尽管可以利用标准化后的h指数在一定程度上消除作者影响力自身的影响，但是由于这种线性加权以及h指数自身取值的相对稳定性，在比较近期影响力较高的作者得到的h指数与其传统h指数之间的差异可能会具有高于在近期影响力较高的作者的两种h指数之间的差异的倾向。如，在图4右图中的两位作者，具有高影响力的时段分别为2014年与2010年，得到的h指数与传统的h指数分别为9与8以及16与14，假设作者的某篇论文的被引次数为c，由于作者是在较近期与近期的影响力较高，在求被引次数的加权和值时是将每单位被引次数均乘以相同的某个大于1的系数d，这样这篇文章的加权和值为cd，并且与这篇文章的被引次数的差值为c（d-1）。由于与后者的影响力相比，前者的影响力会显著偏低，可以认为后者每篇论文的被引次数在总体上会高于前者，所以每篇论文的加权和值与其被引次数的差值在总体上也会高于前者，这样对于后者而言，其得到的h指数与传统h指数的差异也会大于前者两种h指数之间的差异。因此，可能仍然会使得在较近期影响力较高的作者其标准化后的h指数高于在近期影响力较高的作者，从而对等级相关系数会具有抑制作用。

文中对h指数进行构造的最终目的是使当对近期的注重程度较高时，近期代表性作者的h指数的排序会靠前，当对远期的注重程度较高时，奠基性作者的排序会靠前。同时注重程度可以连续变化，由此来对每位作者在不同注重程度时的影响力分别进行衡量，其中的注重程度是指h指数对作者近期影响力的注重程度，同时这种衡量方法应当适用于影响力的不同情况，而不只限于作者影响力均较高的情形。另外，当作者的影响力均较高时，需要在这些影响力可能存在较大差异的情况下，仍然可以将不同时段的代表性作者识别出来，可以考虑利用上述等级相关系数来衡量构造方式的有效性，以及需要在以上影响因素的基础上进行构造方式的改进，使得等级相关系数能够有所提高。