扩散的多用户分子通信系统的信道容量分析
程 珍,章益铭,赵慧婷,林 飞
(浙江工业大学 计算机科学与技术学院,杭州 310023)
1 引 言
近年来,纳米技术发展迅猛,这为作为纳米级通信基本单元的纳米机器(Nanomachine)[1]的制造铺平了道路.由于单个纳米机器的功能和通信能力相当有限,能够将这些纳米机器互联协作以便完成更复杂任务的纳米级通信网络[2,3]被提出.在微纳米尺度上,由于电磁信号波长和天线尺寸比例等因素的限制,基于电磁的纳米通信并不适用[4],而以分子作为信息传递载体的分子通信模型被普遍认为最具前景的解决方案之一[5].
在分子通信中,分子可以遵循特定的路径或由流体介质引导到达目的地[6],其传播方式通常被限制于扩散,例如昆虫之间通过弥漫在空气中的信息素交流[7]或活细胞之间的钙信号传导[8].作为纳米通信技术的新前沿—扩散的分子通信(Diffusive Molecular Communication,DMC)一直受到重视和关注.在DMC中[9],发送方纳米机器(Transmitter Nanomachine,TN)将被调制和编码的信息分子释放到流体介质中,分子的运动遵循布朗运动规则,通过自由扩散进入接收方纳米机器(Receiver Nanomachine,RN)的接收范围并可能被RN接收.
近年来,较多的学者对DMC模型进行了详细的研究.在信道模型方面,Pierobon等人[10]则是为分子通信引入了一种新的包含发射机、信号传播、接收机三个模块的物理端到端DMC模型,并给出了该模型的归一化增益及时延的性能分析.对于信道噪声,Akyildiz等人[11]为DMC的计数噪声及分子采样噪声建立了物理模型和随机模型,并评估了随机模型捕获产生噪声的物理过程的行为能力.在信道容量方面,Kadloor等人在文献[12]中提出了一个加性逆高斯噪声信道模型,并分析了该模型信道容量的上限和下限.Kabir等人[13]针对基于分子浓度编码的DMC模型,分析了前一个时隙对当前时隙干扰的信道容量.而Pierobon等人[14]为DMC模型的信道容量提供了以系统带宽及TN每个时隙发送的分子个数为参数的数学表达式.Meng[15]等人提出了二元DMC模型,考虑了多个时隙对当前时隙的码间干扰(Inter-symbol Interference,ISI),导出了使互信息最大化的最佳判决阈值.Yeh[16]等人针对端到端的多时隙ISI的DMC模型,提出了最优检测方案.Cheng[17]等人考虑了多时隙的ISI以及不同时隙TN发送1或0的概率不同情况下,对二元DMC模型的信道容量进行了优化.
在多用户DMC模型中,多个TN共享相同信道,由于不同TN释放相同的分子,而相同信息分子具有不可区分性,用户间干扰(Inter-User Interference,IUI)不可避免地存在.Ergin[18]等人考虑了接收器吸收分子会饱和的情况,为多用户DMC系统引入了能计算RN接收分子预期数量的分析框架.Jiang等人[19]考虑了ISI和IUI的多用户分子通信模型,并对该系统比特错误率性能进行了分析,但文献[19]中仅仅讨论了两个用户以及一个码间干扰时隙的情况,应用场景相对简单;Meng[20]等人主要考虑了多输入多输出(Multiple-input Multiple-output,MIMO)系统中IUI的干扰类型,并假设ISI可以忽略,首次分析了MIMO分子通信系统的误码率.Koo等人[21]针对2×2MIMO分子通信系统,建立了基于ISI和链路间干扰(Inter-link Interference,ILI)两种干扰类型的信道模型,提出了MIMO系统的检测算法,分析了信噪比和比特错误率的性能,但该论文并未对系统的信道容量进行理论和仿真分析.
因此,在上述研究基础上,我们研究了DMC模型在ISI和IUI两种类型干扰及多时隙情况下的信道容量以及比特错误率.首先,推导了ISI和IUI两种类型干扰总和的数学表达式;其次,采用最小误差准则求得最佳判决阈值,从而得到系统的互信息表达式;最后,根据仿真结果,可以通过控制不同参数的值使得该系统的信道容量达到最大化,同时比特错误率最低.这一思路,对扩散的多用户分子通信系统的研究有重要的科学意义.
2 系统模型
图1为多用户DMC系统拓扑图.如图1所示,该系统由M个TN构成的信息源和一个RN组成.第i个TN,用TNi表示,它到RN中心的距离记为di,R为RN半径.我们假定这些TN具有相同的物理特性,但这里并不讨论其具体的物理结构.假设TN与RN在时间上完全同步,同时不考虑分子间的碰撞效应,这些分子一旦被RN接收后会被立即吸收,不再存在生物环境中.此外,假设所有分子被接收的事件发生在离散时间点.分子传输时间被划分为大小相同的时隙,记为t=nts.其中,t为信息传输的时间,ts为每个时隙持续时间,n为所划分的时隙的个数.
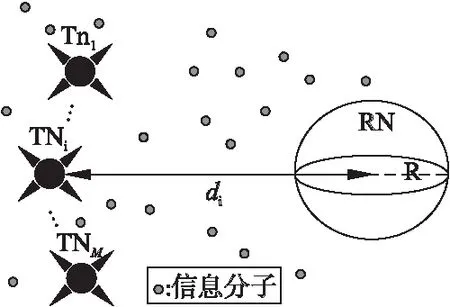
图1 多用户DMC系统拓扑图
在本文中,我们采用OOK(On-Off Keying)作为调制技术.即在每个时隙开始时,TNi释放数量为Qi的分子代表发送比特1,不释放任何分子表示发送比特0.信息分子被释放后,经由流体媒介自由扩散至RN的检测范围.分子的运动遵循布朗运动规则.我们考虑一维环境中的分子扩散情况,在分子从释放到进入RN的接收范围的扩散过程中,描述任一个分子在t时刻之前从TNi到达RN的概率记作Fi(t),表示如下[22]:
(1)
其中,di表示两个纳米机器TNi和RN间的距离,D为生物环境的扩散系数,R为RN半径.由上述可知,当TNi在第(n-k)个时隙释放分子之后,该分子在第n个时隙被RN接收的概率Pi(k)为:
Pi(k)=Fi((k+1)ts)-Fi(kts)
(2)
其中,ts为每个时隙的持续时间,k∈{1,2,…,n-1}.特别地,TNi在当前时隙释放的分子在当前时隙被RN接收的概率为Pi(0)=Fi(ts).
在多用户DMC系统中,分子在被释放入流体媒介后,在忽略碰撞效应以及不考虑它们之间相互反应的情况下,所有分子的运动是相互独立的.假定TNi在第(n-k)个时隙释放的分子在当前第n个时隙被RN接收的数量用Ni(k)表示,根据上述公式(2)可知,Ni(k)满足如下二项分布,记作:
Ni(k)~B(Qi,Pi(k))
(3)
图2为Pi(k)与当前时隙相差的时隙个数k的关系图.设置D=100μm2/s,R=10μm,d=25μm,ts=1s,由图2可知,当Pi(k)较小,Qi充分大时,二项分布B(Qi,Pi(k))可以用对应的正态分布N(QiPi(k),QiPi(k)(1-Pi(k)))来近似逼近,则(3)式可表示为:
Ni(k)~N(QiPi(k),QiPi(k)(1-Pi(k)))
(4)
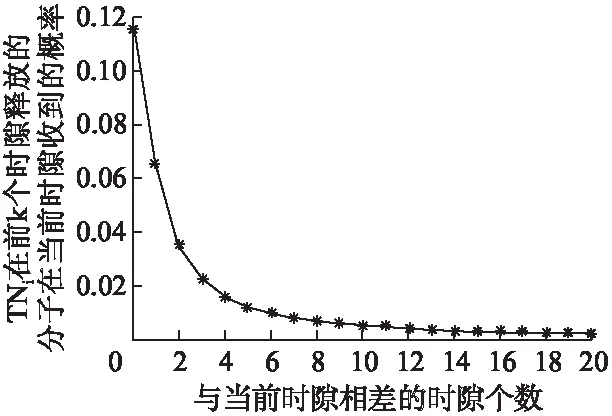
图2 TNi在前k个时隙释放的分子在当前时隙收到的概率Pi(k)与前面时隙个数的关系图
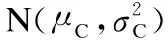
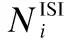
(5)
3 多用户DMC系统的信道容量分析
3.1 ISI分析
假设TNi的信息比特集用Si表示:Si={Si[1],Si[2],…,Si[n]},比特集彼此之间相互独立.由于我们采用OOK调制技术对信息进行编码,即在每个时隙开始时,当Si[n]=0时,TNi不释放任何分子代表发送比特0;当Si[n]=1时,TNi在第n个时隙释放的分子数量为Qi*Si[n]代表发送比特1.
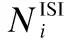
(6)
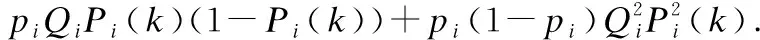
证明:由于Si[n-k]Ni(k)在发送比特1的情况下服从N(QiPi(k),QiPi(k)(1-Pi(k)),而在发送比特0时的值等于0.因此,Si[n-k]Ni(k)的均值μ为piQiPi(k).其方差σ2的计算公式为:
σ2=E[(Si[n-k]Ni(k))2]-E[Si[n-k]Ni(k)]2
(7)
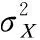
(8)
证毕.
(9)
3.2 IUI分析
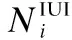
(10)
(11)
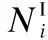
(12)
(13)
3.3 信道容量分析
本章节我们将采用信息论的方法讨论上述系统的信道容量,即信道能每秒无错误传送的最大信息量.我们首先建立基于DMC的二元假设检验模型,然后计算TNi和RN之间的互信息,而互信息的最大值即为系统的信道容量.
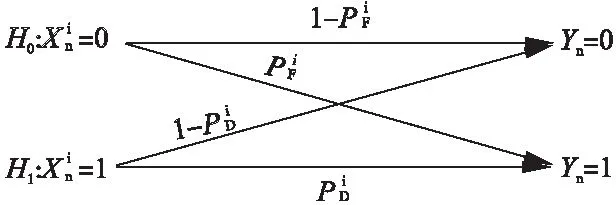
图3 基于DMC的二元假设检验模型
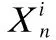
(14)
根据信息论的知识,结合公式(14)可得信道容量C的计算公式[15]如下:
(15)
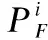
(16)
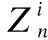
(17)
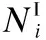
(18)
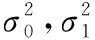
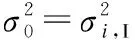
(19)
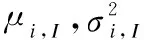
(20)
其中,P(H1)=pi,表示TNi发送比特1的概率,P(H0)= 1-pi代表TNi发送比特0的概率.P(z|H1)和P(z|H0)则分别对应这两个事件下RN收到z个分子的概率.用∧(z)表示似然比,由公式(20)可知,似然比计算公式为:
(21)
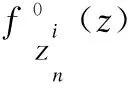
(22)
因此,根据公式(21)(22)我们可以得到似然比为:
(23)
结合公式(21)、公式(23),对等式两边取自然对数,可得:
(24)
利用公式(24),进一步求解z可得:
(25)
其中,η为的最佳判决阈值,即如果RN在当前时隙收到的分子总数yi[n]≥η,则RN输出1;如果yi[n]<η,则RN输出0.而参数A、B、C为:
(26)
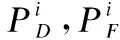
(27)
其中,Q(x)函数是标准正态分布的互补累计分布函数,定义如下:
(28)
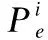
(29)
4 数值结果
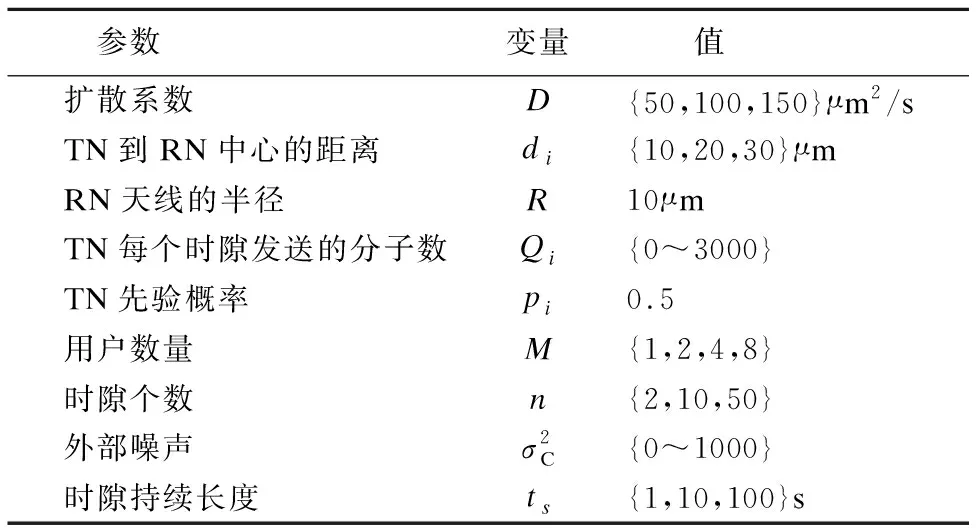
表1 参数取值范围
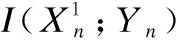
图5 Qj(2≤j≤4)取不同时互信息与Q1的关系
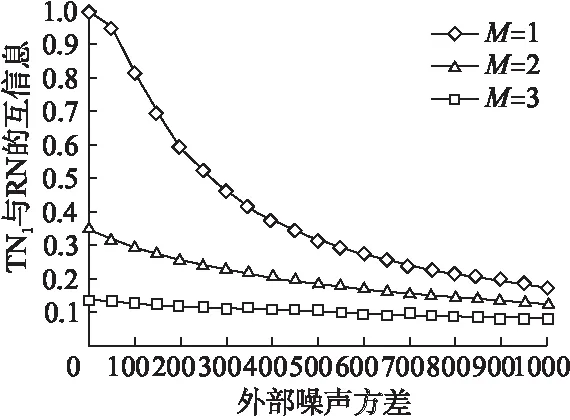
图6 M取不同时互信息与外部噪声方差的关系
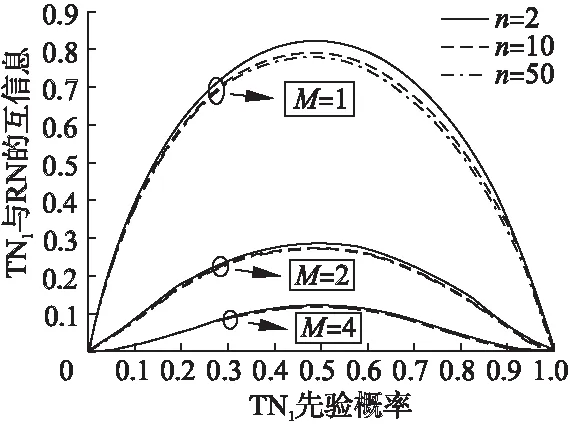
图7 n取值不同时互信息与先验概率p1的关系
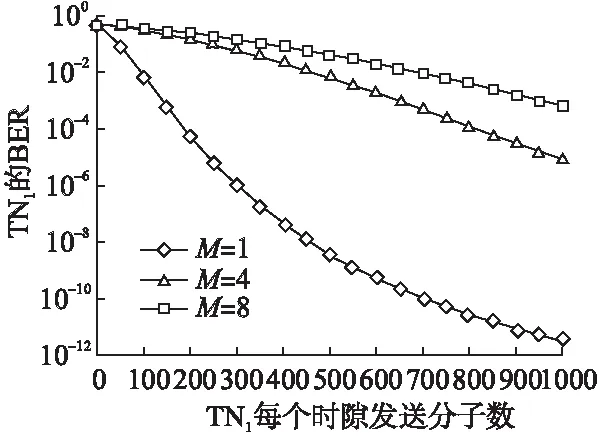
图8 M取不同时比特误码率与Q1的关系
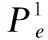
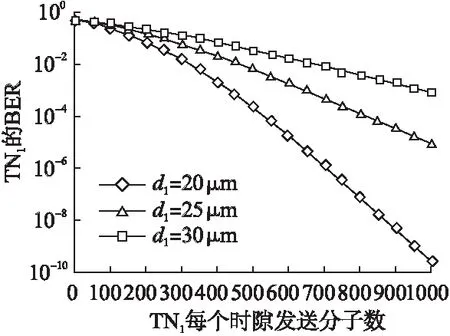
图9 d1取不同时比特误码率与Q1的关系
5 结 论
在本文中,我们首先通过对码间干扰ISI以及用户间干扰IUI的分析,得出多用户分子通信系统干扰总和的表达式;然后,采用最小误差准则得出接收方纳米接收器的最佳判决阈值以及系统的互信息;最后,通过实验仿真分析了不同的参数对多用户分子系统中TN1与RN的信道容量和比特错误率的影响.仿真结果表明,不同的参数包括TN1与RN之间的距离,TN每个时隙发送的分子数,用户数量,时隙个数以及外部噪声对系统性能的影响程度不同.其中,用户数M是多用户DMC系统通信效率的主要制约因素,外部噪声也限制着系统的信道容量,而时隙个数n的影响则相对较小.同时,我们也发现减小TN与RN的距离或增大TN每个时隙释放的分子数均能提高系统信道容量和降低RN接收该TN的BER.

