节点影响力下无标度网络谣言传播研究
刘亚州,王 静,2,潘晓中,付 伟
1(武警工程大学 密码工程学院,西安 710086 2(西安高科技研究所 计算机科学与技术系,西安 710086)
1 引 言
社交网络[1-3]的出现,使信息传播的渠道得到了极大的丰富,信息传播的内容也是良莠不齐,其中不乏对人们生活造成重大影响的信息,如谣言[4-6].随着社交网络的影响不断扩大,谣言在社交网络中的传播规律、传播行为[7]也逐渐引起学者的广泛关注,并对谣言在社交网络上的传播进行了一系列的研究.
国内外学者就谣言传播机理的研究开展了大量的研究工作,并取得了一系列的成果.王辉等[8]提出一种基于移动社交网络下的谣言传播模型,并且验证所提模型在匀质网络上传播时范围更广,速率更快;张彦超等[9]模拟信息在在线社交网络上的传播过程,分析不同类型节点在传播中的行为规律;朱张祥等[10]基于聚类系数可变的无标度网络环境对谣言传播进行了研究,发现谣言的传播能力与影响范围会随着社会加强正向效应、用户首次接触并相信谣言的概率、孤立节点密度以及初始传播节点的度的增大而增大.顾亦然等[11]提出一种SEIR谣言传播模型和一种重要熟人免疫策略.上述研究基本上都是假设节点状态的转变只受单一节点的影响,然而这往往与社交网络中谣言传播的真实情况不一致.实际谣言传播过程中节点对谣言态度的选择往往受所有邻居节点的共同影响,这是因为社交网络中节点接收信息的方式不再局限于口口相传,任何一个节点的所有邻居节点对谣言的态度可能不止一种,节点对谣言态度的转变是一个在各类节点共同影响作用下的综合过程.此外,由于不同节点对谣言认识程度不同以及社会加强作用的存在,导致不同节点影响力的非一致性,这种非一致性使节点对其它节点的影响力表现出不同的权重,节点选择相信并传播谣言对其它节点的影响表现
出一定的负权重,节点选择不相信谣言并辟谣对其它节点的影响表现出一定的正权重.目前,关于以上两个现实因素在社交网络中谣言传播的研究还非常少.
本文基于经典的SIR传染病模型[12],考虑节点影响力对谣言传播特性的作用,构建了谣言传播模型的S2IR模型,利用平均场理论[13,14],研究该模型在无标度上的传播动力学行为.随后利用改进的聚类系数较大的无标度网络对谣言在本文所提模型中的传播特性进行了仿真实验,并与传统的SIR模型进行了比较.
2 社交网络谣言传播模型S2IR
由于现实生活中大部分谣言具有一定的危害性[15],因此本模型中考虑社会加强作用为负向加强,即当谣言出现后,政府机构以及主流媒体对谣言持否定态度,现实中往往谣言涉及问题的重要性越大、谣言的模糊性越小,社会负向加强作用越强,用α(0≤α≤1)表示社会对某一谣言的负向加强,其表示为:
α=I×(1-A)
(1)
其中I(0≤I≤1)表示谣言所涉及问题对于网络中节点的重要程度,A(0≤A≤1)表示谣言所涉及问题的模糊性.
谣言在社交网络中出现时,节点对谣言态度的选择除了受邻居节点对谣言态度以及自身辨识能力影响外,社会负向加强因素也成为影响节点选择谣言的一个重要因素,由于法律或政策的原因,传播谣言可能使节点利益受损,节点存在相信谣言但不传播的可能性,此类节点对健康节点的影响程度与相信并传播谣言的节点对健康节点的影响程度明显不同.鉴于此,本文根据社交网络谣言传播特性,将社交网络中节点分为四类:健康节点S,表示节点对谣言情况未知,知晓节点I1,表示节点相信但并不传播谣言,传播节点I2,表示节点相信并传播谣言,免疫节点R,表示节点不相信并抑制谣言.
现实生活中的个体由于知识背景、教育水平以及兴趣等方面的不同,不同个体接触到谣言信息后对谣言信息的信任程度相应的也会不同.知晓节点I1虽然接触并相信谣言,但由于对谣言信息信任程度较低,选择不传播谣言,因此在谣言传播过程中对其它节点的影响程度较低,传播节点I2选择相信并传播谣言,对谣言信息的信任程度较大,在谣言传播过程中会对与其接触的节点进行说服,使被说服的节点相信谣言信息,对谣言在社交网络中的传播起促进作用,免疫节点R选择不相信并抑制谣言传播,会将不相信谣言的影响传递给与其接触的节点,对谣言在社交网络中的传播起阻碍作用.因此,由于不同节点对谣言信息信任程度不同,致使在谣言传播过程中对其它节点影响的权重不同,结合谣言的社会负加强作用,传播节点I2对其它节点影响力的权重取-1,免疫节点R对其它节点影响力的权重取1,由于知晓节点I1虽然相信但并不传播谣言,因此对其它节点的影响权力重为0,同样健康节点S对其它节点的影响力权重也为0,用Nk(S)、Nk(I1)、Nk(I2)、Nk(R)分别表示度为k的节点的邻居节点中健康节点、知晓节点、传播节点、免疫节点的数目,则邻居节点对度为k的节点总的影响值M(k)可表示为:
M(k)=Nk(R)-Nk(I2)
(2)
对于健康节点S而言,当M(k)>0时,表示邻居节点对健康节点的影响体现为不相信谣言,则S类节点转化为免疫节点R的概率P1可表示为:
(3)
其中P(k)(0≤P(k)≤1)为度为k的节点对谣言的辨识能力,α为社会对谣言的负向加强,实际中当一个谣言出现时,对谣言具有很高的辨识能力和对谣言具有很小的辨识能力的个体数量占总个体数量的比例均较小,大部分节点对谣言的辨识能力相差不大,再者度较大的节点往往是较早加入到网络中、具有较好教育背景的个体,此类节点对谣言往往也具有较高的辨识能力,因此节点对谣言的辨识能力大小与节点的度呈正相关,节点对谣言的辨识能力大致服从正态分布.α为社会对谣言的负向加强,当α变大时,社会对谣言的负向加强增强,健康节点转变为免疫节点的概率相应增大.通过式(3)可以看出,当健康节点的邻居节点中免疫节点数目增大时,即当Nk(R)增大时,健康节点转变状态成为免疫节点的概率P1也会相应增大,这主要由于邻居节点中免疫节点数目增大时,对健康节点的免疫影响力会产生累积效应,使健康节点更容易转化为免疫节点.
对于健康节点S而言,当M(k)<0时,表示邻居节点对健康节点的影响体现为相信并传播谣言,则S类节点转化为传播节点I2的概率P2可表示为:
(4)
由P2公式可知,随着社会负向加强作用α减小、节点对谣言的辨识能力P(k)减小以及邻居节点中传播节点I2增大,健康节点转变为传播节点的概率均会增大.
对于健康节点S而言,当M(k)=0时,表示邻居节中相信并传播谣言的节点与不相信谣言的节点对该节点的影响力相同,健康节点接触到谣言信息后会以一定概率转化为知晓节点,则S类节点转化为知晓节点I1的概率P3可表示为:
(5)
由P3定义可知,当M(k)=0时,此时健康节点的邻居节点有可能全部为健康节点,即节点接触不到谣言信息,此时Nk(I1)=0,由公式(5)可知P3≈0,此时节点成为知晓节点的概率基本为0,符合实际情况.
对于知晓节点I1而言,当M(k)>0时,表示邻居节点对知晓节点的影响体现为不相信谣言,则I1类节点转化为免疫节点R的概率P4可表示为:
(6)
实际谣言传播过程中节点对谣言的辨识能力越强,越不容易相信并传播谣言,但当辨识能力强的节点选择相信谣言,相对于辨识能力弱的节点,免疫节点说服辨识能力强的节点使其不再相信谣言的难度较大,从公式(6)可以看出,随着P(k)的增大,I1类节点转化为免疫节点R的概率P4变小.
对于知晓节点I1而言,当M(k)<0时,表示邻居节点对知晓节点的影响体现为相信并传播谣言,则I1类节点转化为传播节点I2的概率P5可表示为:
(7)
对于知晓节点I1而言,当M(k)=0时,表示邻居节中相信并传播谣言的节点与不相信谣言的节点对该节点的影响力相同,则知晓节点保持原来状态不变.
对于传播节点I2而言,由于节点相信并传播谣言,当其邻居节点中存在免疫节点时,I2类节点转化为免疫节点R的概率P6可表示为:
(8)
S2IR谣言传播模型中各类节点状态转化如图1所示.
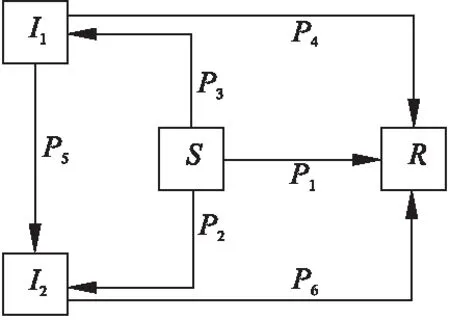
图1 节点状态转化图
图1所示的谣言传播模型的传播规则如下:
1)对于S类节点,当M(k)>0时,以概率P1转化为R类节点,此时P2=0、P3=0;当M(k)<0时,以概率P2转化为I2类节点,此时P1=0、P3=0;当M(k)=0时,以概率P3转化为I1节点,此时P1=0、P2=0;
2)对于I1类节点,当M(k)>0时,以概率P4转化为R类节点,此时P5=0;当M(k)<0时,以概率P5转化为I2类节点,此时P4=0;当M(k)=0时,保持原来状态;
3)对于I2类节点,当M(k)>0时,以概率P6转化为R类节点;当M(k)≤0时,保持原来状态.
由上述谣言传播演化模型可知,网络中任何节点对谣言态度的转变是一个动态过程,谣言传播率呈现一定的非一致性[16],状态转变的概率与节点的所有邻居节点都相关,由于不同类节点在谣言传播过程中对其它节点的影响力不同,加之不同节点的邻居节点中各类节点数目不同,使各类邻居节点对节点影响力的累积效果不同,因此考虑了节点影响力对传播率的影响后,使节点间的谣言传播率具有动态非一致性,很大程度改变了谣言在社交网络中的传播特性,符合社交网络中个体面对谣言时的真实心理状况.
3 理论分析
通过以往的研究,我们发现在线社交网络如Twitter、Live Journal等,不仅具有较高的聚类系数与较小的平均路径长度,网络节点度分布还具有明显的幂律分布特性[17],因此本文利用平均场理论,采用聚类系数可变的无标度网络来研究在考虑了节点影响力的S2IR模型中谣言的传播特性.
t时刻度网络中为度为k的节点中健康节点、知晓节点、传播节点、免疫节点的密度分别用S(k,t)、I1(k,t)、I2(k,t)、R(k,t)表示,由于社交网络中谣言传播具有速度快、时间短的特点,因此本模型假设谣言传播过程中网络中节点数目不变,网络结构不变,故有:
S(k,t)+I1(k,t)+I2(k,t)+R(k,t)=1
(9)
根据谣言传播规则建立均匀场方程如下:
(10)
(11)
(12)
(13)
P(j/k)为网络中节点的度相关性,含义为度为k的节点连接到度为j的节点的条件概率,可表示为[18]:
(14)
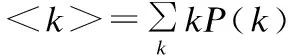
t=0时刻,即谣言传播初始时刻,度为k的节点中健康节点、知晓节点、传播节点、免疫节点的密度满足:S(k,0)≈1,I1(k,0)≈0,I2(k,0)≈0,R(k,0)≈0,对公式(10)积分可得:
(15)
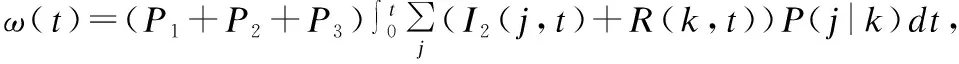
(16)
由谣言传播规则可知,谣言传播会经历传播到消亡的过程,故当谣言传播达到稳定状态时,网络中最终只剩下健康节点与免疫节点,知晓状态与传播状态的节点密度为0,此时有:
<
(17)
谣言传播最终范围可用R(∞)表示为:
(18)
将公式(15)代入公式(18)即可得谣言传播最终范围,节点影响力通过影响P1、P2、P3进而改变S转化为R的概率,最终影响谣言传播最终范围.下面采用实验仿真的方法分析谣言在本模型上的传播特性.
4 仿真结果分析
通过研究我们发现无标度网络节点度虽然服从幂律分布,但聚类系数较小,不能很好地模拟现实社交网络聚类系数较高的实际,为了使仿真结果更贴近实际,本文利用聚类系数可变的无标度网络对谣言在本文所提S2IR模型上的传播特性进行仿真实验.聚类系数可变的无标度网络[19]是由Holme与Kim首先提出的,在经典的BA无标度网络的基础上,在网络的形成过程中引入三角连接概率P来控制网络的聚类系数,网络的聚类系数随P的增大而增大,当P为0时,对应的网络为经典的BA无标度网络.仿真过程中选取CoreTMi5四核处理器,16GB运行内存,Windows 8操作系统,MatlabR2015a为实验平台,按照聚类系数可变的无标度网络生成算法随机生成20个节点数目为5000的无标度网络.假设谣言传播初始时刻网络中只有一个传播谣言,在每个网络上随机选择10个节点作为传播节点,分别进行10独立的谣言传播过程,所有实验结果均为200次独立运行的平均.网络中健康节点、知晓节点、传播节点、免疫节点与网络中节点总数的比值分别用P(S)、P(I1)、P(I2)、P(R)表示.
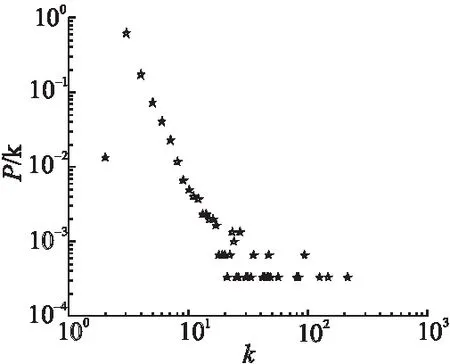
图2 聚类系数可变的无标度网络度分布图
聚类系数可变的无标度网络的节点度分布情况如图2所示,从图中可以看出网络节点度分布具有明显的幂律分布特性,具有无标度网络的特征,该网络的聚类系数为0.5736,与Facebook、Twitter等真实社交网络聚类系数值相差很小,能够很好地满足本模型对仿真网络的要求.
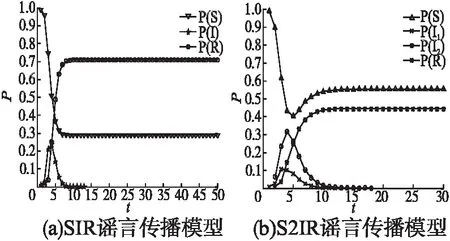
图3 两种模型下的谣言传播图
两种模型下谣言传播情况如图3所示,由于谣言信息具有重要性的特点,本次仿真过程中设定谣言的重要程度I=0.75,谣言所涉及问题的模糊程度A=0.7,由于节点辨识能力与个体自身受教育程度、知识水平以及社会环境有关,不失一般性,令P(K)=0.5.通过对比我们发现,在谣言传播过程中S2IR谣言传播模型感染节点密度大于SIR谣言传播模型感染节点密度,谣言传播最终范围前者为44%,后者达到了70%,这主要因为在谣言传播初始阶段,网络中传播节点数目大于免疫节点数目,节点的邻居节点中传播节点影响力大于免疫节点影响力,节点选择传播谣言的概率随着传播节点数目的增大而增大,相比于SIR谣言传播模型传播率的一致性,S2IR谣言传播模型中谣言传播具有更快的传播速度,谣言传播后期,随着免疫节点数目的增加,邻居节点中免疫节点的影响力大于传播节点的影响力,节点选择不相信谣言的概率增加,在一定程度上减小了谣言传播的范围.通过图3(b)可以看出,在谣言传播初步阶段,知晓节点密度大于传播节点密度,而后随着时间推移,传播节点密度最终大于并一直大于知晓节点密度,这主要因为当一个谣言出现时,个体首先会根据自身辨识能力、社会环境等因素决定是否传播谣言,即先成为知晓节点,而随着谣言传播高潮的到来,节点的邻居节点中传播谣言节点对节点的影响力增大,节点成为传播节点的概率大大增加.相对于SIR谣言传播模型,考虑了节点影响力的S2IR谣言传播模型虽然具有更快的谣言传播速度,但谣言传播最终范围却受到限制.
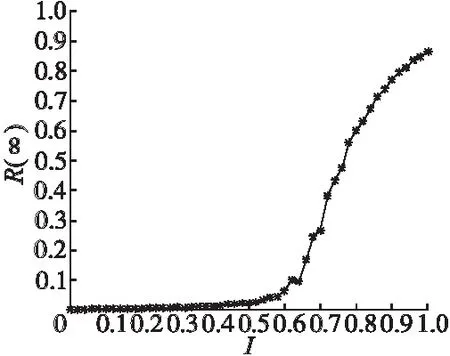
图4 谣言重要程度对谣言传播的影响
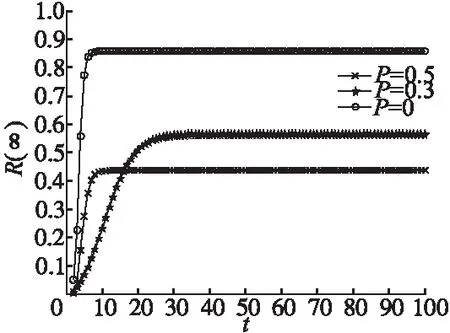
谣言所涉及问题的重要程度对谣言传播的影响如图4所示,由图可知,当0≤I≤0.4时,谣言重要程度的增大对谣言最终传播范围影响不大,当0.4 图5 节点辨识能力对谣言传播的影响 图6 聚类系数对谣言传播的影响 节点辨识能力对谣言传播最终范围影响如图5所示,由图可以看出节点辨识能力对谣言传播范围的影响幅度存在阈值,当节点辨识能力小于0.6时,节点辨识能力的增大对谣言传播最终范围影响较小,当节点辨识能力大于或等于0.6时,节点辨识能力的增大会使谣言传播最终范围大幅度减小,当节点辨识能力等于1时,谣言最终传播范围约为0,意味着谣言此时无法在网络中传播.一般来说,当节点辨识能力较小时,个体对谣言内容的不确定性无法通过自身辨识能力消除,节点辨识能力的增长对节点影响力的影响较小,当节点辨识能力较大时,个体对谣言有了进一步的认识,几乎能辨别谣言信息的真假,此时谣言无法在网络中进行传播. 网络聚类系数对谣言传播特性的影响如图6所示,图中P为三角连接概率,由图6可以看出,在考虑了节点影响力的谣言传播模型中,谣言传播最终范围随聚类系数的增大而减小,当P=0时,对应网络为经典的BA无标度网络,谣言传播最终范围达到最大值.这主要因为网络的聚类系数越低,节点的孤立性越明显,当谣言发生时,邻居节点的影响力对其作用越小,节点往往根据自身对谣言的认识程度选择对谣言的态度,节点极易传播谣言,最终使谣言传播最终范围变大.当P=0.5时,谣言传播最终范围约为43%,这与图3(b)所示谣言传播最终范围大致相同,进一步验证了模型的适用性. 社交网络中节点传播谣言受所有邻居节点共同影响,基于此,本文研究了节点影响力对谣言传播特性的影响,并将节点分为四类,基于平均场理论,使谣言传播率与节点影响力相关,建立了S2IR谣言传播模型,利用聚类系数可变的无标度网络进行仿真实验.结果表明,相对SIR谣言传播模型,S2IR谣言传播模型中谣言具有更快的传播速度和更小的传播范围,节点辨识能力、谣言所涉及问题重要程度以及网络的聚类系数对谣言传播最终范围影响较大.研究过程中,只分析了节点影响力对聚类系数可变的无标度网络谣言传播的影响,真实社交网络中考虑节点影响力对谣言传播的影响是下一步研究的重点.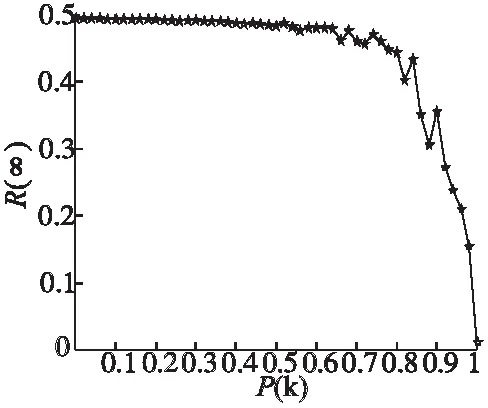
5 结 语

