基于TVAC-PSO算法的可重构微电网优化调度方案
吴成明, 尚锦萍, 吴婷婷, 杨 逸, 张 杰
(三峡大学 电气与新能源学院,湖北 宜昌 443002)
0 引言
微电网是一种小规模的电力系统,由各种分布式能源、储能系统和不同类型的负荷(可控负荷或固定负荷)组成,既可以在电网上运行,也可以在孤岛模式下运行[1~4]。由于可再生能源的发展以及电力市场的倾向,微电网的不确定性逐渐成为人们关注的主要问题之一[5]。
目前国内外在微电网不确定性和微电网经济性优化调度领域的相关技术研究已逐步开展。文献[6]提出一种具有可调度能力的微电网优化运行实时控制策略,并建立了一种SA评估模型,提高了电网供需两侧的经济性。文献[7]综合考虑“源储荷”协调调控,提出一种广义能量优化鲁棒模型,增强了系统调度的灵活性。文献[8]使用云滴模拟多不确定性问题,将不确定性的模糊性和随机性的定性分析转化为定量分析。文献[9,10]考虑RES出力的不确定性,以微电网经济性最优为目标建立混合整数规划的两层随机调度模型。文献[11]利用模型预测控制实现日内滚动优化,并引入可调容量比例因子,可以实现功率跟踪,增强微电网的调度响应能力。为提高微电网运行的可靠性,文献[12~14]分别提出贝叶斯—粒子群优化算法,一种随机最优临近粒子群算法和量子粒子群算法,均提高了寻找微电网优化问题最优解的收敛速度和运算效果。
综合以上分析,本文提出一种基于TVAC-PSO算法的RSMG优化调度方案。该方案以微电网利润最大化为目标,将风速、销售和购买价格作为不确定参数,采用情景生成法来模拟这些参数,运用TVAC-PSO算法找出每小时最优的微电网配置。根据微电网的成本,收益以及风险评估,确定微电网的利润,并通过一个10节点的微电网模型验证了本方案的可行性。
1 基本模型
1.1 目标函数
微电网具有不同的成本和收益类型,以微电网利润最大化为目标,通过考虑总收益和总成本的差异,得出微电网的总利润。因此,在重组过程中优化调度的目标函数如下:
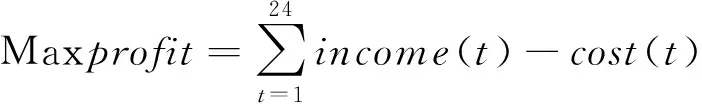
(1)
其中:income(t)表示总收入;cost(t)表示总成本。
1.2 成本定义
总成本由4部分组成:
(2)
其中:cost1表示调度单元运行成本;cost2表示转换成本;cost3表示从主电网购买电力的成本;cost4表示不提供能源时的成本。
1)调度机组运行成本
调度机组运行成本由发电成本、启动成本和关机成本3部分组成,本文采用分段线性模型表示发电成本,具体如下:
(3)
式中:Ng表示调度机组的编号;Pi表示第i个可调度单元的运行成本;Ui表示第i个可调度单元的启动成本;Di表示第i个可调度单元的关闭成本。
2)转换成本
每个开关的状态由开(0)和关(1)两种状态组成。每次开关的状态转换都有一个操作成本。因此,根据开关动作的次数,转换成本的公式如下:
ϑSNS(t)
(4)
式中:S表示开关的编号;N表示开关操作的次数;ϑ表示开关操作的成本。
3)购电成本
在某些时间内,分布式电源不能满足供电需求。因此,必须从主网购电。购电成本公式如下:
(5)
考虑到不同时段购电价格的不同,这里采用ARMA模型定义购电价格γ(ωi),表示在不同购电方案ωi(ω1,…,ωN)下的购电价格。具体定义如下:
(6)
其中,ξ1表示购电的时间点。每一个γ(ωi)都可以和一个概率π(ω)相关联,其可以被定义为:
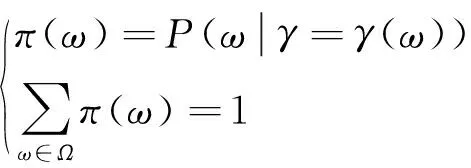
(7)
4)不提供能源时的成本
考虑能源供应不足时对系统可靠性的影响,将其折算为具体的成本:
(8)

1.3 收益定义
总收益包含两个部分:
(9)
式中:Income1向主网售电的收入;Income2表示向负荷供电的收入。
1)向主网售电的收入
这里假定出售给主网的剩余电力通常是由风能等可再生能源生产的,因此,作为一种更多利用风能的方案,在一天的时间里,销售价格都比购买价高。向主网售电的收入如下:
(10)
同公式(6),这里τ(t)定义为:
(11)
每一个η(ωi)都可以和一个概率π(ω)相关联,其可以被定义为:
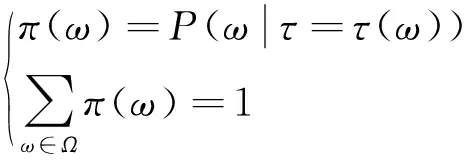
(12)
2)向负荷供电的收入
不同类型负荷的供电收入如下:
(13)
式中:σ表示供电的价格;P3表示供电量。
1.4 风机出力模型
风力是风力发电不确定性的主要原因之一。风力发电机的发电功率取决于日风速。假设风速由不同场景产生,则用V(ω)表示,可定义为以下矩阵:
(14)
这里,VωNNT表示在场景ωN和时间NT下的风速。
每一个ω都可以和一个概率π(ω)相关联,其可以被定义为:
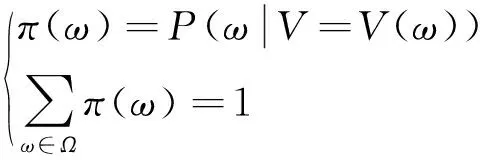
(15)
根据每种情况下的风速V(ω)计算风力涡轮机产生的功率如下:
(16)
0≤V≤Vcut-in
Vcut-in≤V≤Vrated
其中,
Vrated≤V≤Vcut-out
Vcut-out≤V
定义风力机输出功率的参数如表1所示。

表1 风机特性
1.5 约束条件
1) 功率平衡约束
风电机组的发电量与主网之间的功率交换和负荷需求,必须始终满足功率平衡约束:
(17)
式中:Pg,i(t)表示发电机产生的功率;Pw(t)表示可调度的功率;Pq(t)表示与电网交换的功率;Pc(t)表示损失的功率;Pl,j(t)表示负荷功率。
2)最大和最小发电约束
(18)
3)机组爬坡率约束
(19)
4)节点电压约束
(20)
5)支路电流限制
(21)
定义发电机输出功率的参数如表2所示。

表2 发电机特性
2 改进算法研究
2.1 模型改进
1)风险规避与风险度量
本文引入期望效用原理,在原有模型的基础上增加对微电网调度风险问题的考虑,提出了随机重构问题风险约束模型的一般形式:
(1-μ)EU+μη
(22)
式中:μ∈{0,1}表示一个权重,用于实现风险规避与预期利润之间的交换。η是重构问题的一种风险度量标准。为了度量风险,本文采用了条件风险值(CVaR)作为风险度量,根据利润分布,CVaR定义为:
CVaR(ε,x)=
(23)
使用一个约束来计算CVaR:
η-EUω≤Sω≥0
(24)
式中:EUω为第ω套方案的期望效用;Sω为连续非负变量;η为辅助变量。
2)带有风险评估的目标函数
根据公式(22)~(24)中提出的基于CVaR的风险评估模型,将公式(1)中的最优调度的目标函数改写为:
(25)
这里,Yt,ω表示在t时刻,ω场景下微电网的拓扑结构,但需要符合功率平衡约束。
(26)
除上述约束外,还增加了以下两个新的约束用于计算CVaR。
(27)
2.2 算法改进
如前所述,为了模拟不确定参数并找到最佳配置,分别运用场景生成法和TVAC-PSO算法,描述ARMA模型和TVAC-PSO的场景生成过程。
2.2.1 情景生成过程
在与连续随机变量相关的随机规划中,使用有限的一组值来找寻最优解是十分困难的。为了找到随机变量的适当值,采用基于ARMA模型的情景生成。基于ARMA模型下随机变量y在情景生成中的一般形式如下:
(28)
式中:φj和θj是自回归和滑动参数;εt和εt-j是白噪声误差项。
假设想在NT小时内生成NΩ场景。根据公式(28),第一小时(y11)的第一种情况计算如下:
y11=φ1y0+ε0-θ1ε1
(29)
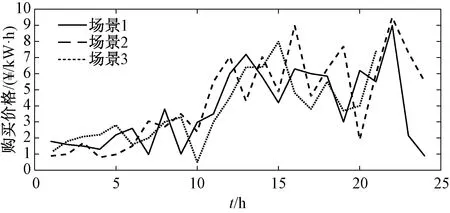
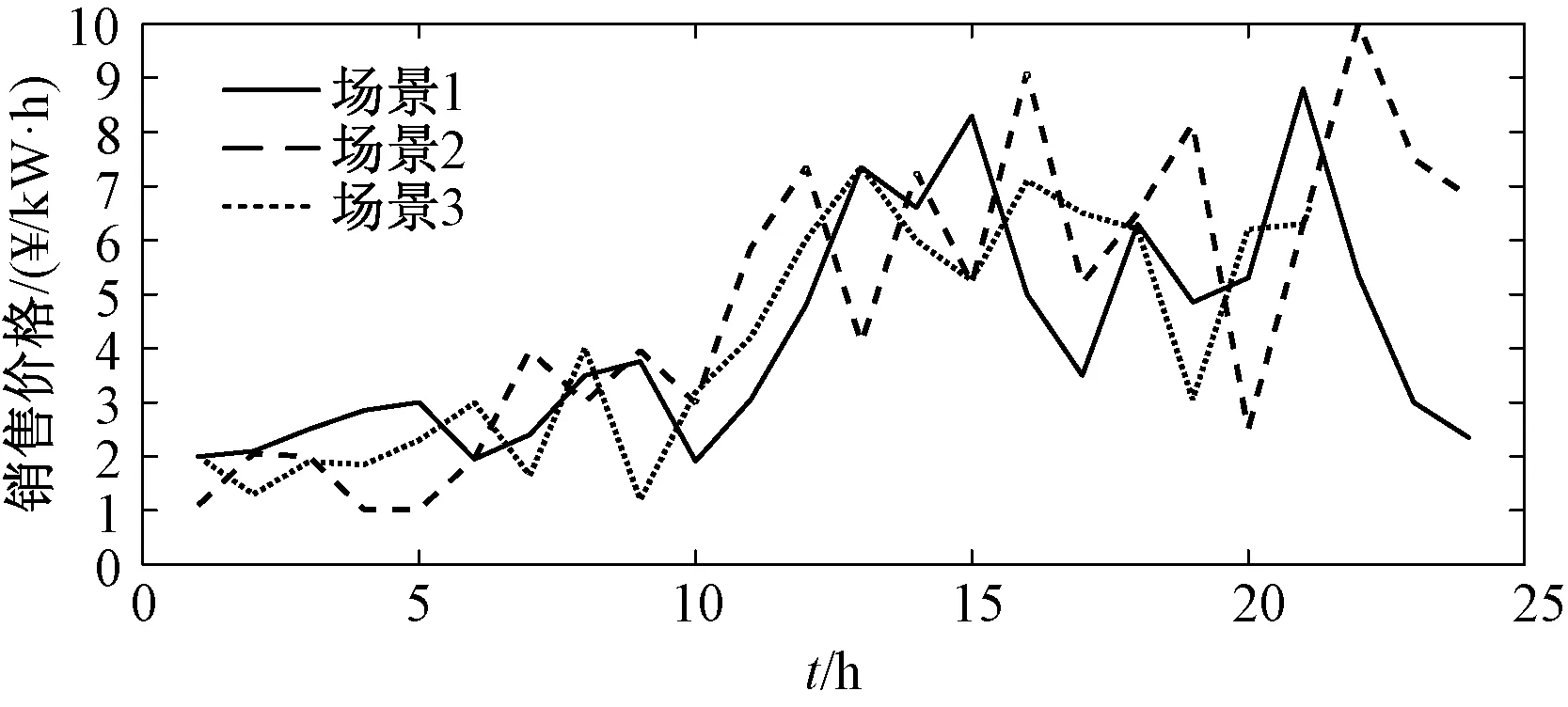
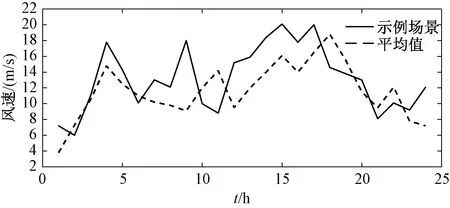
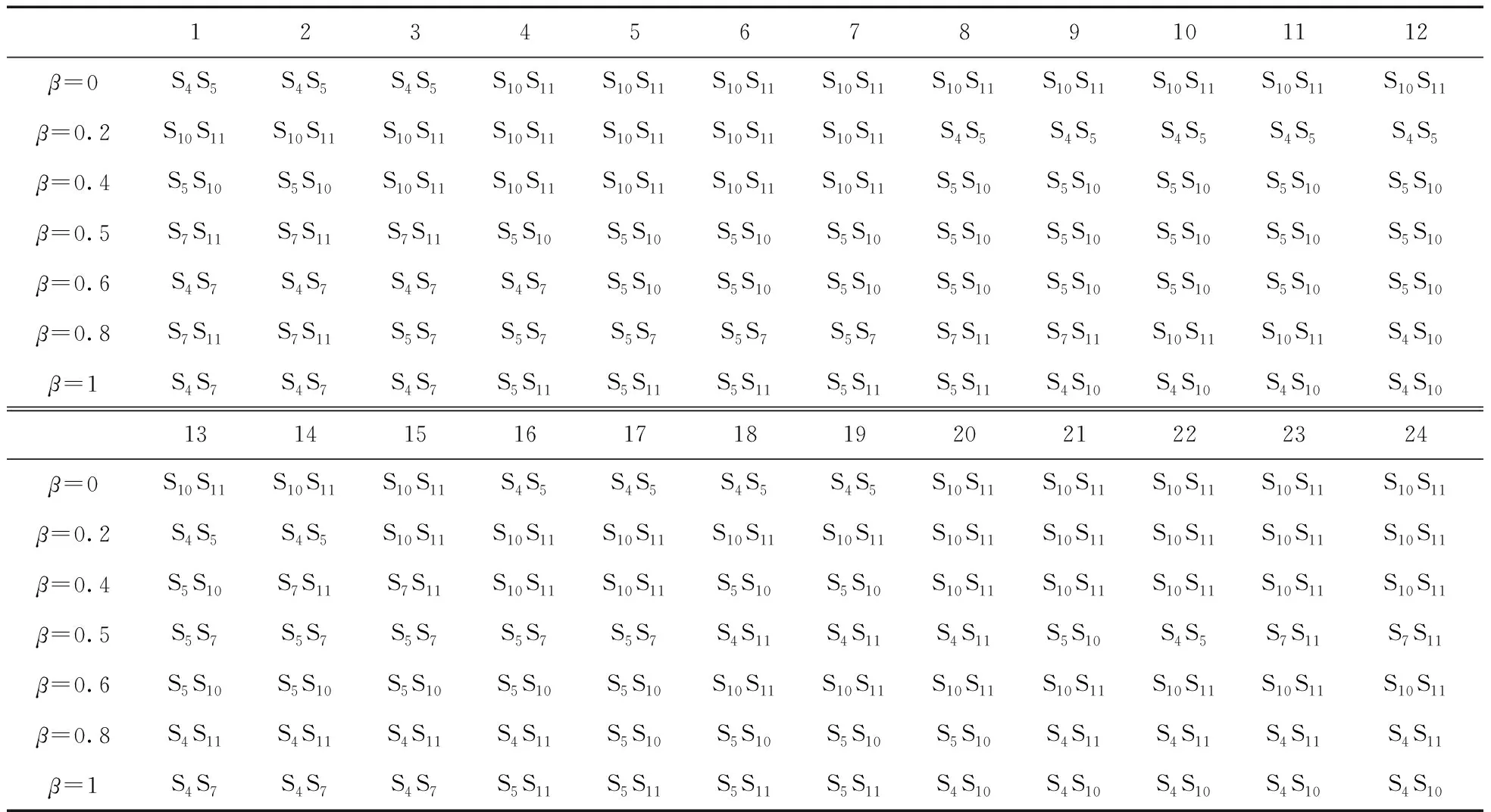
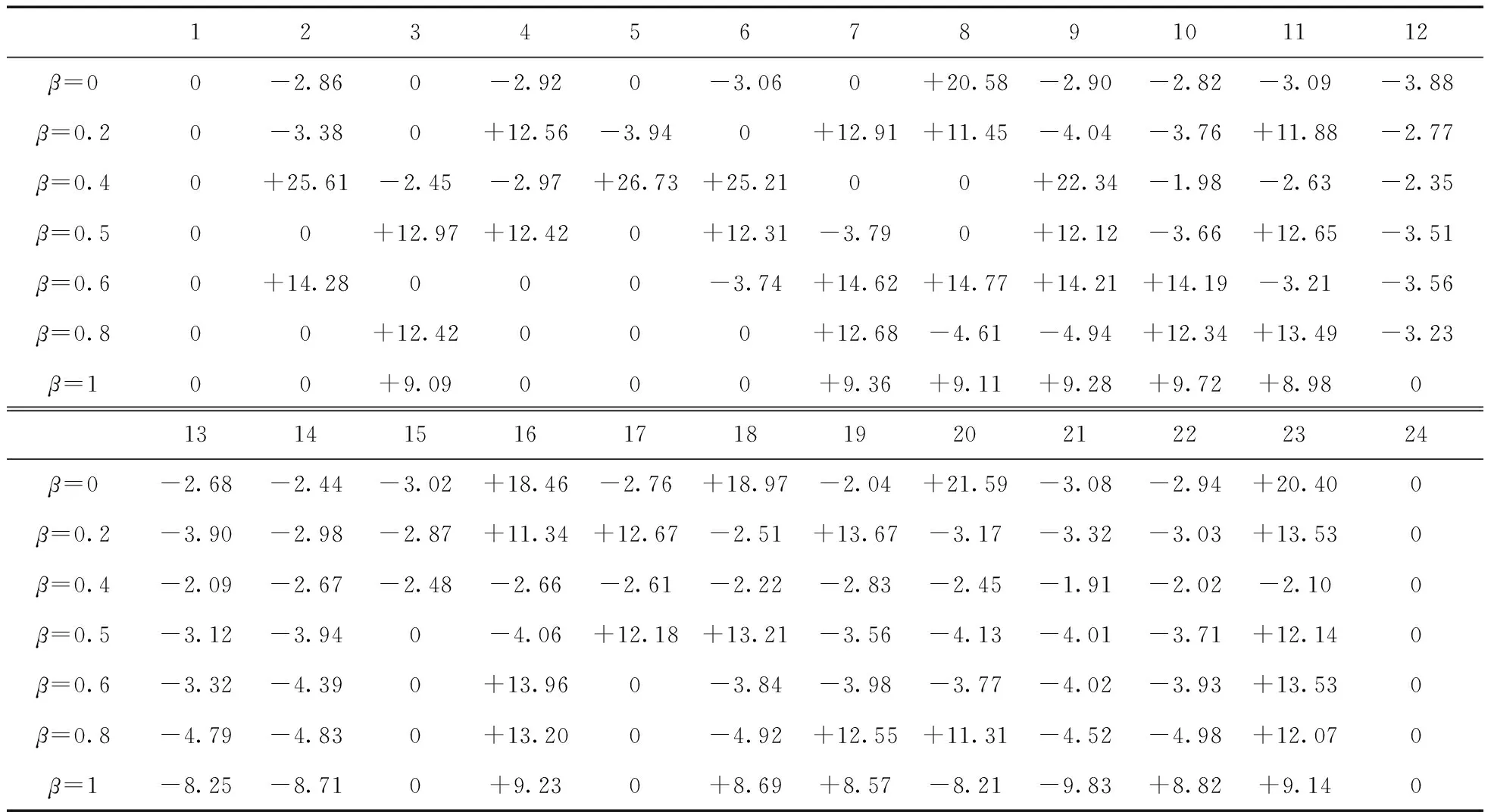
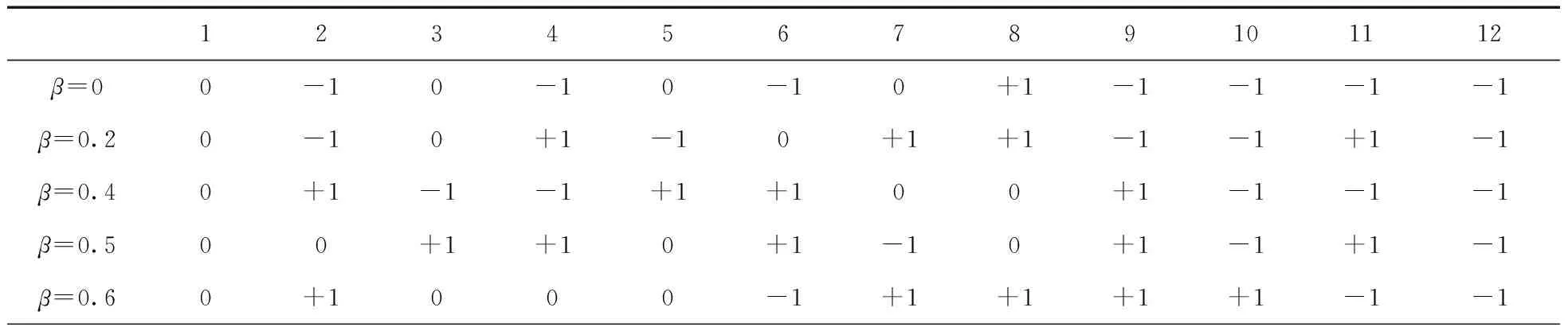
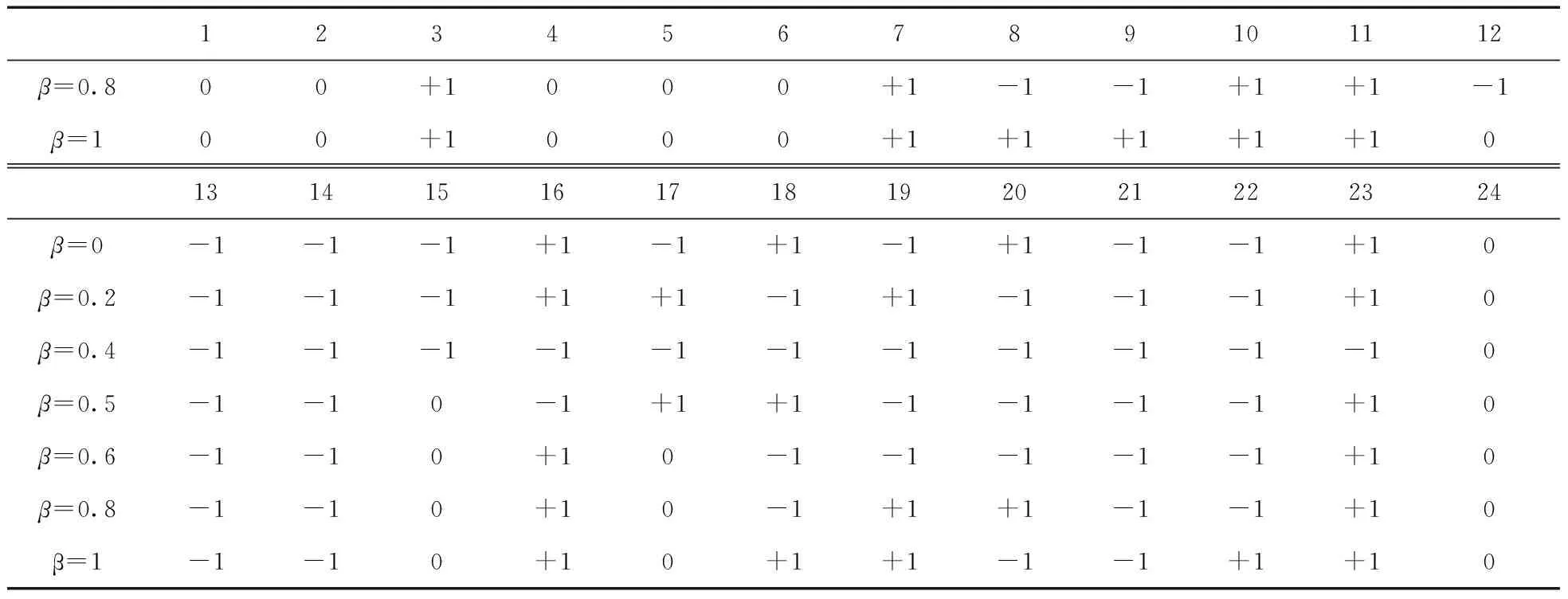
ARMA参数(φ1,θ1)是基于观察值与ARMA模型的值之间的最小化误差。这可以通过使用ARMAX函数在MATLAB中完成。白噪声(ε0,ε1,…,εN)是从均值为零的正态分布εt~(0,σ)中随机生成的,以此确定y11。重复以上过程直到NT>t。将第一个场景时间全部设置为NT,令ω←ω+1,直到ω 2.2.2 随时间变化的加速度系数粒子群算法(TVAC-PSO) 粒子群算法(PSO)操作简单、容易理解,广泛运用于动态经济调度中,但其收敛速度慢,易陷入局部最优[15]。本文研究的是在收敛时间较短的情况下的微电网重构问题,因此提出了具有时变加速系数(TVAC)的粒子群优化算法来寻找最优解。在传统的PSO中,每个粒子以指定的速度向最佳位置移动。第j粒子的新速度和位置如下表述[12]: (30) 式中:xj(t)和Vj(t)分别为第j个粒子的初始位置和速度;xj(t+1)和Vj(t+1)分别为第j个粒子的新位置和速度。Pbest是由第j个粒子获得的适应度函数的最佳值(局部解);Gbest是到目前为止由任意粒子获得的适应度函数的最佳值(全局解)。惯性权重ω如下: (31) 式中:Itermax是最大迭代次数;Iter是当前迭代次数;ωmin,ωmax是最小和最大惯性权重。PSO寻找更准确和更有效最优解的重要方法是参数调整。它通过改变加速度系数(C1和C2)来实现的,而外部加速系数则随着搜索的进行而增加。在TVAC-PSO算法中,加速度系数C1和C2表示为: (32) 式中:c1f,c1i和c2f,c2i分别是内部和外部的加速系数。 在10节点RSMG系统中进行仿真,验证本文提出的算法。在该系统中,通过使用场景生成法,对不确定参数进行建模。由上文可知,β是用于权衡风险规避和预期利润的加权参数,因此,本节将在系统中对不同的β值用MATLAB软件进行仿真,并作出风险分析。 图1 10节点RSMG系统结构 10节点RSMG系统结构如图1。该系统包括3个可调度发电机,风力发电机组,8个负载和11个开关。根据上文提出的约束,系统在任何时候都应该打开两个开关。 表3为10节点微电网系统的线路数据(标幺值)。日均负荷需求和电价曲线如图2所示。 表3 10节点微电网系统的线路数据 图2 10节点RSMG日负荷需求和电价曲线 根据该算法,购销电价格和风速由不同的场景生成,并将其作为不确定性的参数。作为奖励方案,销售电力的价格始终大于购买的价格,购买和销售电力情景的一些样本如图3,图4所示。图5表示一天中每个小时的风速场景平均值,并根据β∈{0,0.2,0.4,0.5,0.6,0.8,1}的不同取值,TVAC-PSO算法可以找到每个小时的最优配置。 图3 10节点系统每小时购买电价的场景 图4 10节点系统每小时销售电价的场景 图5 10节点系统风速样本情景和24 h场景平均值 表4是RSMG系统开关重新配置的最佳结果。在表4中,根据β的值可以得到每一小时的开关状态。在找到RSMG的最佳拓扑结构后,便可得到每小时RSMG系统与上级电网之间功率分配关系,如表5所示。 由表5可知,当β=0时,第2个小时的功率分配情况为主电网向RSMG系统输送2.86 kW的功率,第3个小时的功率分配情况为主电网与RSMG系统之间无功率交换,第8个小时的功率分配情况为RSMG系统向主电网输送20.58 kW的功率。限于文章篇幅,在此便不再一一叙述主电网与RSMG系统之间的功率分配情况。表6是根据表5的功率分配结果所得到的,表示了基于不同β值的功率交换结果,其中,销售,购买和非交换模式分别用+1,-1和0表示。 以上可以看出,通过增加β值,RSMG系统可以在一天中的更多时间向上级电网销售电能。 在本文中设定ε=0.95,因此风险度量CVaR1-ε=CVaR0.05。 表7给出了不同β值下最优调度问题的预期利润。可以看出,在β值较小时,系统是低利润高风险;增加β值,系统预期利润增加,风险降低。例如,当β=0和β=1,系统预期利润是154.76元,165.90元,β=0和β=1时的风险损失分别是130.48元,103.56元。通过从0到1的增加β值,预期利润增加了11.14元。对于不同的β值,预期利润和风险损失的变化如图6所示。 表4 每小时RSMG系统在不同β值下重新配置结果 表5 RSMG系统与上级电网之间功率分配情况 表6 RSMG系统与上级电网之功率交换情况 续表6 表7 RSMG中不同β值的最优调度结果 图6 RSMG中不同β值下最优调度结果的关系 表7给出了不同的β取值下RSMG的预期利润与风险损失之间的关系,当β取值由0不断增加到1时,其对应的利润与损失之间的数量差也是逐渐增加,说明β取值越大,其对应的预期利润越大,风险损失越小。而本文所提的RSMG调度方案就是为了使整个系统尽可能地处于一个高利润低损失的状态。由此可知,当β取值为1时,RSMG系统的调度方案是一个最优调度方案。 本文研究了RSMG系统的风险优化调度,使微电网系统利润最大化。为此设计了具有风速和市场价格不确定性的RSMG系统最优调度方案。基于ARMA模型生成情景模拟风速、销售和购买价格的不确定性,通过TVAC-PSO算法得到RSMG的每小时最优配置。本文采用两阶段随机规划问题,对不同的β值制定了最优调度问题的风险度量,并计算了每个情景下的预期利润。仿真结果验证了基于TVAC-PSO算法的风险优化调度方案的有效性,同时在风险度量下的RSMG系统可以在一天中的较长时间内向上级电网销售电能,并获得更大的利益。3 基于TVAC-PSO的CVaR求解流程
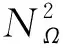
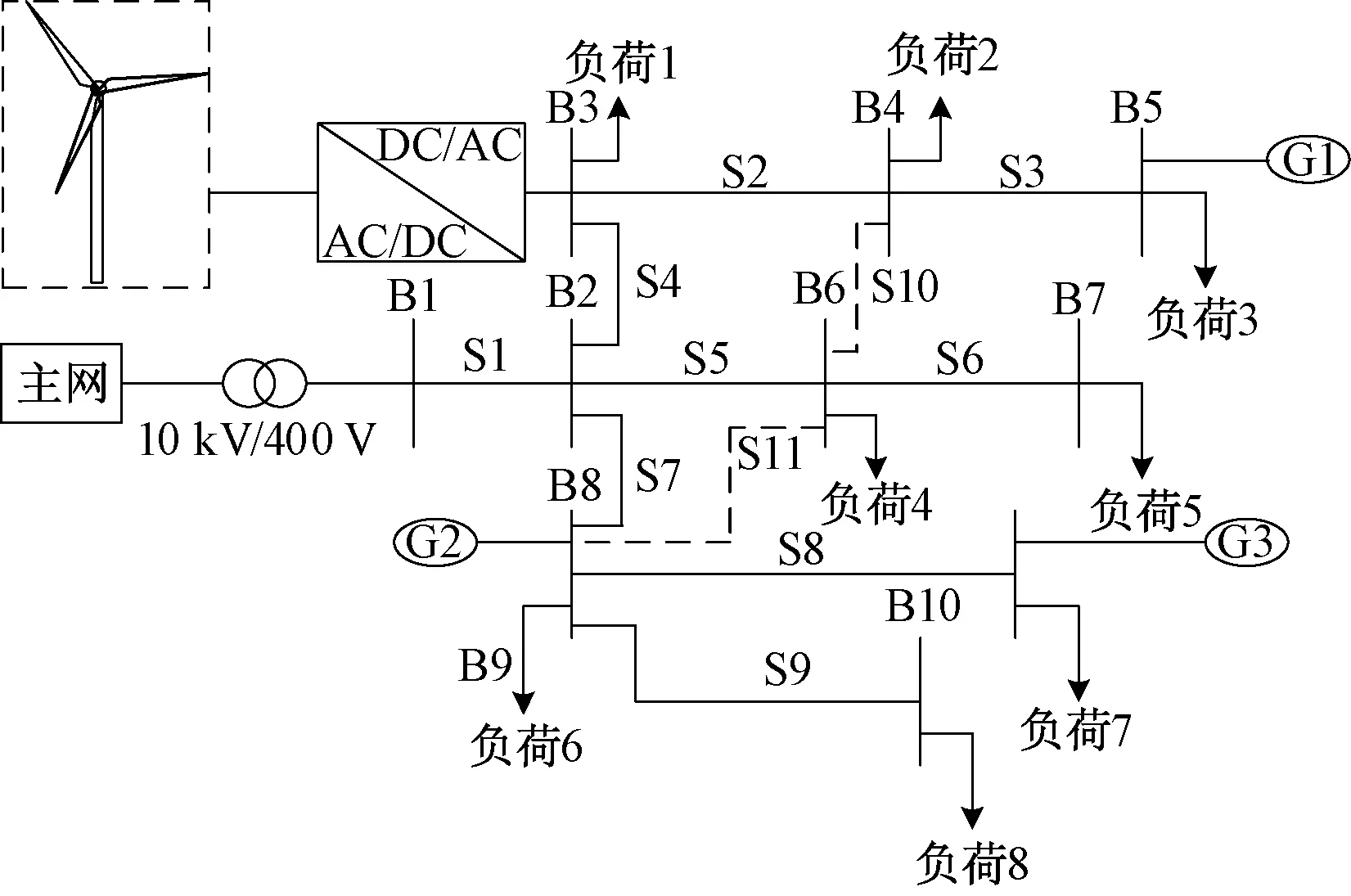
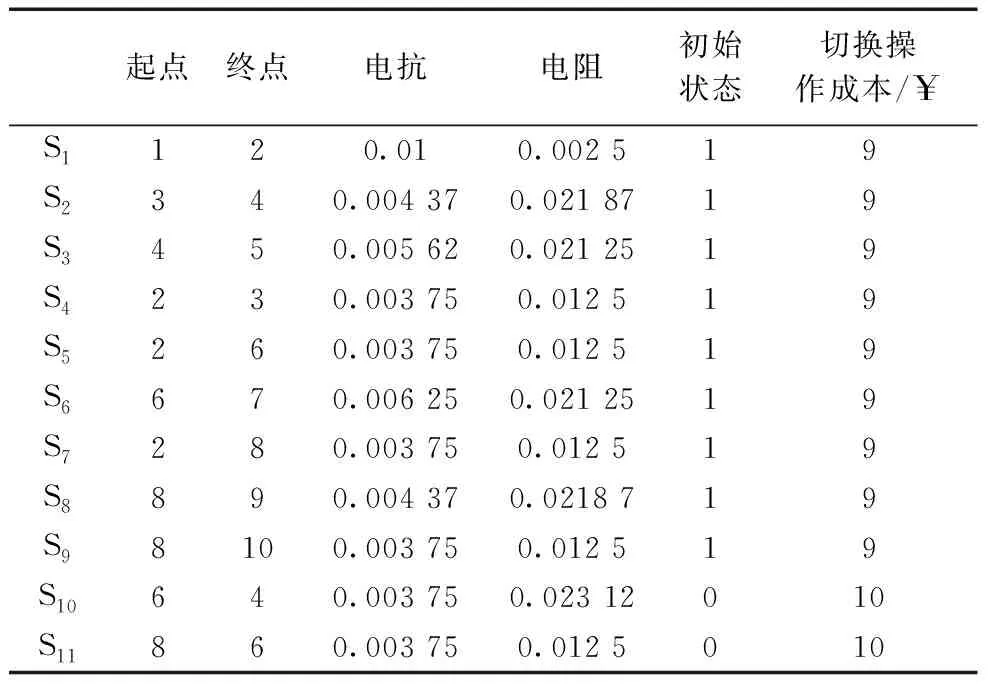
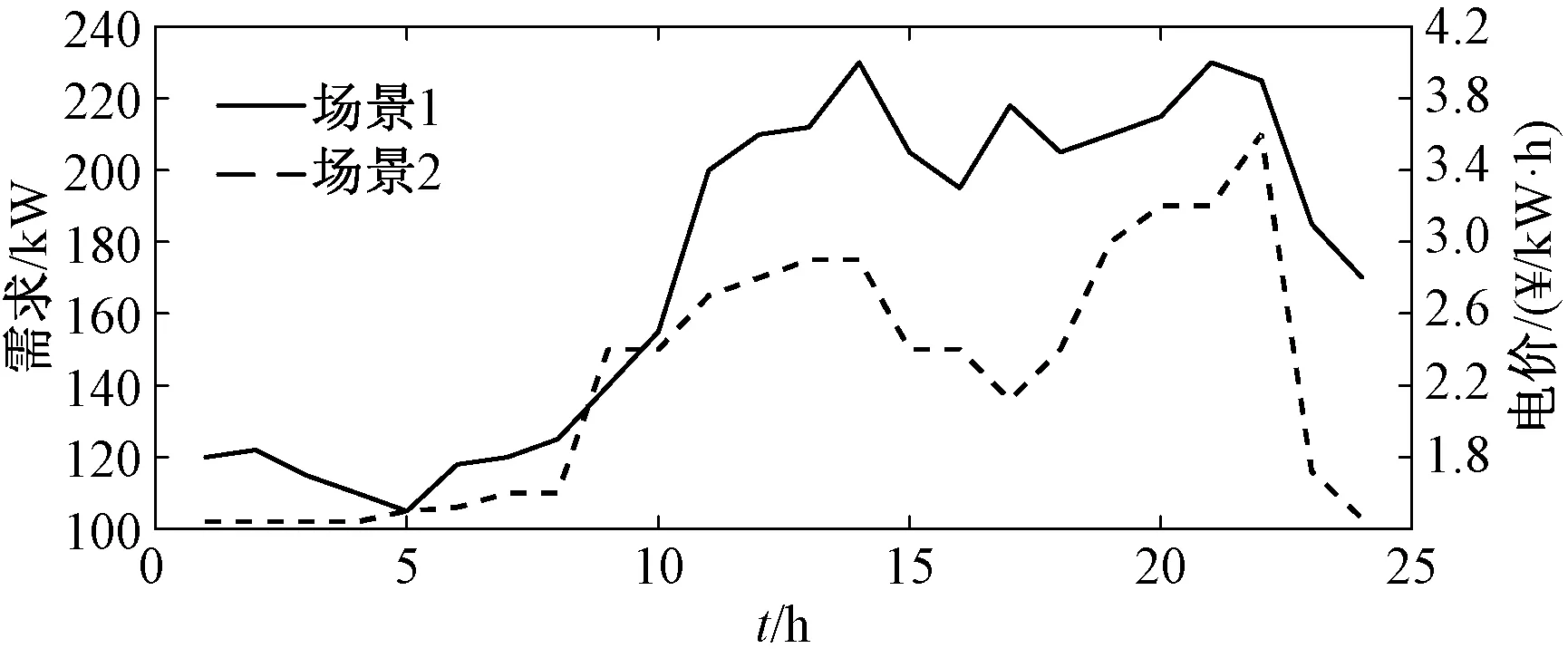
4 算例分析


5 结论

