数学建模思想与方法融入高等数学课程研究
黄娟霞
(陇南师范高等专科学校 数信学院,甘肃 陇南 742500)
高等数学是高等院校理工科专业极为重要的一门基础课程.传统的高等数学课程过于重视理论系统的完善性,忽略数学概念,因此,把数学建模的思想与方法融入高等数学课程,刻不容缓.数学模型就是针对特定现象,借助数学语言对其展开抽象化与简化的描述,方便人们进一步认知所分析的对象.组织构建适用于数学关系问题的数学模型,这种方法便是数学建模[1].在高数课程中引进数学建模的思维和方式,不但可以调动学生的学习兴趣,而且还有助于培育他们运用数学的技能.
1 高等数学教学中融入数学建模的思想与方法
1.1 在概念中渗透数学建模的思想与方法
高等数学拥有缜密的逻辑性、高度的抽象性以及强大的应用性.以定积分为例,在讲解定积分的概念时,首先引入“曲边梯形的面积和变力沿直线作功”这两个问题[2],而这两个问题的解决过程就是一个建模过程,解决方法都经历了“分割(即化整为零)→近似(以常代变)→求和(积零为整)→取极限(无限逼近)”[3]这四步,而定积分的概念恰恰由这四步构成,因此,只需抓住它们的共性,便可引导学生自己阐述定积分的概念.
1.2 在定理的应用中深化数学建模的思想与方法
高等数学的逻辑性体现在定理及其证明上.一直以来定理及其证明是高等数学中的一大难题,学生觉得在实际生活中无法获得验证,没有办法利用数学思维来考虑.因此,在实际中应用数学建模,不仅能提高学生学习的兴趣,而且也能加深对知识的理解.
假设某人以本金A0进行一项投资,投资的年利率为r,求t年后的资金总额.
若以年为单位计算复利(即每年计息一次,并把利息加入下一年的本金,重复计息),则t年后,资金总额将变为A0(1+r)t(元);
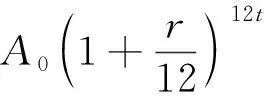


现在让n→∞,即每时每刻计算复利(称为连续复利),则t年后资金总额将变为
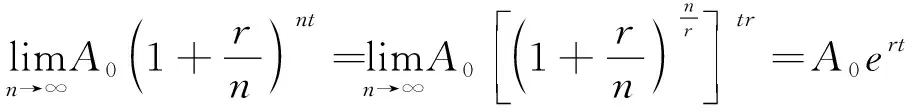
1.3 在课后习题中体验数学建模的思想与方法[3]
从理解知识方面来看,利用解题可以全方位把握知识的定义与不同知识间的关联;从培养能力来说,解题是培养学生数学才能和学会思考的一种手段和途径.因此,任课老师在课后给学生留一些习题,让学生进一步体验数学建模的思想与方法,这样既可以巩固所学知识,还可以增加学生的创新意识和创新能力.在学习了函数的极限、导数以及最大值最小值的概念以后,可以让学生体验“不允许缺货的库存管理问题” 的模型建立过程.
问题:为了实现某项生产任务,公司要按时对不同材料进行购置,放置在仓库中待用.
为方便叙述,假设将天作为时间单位,将吨作为货物单位,间隔T天采购一次(T叫作定货周期),单次货物订购量是Q,单次订购费用是c1,每日每吨的保管费用是c2,每日货物需要r吨.而订货量Q,定货周期T以及需求量r之间符合Q=Tr.
在订购以后,库存量从最高值Q均匀减少,设库存量在t时刻是q,则q是时间t的函数,记为q=q(t),其改变规律见图1.
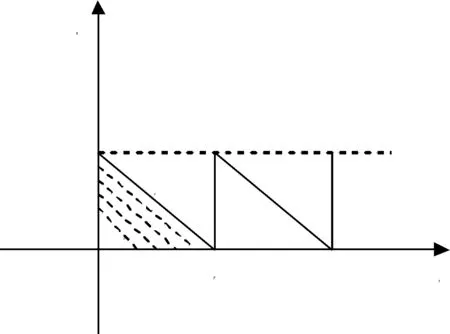
图1 库存量变化图
1.4 探索新的教学模式,改进教学方法[4]
传统的高等数学课程强调连续性和确定性,数学教师一般都采用“满堂灌”、“填鸭式”的教学方法,严重影响学生学习的积极性.为了改变这一现状,我们将数学建模的思想与方法融入高等数学教学课程,采用启发式和讨论式教学方法,即在教学中以学生为主体,教师为主导,教师根据不同情况设置实例、创设情景,突出问题,使数学富于情趣,而且师生共同参与,根据创设的情景,让学生亲历知识的产生过程.
1.5 鼓励学生参加数学建模竞赛
大学生数学建模竞赛最早于1994年由国家教委倡导,我校从 2003 年开始组织学生参加高教社杯全国大学生数学建模竞赛,并多次获得国家级及省级奖励,参赛学生在数学知识的应用方面有了一个跳跃式的提高.但以前的参赛队员仅限于数学各专业学生,课题组一直致力于把数学建模的思想与方法融入高等数学课程的研究中,鼓励其他专业的学生参加比赛,从去年开始,其他各专业学生也开始参与数学建模竞赛,并取得了优异的成绩.
2 结语
课题组把数学建模的思想与方法融入到高等数学课程中,打破了以往“概念——定理——证明——例题——习题”的这种传统教学模式,有助于对学生的运算、空间思维以及逻辑能力等的培养,为我校在数学建模竞赛中取得优异的成绩奠定基础.

