基于向位妨碍的约束状态图模型及其拆卸序列

陈 建 王建勇 黄 林 李锦春

浙江工业大学特种装备制造与先进加工技术教育部/浙江省重点实验室，杭州, 310014

0 引言

实现废旧产品的拆卸处理可有效提高资源利用率、减少环境污染，也是提高企业社会效益和经济利益的重要手段。目前围绕废旧产品的拆卸建模研究大多是将几种基本图模型集成在一起或结合其他理论方法进行建模与拆卸信息表达，这种混合形式图模型较好地解决了单一模型所产生的问题，是拆卸模型构建的重要发展方向。张秀芬等[1]在无向图的基础上，提出了产品拆卸多约束图，增加了拆卸优先级约束和空间约束信息。TAN等[2]构建了信息建模(BIM)技术和改进算法，为拆卸石油平台提供了精确的组件信息。汪开普等[3]针对实际拆卸作业的复杂性，建立了考虑模糊作业时间平衡问题的数学模型，并提出一种基于Pareto解集的多目标遗传模拟退火算法进行求解。JIAO等[4]建立了以评估拆卸序列质量为目标的健身功能模型(FFM)，并提出一种离散BA方法优化拆卸序列问题。宋守许等[5]在构建混合图拆卸模型基础上，将产品拆卸序列转化为一类约束满足问题。LI等[6]为了获得拆卸序列最优解，提出一种拆卸序列规划(DSP)转换为基于拆卸约束图的约束分类问题(CSP)模型方法，并得到有效的可行拆卸序列。REN等[7]为了解决平行拆卸序列(PDP)问题，提出了拆卸过程中的优先约束模型和可视化表示方法。王淑旺等[8]针对拆卸中的不确定问题，构建了拆卸约束混合图拆卸模型。ZHENG等[9]提出一种基于映射关系的OWL动态建模方法，以提高机器人的分解能力。ZHANG等[10]针对平行拆卸问题，构建了基于模糊时间的调度拆卸过程模型。MITROUCHEV 等[11]根据零部件移除轨迹定义了零件之间的约束范围，依据约束方向范围的大小来判断该零部件是否可拆。宋小文等[12]针对由于零件缺陷产生不可拆问题构建了一种五元组拆卸混合图模型，用于表达拆卸组件单元、方向性约束、空间约束、选择性约束和无方向性约束关系。KANG等[13]构建了一种d-BOM结构图模型，根节点表示待拆卸产品整体，叶节点表示不可继续分离部分。李方义等[14]针对目标拆卸问题，提出了一个基于约束和产品拓扑关系的复合有向图模型。江吉彬等[15]针对拆卸设计理论演算多、实用化难等问题，提出面向拆卸对象的层次网络图模型。ZHANG 等[16]通过建立混合模糊模型，提高了拆卸路径规划的环境适应性。李世停等[17]提出了基于约束关系的Petri网拆卸模型，有效地对设备拆卸过程进行了表达。ZHU等[18]采用标准建模语言(UML)方法构建了一种动态拆卸信息模型图，用来表达拆卸方向、空间约束和拆卸工具。邹宾森等[19]针对拆卸线单边不足问题，建立了多目标拆卸性平衡问题模型，并提出一种Pareto蝙蝠算法以提高效率。张雷等[20]为了研究复杂产品的并行拆卸构建了一种混合图，无向边表示零件之间存在某种连接的约束，有向边表示干涉关系。

综上所述，在可拆卸问题研究中，影响拆卸的因素有零件本身的特性(尺寸、质量、结构类型)、约束类型、拆卸工具等，而本文研究的三维向位妨碍是约束类型中的重要影响因素。在拆卸约束问题研究中，零部件可拆是整个拆卸的基础，对可拆卸性的研究若以二维拆卸方向为基础，不研究三维拆卸约束的表示和约束量值的计算，则容易忽略拆卸零件本身空间特性影响，因此，本文在分析机械产品零部件之间装配方式和约束关系的基础上，提出三维向位妨碍的概念和妨碍区间的计算方法，同时根据要拆卸的不同约束情况对计算方法进行优化。

1 向位妨碍约束状态图模型

1.1 三维向位妨碍区间

定义1 在拆卸空间中，任一零部件i的拆卸方向为从零部件i中心发射的无数条射线Sni，如果存在零部件j对零部件i的拆卸移动方向产生阻碍，则称这种阻碍为零部件j对零部件i的向位妨碍，射线Sni形成的封闭曲线S1为可拆卸空间与不可拆卸空间的分界线，具体见图1。

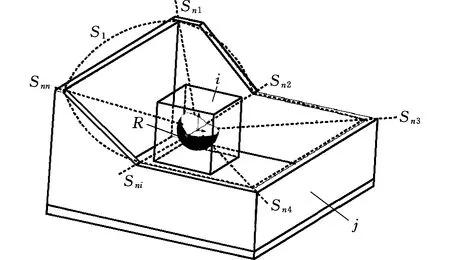
图1 三维向位妨碍示意图Fig.1 3D phase hinder diagram

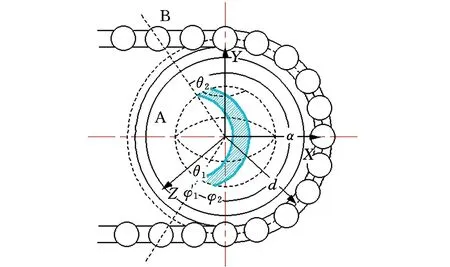
定义2 假设任一零部件j对零件i的向位妨碍射线形成一个三维锥体空间，其顶角用Ω表示，那么总会存在一个半径为r的球体与之相交得到一个妨碍曲面，则称该三维锥体与球体的相交面为三维向位妨碍区间Rij，它的数值大小为球面(r=1)被妨碍射线组成的锥体所截得的球面面积Rij，其中球体中心为妨碍射线汇集点，为零部件i的形心，具体见图2。

图2 三维向位妨碍区间Fig.2 3D phase hinder interval

取笛卡儿坐标系为参考坐标系，那么在向位妨碍球表面上总存在一微小曲面dA，不计高阶无穷小，可把这个微小曲面看成一个长方形，其经线方向的长度dl1=rdθ(dθ为dl1对应的圆心角)，纬线方向的宽度dl2=rsinθdφ(dφ为dl2对应的圆心角)。可得出曲面上面积微元dA=dl1dl2=r2sinθdθdφ，具体见图3。

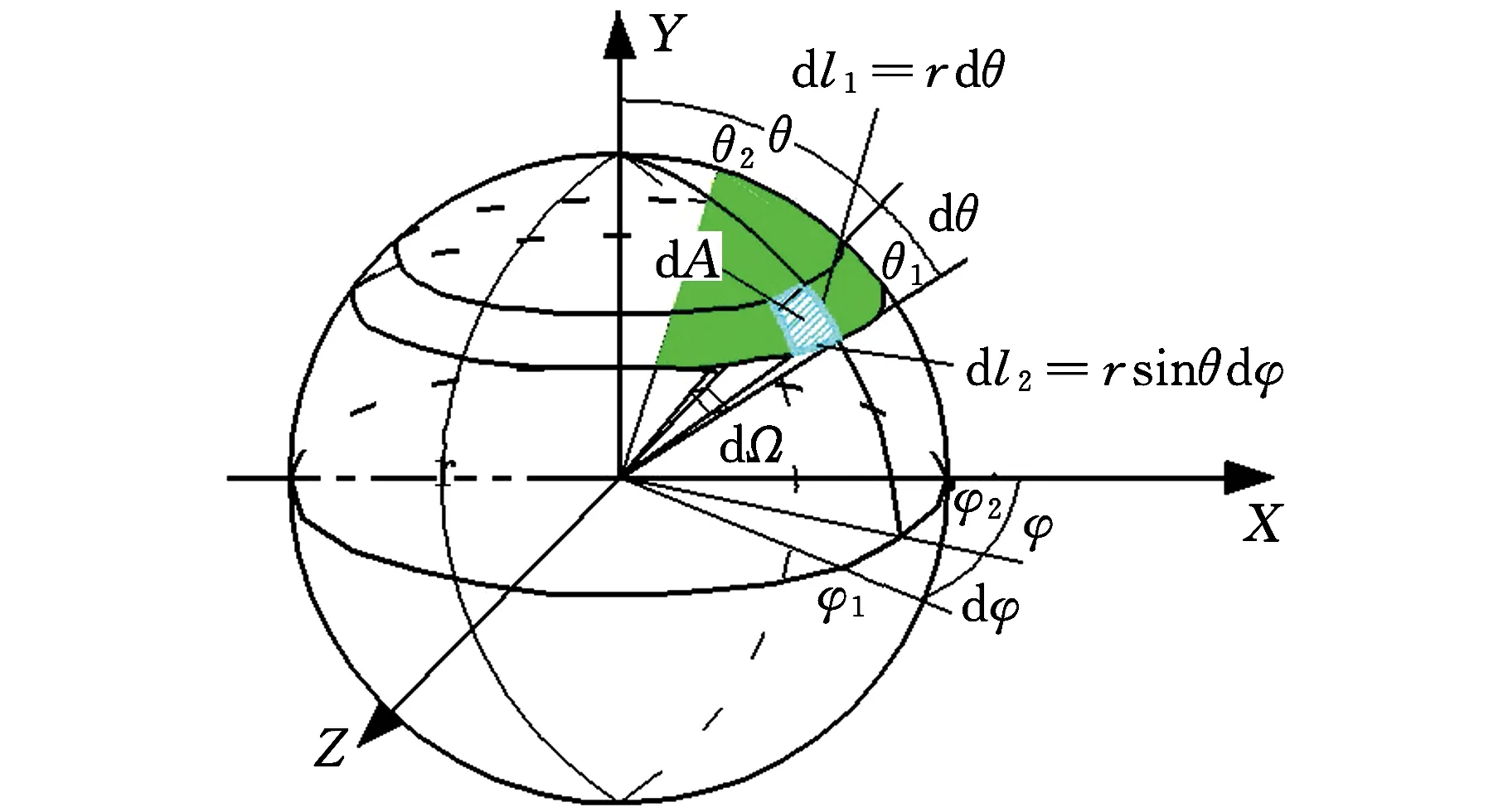
图3 向位妨碍的示意图Fig.3 A diagram showing the hindrance

同时，根据定义2可得具体妨碍值计算公式:

(1)

式中，θ1、θ2为拆卸射线在OXZ面与Y轴正方向由妨碍起点转到妨碍终点的妨碍夹角，通过投影可得到θ积分域为[0,π]；φ1、φ2为从正Y轴方向看自X轴按逆时针方向由妨碍起点转到妨碍终点的妨碍夹角，通过投影可得到φ积分域为[0,2π]。

为了明确表达两零部件之间的向位妨碍关系，假设单位球体被分成两个部分：一部分代表零部件j对零部件i产生的向位妨碍区间Rij，用灰色表示(图4球体左下部)；另一部分表示零部件i对零部件j产生的向位妨碍区间Rji，用白色表示(图4球体右上部)。根据上述定义可知，在非全向位妨碍和非无向位妨碍时，零部件i对零部件j产生的向位妨碍区间(r=1)为

Rji=4π-Rij

(2)

图4 三维空间约束向位妨碍示意图Fig.4 3D-space constraint hindrance diagram

若零部件j对零部件i产生的向位妨碍值为全向位妨碍，则用全灰色球体表示(图5a)；若为无向位妨碍，则用全白色高斯球表示(图5b)；若零部件i移动方向只有一个方向，则用白色锥体或箭头表示(图5c)，其他情况为部分向位妨碍，球面区域大小由妨碍区间大小决定(图5d)。

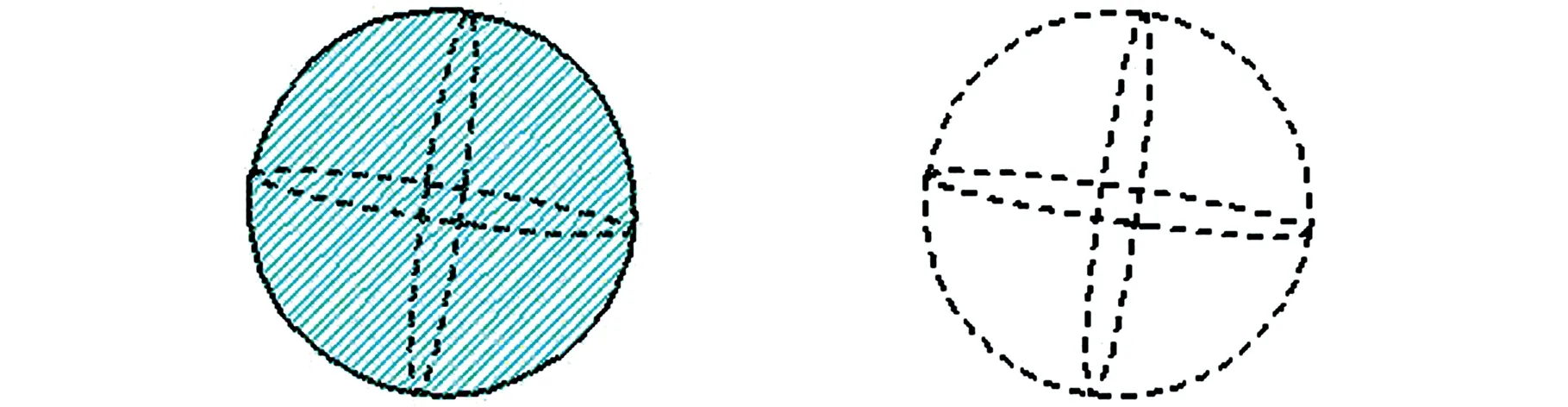
(a)全向位妨碍 (b)无向位妨碍

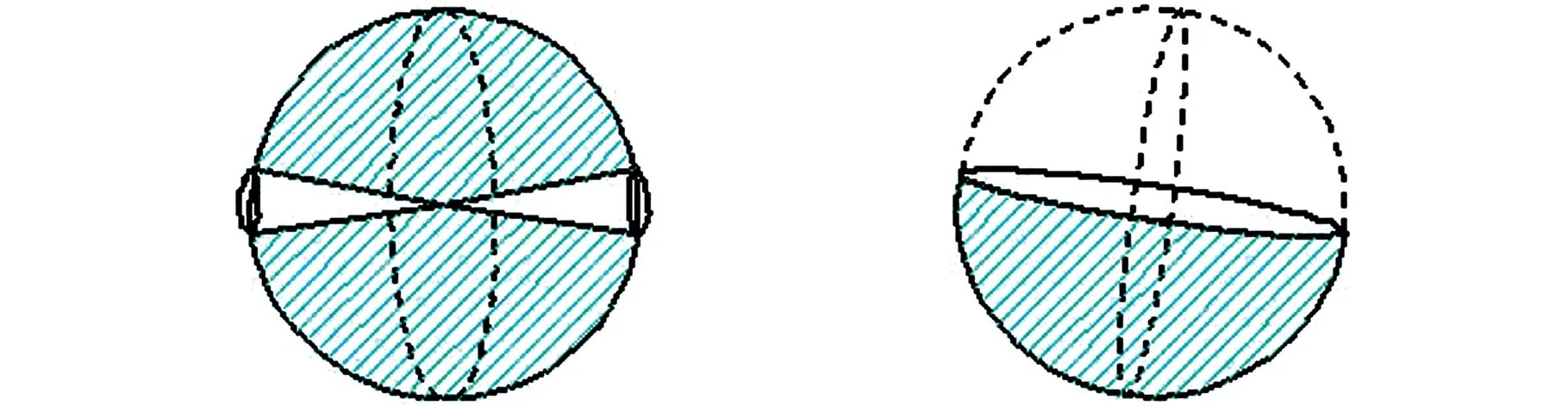
(c)轴类柱面接触妨碍 (d)部分向位妨碍图5 三维向位妨碍分类简图Fig.5 3D phase hinder classification diagram

1.2 三维向位妨碍区间分类计算

实际零部件之间的接触方式可以分为平面接触、曲面接触及其他接触。形锁合接触(链、带、齿轮)、材锁合接触(焊接、粘接)及无接触配合等都属于其他接触。

1.2.1平面接触

机械零件平面接触分为单面接触和多面接触，设零件A和零件B为平面接触，则根据向位妨碍定义可得出B对A的向位妨碍为RAB，如图6所示。根据式(1)得图6中平面接触向位妨碍值如下：

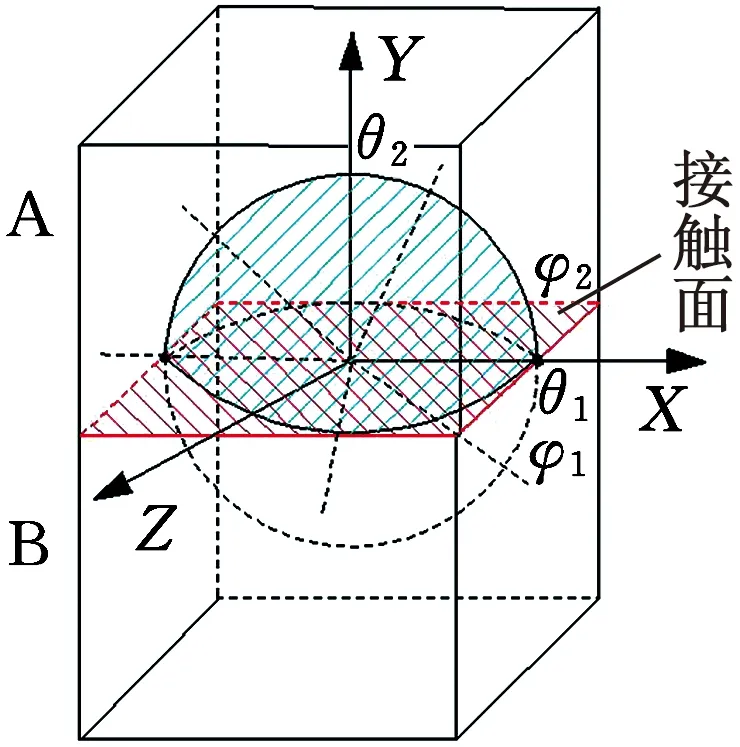
(a)单面接触

(b)双面接触

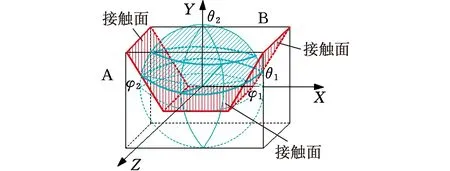
(c)多面接触图6 平面接触Fig.6 Plane contact

1.2.2曲面配合

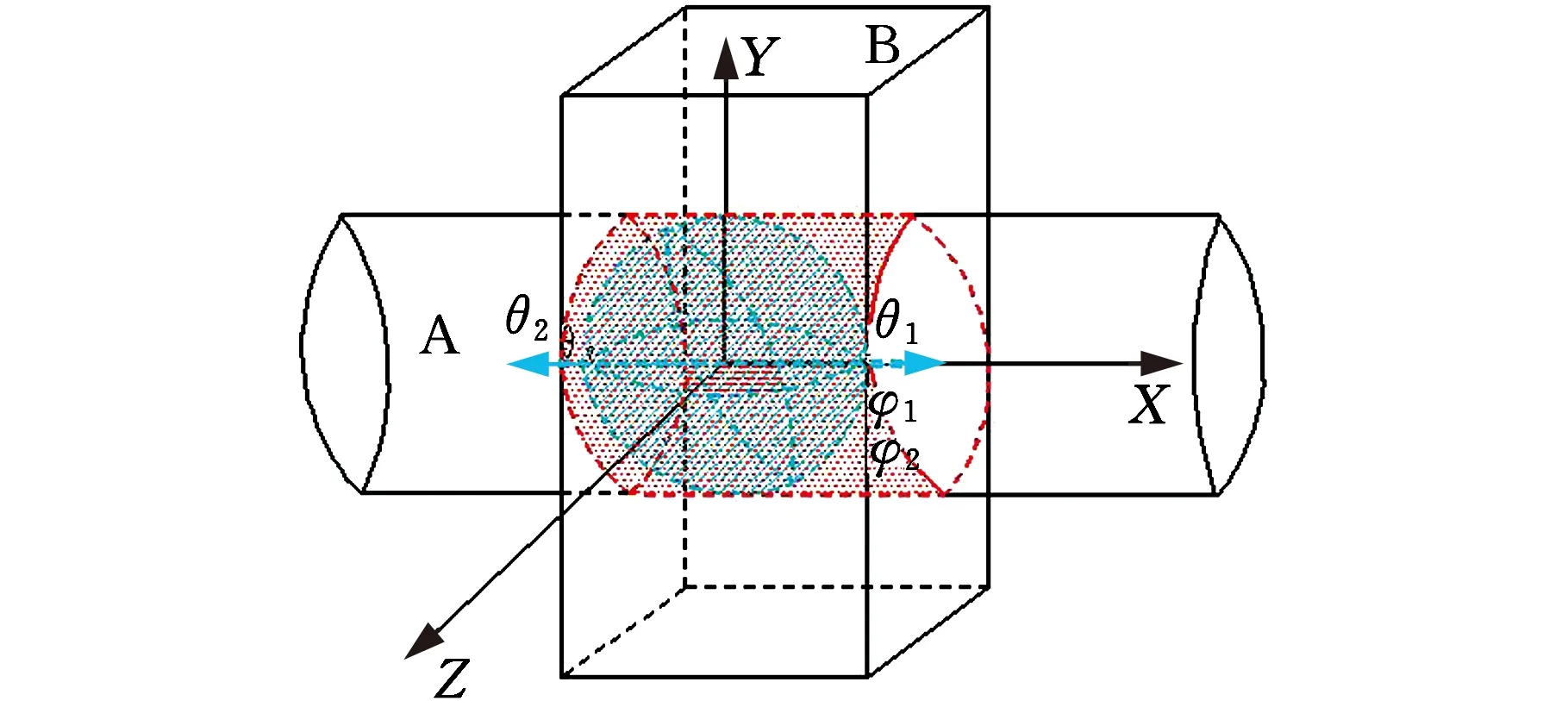
(a)螺纹配合

(b)过渡、过盈、间隙为H的孔轴配合

(c)圆锥类配合

(d)球面配合图7 曲面配合Fig.7 Surface combined

根据机械零件的实际特征和装配情况，曲面配合可以分为三类：第一类为柱面接触，可进一步分为螺纹配合和过渡、过盈、间隙配合；第二类为圆锥类配合；第三类为球面配合。设零件A和零件B为曲面接触，则根据向位妨碍定义可得出B对A的向位妨碍值RAB，如图7所示。根据式(1)得图7中曲面向位妨碍值如下：

(3)

(4)

其中，θ、φ可由图中或模型中求得,为过渡、间隙配合时，取“-”，为过盈配合时，取“+”，进而可以求出B对A的妨碍值。

(3)图7c为圆锥面接触配合，设锥角为α，图7c所示向位妨碍值

(5)

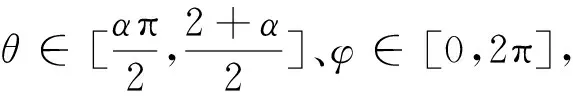
(4)图7d为球面接触配合，图7d所示向位妨碍值

(6)

其中，θ、φ可由图7d中或模型中的包裹角求得，进而可以求出B对A的妨碍值。

1.2.3形锁合接触

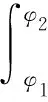
(7)

式中，α为啮合夹角；rB为齿轮B的分度圆半径。

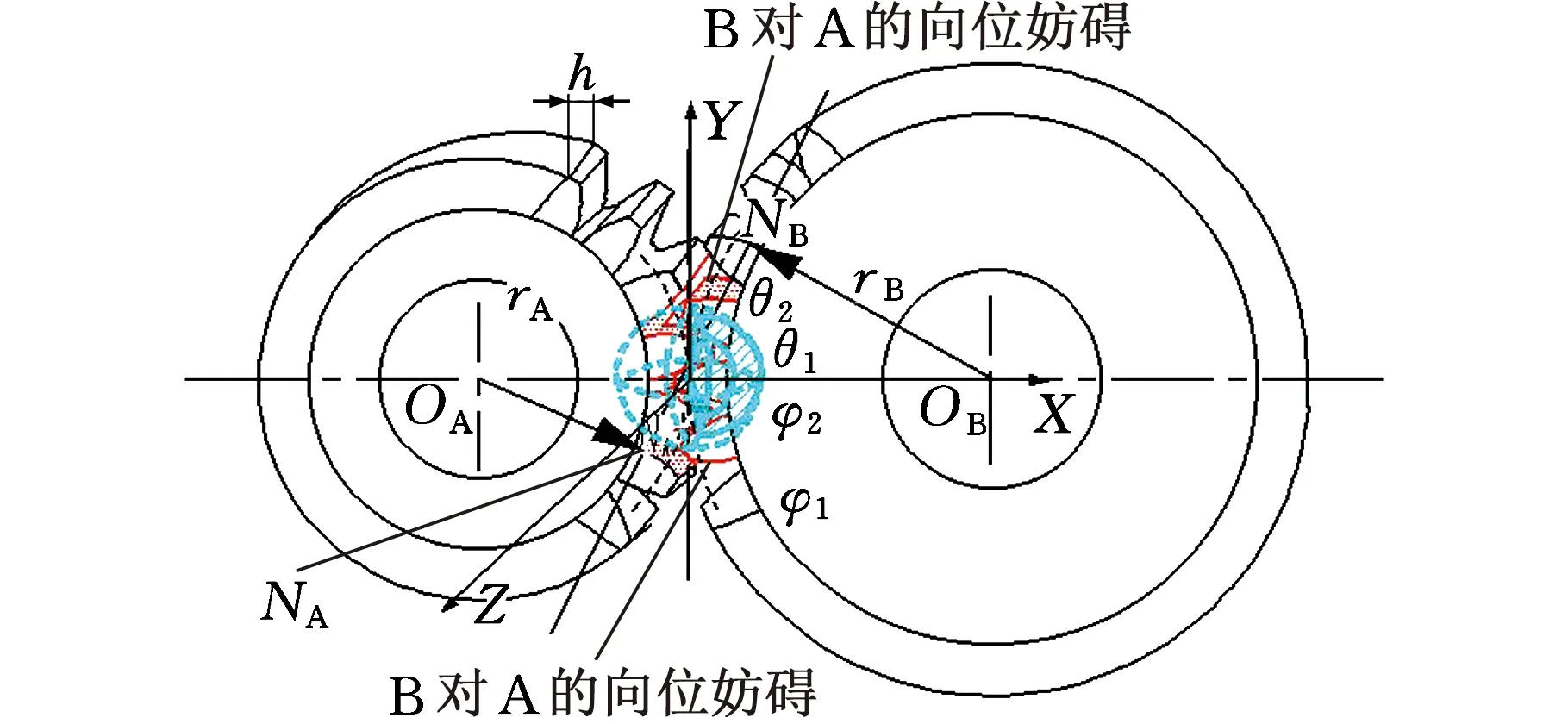
(a)齿轮啮合截图

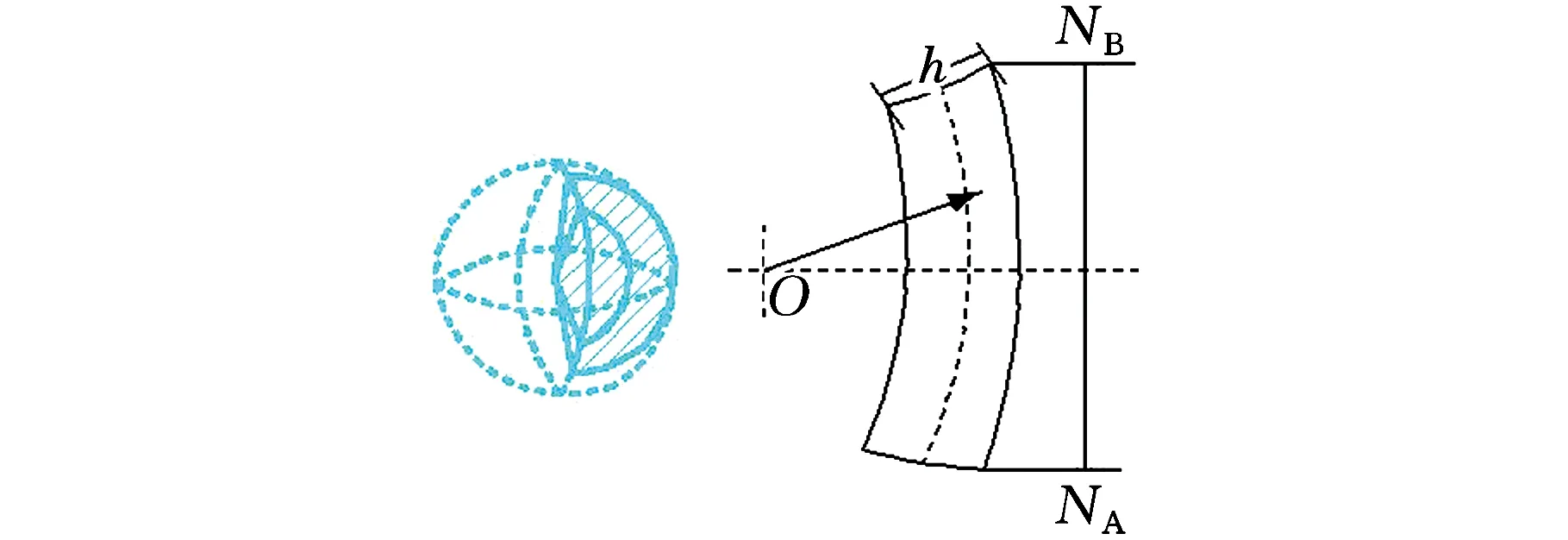
(b)齿轮啮合妨碍面图图8 齿轮啮合接触配合Fig.8 Gear mesh contact combined

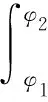
(a)普通V带与V带轮

(b)单根带实际的妨碍面积图9 带与带轮向位妨碍Fig.9 Belt and pulley hinder

(8)

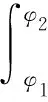
(9)

(a)链与链轮的接触

(b) 实际妨碍面积图10 链与链轮妨碍Fig.10 Chain and sprocket hinder

1.2.4材料锁合接触

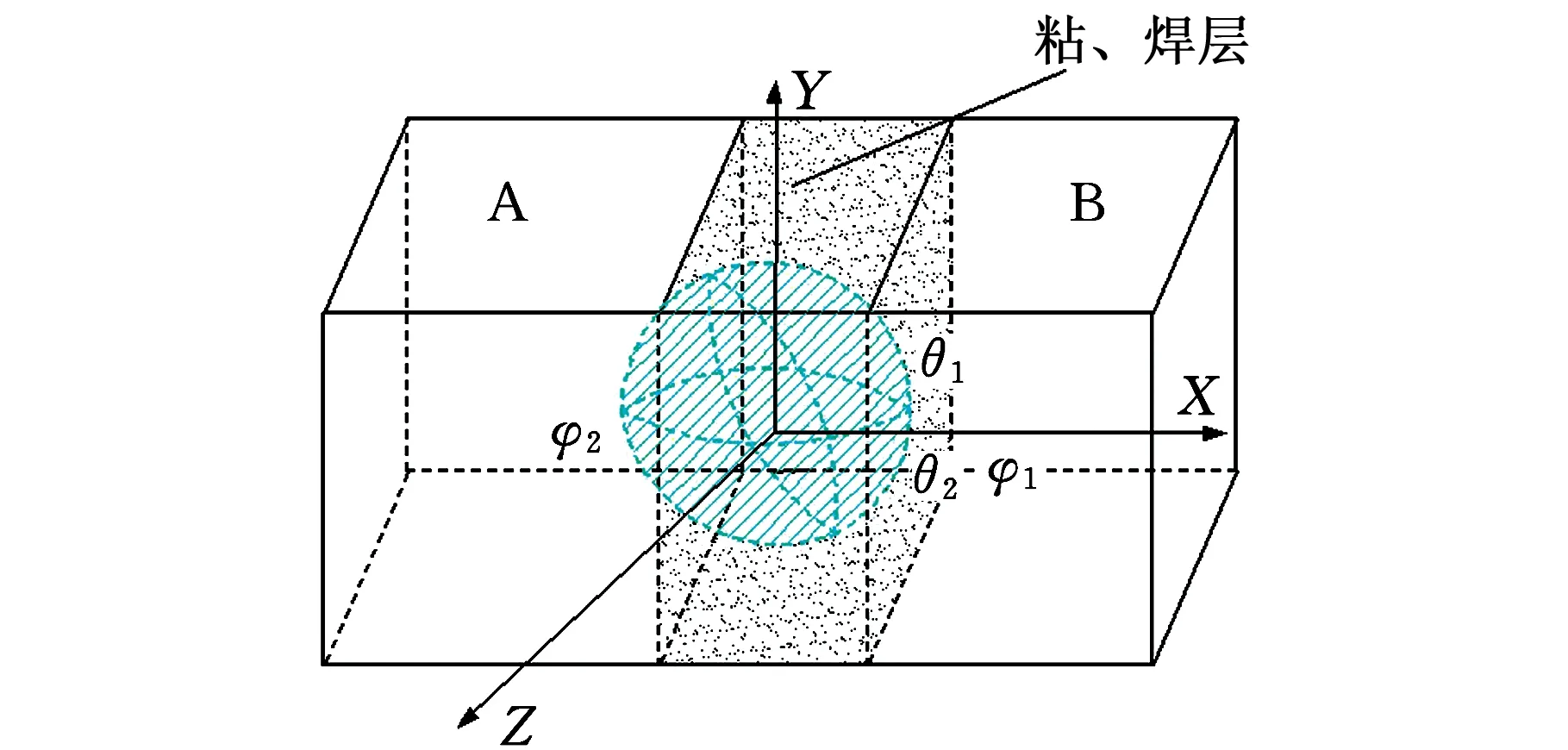
图11 材料锁合接触Fig.11 Material closure contact

材料锁合为材料内部结构组织粘合，如零件A和零件B粘合。图11为材料锁合接触，实际情况为材料内部结构组织粘合配合。没有移动方向，分析认定为全向位妨碍，有

(10)

1.2.5无接触配合

无接触配合为无结构组织结合或无接触的配合，零件A和零件B直接存在一定的距离，见图12。零件A和B可以自由移动，则认定为无向位妨碍，无向位妨碍值

RAB=RBA=0

(11)

图12 无接触配合Fig.12 No-contact combined

根据上述提到的机械零件之间的具体配合分类以及对应的三维向位妨碍计算方法，整理可得表1。

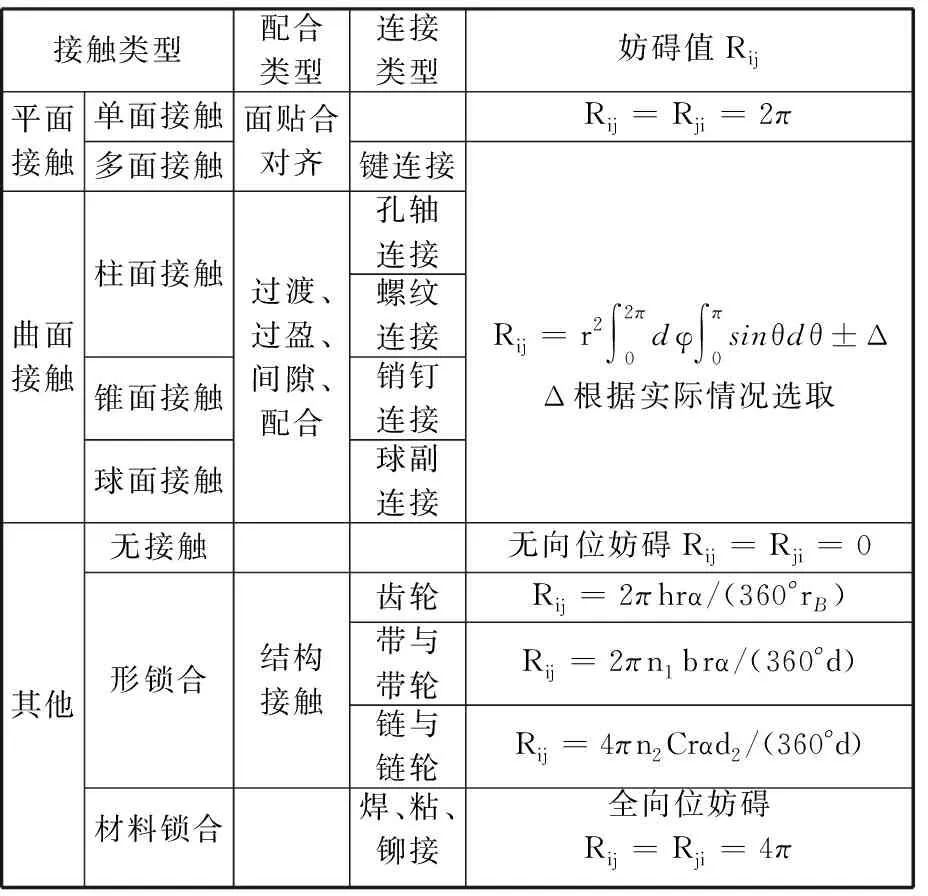
表1 机械零件装配分类及向位妨碍

1.3 基于向位妨碍的约束状态图

在废旧产品拆卸过程中，零部件的约束关系主要分为接触关系和连接关系。接触关系是指两零件之间的装配面配合关系，如平面接触、曲面接触等；连接关系是指零部件间的紧固连接关系，如螺纹连接、键连接、过盈配合、粘、焊接等。基于向位妨碍的约束状态图的具体定义如下。

定义3 设V为零件A的一个顶点集合，V的元素个数为|V|，当|V|>1时，任取V中的元素v1,v2,…,vn(n>1)，如果v1,v2,…,vn互不相交，那么定义edk={vi,vj}(k∈N;i,j=1,2,…,n;i≠j;n>1)为有向边，表示需要通过外力作用才能解除的连接关系。有向边用实线箭头表示，箭头元素的拆卸优先级小于箭尾元素的拆卸优先级，具有相同拆卸优先级的有向边其约束程度大小用向位妨碍区间大小Rij表示。

定义4 设基于向位妨碍的分类约束图集合GA={V,Ed(Rij)}，其中，Ed为有向边集合。定义产品在拆卸过程是一个从t0时刻一直到tn时刻的状态变化过程，记为GA(t)={V(t),Ed(Rij)(t)}(t=t0,t1,…,tn)。拆卸之前的状态集合GA(t0)={V(t0),Ed(Rij)(t0)}，第一个关联关系解除之后的状态集合GA(t1)={V(t1),Ed(Rij)(t1)}，依此类推，完全拆卸之后的状态集合GA(tn)={(V(tn),Ed(Rij)(tn)}。

将符合以上定义的集合约束图称为基于向位妨碍的约束状态图模型。图13为挤压机构装配示意简图，根据其零部件装配关系及向位妨碍关系可构建其t0时刻基于向位妨碍的约束状态图，见图14。

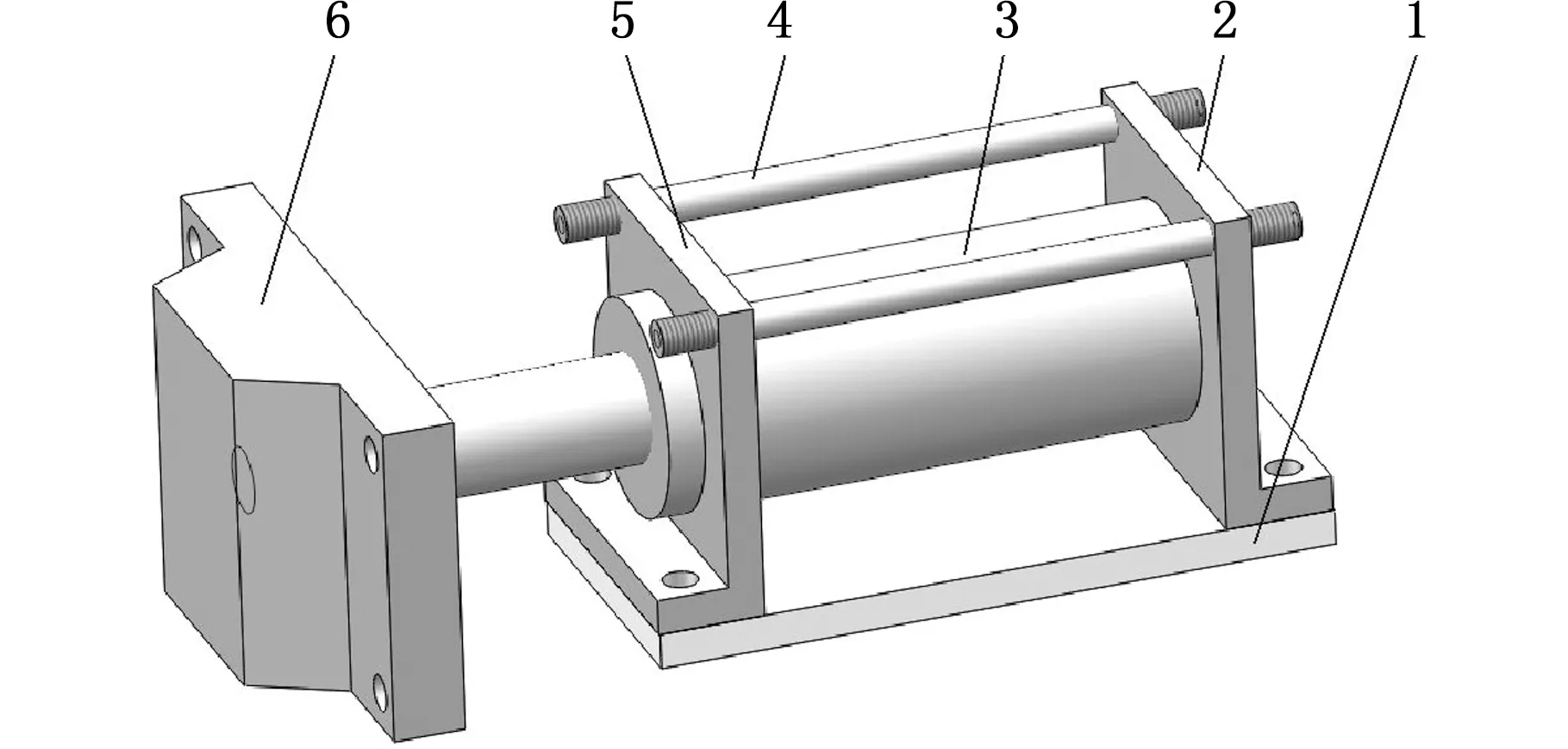
1.底座 2.前固板 3.液压缸 4.紧固螺柱 5.后挡板 6.挤压头图13 挤压机构装配示意简图Fig.13 Assembly schematic diagram of extrusion mechanism

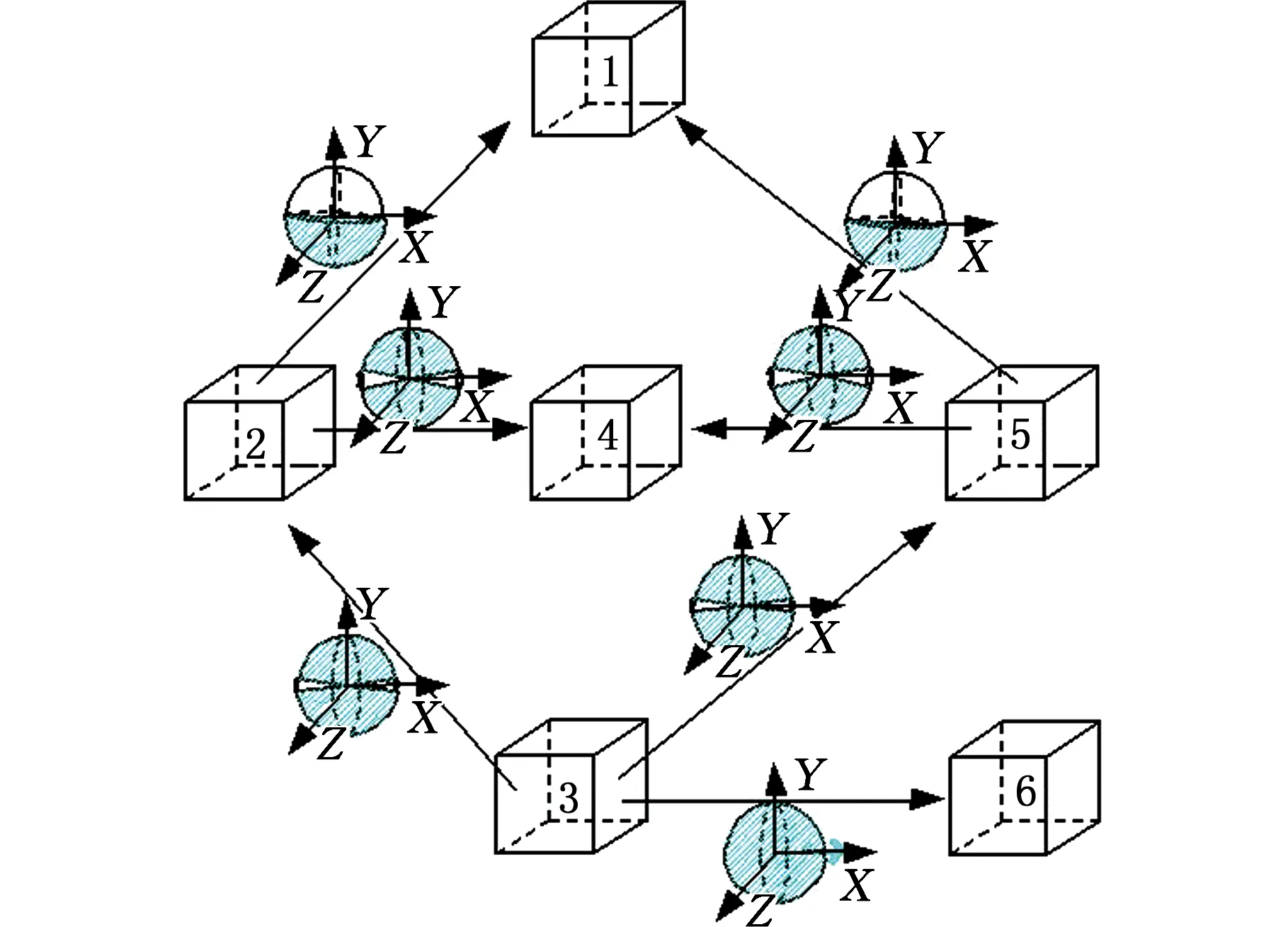
图14 挤压机构t0时刻基于向位妨碍的约束状态图Fig.14 Constraint state graph based on phase hinder of extrusion mechanism at t0

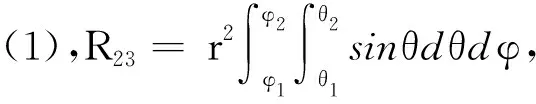
2 基于向位妨碍的约束状态矩阵

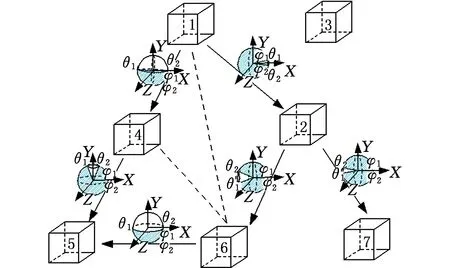
基于向位妨碍的分类约束状态矩阵M(t)(0

i,j=1，2，…，N

以图14为例，分析t0时刻基于向位妨碍的分类约束状态图，图中共有有向边7条。t0时刻的状态矩阵如下：

3 拆卸规则算子与拆卸路径生成

3.1 拆卸规则算子D

在构建了基于向位妨碍的分类约束状态矩阵M(t0)之后，产品的拆卸就是依据状态矩阵进行运算的过程。为了对状态矩阵进行有效的运算、搜索，需要根据状态矩阵构成特点制定优先拆卸的规则。具体内容如下：

(1)由于状态矩阵的行元素代表待拆卸零部件，列元素是对行元素有可能产生约束和妨碍的零部件，所以首先需要判定哪个行元素是无约束或被约束最少，并优先拆卸该零部件。

(2)如果有多个行元素的约束数量相同，则需要进一步判定向位妨碍区间值，向位妨碍区间值小的零部件优先拆卸。在不考虑其他影响因子的前提下,对于图6a，RABa=RBAa，那么拆卸A与B的难度相同；对于图6b，RABbRABb，那么对拆卸零件A来说图6a情况要难于图6b，反之对拆卸零件B来说图6b难于图6a。

(3)为了提高拆卸效率，对于行元素中存在相同约束数量，但向位妨碍区间长度不一样的情况，可实现多目标同时拆卸。

产品拆卸过程就是状态矩阵不断变化迭代的过程，每拆卸一项，相当于一个时刻t的变化。根据状态矩阵运算、搜索规则，构建了一个对状态矩阵操作的拆卸规则算子D。

定义5 假设待拆卸产品从初始状态一直到最终拆卸完成有n个状态，可表示为M(t0)、M(t1)、…、M(tn)，其中总存在一个矩阵DN×N使得M(ti+1)=DM(ti)(0≤i

3.2 拆卸路径生成流程

结合制定的拆卸规则，将拆卸规则算子D与状态矩阵M不断进行运算迭代可得到所有最优拆卸方案。拆卸序列规划流程如下(图15)：

图15 拆卸序列规划流程图Fig.15 Demolition sequence planning flow chart

(1)计算机读入状态矩阵M及元素全为1的算子矩阵D；

(2)搜索状态矩阵各行，寻找约束项最少的一行(约束个数要大于0，如果约束个数为0，则表示该零部件已拆卸)，假设为第m行；

(3)判断约束最少的行是否为单行,如果不是单行，则转到步骤(8)；

(4)如果是单行，则将D相应的第m列置为0；

(5)记录该行号，并计算M(tn+1)=DM(tn)；

(6)判断矩阵M元素是否全为0，如果是则输出拆卸序列方案，结束；

(7)如果不是则转到步骤(2)；

(8)如果是单目标拆卸，计算各行元素向位妨碍区间长度,并选择向位妨碍区间最短的行，假设为第m行,转到步骤(4)；

(9)如果是多目标拆卸，则把算子矩阵相应列元素置为0,同时转到步骤(5)。

4 实例分析

平口钳是一种通用可调夹具，适用于多品种小批量生产加工，也可用于组合夹具作为一种“合件”。由于其定位精度较高、夹紧迅速、通用性好、操作方便，因此应用广泛[21]。平口钳是易损易耗产品，对平口钳进行拆卸回收具有重要意义。图16为平口钳装配示意简图，根据其零部件装配关系及向位妨碍关系可构建其t0时刻基于向位妨碍的分类约束状态图，见图17。

1.螺杆 2.固定钳身 3.钳口板 4.活动钳身 5.紧固螺钉 6.螺母 7.固定圆环图16 平口钳装配示意简图Fig.16 Assembly diagram of flat nose pliers

图17 t0时刻基于向位妨碍的分类约束状态图Fig.17 Constraint state graph based on phase hinder at t0

依据所提出的拆卸算法与流程，具体实施如下：

(1) 从状态矩阵M(t0)中选取所在行元素为1和向位妨碍个数最少的项，结果为零件3和零件7。接着比较零件3和零件7所在行的所有妨碍区间集合长度，可得R3=2π，R7=2.66π，R3

此时t1时刻的状态矩阵

t1时刻的向位妨碍分类约束状态图见图18。

图18 t1时刻基于向位妨碍的分类的约束状态图Fig.18 Constraint state graph based on phase hinder at t1

(2)继续从状态矩阵中选取所在行约束的数量最少的项，约束个数为0，表示已经拆卸，这时选择零件7进行拆卸。继续将矩阵D第7列置为0，再与t1时刻状态矩阵进行计算，即

此时t2时刻的状态矩阵

依此类推，不断对状态矩阵和拆卸算子矩阵进行运算，在有多个约束数量相同的情况下，进一步计算向位妨碍的长度，依次对产品零部件进行拆卸。最终拆卸完成的标志是M(t7)、D7都为全零矩阵。此时可得到拆卸序列为：3-7-5-4-6-2-1。另外，如果在拆卸过程中需要进行多目标拆卸，这时候只需设定一个向位妨碍比较阈值，满足要求的零部件即可同时拆卸。

5 结论

(1)针对拆卸约束的描述与量化问题，提出了一种三维向位妨碍的概念与计算方法，并在此基础上构建了一种基于三维向位妨碍的约束状态图模型，以便拆卸决策中更合理、有效地对拆卸约束进行形式化、模型化和定量化描述与计算。

(2)在向位妨碍约束图模型基础上，构建了相应的状态矩阵和拆卸算子，一方面可分步描述产品的拆卸状态，另一方面将拆卸行为描述为拆卸算子与状态矩阵的迭代运算过程。

(3)在状态矩阵、拆卸算子、拆卸规则构建基础上，给出了一种产品拆卸序列自动迭代的运算方法，对于产品零部件复杂情况可借助计算机辅助实现产品拆卸序列规划。