面向再制造的拆卸线平衡问题建模理论及求解方法综述

张则强 蔡 宁 曾艳清 李六柯 邹宾森

西南交通大学机械工程学院，成都，610031

0 引言

废旧机电产品具有环境危害性和资源再生性双重属性，其回收再利用是实现可持续发展的重要出路之一，拆卸作为实现产品资源回收再制造的关键步骤，是组成产品闭环生命周期的重要环节[1]。传统方式对废旧机电产品的拆卸主要是依靠单人单台人工拆解，难以实现规模化拆卸和提高再制造效率，而拆卸生产线作为一种大规模生产的组织形式，具有生产效率高、成本低、易实现规模化、自动化生产等优点。为推动再制造的产业化，建造高柔性、敏捷性的拆卸线是实现批量拆卸的重要保障。然而，由于拆卸作业的复杂性、不确定性等因素，实际拆卸线的各工位间普遍存在着作业不均衡现象，影响生产效率的提升，再加之拆卸产品存在质量和数量的不确定性、失效模式的差异性，极大增加了拆卸线规划设计的难度,因此，合理规划拆卸方案、标准化作业流程，是提升再制造拆卸线平衡及作业效率的关键。

拆卸线平衡问题(disassembly line balancing problem, DLBP)一直受到学术界和工业界的广泛重视，学者采用了不同的方法对其进行求解，并扩展了多种与DLBP相关的模型。本文概述了DLBP及其基本数学模型,梳理了DLBP的求解方法并细分为三大类,总结了DLBP的扩展模型问题,最后对DLBP未来的研究内容和方向提出合理建议。

1 DLBP描述及模型

1.1 问题描述

DLBP是指：有一拆卸任务集合，每个作业任务之间存在优先约束关系，在满足节拍和优先关系等约束的前提下，确定拆卸工序顺序并将任务分配给各工位，使得工位数、各工位空闲作业时间尽可能少，拆卸效率尽可能高，最后将有用零件或部件回收。在DLBP中，表或图可用于优先关系约束和可行拆卸路线的直观表示，目前文献中主要存在两种关于DLBP的描述：零件优先关系图和任务优先关系图[2-3]。

零件优先关系图(part-based precedence diagram, PPD)表示依据优先关系的零件排序，每个任务导致一个零件被移除，该任务编号对应于移除零件的编号。产品拆卸可通过有向图G={V,E,U}来描述，其中节点集V表示拆卸任务集，弧集E表示优先关系集，有向图G的边数e=|E|；采用邻接矩阵IP=[ali]n×n表示拆卸任务的优先关系，其中ali为0-1变量，若任务l是任务i的紧前任务，则ali=1，否则ali=0；关联矩阵U表示拆卸任务关联信息集，存储任务时间、成本等。

任务优先关系图(task-based precedence diagram，TPD)依据其紧前任务提供优先关系约束，一个任务可能会导致一个或多个零件、组件的拆除，拆卸任务的编号不依赖于零件的编号，与PPD的对比见表1。AND/OR关系图(AND/OR graph, AOG)是一种基于任务的表达方式，可描述产品完全拆卸的所有路径，但由于AOG不能直接给出拆卸任务之间的优先关系，因此，KOC等[3]在AOG的基础上提出AND/OR关系转换图(TAOG)的描述方式，TAOG图中节点代表组件或者零件，超弧线代表一个拆卸任务，并连接经过拆卸后形成的两个组件或零件。

表1 PPD和TPD的对比

1.2 目标函数

在优化目标方面，工作站的数量最小化是最优选的目标，最常见的优化目标归纳如下[4]：①最小化工作站数目；②最小化均衡空闲时间；③最小化危害指数；④最小化需求指数；⑤最小化拆卸方向改变次数。上述5个目标分别表示为(部分研究文献中式(2)没有平方项)

f1=W

(1)

(2)

(3)

(4)

(5)

式中，W为开启工作站数目；n为拆卸产品拆卸任务数目；CT为工作节拍，是固定值；STk为第k个工位的所有拆卸任务时间之和；pi为任务i在拆卸序列上的位置；hi为0-1变量，若第i个拆卸任务有危害属性，则hi=1，否则hi=0；di为已知量，表示第i个拆卸任务的需求量；ri为第i个拆卸任务的操作方向，共分为±x、±y、±z6种；Ri为0-1变量，指拆卸序列上第i个位置上操作方向的变动性。

1.3 经典DLBP数学模型

为方便模型建立，经典DLBP常作如下假设：①拆卸产品的供货量是无限的；②拆卸产品为完全拆卸；③废旧产品零件无缺失、改造等情况；④废旧产品为单一品种拆卸且为直线形布局；⑤忽略零件或者组件在工作站之间的移动时间；⑥拆卸处于理想状态，忽略突发事件。

DLBP的数学模型描述如下[5-6]：

minF={f1,f2,f3,f4,f5}

(6)

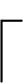
(7)

(8)

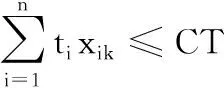
(9)

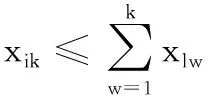
(10)

其中，xik为决策变量，若任务i被分配到工作站k，则xik=1，否则xik=0；ti为已知量，表示第i个拆卸任务的操作时间；式(7)为工作站约束，确立工作站数目的上下界限；式(8)为任务分配约束，保证每个拆卸任务必须被分配，且只能被分配到一个工作站；式(9)为节拍约束，保证工作站所有任务时间之和不超过规定节拍；式(10)为优先关系约束。除式(10)外，下式也可确立优先关系约束：

(11)

1.4 测试算例

由于DLBP的NP属性，求解难度较大，故研究者提出大量的求解方法。为了对这些方法的求解性能进行有效评价，现将文献中常见的拆卸求解实例进行汇总，以此作为DLBP的基准算例。

基于PPD的拆卸实例汇总见表2。

表2 基于PPD的拆卸实例

MCGOVERN等[16]首次提出19个不同规模的DLBP基准算例，验证蚁群算法求解DLBP的性能。具体构造规则满足7个要求：①拆卸任务数满足8≤n≤80，并且构成等差数列，任务数首项为8，公差为4，末项为80，总共19组拆卸实例；②不考虑拆卸任务之间的优先关系；③定义零件危害属性，若k=n，则对应零件hk=1，否则hk=0；④定义需求量，若k=3n/4，则对应零件dk=1，否则dk=0；⑤所有拆卸实例的节拍均为26 s；⑥定义拆卸方向

(12)

⑦拆卸任务时间分配满足

(13)

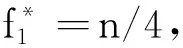
KOC等[3]提出基于TAOG的基准算例，其产生方式主要由3个参数来定义：a表示每个水平的虚拟节点B的数量，t表示每个虚拟节点B的任务(正常节点A)的数量，N表示零件的数量。每个水平参数a、t可以不同，参数t甚至可以在同个水平中不同。P(a,t,N)可表示任何一个随机算例，正常节点A的个数R(A)和虚拟节点B的个数R(B)的计算公式为

R(A)=a(N-2)+1

(14)

R(B)=a[t(N-3)+2]

(15)

基于TAOG的拆卸实例汇总见表3。

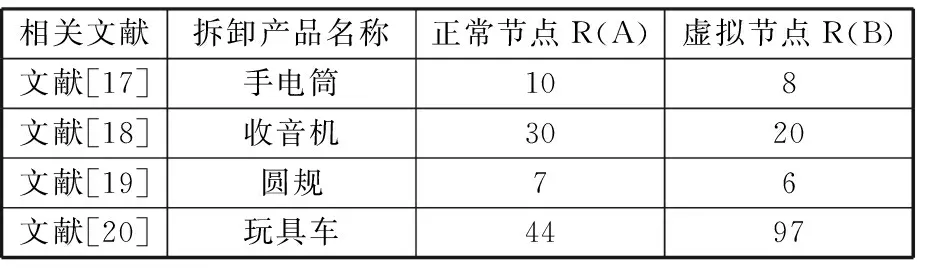
表3 基于TAOG的算例

2 DLBP的研究方法

设计高效的求解算法是DLBP的研究重点和热点之一，以所求结果是否精确，可以将求解方法分为精确方法和非精确方法两大类。精确方法主要包括整数规划、目标规划、动态规划等；非精确方法主要包括启发式方法[21]和元启发式方法。

精确方法在理论上是可以求解出DLBP问题的精确解的，但因受限于DLBP的NP属性，只能求解小规模问题，难以求解大规模问题。启发式方法和元启发式方法不能确定所求结果是否为精确解，但可以在合理时间内给出近似最优解，尤其在面对大规模多目标问题时，元启发式方法求解成为明智的选择。

2.1 精确方法

在精确求解方法中整数规划应用较多，研究重点是如何建立不同的整数规划模型，通过增加约束以减少搜索空间，运用成熟的数学规划软件(GAMS/CPLEX/LINGO/GOURBI)求解。为了处理任务时间不确定性，BENTAHA等[22]建立随机混合整数规划，采用L-shape和Monte Carlo相结合的方法求解最小线成本。表4对精确求解方法、优化目标及描述方式做了汇总和归纳。

表4 常见求解DLBP的精确方法

2.2 启发式算法

在拆卸线平衡方法中，启发式方法有贪婪算法、H-K算法或者几种启发式互相结合的方法等，主要思想是构造方法策略中的价值重要层次度。结合拆卸线本身的特点，通常使用位置权重法，在满足约束的基础上进行任务分配。

单一启发式方法求解DLBP受启发式规则影响大，且所求结果唯一，为了进一步提高求解质量，常采用多种启发式相结合的方法，分阶段优化。MCGOVERN等[31]提出贪婪算法和爬山搜索结合的两阶段优化策略的启发式方法，第一阶段在可行解的基础上，采用贪婪算法获得一个较优解，在考虑危害零件和需求零件的同时使工作站数目尽可能小，第二阶段采用爬山搜索进一步优化工作站数目或均衡空闲时间。AVIKAL等[21]采用Kano模型和改进理想点法(M-TOPSIS)，先通过多准则决策确定任务优先级，然后基于优先级大小和零件优先关系，将任务分配给每个工作站。在文献[21]两阶段优化的基础上，REN等[32]提出3阶段优化DLBP，第三阶段利用2-opt算法调整和改善优化结果。

虽然目前启发式方法已不是DLBP研究的重点，但启发式方法可为元启发式方法求解DLBP提供较好的初始种群，加快收敛速度，另外，可依据启发式规则进行快速解码，得到综合较优的工位分配方案。

2.3 元启发式方法

智能算法是DLBP求解方法的研究热点，它可在较短时间内求解出大规模DLBP的满意解或较优解。智能算法主要包含3个模块：编码、搜索策略、解码。在编码阶段主要采用基于任务的单层编码方式，这种编码方式直接产生一个个体X1×n=(1,2,…,n)，元素的个数等于拆卸任务数，个体中的每个元素对应于拆卸任务，依次拆卸则得到一种拆卸方案，如个体(1,3,2,6,5,8,7,4)表示拆卸序列为：1-3-2-6-5-8-7-4。此外，在编码阶段采用随机键编码[33]，随机产生和序列相同个数的随机数，在满足优先关系的基础上，对应随机数大的任务则优先拆卸。解码过程是将可行解序列分配到具体工作站，具体步骤如下：

(1)输入可行拆卸序列X、节拍CT，开启第一个工作站WS=1，当前工位剩余可分配时间为TR，令TR=CT。

(2)按照序列X的任务顺序，判断任务i的操作时间ti是否大于TR，若是，令TR=CT，并开启新的工作站，WS←WS+1，否则令TR←TR-ti。

(3)循环步骤(2)直至序列X的任务分配完毕，输出拆卸方案。

不同的算法搜索策略不一样，所以不同算法求解的效果不同。遗传算法、蚁群算法及人工蜂群算法在DLBP求解过程中运用的比较广泛。在遗传算法方面，文献[30]基于AOG的描述方法，构建作业时间随机的并行工位的DLBP的模型，考虑两种不同的适应度评估方法，并在交叉变异后的新解增加修复算法，采用多样化策略，取10%的Pareto非劣解和随机产生的方式更新种群；KALAYCI等[34]将遗传算法和变邻域搜索算法相结合来求解工序相依的DLBP模型(sequence-dependent DLBP, SDDLBP)，采用多种变异操作，产生不同的邻域结构，其效果优于其他多种算法；李六柯等[35]提出了一种Pareto免疫遗传算法，融合遗传算子和免疫算子，基于拆卸方向改变对作业时间的影响，建立考虑作业调整时间的DLBP模型，将算法与仿真技术结合进行求解。在蚁群算法方面，文献[16]研究蚁群算法(ACO)求解基本的DLBP问题，并通过19个规模的随机算例验证；丁力平等[5，12]将小生境技术嵌入更新操作中搜索Pareto最优解，算法使用Pareto思想来动态过滤获得的非支配解集。在人工蜂群算法方面，文献[36]采用启发式方法来产生初始解，引入危害和需求属性，依据任务的权重大小选择优先拆卸任务，采用可变步长的动态搜索策略，通过P25验证算法，然后运用于求解P52。文献[37]考虑在人工蜂群算法中融入变邻域算法思想，设计交换、插入、逆序和多次插入的多种邻域结构，针对多目标SDDLBP，采用字典排序方法处理多个目标，增加最小化总的拆卸时间目标，分别对P10、P25、P47求解进行算法验证和对比。文献[15]建立考虑能耗的拆卸线平衡问题的数学模型，并将能耗目标集成到成本和工作负荷的目标中，采用人工蜂群算法获得P32节能的拆卸方案。

随着元启发式方法的不断出现，有学者研究其他智能算法求解DLBP，如变邻域搜索算法[38]、人工鱼群算法[39]、猫群算法[40]、萤火虫算法[41]、教学优化算法[32]等。

3 DLBP的扩展和补充

建立合适的模型是DLBP的另一研究重点和热点。在基本DLBP模型的基础上，通过释放一些约束、假设条件，或添加一些符合实际的特殊因素，构成新的DLBP模型。目前扩展的模型有多种，依据不同的分类标准[42]归纳，结果见表5。

表5 DLBP扩展模型

基本DLBP是基于理想状况建立的优化模型，而实际拆卸过程具有高度不确定性和差异性，因此国内外学者开始研究复杂的实际拆卸过程。针对型号、系列不一致等或损坏程度不同，目前研究主要有以下几个方面：第一，工艺路线相近或属于同一类产品，可采用混流拆卸线；第二，可考虑作业时间的随机性，统计出拆卸作业时间的均值和方差，假设作业时间服从正态分布，允许在一定范围内随机波动，也可考虑作业时间是模糊的，通过三角模糊数确立拆卸作业时间；第三，建立不完全拆卸的模型或者部分拆卸模型，只拆卸有需求和危害的零部件，其余可采用暴力拆卸，考虑由于零部件损坏，导致紧后工序拆卸的零部件无法拆卸的情况，通过多阶段优化求解。

3.1 随机型DLBP

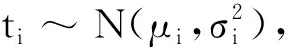
(16)

式中，μi、σi为第i个拆卸作业时间的均值和标准差；Sm为工作站m的任务集合；α为工作站满足节拍约束的概率；Φ-1(α)为概率α的反函数值。

针对废旧(EOL)产品，BENTAHA等[45-46]采用整数规划和Monte Carlo抽样、上下限二阶锥规划和分段线性近似精确求解。上述文献均考虑作业时间服从正态分布的情况，而现实拆卸过程中受干扰因素很多，拆卸作业时间可能不严格遵守正态分布，因此需要考虑其他更加符合实际的随机作业时间处理方法。

3.2 模糊型DLBP

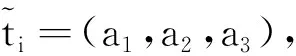
(17)

式中，a1、a2、a3分别为拆卸时间下界、最有可能时间、拆卸时间上界。

文献[10]针对自动引擎拆卸实例的模糊环境，考虑模糊作业时间及拆卸零件的模糊需求，采用模糊权重优化4个目标函数，分别通过GAMS和MATLAB软件求解，并使用模糊均值和分散排序技术比较所求结果优劣。除了考虑模糊节拍和作业时间，还可考虑模糊空闲时间和模糊平衡率[11]，上述文献均利用权重处理多目标，而文献[47]针对多目标模糊DLBP，采用融入Pareto思想的人工鱼群算法，并与文献[11]对比，表明所提算法更加有效。

3.3 考虑工序相依的DLBP

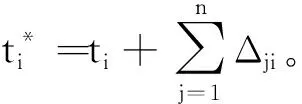
(18)

其他约束均不变。

KALAYCI等[34,38]对SDDLBP进行研究，以最小化工作站数目、均衡指数、危害指数和需求指数为优化目标，采用基于字典排序的多种智能算法对拆卸方案进行优化。与经典DLBP的主要区别在于改变了实际作业时间，所有任务的总拆卸时间是变化的，故将模型进一步扩展，增加最短总拆卸时间的目标[37]，以便减小工人和机器的作业负荷。SDDLBP与基本DLBP相比，改变了节拍约束的表达式，由于考虑干扰任务的时间增量，所以总的完工时间是变化的。进一步研究，可增加工具更换时间[15]和方向改变调整时间[35]，同时考虑不完全拆卸的情况，使模型进一步丰富。

3.4 U形布局DLBP

传统拆卸线都为直线形布局，待拆卸产品直线排列在传动设备上，工人分布在设备一侧。U形拆卸线是将设备按着“U”形排列，工人在设备两侧完成拆卸作业，U形布局与直线布局相比，可减少工人行走距离和工位数，提高拆卸效率，待拆卸产品入口和出口在同一侧，可降低物流成本，更加有利于平衡工作站时间。在基本模型的基础上，将任务分配约束、优先关系约束分别修改为

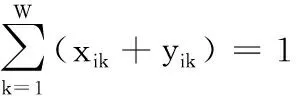
(19)

(20)

∀aij=1

式中，xik为0-1变量，若第i个任务分配在第k个工作站的入口侧，则为1，否则为0；yik为0-1变量，若第i个任务分配在第k个工作站的出口侧，则为1，否则为0。

文献[48]建立U形布局的拆卸线，提出一种启发式方法求解，最小化工作站的数量，同时处理有危害、高需求和低拆卸成本的组件或零件。在文献[44]基础上，谷新军等[49]建立多目标SMUDLB/S模型，通过基于分解和动态邻域搜索的混合多目标进化算法(HMOEA/D)求解，另外还考虑了需求零部件数量、危害属性及方向改变次数共10个影响因素，采用标准L12正交排列产生多个算例来验证。

3.5 平行拆卸DLBP

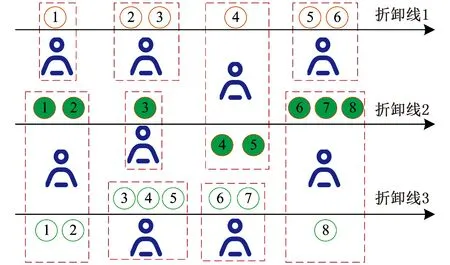
图1 平行布局拆卸线Fig.1 Parallel layout disassembly line

为了快速满足拆卸零件的需求，学者提出平行布局的拆卸线平衡问题，主要包括平行多线布局和并行工位布局，分别如图1和图2所示。平行多线布局拆卸线可以拆卸不同的产品，实现工位共享，有效减少工位数；同时装配线和拆卸线混合平行布局，可允许部分拆卸的有用零部件经过处理后，直接供货给装配线，减少备货时间及物料搬运路径。并行工位布局拆卸线虽然会导致额外成本的增加，但一方面可缩短节拍时间和提高拆卸效率，另一方面，提高生产线的柔性和可靠性，若并行工位发生故障，允许生产线以较低的生产率运行，不会造成停产。

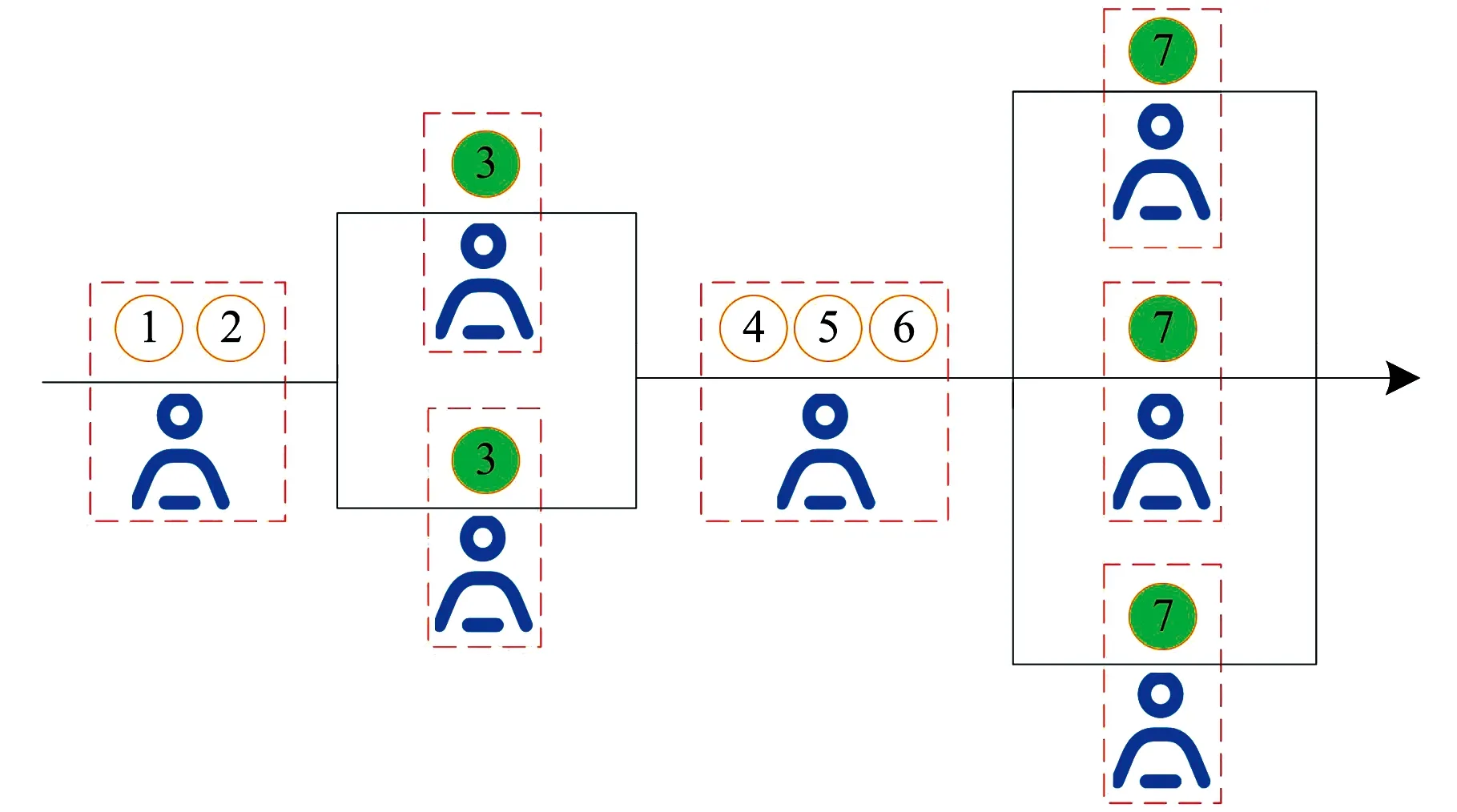
图2 并行工位拆卸线Fig.2 Parallel workstation disassembly line

HEZRE等[2]首先提出平行拆卸线平衡问题(parallel DLBP, PDLBP)，考虑拆卸过程中两条平行直线布局拆卸线，并和直线形布局DLBP对比，发现平行DLBP改善了工作站数目，为研究平行DLBP提供了研究基础，但仍存在很多地方需要进一步研究，如没有考虑平行DLBP特有的约束和假设，另外，文中采用的最短路径模型不能够在合理时间求解大规模问题。文献[20]将装配线和拆卸线混合布局，采用正逆向平行生产线，产线设置相同的节拍和速度，运用到汽车拆解上，通过蚁群算法得到较优的拆卸方案，提高汽车的拆卸效率。因此后续研究可采用启发式规则或元启发式方法求解大规模问题，考虑多条平行拆卸线或者多条线平行U形布局。

AYDEMIR-KARADAG等[30]首次提出并行工位拆卸线平衡问题，文中以拆卸线平滑指数和设计成本为目标，基于TAOG描述方式，采用改进遗传算法求解所提多目标DLBP模型。文中通过一个0-1决策变量限定工作中心的并行工位最多为2个，但在实际拆卸过程中，为更好地提高拆卸效率和可靠性，可能需要的并行工位多于2个，则无法通过简单的一个决策变量控制，为此需要进一步考虑并行工位DLBP其他特有的约束和假设，提高并行工位的数目上限，这进一步增加了模型的难度。

3.6 混合品种DLBP

目前，针对单类产品的拆卸平衡线研究较多，但为了及时响应市场需求，提供所需的零部件，需研究多产品柔性拆卸线。将产品单个回收并分类，考虑工艺近似的产品进行混合拆卸，如电视机类、冰箱类等，在混流拆卸过程中，目前主要求解思想是依据不同产品的优先关系得到综合优先关系图，进而获得综合作业时间表，然后当作一个理想化的混合产品来处理，混流DLBP求解难度比基本DLBP难，因为不仅要考虑拆卸序列和工位分配问题，还需要得到不同产品的具体排序过程。

文献[49]提出混合整数规划求解混流DLBP，基于TAOG表达考虑手电筒和收音机混流拆卸情况，首次利用二元模糊目标规划和模糊多目标规划方法求解混流DLBP。文献[44]不仅考虑混流拆卸，同时融入U形随机拆卸线平衡问题，基于PPD的表述方式，将不同产品的优先关系图汇总得到综合优先关系图，将模型进一步扩展。

3.7 不完全拆卸DLBP

在实际拆卸过程中，有些零部件已损坏或没必要完整拆卸，可采用暴力拆卸方式，因此，部分零件可以直接破碎，通过自动分拣机分离不同类型的可用颗粒，或者因回收的利润低于拆卸成本而不必进行拆卸作业，这大大减少了拆卸工作。由此,拆卸过程与装配过程不同，实际拆卸过程通常是部分拆卸[14,18,23,50-51]。在拆卸时，可能需要不同数量的零件和组件，这意味着不同的拆卸深度或速率，因而在基本模型中考虑利润的目标函数：

(21)

对任务分配的约束修改为

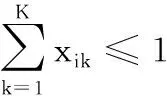
(22)

式中，ci为任务i的拆卸成本；zk表示0-1变量，若第k个工作站开启，则为1，否则为0；F为工作站开启固定成本;S为工作站单位时间运行成本;Ri为单位需求零件i的拆卸利润;xi为拆卸零件i获得的单位数量。

文献[18]基于AND/OR关系图，提出基于拆卸任务失败的DLBP模型，考虑由于零部件损坏，导致紧后工序拆卸的零部件无法拆卸的情况，分两阶段优化求解，第一阶段建立预测平衡，第二阶段给定拆卸失败的任务，然后重新分配任务。文献[50]针对供货有限及部件可用性的不完全拆卸，提出两个数学模型，第一个优化整个拆卸节拍的利润，第二个优化整个拆卸计划周期范围的利润，最后采用CPLEX精确求解。不完全拆卸DLBP主要思想是在满足拆卸需求的同时将危害零件全部拆卸，以最大经济利润和拆卸深度为主要优化目标，与基本DLBP相比，任务分配约束由式(8)改变为式(22)。

3.8 DLBP与供应链集成优化

针对供应链网络模型，将物流供应链与DLBP集成优化[24-25,52-53]，不仅考虑拆卸中心和工厂之间的组件或零件流，还需要考虑顾客到回收中心的废旧产品流，在整个物流网络中，同时优化DLBP和逆向供应链或闭环物流网络中涉及的顾客、回收中心、拆卸中心以及工厂，使拆卸工位和总物流成本最小，让整个物流网络高效运行。

4 结论与展望

DLBP具有重要的学术研究价值和应用价值，目前研究主要集中于算法和模型方面，提出了很多有效的求解算法，建立了多种数学模型，并开拓了DLBP的扩展问题和应用实例。纵观各方面的研究现状，DLBP的研究领域还存在下列问题值得进一步探讨和研究：

(1)在模型层面，虽然DLBP已扩充很多模型，但为了更加注重模型的实用性和扩展性，需重点研究不同布局形式和不确定条件下的多约束多目标问题。可从以下几个方面入手：①在实际拆卸过程中，会存在特定的约束，如考虑固定工位约束、相斥约束等新的约束条件；②目前优化的目标多涉及经济角度、平衡角度，可结合环境、资源等指标，扩充相关的目标函数来度量，从多个维度建立多目标优化模型；③考虑多线的不同连接方式，如垂直连接、平行连接和DLBP混合连接方式等，缩短货物供应和转运时间；④依据不同布局形式，可深入研究双边、平行拆卸线的情况；⑤目前大多数DLBP是基于节拍已知的情况，可拓展深入研究节拍未知的第二类DLBP问题；⑥考虑产品相关拆卸信息的高度分散性和不确定性，如使用年限、损坏程度等差异性，解决复杂实际拆卸问题。

(2)在方法层面，以往针对多目标优化问题多采用权重、字典排序等方法，近年来，多目标优化中引入Pareto思想，但得到的多个非劣解依然难以抉择，为此可采用先优化后决策的思想，引入多准则决策技术，筛选得到最满意的唯一解；另一方面，Pareto 支配会降低高维目标的排序效率，改进高维DLBP的非支配解排序方法显得格外重要，而NSGA-Ⅲ、HMOEA/D及模糊支配度具有求解高维多目标优化问题的优势，可将其运用到DLBP中。为求解大规模DLBP，高效元启发式算法将是一个重要研究方向，可研究新的编码和解码方式，例如多层编码或多段编码；另外还需探讨高效的搜索策略，寻求多种离散化操作设计。

(3)在应用层面，目前DLBP的研究大多局限于确定问题，相关应用的研究领域有限，有必要依据具体实际特征，进一步拓宽其对应的应用范围。一方面，不断将DLBP相关理论和算法研究发展和完善，注重涉及实际DLBP问题，运用到机电产品的拆卸回收或检修，例如汽车拆卸、轨道车辆检修等；另一方面，将解决DLBP的算法推广至求解其他离散优化问题中。