基于单服务器的群上幂指数安全外包计算方案
李 帅 付安民 苏 铓 陈珍珠 孙银霞
1(南京理工大学计算机科学与工程学院 南京 210094) 2(贵州大学贵州省公共大数据重点实验室 贵阳 550025) 3 (南京师范大学计算机科学与技术学院 南京 210023) (1373975356@qq.com)
云计算是一种新兴的计算模式,它将计算任务分布在大量计算机构成的资源池上,使各种应用系统能够根据需要获取计算力、存储空间和信息服务.随着云计算的快速发展,出现了一种新的计算模式:外包计算.外包计算允许使用资源受限设备(如智能手机和平板电脑)的用户将复杂计算任务外包给云服务器,从而节省计算时间.
但由于云服务器并不是完全可信的,因此也遇到一些新的安全问题和挑战[1-4]:1)用户数据经常会包含一些隐私信息(如个人医疗记录、个人收入状况和家庭成员信息等),而这些信息用户并不希望泄露给云服务器.因此,如何保护用户敏感的输入/输出信息是数据外包计算过程中的首要安全挑战.2)外包计算通常需要大量的计算资源,云服务器可能为了节省计算资源而“偷懒”,并且软件上的漏洞或者来自敌手的恶意攻击都可能会影响云服务器计算结果的正确性.因此,如何有效验证云服务器返回计算结果的正确性是数据外包计算过程中另一个安全挑战.
在密码学领域,将昂贵的计算外包给不完全可信的设备受到广泛研究[5-14].Chaum等人[5]首次提出了“wallets with observers”的概念,在每次执行任务时允许用户在自己的设备上安装一块硬件来执行计算.Hohenberger等人[6]进一步给出了外包计算的安全定义和安全模型,并基于不可信的双服务器模型,提出了首个幂指数运算安全外包方案.但可惜该方案对服务器返回的计算结果的可验证概率仅为1/2.陈晓峰等人[7]在Hohenberger方案的基础上,基于双服务器模型,提出了一个新的幂指数运算安全外包方案,其对服务器返回的计算结果的可验证概率提高到了2/3.最近,任艳丽等人[13]提出了一个新的基于双服务器模型的幂指数运算安全外包方案,其对服务器返回的计算结果的可验证概率达到了1.值得注意的是,文献[6-7,13]方案中都是基于不可信的双服务器模型,并且它们都要求双服务器之间不能进行共谋.Dijk等人[9]首次提出了基于单个不可信服务器的幂指数运算外包计算方案,但该方案在外包计算过程中服务器能够获取到指数运算中的底数,因此,该方案并不能有效实现数据的隐私保护.
在幂指数外包计算领域,特别是基于不可信的双服务器模型方面,学者提出了大量可验证计算外包方案,但现有方案大多关注的是数域上的幂指数运算外包,而鲜有关注群域上的幂指数运算.群域上的幂指数运算在基于身份签名[15-16]、盲签名[17]等领域有广泛运用.特别是现有的云存储可证明的数据持有[18-24](provable data possession, PDP)方案大都需要涉及到大量群上的幂指数运算操作.因此,最近Wang等人[8]提出了一个群上的幂指数运算安全外包方案,该方案基于单个不可信服务器,能够有效实现底数和指数的隐私保护,但可惜该方案对服务器返回的计算结果的可验证概率仅为1/2.
本文基于单服务器模型,提出了一个新的群域上的幂指数运算安全外包方案GEXP(outsourcing power exponent on a group field),能够有效避免双服务器模型存在的共谋攻击问题.GEXP通过使用一种新的数学分割方法,用户可以将原始数据安全分割成随机片的形式,从而很好地实现了数据外包中的隐私保护.同时,与已有方案相比,GEXP能够实现对外包计算结果的可完全验证.此外,针对云存储数据完整性保护方案中普遍涉及到大量群域上的幂指数运算问题,本文还给出了方案GEXP在一个典型的云端群组数据完整性验证方案Panda中的具体应用.
1 问题描述
1.1 系统模型
一个安全的外包算法包括2个不同的实体,如图1所示.首先,用户User调用子程序RandG产生盲化随机对;然后,User借助子程序产生的随机对实现了对原始数据的分割隐藏,将盲化后的随机数对上传到公共云服务器(public cloud server, PCS);PCS利用这些盲化随机数对进行计算,并将计算后结果返回给User;最终,User验证PCS返回的计算结果的正确性.外包算法中涉到的2个实体的描述如下:
1) 外包用户(User).有很多复杂的计算任务需要去处理,但缺乏足够的计算资源.
2) 公共云服务器(PCS).由公共云服务提供者进行管理.海量的存储空间和强大的计算能力为其处理用户的计算任务提供了强有力的保证.但是,通常情况下公共云服务器并不是完全可信的.
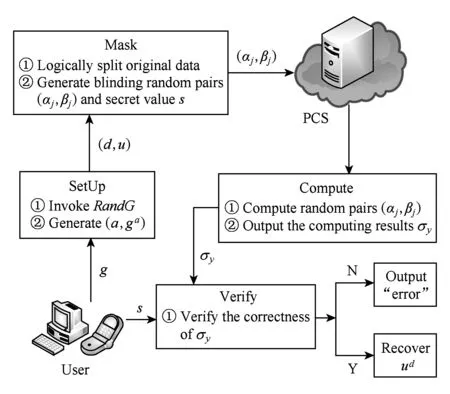
Fig. 1 System model图1 系统模型
1.2 安全定义
定义1. 安全的幂指数外包算法.该算法由4个子算法组成:
1) SetUp(g).使用变量g来初始化子程序RandG,用户调用RandG生成一些盲化随机数对(a,ga).
2) Mask((d,u),(a,ga)).输入原始数据(d,u)和盲化对(a,ga).使用逻辑分割算法将原始数据分割成随机片的形式.这些随机片由2部分组成:①需要PCS计算的盲化后的随机数对(αj,βj);②用来验证最终计算结果正确性的秘密值s.
3) Compute((αj,βj)).输入由Mask算法分割产生的随机数对(αj,βj),PCS输出相应的计算结果σy.
4) Verify(σy,s).输入PCS返回的计算结果σy和秘密值s来对结果进行验证.如果验证没有通过,用户输出“error”;否则,User恢复最终的计算结果ud.
2 幂指数运算的安全外包计算方案
本文提出了一个基于单个不可信服务器模型的群上幂指数运算的安全外包方案GEXP,在方案GEXP中,用户User借助子程序RandG实现了将指数运算安全外包给云服务器PCS,所提出的算法能够确保敌手A在整个外包计算的过程中不能获取到任何关于输入和输出的隐私信息.我们首先假设p是一个大素数,G是一个阶数为p的循环群.方案GEXP的输入为u∈G和d∈p,输出为ud.
2.1 子程序Rand
在幂指数外包方案中,普遍需要使用一个称为Rand的子程序来生成随机盲化对[6-8].Rand的输入是一个素数p和一个底数g∈(也有可能是其他的数值),每次调用后输出一个具有(a,gamodp)形式的随机的、独立的盲化对,其中a∈为了提高安全性,Rand的输出分布应该与真正随机的情形是计算上不可区分的.有2种方式可以用来实现这个子程序:1)检查表方法;2)预处理技术[10].
本文中我们使用了和文献[8]类似的扩展子程序RandG,其输入是一个p阶循环群G的生成元g,其中p是一个大素数,也有可能是一些其他的数值,每次调用的输出是一个具有(a,ga)形式的随机的、独立的盲化对,其中a∈
2.2 幂指数外包方案
我们提出的幂指数运算安全外包方案由4个子算法组成:
1) SetUp(g).用户User首先使用变量g来初始化子程序RandG,然后5次调用子程序RandG生成5组随机盲化对(α,gα),(β,gβ),(λ,gλ),(η,gη),(t,gt),并定义v1=gα,v2=gλ.
2) Mask((u,d),(a,ga)).子算法Mask是用来对原始数据u和d进行逻辑分割处理,将原始数据分割成随机片的形式.使得服务器PCS在计算过程中不能获取到任何输入输出的敏感信息.第1次逻辑分割:
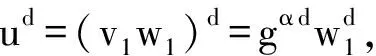
(1)
其中,w1=uv1.第2次逻辑分割:
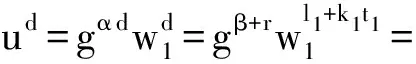
(2)
其中,β=αd-rmodp和l1=d-k1t1modp.下面对ud进行一组类似的逻辑分割:
(3)
其中,w2=uv2.
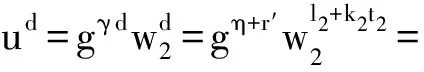
(4)
其中,η=λd-r′ modp和l2=d-k2t2modp.
通过上述的逻辑分割,底数u已经由随机数对(v1,w1)和(v2,w2)实现了隐藏,指数d则由随机值l1,k1,t1和l2,k2,t2来进行隐藏处理.
3) Compute((αj,βj)).用户User上传盲化后的数据对(rt,gt),(r′t,gt),(l1,w1),(l2,w2),(k1,w1),(k2,w2),云服务器PCS计算的指数运算并将相应的计算结果σy={gr,gr′,,,,}返回给用户User:

(5)
4) Verify((σy,s)).当收到云服务器PCS返回的计算结果σy后,用户User利用秘密值s(t1和t2)来验证云服务器PCS返回计算结果的正确性,即验证
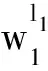
(6)

值得注意的是,为了进一步提高输入的安全性,逻辑分割中使用的随机盲化因子t1,t2通常至少选取64 b长度[8].
3 安全分析
本节我们从正确性和安全性2个方面来对设计的幂指数外包方案GEXP进行分析和证明.由于篇幅限制,本文没有给出完整的幂指数外包计算安全定义与模型,具体请参阅文献[6].
3.1 正确性
定理1. 基于单个不可信的服务器模型,算法(T,U)是方案GEXP的一个正确的实现,其中,输入(d,u)可能是诚实的、秘密的输入,或是诚实的、受保护的输入,或是恶意的、受保护的输入.
证明. 如果云服务器PCS是诚实的,用户User可以执行计算:

(7)
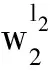
(8)

证毕.
3.2 安全性
定理2. 基于单个不可信的服务器模型,算法(T,U)是方案GEXP的一个安全外包实现,其中输入(d,u)可能是诚实的、秘密的输入,或是诚实的、受保护的输入,或是恶意的、受保护的输入.
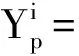
证明UVIEWreal~UVIEWideal.如果输入(d,u)不是诚实的秘密的输入、诚实的受保护的输入和恶意的受保护的输入情形时,U′总能获取到输入信息.显然,在这种情况下,模拟器S2的执行过程将与实际的实验中相同.因此,我们仅仅需要考虑输入是诚实地秘密的、诚实地受保护的和恶意地受保护的情形.在理想的实验环境中,模拟器S2的执行过程如下:当接收了第i轮的输入后,S2以(αj,βj)的形式向U′进行了6次随机询问;然后S2保存它自己的所有状态以及U′的状态.同上面证明EVIEWireal~EVIEWiideal的过程类似,在实际实验中U′的输入和理想实验中由S2随机选择的输入是计算上不可区分的.尽管E能够区分出实际实验和理想实验这2种不同的情形,但是E却不会将这些信息传递给U′.因此,我们可以得到UVIEWreal~UVIEWideal.综上所述,算法(T,U)是方案GEXP的一个安全外包实现.
证毕.
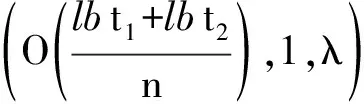
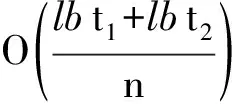
当外包用户User收到服务器PCS返回的计算结果后,User能够通过验证
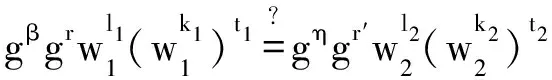
(9)
是否成立来判断服务器PCS是否产生了正确的响应.
如果等式不成立,表明PCS产生了错误的响应,User能够以100%的概率验证服务器返回的计算结果的正确性,因此算法GEXP的可验证概率为1.
证毕.
定理4.基于单个不可信的服务器模型,方案GEXP满足输入u,d和输出ud的隐私性.
证明. 在用户User请求服务器PCS的过程中,敌手能够获取到与底数u相关的信息为w1和w2,其中w1=uv1,w2=uv2,v1=gα,v2=gλ.v1和v2分别是子程序RandG产生的盲化随机对(形如(a,ga)随机、独立盲化对)中的一部分.底数u则由随机数v1,v2实现了隐藏.此外,用户User请求服务器PCS是以一种随机的方式进行的(请求计算数据对的顺序是任意的).因此,敌手不能获取到底数u的信息.
在我们的外包方案中,指数d可以被拆分为d=l1+k1t1,d=l2+k2t2.d由随机数t1,t2实现了隐藏,其中t1,t2长度通常至少是64 b.敌手通过猜测t1,t2恢复出d的概率是可以忽略的.因此,敌手同样不能获取到指数d的信息.
敌手可以获取到用户User请求服务器的PCS的数据对,但是通过这些数据并不能直接计算出最终的结果ud,并且已经证明了敌手不能获取到底数u和指数d的信息,也就无法通过u,d计算出ud.因此,敌手也不能获取输出ud的信息.
综上所述,方案GEXP满足输入u,d和输出ud的隐私性.
证毕.
4 性能分析
本节通过理论分析和实验模拟2方面对设计的幂指数运算外包方案GEXP的性能进行分析.
4.1 理论分析
我们将本文提出的方案GEXP分别与陈晓峰等人[7]、Wang等人[8]和任艳丽等人[13]提出的代表性幂指数外包方案进行了对比分析,其中Multi-plications表示乘法运算,Inversions表示求逆运算,Invoke(Rand)表示调用Rand次数,Invoke(PCS)表示请求服务器次数.表1给出了方案效率和结果可验证概率的对比.
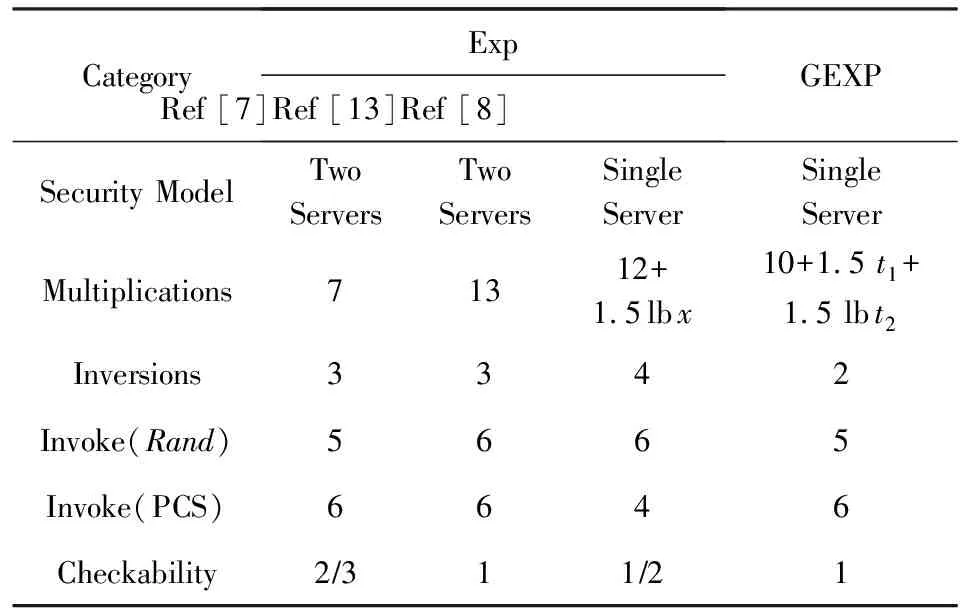
Table 1 Comparison of Exponentiation Outsourcing Schemes表1 指数安全外包方案对比
从表1可以看出,与文献[7-8]相比,方案GEXP在外包计算结果的可验证概率上有了很大的提升.在方案GEXP中,外包用户能够以100%的概率检测出服务器的不端行为,完全避免被服务器欺骗.虽然文献[7,13]在Multiplications方面要比方案GEXP和文献[8]小,其中文献[13]的可验证概率也达到了100%.但是文献[7,13]都是基于双服务器模型,可能遭受共谋攻击.此外,文献[8]与方案GEXP的Multiplications在开销方面受x,t1,t2等变量的影响.随着x,t1,t2等变量值的增大,用户的计算开销也会随之增大(在4.2节实验中会进一步分析).但与此同时,方案的安全性也会相应提高(d=c+bx,d=l1+k1t1,d=l2+k2t2),因为此时敌手更难猜测出d.
4.2 实验模拟
为了具体评估方案的性能,我们对本文提出的方案GEXP和文献[8]中的Exp方案进行了实验模拟.方案GEXP需要使用2台机器进行模拟,用户和服务器分别使用Intel Core i5 processors(1.20 GHz和2 GB内存)和Intel Core i5 processors(3.20 GHz和8 GB内存)进行模拟.使用的编程语言为Java语言.
图2给出了使用方案GEXP和直接计算群上的幂指数运算的时间开销对比.从图2中可以看出,方案GEXP的时间开销要远小于直接计算的时间开销,能够明显提升资源受限用户的计算处理能力.
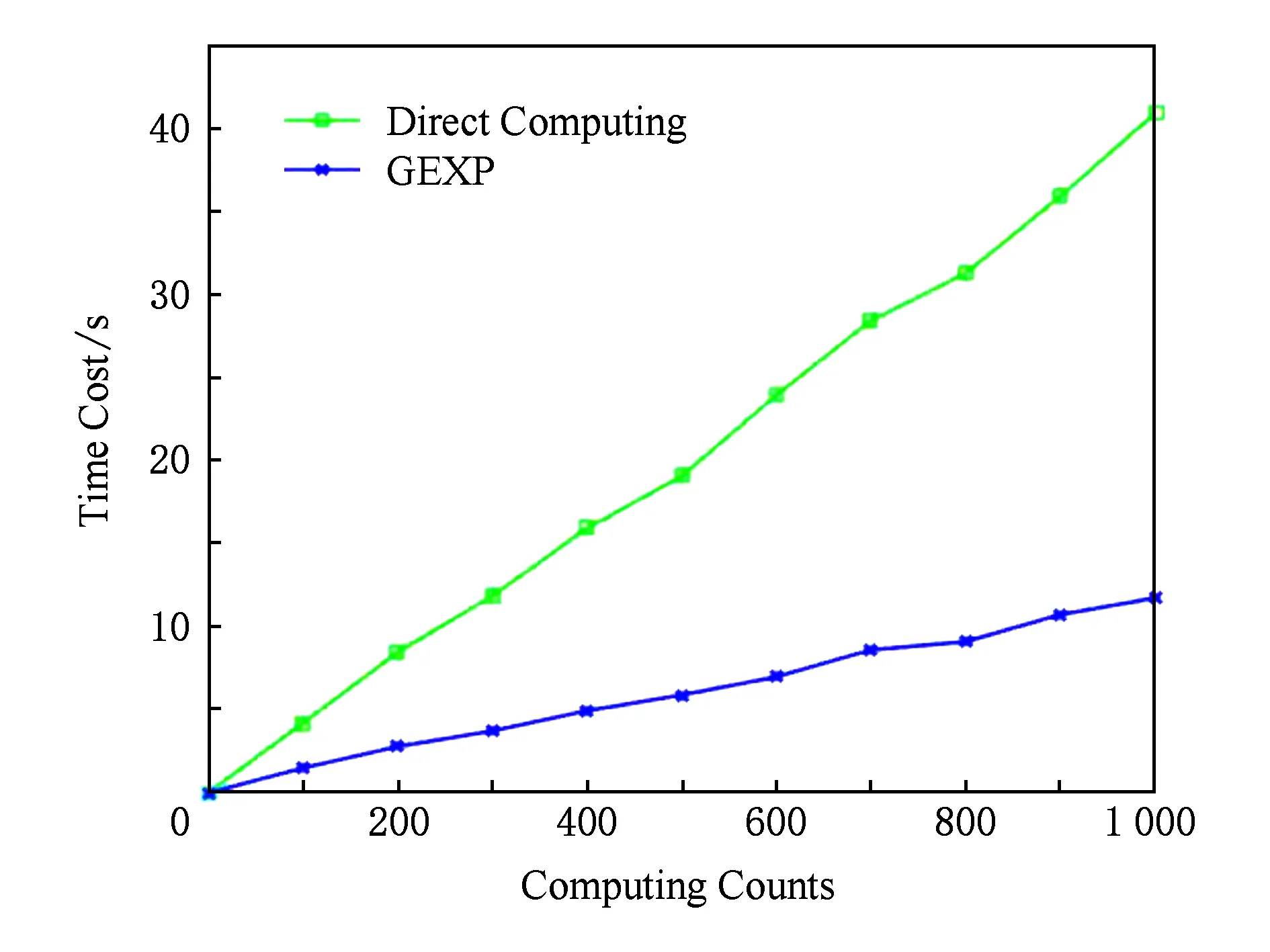
Fig. 2 Simulation of time cost for two schemes图2 2种方案的时间开销统计图
图3给出了在底数长度固定和指数长度变化时,方案GEXP和直接计算的时间开销对比.从图3中我们可以看出,不借助外包算法直接计算群上的指数运算时,其时间开销随着指数长度的增加呈现线性增长.当使用本文提出的外包计算方案GEXP时,时间开销会大幅度减小,并且时间开销基本上是固定的,不会随着指数长度的增加而增加.

Fig. 3 Time cost of ud (fixed base-variable exponent)图3 ud的时间开销统计图(底数固定、指数可变)
为了进一步评估我们所提出方案的性能,我们与同是基于单服务器模型的文献[8]中的Exp方案进行了实验对比分析.图4给出了分别使用方案GEXP、文献[8]中的Exp方案以及直接计算群上的幂指数运算的时间开销对比.从图4可以看出,方案GEXP和文献[8]中Exp方案的时间开销要远小于直接计算的时间开销,方案GEXP的时间开销要比文献[8]中Exp方案的稍大一些.这是因为方案GEXP牺牲用户少量时间换取了验证概率的大幅提升.此外,从图4我们可以看出,随着参数x,t1,t2的增大,方案GEXP和文献[8]中Exp方案的用户计算开销随之增大,但与此同时,方案的安全性也会提高.

Fig. 4 Simulation for different schemes图4 不同方案时间开销对比图
5 应 用
随着云计算的快速发展,企业用户和个人可以更经济、更方便地使用云端提供的数据服务,包括数据存储和数据共享等.但当用户将数据上传到云端后,他们失去了对数据的直接控制权,此时他们最关心的问题就是数据的完整性.可证明数据持有PDP是验证云端数据完整性的关键技术,该技术可以允许一个验证者去公开地验证用户存储在云端数据的完整性.但现有PDP方案中普遍需要涉及到群上的幂指数运算这一费时操作.
因此,我们使用所提出的方案GEXP去安全外包王博洋等人[25]提出的云端群组数据完整性验证方案Panda方案中的核心代理重签名HAPS.我们所提出的HAPS安全外包算法由6个子算法组成:
1) Initialize.令G1和G2是2个p阶循环群,g是G1的生成元,e:G1×G1→G2是一个双线性映射,ω是G1的另一个生成元.(e,p,G1,G2,g,ω,H)是系统的公开参数,其中函数H:{0,1}*→G1.
2) KeyGen.给定系统的公开参数(e,p,G1,G2,g,ω,H),用户uA选择一个随机数a∈输出公钥pkA=ga,并保持私钥skA=a私有.
3) ReKey.代理按照如下的方式生成重签密钥rkA→B:
① 代理产生一个随机数r∈并将该随机数发送给用户uA;
② 用户uA计算ra,并将计算后的结果发送给用户uB,其中skA=a;
③ 用户uB计算rba,并将计算后的结果发送给代理,其中skA=b;
④ 代理恢复重签密钥rkA→B=ba∈
4) Sign.给定私钥skA=a、数据块m∈p以及数据块标识id,对于数据块m上的签名,用户uA调用函数FGEXP,获取并输出:
σ=FGEXP(a,H(id)FGEXP(m,ω))=
FGEXP(a,H(id)ωm)=(H(id)ωm)a∈G1.
(10)
5) Resign.给定重签密钥rkA→B、公钥pkA、签名σ、数据块m∈p以及数据块标识id,代理核对如果验证结果为0,代理输出⊥;否则,代理调用函数FGEXP,获得并输出
σ′=σrkA→B=FGEXP(ba,σ)=
(H(id)ωm)a·ba=(H(id)ωm)b.
(11)
6) Verify.给定公钥pkA、数据块m、数据块标识id以及签名σ,验证者调用函数FGEXP,获取ωm=FGEXP(m,ω).如果e(σ,g)=e(H(id)ωm,pkA)成立,验证者输出1,否则输出0.
6 结束语
在本文中,基于单个不可信服务器模型,我们提出了一个新的群域上的幂指数运算安全外包方案GEXP,能够有效避免双服务器模型存在的共谋攻击问题.方案GEXP通过使用一种新的数学分割方法,用户可以将原始数据安全地分割成随机片的形式,从而保护了原始数据的隐私.与现有的方案相比,我们的方案GEXP在外包计算结果可验证概率上有了显著的提升,如果云服务器产生了任何不正确的响应,用户能够以100%的概率检测出错误.最后,针对云存储数据完整性保护方案中普遍涉及到大量群域上的幂指数运算问题,利用所提出的外包计算方案GEXP作为子程序实现了Panda方案的安全外包.

