目标成本值最优的物联网WSS蠕虫抑制算法
黄一才 周伟伟 郁 滨
(解放军信息工程大学 郑州 450001) (huangyicai3698@163.com)
作为互联网的发展与延伸,物联网技术将广泛应用于社会的方方面面[1-3].依据数据采集及传输方式,物联网可分为有线服务系统和无线服务系统(wireless service system, WSS).物联网WSS的实质是将最新的信息处理与通信技术进行有效的整合,利用各种感知设备和智能物体采集语音、图像、位置等数据信息,并通过无线通信方式将采集到的信息传递到资源平台进行云计算、数据挖掘等操作后,将处理与控制结果呈现给各用户终端[4-6].然而,由于WSS需要将大量感知设备和物体连接到应用系统中,而且这些设备和物品信息大多采用资源受限的无线传感器网络节点进行传输,这在增加系统灵活性和方便性的同时,为蠕虫在网络中的大规模传播提供了便利条件[7].蠕虫可以窃取被感染节点的隐私数据和敏感信息,同时伪造身份向邻居节点发送包含恶意代码的无线再编程指令,使感染蠕虫的节点数量不断增加.被感染节点可能导致系统大面积数据阻塞甚至瘫痪.感知设备中嵌入的大多数无线传感器节点具有资源有限的特性,如何最大限度地防御蠕虫在系统中的传播成为物联网快速发展的关键.目前,针对无线网络中蠕虫的研究主要是利用传统的流行病模型构建传播体系[8],在此基础上,分析不同网络参数对传播速率的影响[9].
许多分布式网络中的蠕虫传播及抑制方案这些年被相继提出以保护采集数据的安全性和隐私性.有线网络中经典的Kermack-Mckendrick参考模型将节点划分为3种不同的状态,利用控制参数和动力学微分方程描述蠕虫的传播速率,但仅将节点状态假设为易感状态,感染状态和恢复状态与WSS中IEEE 802.15.4协议不符[10].基于Markov链的传播模型通过引入节点半径与信道扫描的速率等参量求解各状态变量的微分博弈方程,但该方法未考虑WSS中基站控制节点休眠和唤醒转换概率的情况[11].基于细胞自动机的传播模型对多跳广播协议中的蠕虫病毒传播特点进行了模拟,但并未给出具体的防御和抑制方案[12].Bradley等人[13]提出了一种基于进程代数的复合主动蠕虫传播模型,通过PEPA流近似方法求解各状态的常微分方程.但该模型需要消耗大量系统资源,并不适用于节点资源受限的WSS.基于分层结构的异构网络蠕虫传播模型Enhanced-AAWP利用本地优先扫描蠕虫和随机扫描蠕虫等方法研究蠕虫的渗透传播过程[14].由于传统蠕虫传播模型中未考虑设备节点失效和休眠状态,因此,现有传播机制的分类并不适用于WSS.
高效的蠕虫分类机制是提高蠕虫传播模型准确性和防御策略效率的重要因素.为解决现有蠕虫分类准确性差的问题,朱克楠等人[15]基于朴素贝叶斯机器学习提出了利用行为序列报告和操作相似度窗口对蠕虫进行自动分类的方法.该方法为WSS蠕虫传播及抑制模型的进一步研究提供了有力支撑.
上述方案仅利用各种传播模型对蠕虫在不同网络环境下的传播特点和分类方法进行了分析,依据动力学原理获取不同节点的数据集,并未研究如何基于传播规律建立动态防御策略集抑制蠕虫在WSS中的传播.
快速准确的蠕虫检测方法是实现WSS动态最优策略防御的基础.近年来,一些学者通过降低噪声和网络随机事件的干扰,提出了许多基于行为序列的检测算法.毛蔚轩等人[16]利用节点休眠状态和基于人工经验的自适应学习方法,在分析网络拓扑中各层节点数据流依赖关系的基础上,给出了一种进程调用行为相似性与异常度结合的蠕虫抑制算法.该算法保证在已知少量蠕虫样本的条件下得到理想的检测率.文献[17]提出基于平均场法建立免疫模型,但该模型的抑制策略中没有休眠模式.针对混淆蠕虫攻击难以检测的问题,马洪亮等人[18]提出利用遍历抽象语法树(abstract syntax tree, AST)和单等级支持向量机(one class support vector machine, OC-SVM)检测混淆并跟踪节点相关的变量终值检测反混淆.Das等人[19]用频繁项离群确定同源度,并对同源判定阈值进行预定义,进而实现蠕虫的同源判定.郭洋河等人[20]将数据和行为依赖关系相结合,提出了一种基于造价序列库的蠕虫识别机制.文献[21-22]利用挂钩API的方法追踪外部节点的访问行为,改善了动态检测方法执行路径单一的问题.这些检测方法对蠕虫的检测成功率较高,但缺少与WSS匹配的蠕虫最优防御算法.
在现有的蠕虫检测策略条件下,如何设计最优防御算法是WSS在高安全领域应用的关键.文献[23]指出可以将蠕虫防御问题转化为动态博弈纳什均衡的求解问题.Mishra等人[24]引入攻击方的类型概率和收益矩阵,通过判断贝叶斯博弈中收益函数值选取最优动作集合,但该方案不能实时校正外部节点的后验概率.Pandey等人[25]将蠕虫和系统的攻击防御转化为二者的最优化博弈问题,提出基于僵尸网络环境的流行病模型以及微分博弈机制,在考虑防御策略及恶意软件参数限制的基础上给出了动态博弈的闭环纳什均衡解.该方案虽然得到了微分博弈最优解,但未讨论隔离状态对其他网络状态的影响.这些方案虽然对蠕虫在无线网络中的传播及抑制进行了一定程度的研究,但并未考虑WSS中基站能够使易感节点免疫,同时可以广播补丁程序治愈已感染节点.
结合WSS中的网络参数及节点状态特点,仍需重新建立传播模型及基于时间特性的动态微分博弈模型,在满足网络参数约束条件的情况下,有效抑制蠕虫在网络中的传播并使系统的安全成本最低.
本文的贡献是构建一个描述物联网WSS蠕虫传播规律的流行病模型和蠕虫防御动态微分博弈模型,求解最优策略控制集合的取值并给出了抑制蠕虫传播的防御算法.具体地,本文主要得到3个方面的结果:
1) 依据物联网中WSS的网络拓扑结构,对蠕虫攻击下设备节点之间的状态转换过程进行分析,给出了WSS状态转换图和各状态微分方程,利用通信半径确定具有感染能力的节点区域和数量并构建改进的流行病模型.
2) 建立蠕虫和WSS间的动态微分博弈模型,通过目标成本函数量化攻击方和防御方不同决策所得到的成本支付.
3) 利用汉密尔顿函数、瞬时成本函数以及终期成本函数的线性条件证明了动态微分博弈鞍点的存在性.结合成本函数与汉密尔顿函数的最小化极值特点,求解蠕虫传播的最优防御策略并给出了具体算法.
1 基础知识
1.1 WSS系统结构
随着物联网在各个领域的快速发展,其安全问题越来越受到重视,尤其是对信息安全性和隐私性要求较高的WSS中.WSS大多采用无线传感器网络技术实现各节点之间的数据与图像传输、数据处理、实时控制等.无线信道的开放性和节点的同构性使恶意软件很容易在网络中大面积传播.
物联网WSS的系统结构如图1所示.该系统的目标是保证无论何时、何地、任何媒体设备的实时连通性和可控性.其结构主要包括无线传输系统、数据采集系统和终端用户系统.由于WSS设备的移动性和采集数据分布范围广的特点,无线传感器网络技术在WSS数据采集和传输中的应用较为普遍.但嵌入无线传感器网络节点的设备一旦被蠕虫感染,极易在网络中传播.这些被感染的节点对系统数据的机密性、隐私性和完整性构成了巨大威胁.
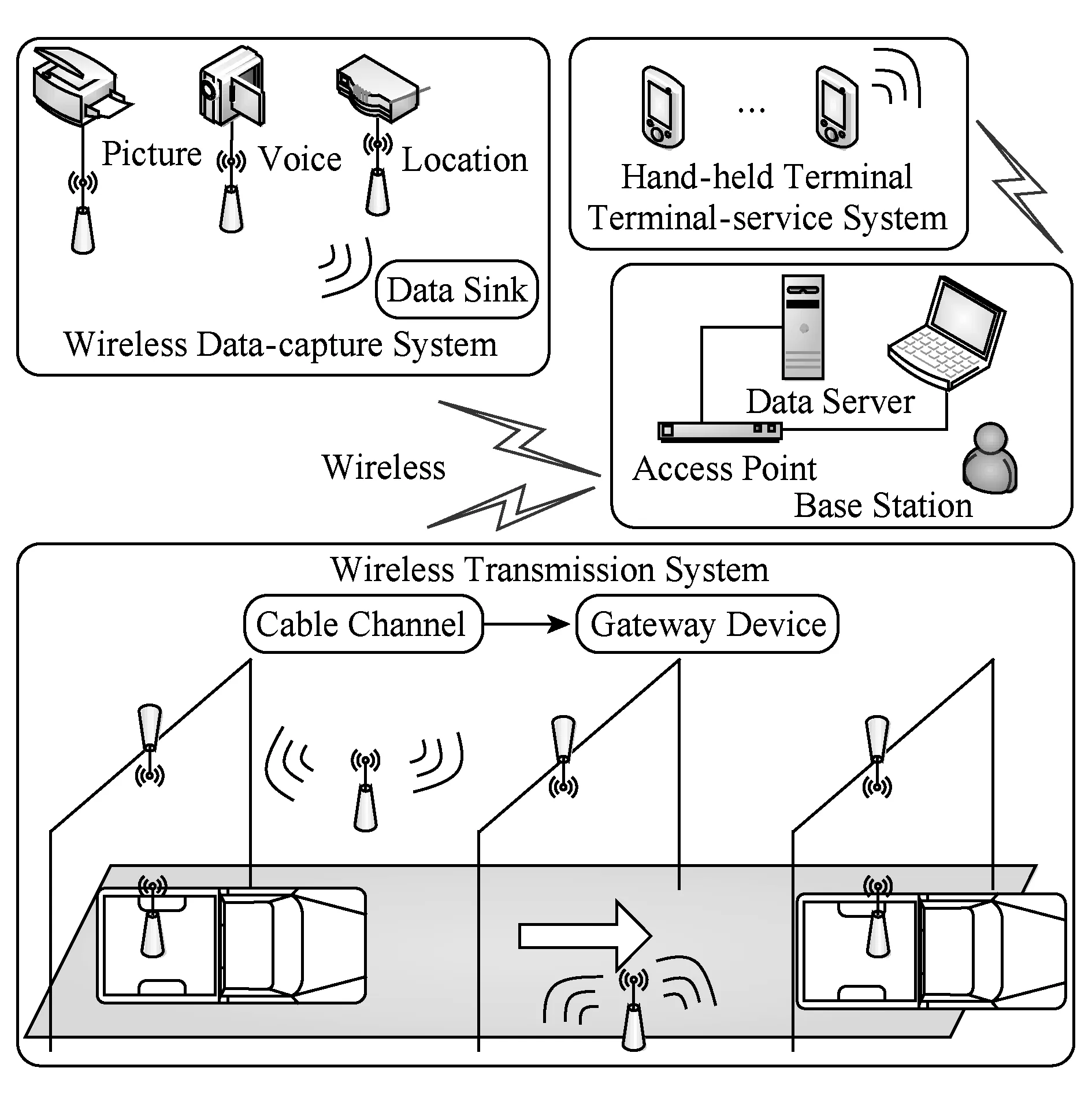
Fig. 1 System structure of WSS in IoT图1 物联网WSS的系统结构
1.2 网络链路模型
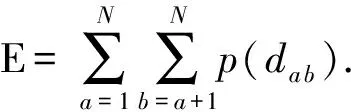
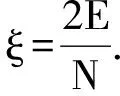
(1)
节点间存在链接的概率p(da b)由WSS中的无线电通信机制以及节点间的通信半径决定.信号发射端与信号接收端通过阈值判定模型确定节点间是否存在通信链路[26].
1.3 传统流行病模型
流行病模型最早是用于预测和描述具有传染性因素特征的部分人员集合随时间实时变化的态势.这些因素特征包括网络节点的发送率、接收率、传播速率等.依据不同网络的特点,现有流行病模型分为SI[27],SIS[28],SIR[29]模型.
通常情况下,网络中感染节点注入安全补丁可以转变为恢复状态.因此,SIR模型更适用于具有安全补丁的网络流行病传播特点.S(t),I(t),R(t)分别代表在时刻t易感节点、感染节点和免疫节点的数量.假设网络中各节点之间存在通信链路,令α为蠕虫感染速率,β为免疫速率,则描述各状态节点变化速度的微分方程为
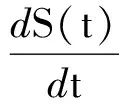
分析其他网络模型时,可以依据经典SIR模型和具体的网络协议进行分析和求解.
1.4 蠕虫攻击模型
WSS中传播的蠕虫主要指被动型蠕虫.假设WSS中源节点的安全认证机制失效,蠕虫控制该节点并获取认证密钥.感染节点利用签名密钥对嵌入蠕虫字段的再编程命令帧签名并发送到邻居节点.其他邻居节点收到伪装的命令帧后验证认证机制,更新配置并执行相应操作.蠕虫在WSS节点间通过多跳的形式向外传播.感染节点采集和传输的数据遭受窃听、篡改和破坏.
2 WSS系统模型
2.1 状态转换
WSS中的蠕虫传播可以用包含易感节点、感染节点和免疫节点的区域来表示.不同状态节点的分布如图2所示.由于免疫节点在全网均匀分布,因此,未在系统模型中标出.
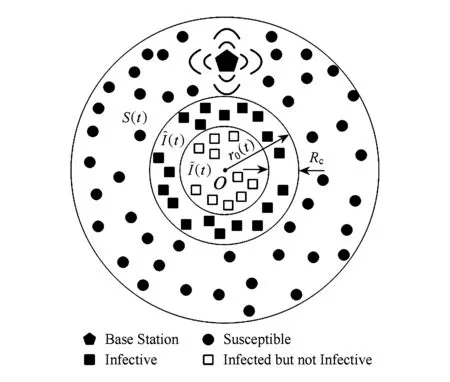
Fig. 2 System model of WSS图2 WSS系统模型
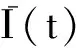
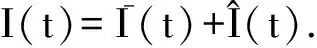
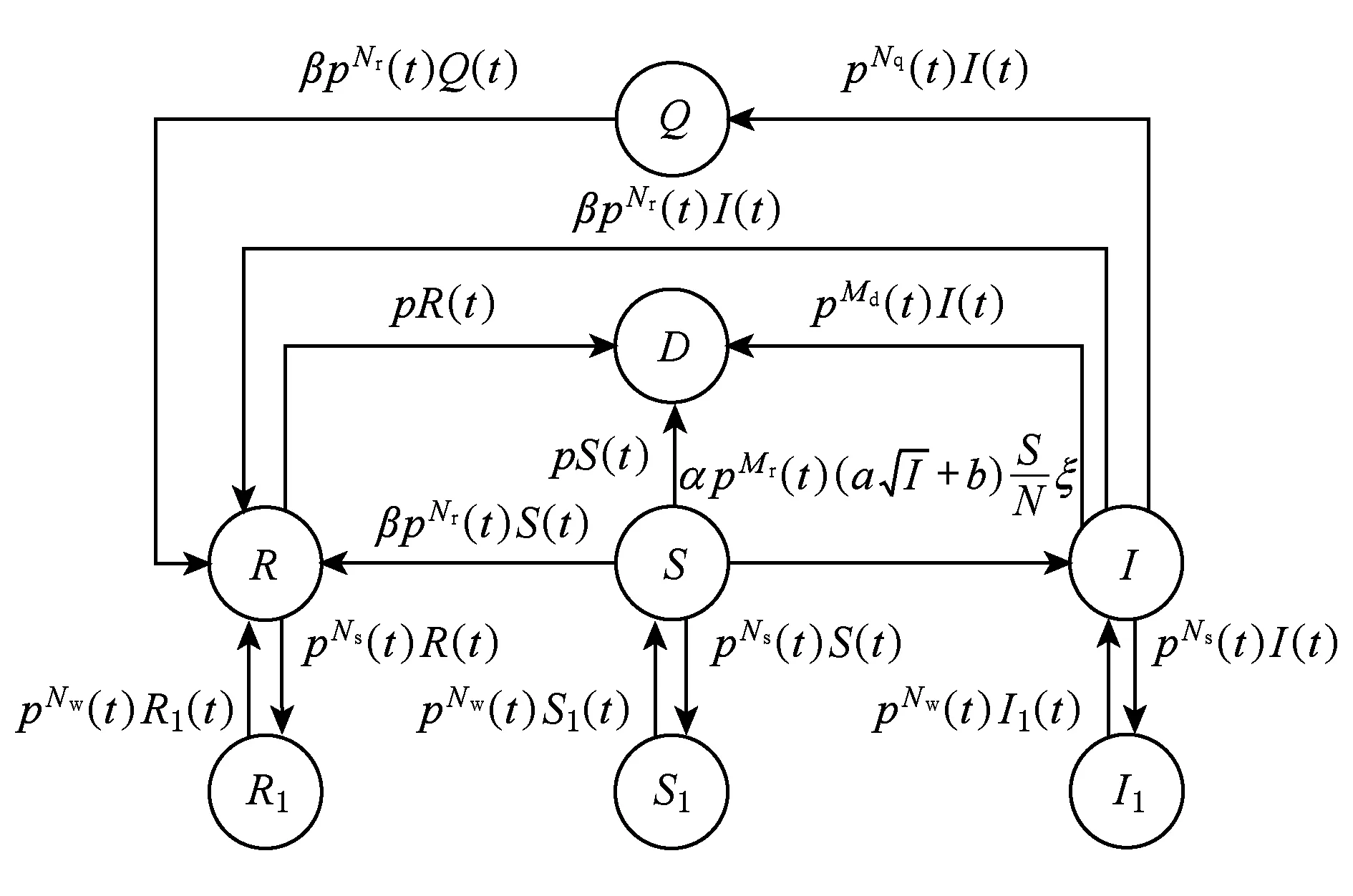
Fig. 3 State transition diagram of nodes in WSS图3 WSS节点状态转换图
依据WSS的特点,节点可分为8种不同的状态,各状态之间的转换关系如图3所示:
1)S.处于状态S的节点为易感节点,即易遭受蠕虫感染,但目前仍处于正常工作状态.
2)S1.处于状态S1的节点是状态S的休眠节点,由于节点处于休眠状态时停止收发数据,该状态的节点不会被蠕虫感染.
3)I.处于状态I的节点为感染节点,蠕虫可以窃取节点存储、处理、传输的数据,同时能通过该节点感染其他易感节点.
4)I1.处于状态I1的节点为感染节点I的休眠节点,该状态的节点失去通信功能,无法感染其他易感节点.
5)Q.处于状态Q的节点为系统通过安全规则检测并隔离的节点,该状态的节点无法感染其他易感节点.
6)R.处于状态R的节点为植入安全补丁后获得对蠕虫免疫状态的节点.
7)R1.处于状态R1的节点为状态R的休眠节点.
8)D.处于状态D的节点为失效节点,节点失去通信和数据处理功能.
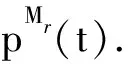
8种不同状态的节点满足:
N=S(t)+I(t)+R(t)+S1(t)+
I1(t)+R1(t)+D(t)+Q(t).
(2)
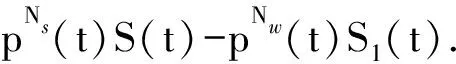
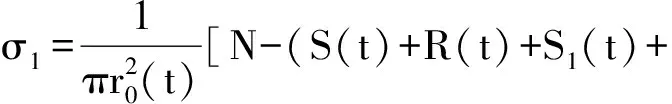
(3)
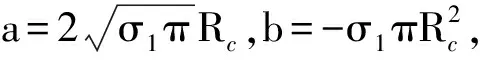
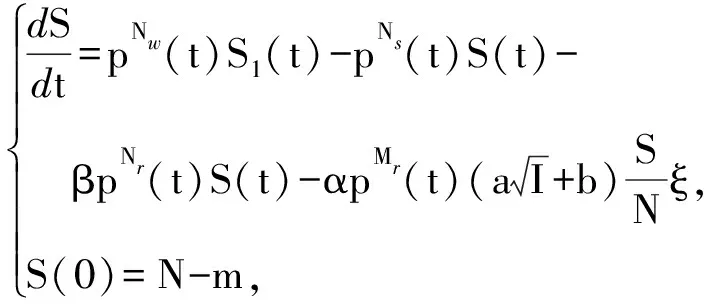
(4)
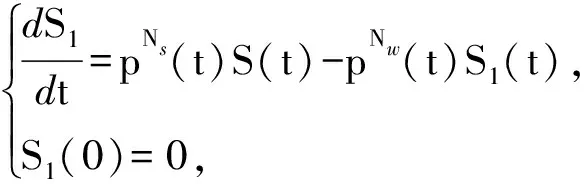
(5)
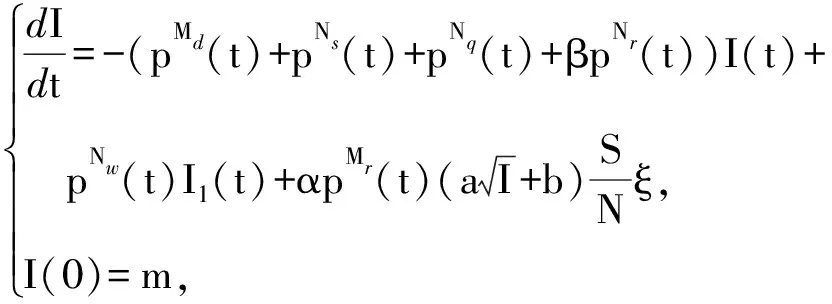
(6)
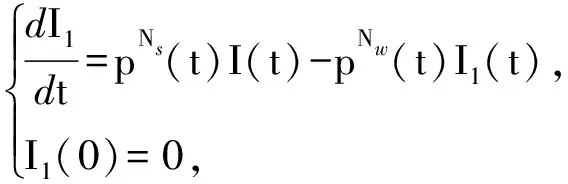
(7)
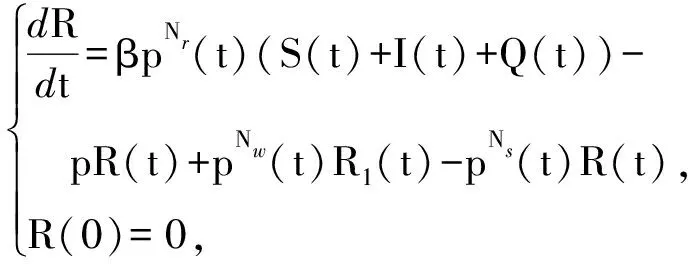
(8)
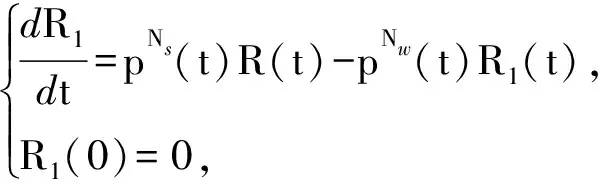
(9)
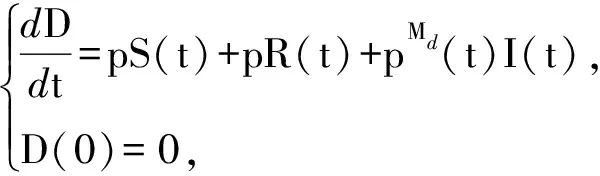
(10)
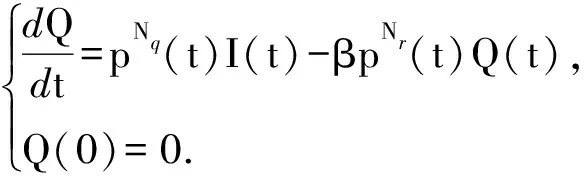
(11)
2.2 博弈模型
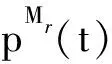
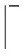
1)N={蠕虫A,WSSD}是一个包含2个参与者的集合;
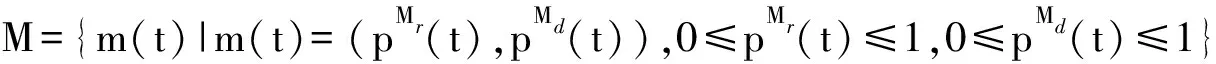
3)F={f(t,r(t),m(t),s(t))|fS,fI,fR,fS1,fI1,fR1,fQ,fD},其中f(t,r(t),m(t),s(t))是一个随时间连续变化的状态函数,r(t)=(S(t),I(t),R(t),S1(t),I1(t),R1(t),Q(t),D(t))是一个8维的状态变量,其中,
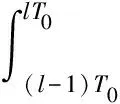
在定义1中,博弈双方分别为蠕虫A和WSSD,WSS通过调整防御策略S使目标成本函数J的值达到最小,而蠕虫通过攻击策略M保证J的值达到最大,该博弈模型为动态完全信息零和微分博弈,即攻击方和防御方均知道对方采取每个策略的支付.
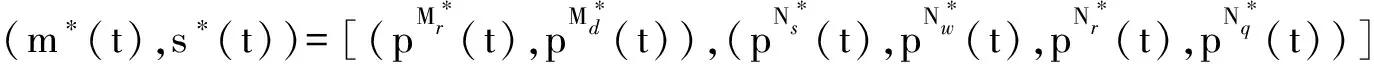
J(m(t),s*(t))≤J(m*(t),s*(t))≤J(m*(t),s(t)).
令V=J(m*(t),s*(t)),当攻击方选择策略m*(t)时,无论防御方采取何种防御措施,成本函数的值至少为V;当防御方采取策略s*(t)时,成本函数的值至多为V.当系统采取鞍点策略时,满足关系V=V0=V1.
由于成本函数J与WSS的QoS相关,被蠕虫感染的节点数据的机密性和隐私性遭到破坏,且影响节点的正常工作,节点持有的内部资源被非法调用和读取,定义此时蠕虫在感染节点集合中引起的瞬时成本为μII(t),其中μI为协议中感染节点的瞬时成本相关系数.失效节点的增加会导致网络中路由路径发生改变,部分数据无法正常采集和传递,使成本函数值增加,由此,定义失效节点的瞬时成本为μDD(t),μD为失效节点的瞬时成本相关系数.同理可得,恢复节点的瞬时成本为μRR(t),隔离节点的瞬时成本为μQQ(t),休眠节点的瞬时成本函数分别为μS1S1(t),-μI1I1(t)和μR1R1(t).
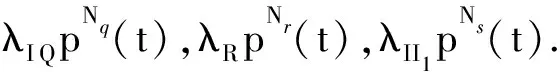
由以上分析可得,定义1中的成本函数可表示为
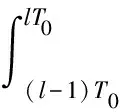
(12)
为了求解博弈K的鞍点策略,首先需要分析该博弈的鞍点是否存在.
定理1. 如果WSS中蠕虫防御微分博弈满足定义1及其约束条件,那么该博弈存在使系统达到最优的鞍点策略.
证明. 微分博弈存在鞍点策略必须满足4个条件:
1) 系统的状态函数在各状态和控制策略上是连续且有界的;
2) 在成本函数中,瞬时成本和终期成本在各状态和控制策略上是连续的;
3) 状态函数和瞬时成本函数是由控制策略线性表示的,且博弈中定义的控制策略集合均是凸的;
4) 攻击方和防御方的控制策略是有界的.
由定义1可知,状态函数f(t,r(t),m(t),s(t))是连续的且其各状态变量的取值由式(4)~(11)确定,M和S对控制策略的上下限进行约束,因此,状态函数在各状态和控制策略上是连续且有界的,条件1显然满足.瞬时成本和终期成本随着各状态和控制策略的增加而线性增加,其在各状态和控制策略上是连续的,满足条件2.由式(4)~(12)可知,状态函数和瞬时成本函数均由控制策略线性表示,且控制策略集合中的参数可在连续区间内取值,故博弈中控制策略集合是凸的,满足条件3.由协议中控制策略的约束条件可知,条件4显然满足.
因此,博弈K存在使系统性能达到最优的鞍点策略.
证毕.
3 博弈模型的求解
本节以动态微分博弈K的目标成本函数最小为求解依据,通过引入汉密尔顿函数,将目标成本函数最小问题转化为判定双方策略参数对应系数的正负问题.在此基础上,结合状态函数和初始状态值,求解不同系数范围下的最优控制策略.
由于参与者双方的控制策略参数取值是一个连续的取值空间,博弈模型的最优策略求解无法通过线性分析和分类数值对比实现,且参数取值的无限特性使函数的凸性分析无法直接求解.因此,引入汉密尔顿函数作为对目标成本函数和各策略控制参数进行定量分析的工具,简化最优控制策略的求解问题.
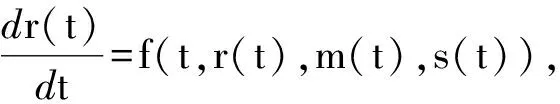
由于动态博弈存在鞍点策略,可以利用目标成本函数的性能泛函构建汉密尔顿函数,其协状态函数可表示为
κ(t)=(κS(t)κI(t)κR(t)κS1(t)κI1(t)
κR1(t)κQ(t)κD(t))T.
利用拉格朗日乘子法,构造新的增广泛函:
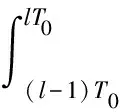
(13)
其中,κ(t)为8维的拉格朗日乘子系数矢量.纯量函数H可表示为
H[t,κ(t),r(t),m(t),s(t)]=w(t,r(t),m(t),s(t))+
κ(t)f(t,r(t),m(t),s(t)).
(14)
H[t,κ(t),d(t),m(t),s(t)]为构造的汉密尔顿函数,则式(13)可简化为
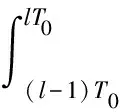
(15)
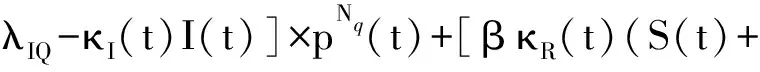
(16)
由式(15)展开欧拉方程可导出上述泛函极值的必要条件为
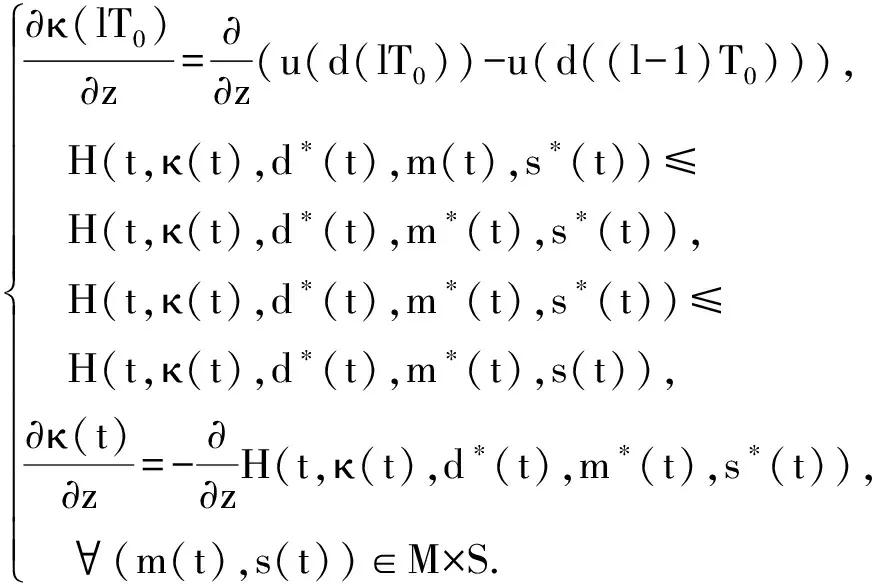
由式(12)和式(14)可得汉密尔顿函数如式(16)所示.
设汉密尔顿函数中各策略控制参数的系数分别为
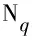
可得:
(17)
依据汉密尔顿函数以及泛函极值的必要条件,可得协状态函数的微分方程及极值,进而结合相应的初始条件得到协状态函数κ(t)中的8个空间向量值,将其代入到式(17)可求解各策略控制参数的系数.
定理2. 如果蠕虫与WSS之间的微分博弈满足定义1,那么在动态微分博弈K中攻击方蠕虫A的最优控制策略为
防御方WSSD的最优控制策略为
证明. 由于汉密尔顿函数可表示为策略控制参数与相应系数的线性表达式,且泛函极值的必要条件中要求WSS中蠕虫动态防御最优策略的鞍点必须满足:
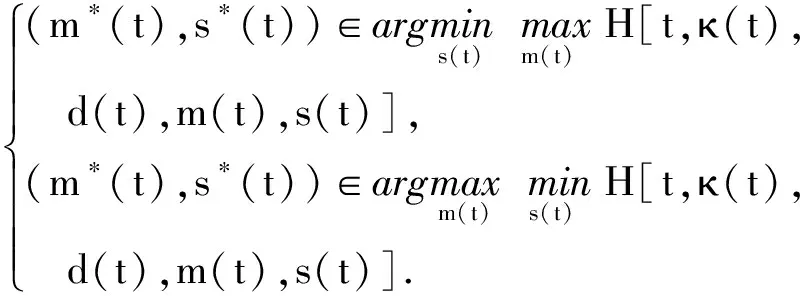
因此,当WSS策略控制参数相应的系数大于0时,策略控制参数取约束范围内的最小值,反之取最大值.当蠕虫策略控制参数相应的系数大于0时,策略控制参数取约束范围内的最大值,反之取最小值.
证毕.
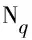
4 动态防御最优策略算法
依据第l个博弈阶段的状态节点数量初始值、状态函数、协状态函数以及各控制策略系数,由协议计算使蠕虫动态防御最优的鞍点策略.该防御机制主要包括4个部分:参数存储模块(parameters storage module)、安全管理中心(security manage-ment center)、蠕虫A(wormA)、WSSD.在此基础上,设计适应于WSS的蠕虫动态防御最优策略机制如图4所示:
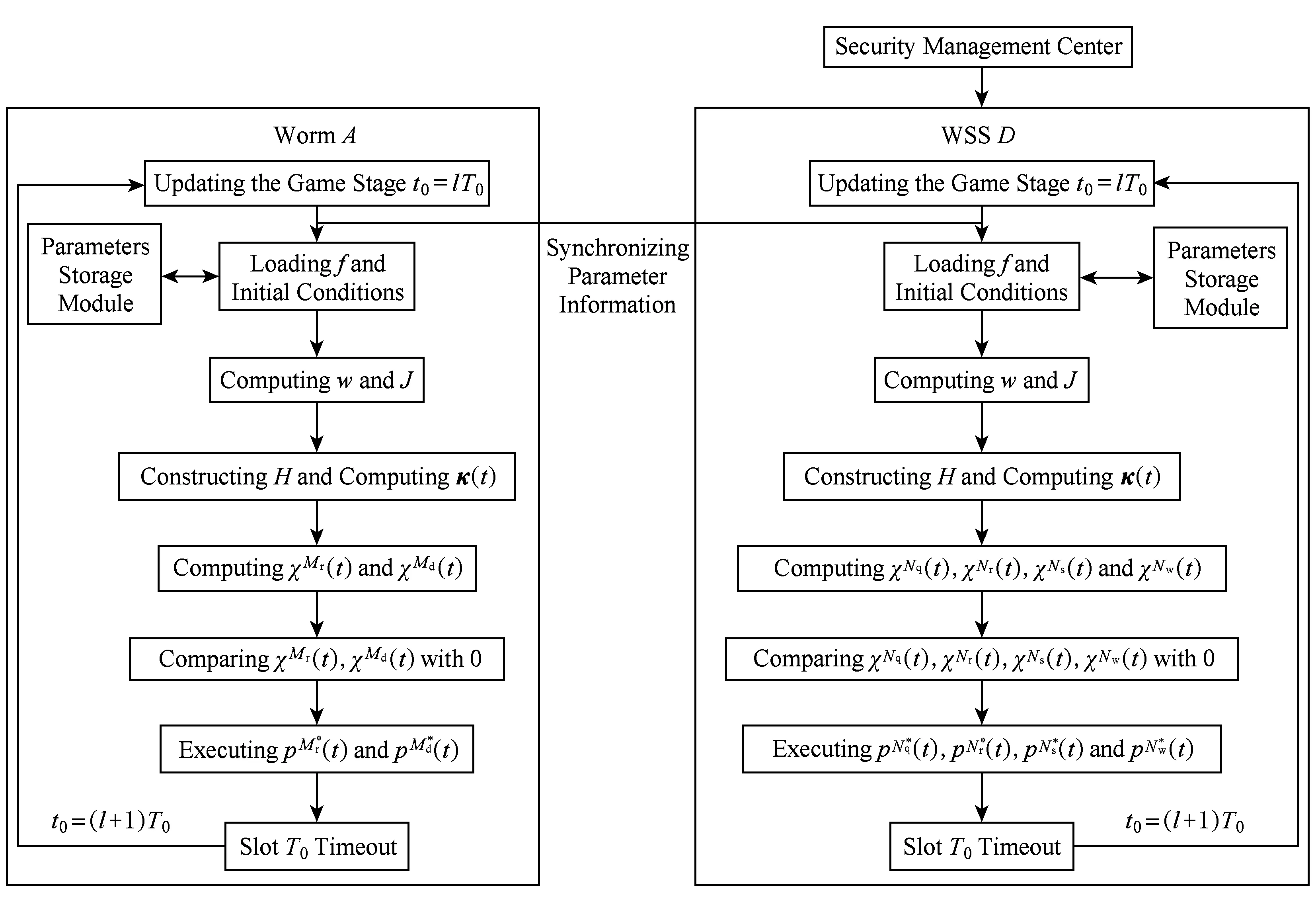
Fig. 4 Optimal defense strategy against worm propagation based on modified epidemic model图4 基于改进流行病模型的蠕虫动态防御最优策略机制
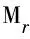
本方案中基于目标成本值最优的蠕虫传播最优攻击算法和最优防御算法如下:
算法1. WSS蠕虫传播最优攻击算法.
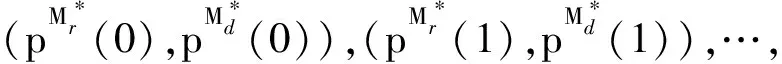
Step1. 初始化式(4)~(11)的假设条件,设置时间窗t=1,判断是否满足t≤k.若满足条件,则利用状态微分方程求解该博弈阶段的各状态值;否则跳转到Step5.
Step2. 结合攻击方和防御方控制参数初始值以及协状态微分方程,将时刻lT0的协状态值代入求解不同博弈阶段的协状态值κS(t),κI(t),κR(t),κS1(t),κI1(t),κR1(t),κQ(t),κD(t).
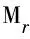
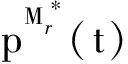
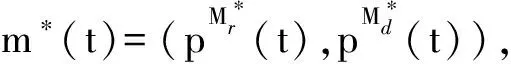
算法2. WSS蠕虫传播最优防御算法.
输入:控制参数初始值及博弈阶段起点t=1;
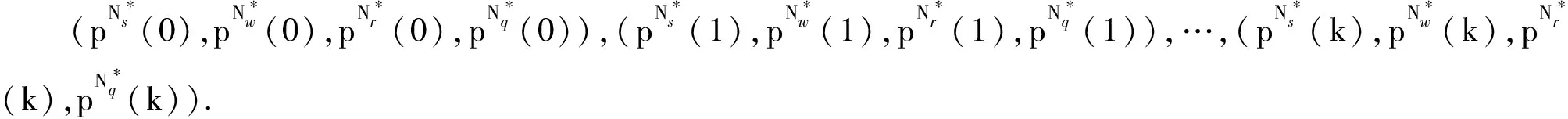
Step1. 设置初始时间窗t=1,配置初始化参数并由状态微分方程求解各博弈阶段状态值,判断是否满足t≤k,若满足执行下一步操作;否则跳转到Step5.
Step2. 加载博弈中参与者的控制参数初始值以及协状态微分方程,将时刻lT0的协状态值代入求解不同博弈阶段的协状态值.
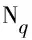
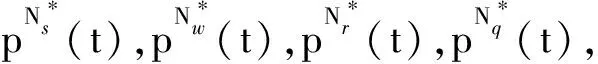
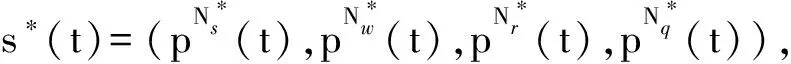
5 实验与结果分析
5.1 实验设计
本实验在HP Z238工作站(3.2 GHz 8核心超线程、8 GB内存、Windows XP)上实现,使用的WSS网络仿真平台是NS-2,NS-2是由UC Berkeley开发的面向对象的无线网络仿真模拟器.它通过设置虚拟时钟并逐个执行离散事件完成算法的运行.从VXHeaven中抽取5个蠕虫样本并随机选取一种作为WSS蠕虫攻击源.
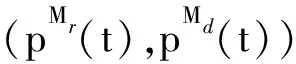

Table 1 Parameter Configuration in NS-2表1 NS-2参数设置
NS-2配置细胞自动机算法[12]的类型为混沌型,采用诺伊曼细胞空间对网络节点进行编号,节点i的状态为Si∈{1,2,3,4,5,6,7,8},该节点的2邻居状态分别为(Si-1,t)和(Si+1,t),利用转换规则函数表切换各节点状态.
Enhanced-AAWP扫描算法[21]中蠕虫实例的平均扫描速率为η=7,一个扫描时间单元的长度为60 s,系统采取随机扫描和本地扫描的概率分别为P1=0.875和P2=0.125.
在上述网络环境下运行细胞自动机算法[12]、Enhanced-AAWP扫描算法[21]和本文算法,利用NS-2中的State sniffer进程追踪并统计各状态节点以及策略参数的变化情况,结合MATLAB 2010a对实验结果进行数值分析.通过仿真实验对比这3种算法在WSS蠕虫防御方面的性能差异.
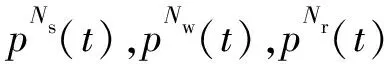
5.2 方案性能测试
通过仿真环境实现文献[12,21]中的方案及初始条件,对比不同状态节点所占比例随时间的变化曲线.为了得到更加精确的结果,重复实验20次并取所有结果的平均值.
如图5所示,在文献[21]中,网络模型通过Enhanced-AAWP随机扫描和本地扫描蠕虫,未考虑休眠节点和隔离节点对策略均衡的影响,导致在计算防御策略的阈值时存在较大误差,S和I的实验测定值与文献[21]中均衡方程的计算值误差超过6%.在第1个博弈阶段,算法中防御参数的切换延迟,易感节点所占的比例迅速下降.感染节点所占比例在第43个博弈阶段达到最大值.随着恢复节点所占比例的增加,感染节点缩小对周围节点发送蠕虫命令帧的数据量,开始执行使感染节点转变为失效节点的策略.该方案在建立脆弱性主机自治系统的全局可达网络时假设状态为I的节点均有蠕虫传播能力,而感染节点区域内距离外部易感节点距离超过Rc的感染节点不具备感染能力.在最终平衡态时易感节点的比例保持在2.19%~3.06%,由感染节点转变为失效节点的比例为32.29%,方案的均衡策略不能达到实际的最优抑制效果.
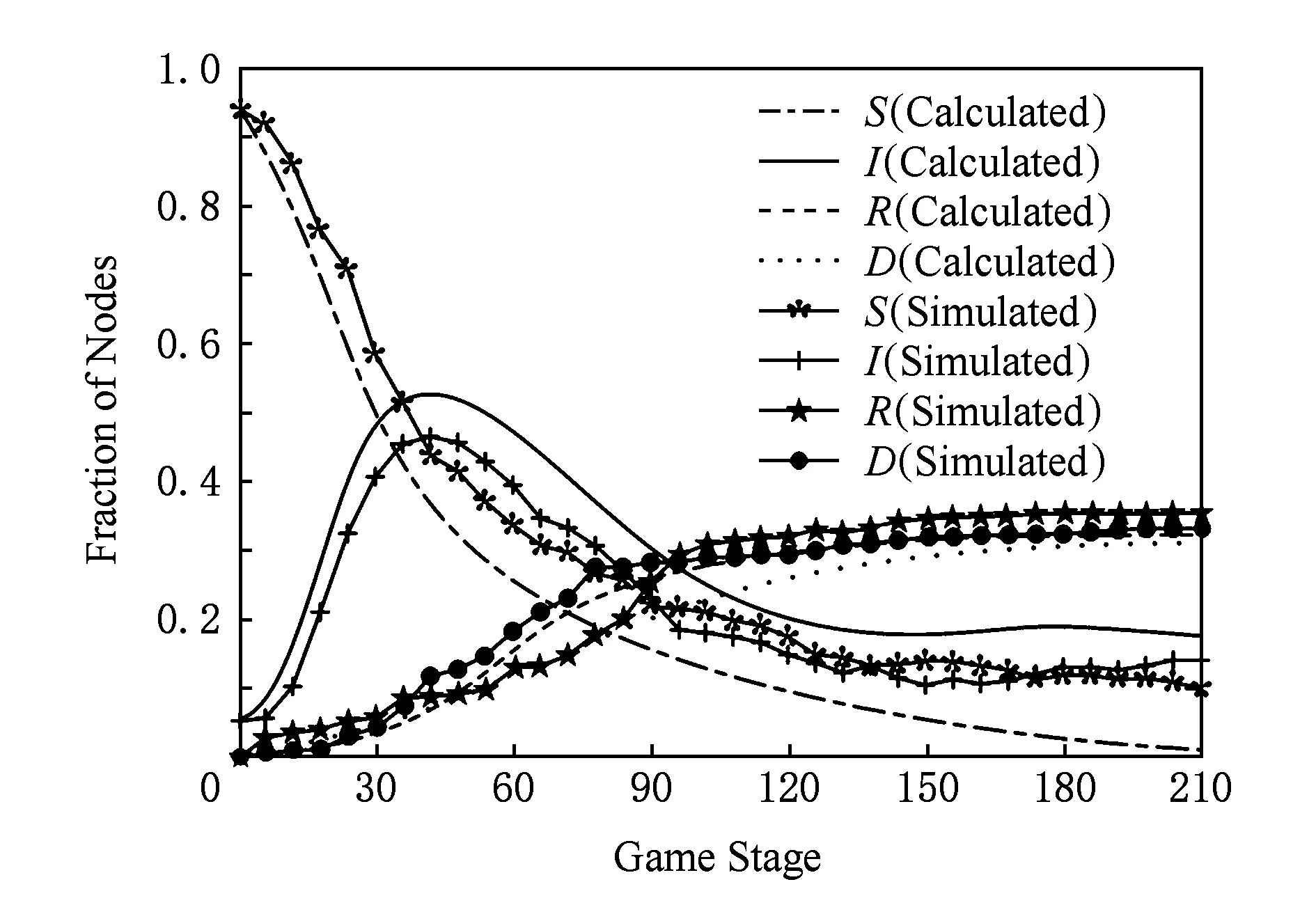
Fig. 5 Fraction curve of nodes in each state of Ref [21]图5 文献[21]中各状态节点曲线
与文献[21]相比,文献[12]在建立网络模型时考虑了靠近感染节点区域内侧时无法与外侧易感节点通信的情况,但在流行病模型的计算中未引入休眠节点和隔离节点的微分方程.如图6所示,易感节点所占比例在整个博弈阶段明显优于文献[21].当博弈结束时,易感节点所占比例的稳态值7.69%大于文献[21].感染节点所占比例的曲线波峰到来的时间迟于文献[21].失效节点增加的速度有所减小,且稳态时所占比例保持在21.31%,低于Enhanced-AAWP中的32.29%,由于休眠节点和隔离节点对蠕虫传播具有抑制作用,该方案将这2种节点均作为易感节点进行数值计算,防御策略的参数取值时间不够准确.失效节点和感染节点所占比例均超过18%.
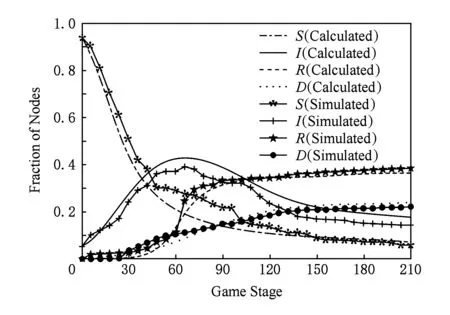
Fig. 6 Fraction curve of nodes in each state of Ref [12]图6 文献[12]中各状态节点曲线
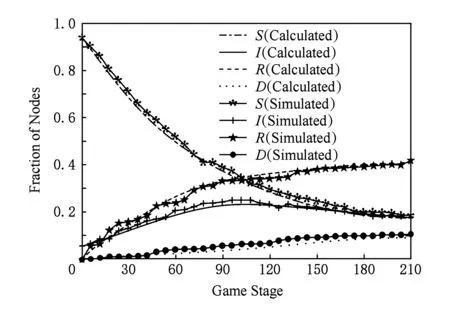
Fig. 7 Fraction curve of nodes in each state of this paper图7 本文中各状态节点曲线
本文方案中各状态节点所占比例的理论值与仿真计算值如图7所示.动态防御最优策略算法在S-I-R动力学模型的基础上添加了休眠状态(S1,I1,R1)以及安全隔离状态(Q),且利用Rc=50及式(3)计算了具备蠕虫传播能力的感染节点.易感节点在稳态时的比例保持在19.17%~20.62%,失效节点的比例在整个博弈阶段低于10%,感染节点比例控制在17.29%~18.06%.感染节点的比例在第96个博弈阶段时达到最大值22.17%,远低于其他防御策略.从第96个博弈阶段开始,基站向网络中发送大量安全补丁,同时大量节点处于休眠状态阻止蠕虫在系统中的传播,因此,恢复节点的比例并未迅速增长.与上述2种方案相比,改进流行病模型得到的鞍点策略在蠕虫传播方面具有更好的抑制效果.
State sniffer采集到的数据代入式(12)得到各算法目标成本值随时间的变化情况,如图8所示.I(0)=120的目标成本值不到I(0)=240的目标成本值的40%,这是由于达到均衡时I(t)和D(t)在目标成本值中所占比例
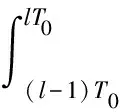
较大.随着博弈阶段的更新,当I(0)=120和I(0)=240时,本文算法在各阶段达到策略均衡时的目标成本值均远小于其他算法,且差值逐渐扩大.基于改进流行病模型和目标成本值最优的抑制算法在WSS蠕虫传播防御方面具有明显优势.
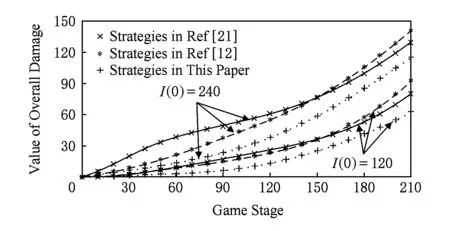
Fig. 8 Comparison of target costs in different strategies图8 不同策略下的目标成本值对比
5.3 参数分析

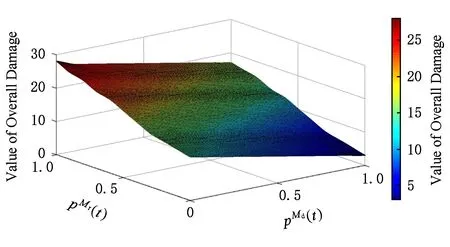
Fig. 9 Target cost under different and 图9 不同和下的目标成本值
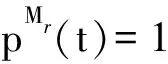
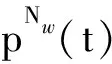
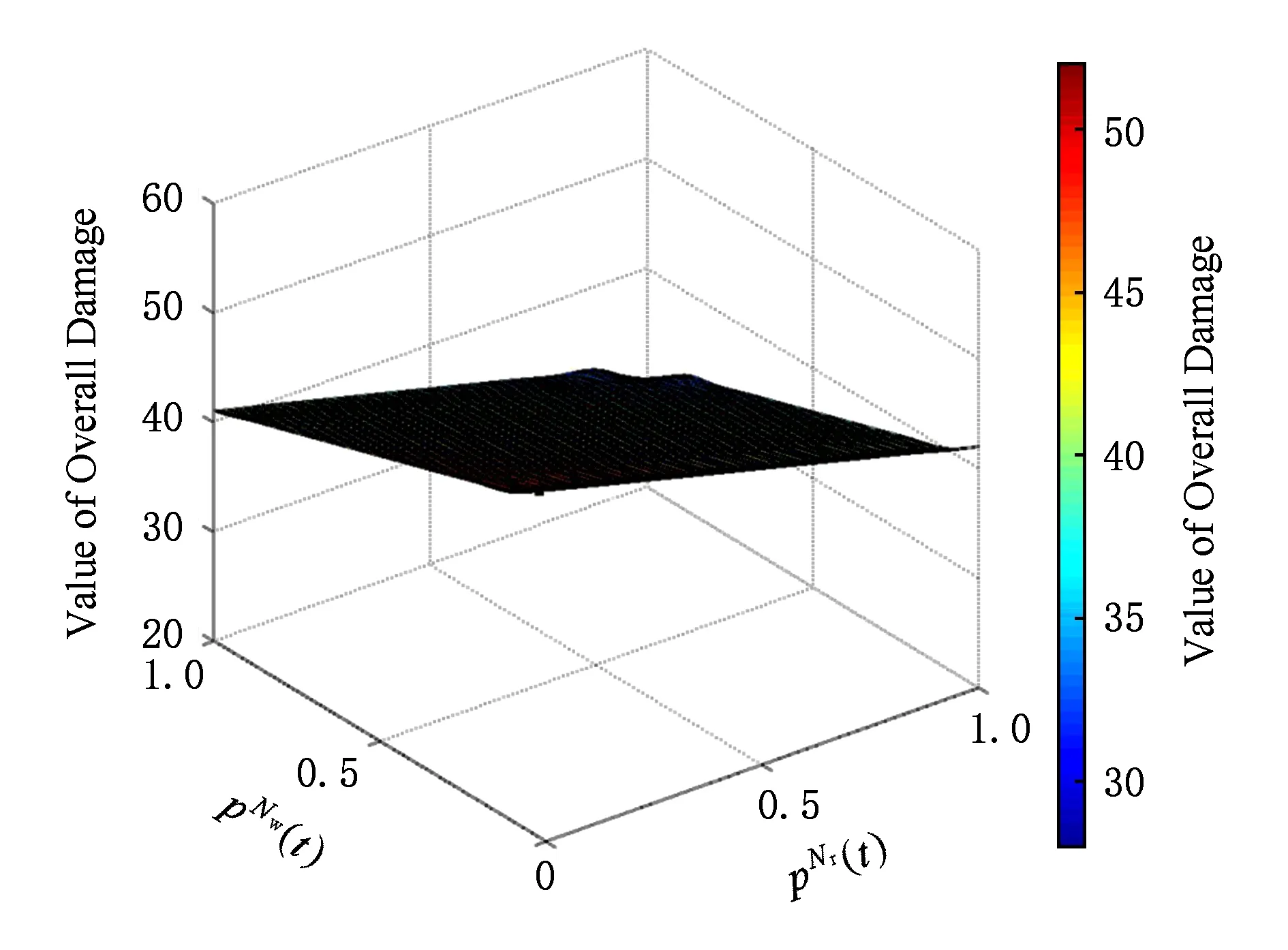
Fig. 10 Target cost under different and 图10 不同和下的目标成本值
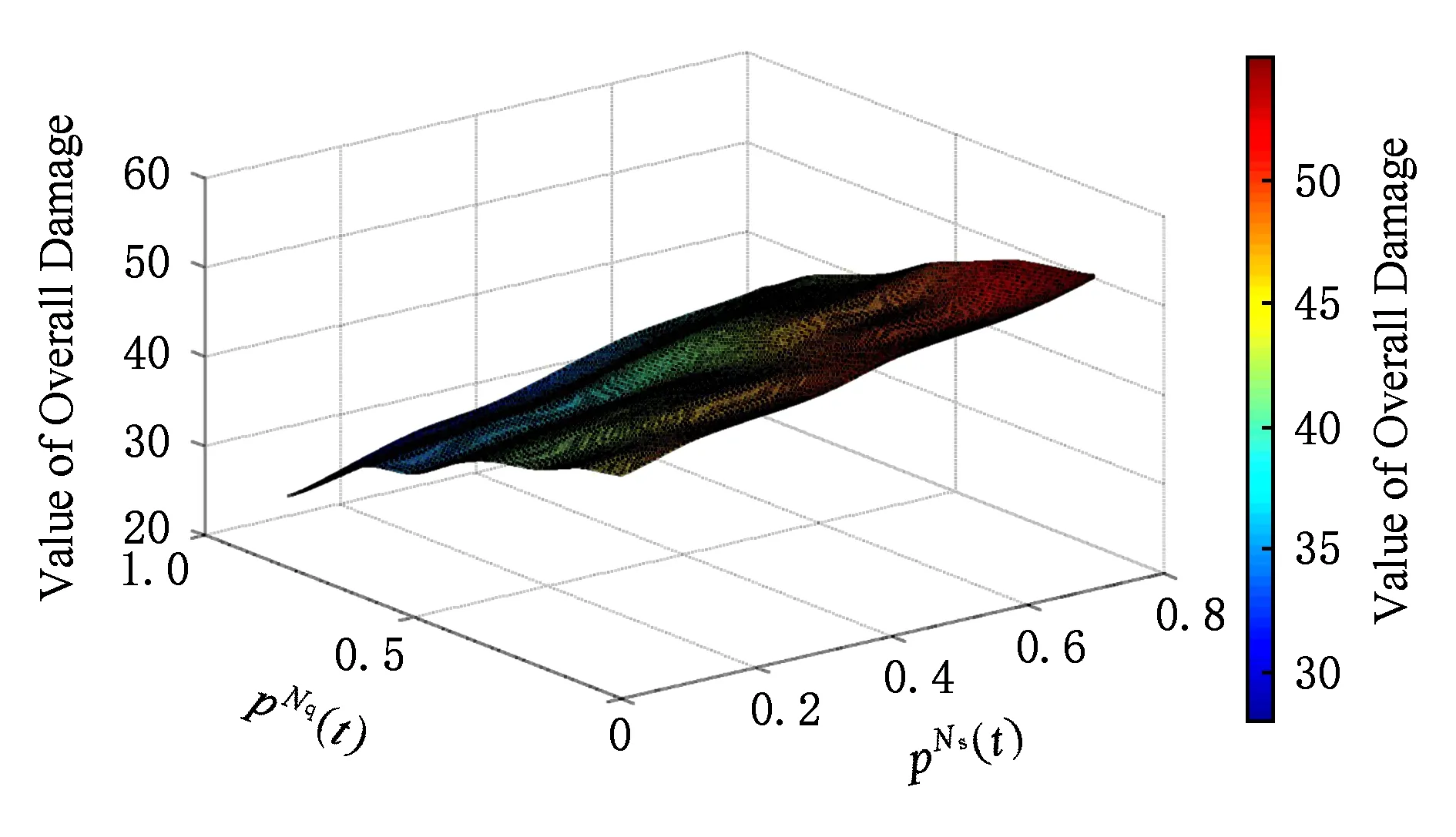
Fig. 11 Target cost under different and 图11 不同和下的目标成本值
由图9~11可知:本文中WSS蠕虫传播最优攻击算法以及最优防御算法的控制参数取值相对于目标成本函数具有最优特性,即图4中的方案在不同博弈阶段的参数取值对攻击者和防御者均为最优策略.基于目标成本值最优的蠕虫传播抑制算法可以最大限度地提高WSS的安全性能.
6 结束语
物联网WSS中的蠕虫传播问题严重限制了其在工业生产、灾害预警、智能管理等领域的应用.为了解决这一问题,自主研究具有最优特性的WSS蠕虫传播抑制算法.
本文提出了一种基于目标成本值最优的WSS蠕虫传播抑制算法,和其他同类型算法相比具有3个方面优点:
1)在传统SIR模型的基础上,引入休眠状态和隔离状态,建立了状态转换图和改进的流行病模型,并给出了各状态节点的微分方程及初始状态,使不同博弈阶段状态节点数量的计算更加准确;
2)本文构建了蠕虫传播的系统模型,利用节点的通信半径以及感染节点的分布规律,准确计算了具有蠕虫传播能力的感染节点数量,使感染节点的状态微分方程对下一时刻状态节点的预测更加精确;
3)本文建立了WSS和蠕虫的动态微分博弈模型,以目标成本值最优作为鞍点策略的求解条件,通过状态变量、协状态变量以及汉密尔顿函数的线性特点实现均衡策略的求解,在此基础上,提出了蠕虫传播抑制最优策略算法,与其他算法相比,本文算法在不同博弈阶段状态节点预测以及WSS蠕虫传播抑制方面具有明显优势.

