城市湖泊景观水体形态定量研究

袁旸洋 朱辰昊 成玉宁

城市湖泊对于景园环境的品质有着重要的影响，也是设计师关注的焦点。湖泊的水体形态在景观空间格局形成中发挥了主要作用。以往对于湖泊景观水体形态的研究多囿于定性描述，本文引入了定量方法对城市湖泊的水体形态展开研究，旨在探讨湖泊景观水体的“形态”特征与规律，以期引导城市湖泊的水体形态设计。

1 城市湖泊的水体形态

形态作为表征事物特征的一种有效方式在多个学科中均有广泛研究。游人在景园环境中对景物感知与体验的形成主要依赖于视觉信息的获取，因此水体形态是最易被游人感知的湖泊景观特征。孟兆祯先生在《园衍》一书中对水景观形态进行了评述：“水的形态外观是水景的基础。大海、湖泊虽难窥其全貌，触目之处亦有水的形态问题。对于城市园林中体量不是很大的水体而言，水形态的景观影响就更大了。”[1]水体形态不仅是城市湖泊景观空间生成的基础，而且曲折变化的水体岸线能够生成丰富多样的近水与亲水空间，为景观的塑造提供更多可能。

1.1 水体形态的定性描述

水本无形，因器成之。湖泊依附于地形生成，其水体形态与“池盆洼地”的形状有着直接关联，多呈现有机、自然的形态。与规则的人工水体不同，自然式水体形态的描述有一定难度，以往常采用比喻、形容等方式。《作庭记》“汀形诸样”篇中就特定的汀形①有如下论述：“池、河水际处之白滨, 其形尖如锄锋，凹似锹形”[2]。以锄头之锋来描述形尖，以“锹形”表达洲滨凹凸变化的水际线形。无论是比喻，抑或是形容，对水体岸线形态的描述均属定性层面，较为模糊与抽象。定性的描述强调直觉、感悟与体会，对于设计而言，抽象的描述难以精确地表征水体的形态，不易掌握与控制。

1.2 水体形态的定量表征

湖泊景观的水体形态研究涉及自由形态的比较与分析。与定性的描述相比，定量的表述强调“规律”的表征。对形态的定量分析与研究有助于寻求其生成逻辑与内在规律。湖泊景观的定量化研究不仅从科学的角度准确地表述岸线的形态特征，而且能够探求“形态”的特征与规律，引导湖泊景观的水体形态设计。

湖泊的水体形状是由岸线围成的几何图形。在湖泊学研究中，湖泊形态度量（lake morphometry）指用数值来表征湖泊平面与立体的几何形状，包括湖泊长度、最大宽度与平均宽度、长轴长度与方向、短轴长度、湖岸线长度、湖岸发育率（湖岸线发展系数）、湖泊面积、岛屿率、湖水面积、湖泊最大深度与平均深度、湖泊容积、湖泊流域面积等几何指标[3]。水体形态的几何指标能够从卫星图、地理数据中直接或间接获得，也易于转化为设计的控制要素，并图形化表达。因此，本文采用了一系列定量化的几何指标对湖泊景观的水体形态进行表述。

2 城市湖泊水体形态定量研究方法

2.1 城市湖泊水体形态定量评价的技术路径

本研究目的为基于定量评价与分析城市湖泊景观案例，探讨水体“形态”的特征与规律。技术路径由“评价指标及案例筛选”“水体形态数据获得”“水体形态数据分析”3部分构成。首先，根据城市湖泊景观的特点确定水体形态的定量化评价指标，筛选评价案例，并选择适宜的卫星影像源；其次，运用ArcGIS、AutoCAD、Grasshopper等软件对卫星影像进行拼合、校正、提取和计算，得到城市湖泊案例的水体形态指标数据集；再次，运用SPSS19.0软件对水体形态指标数据进行分布、相关性和回归分析，得出案例的相关量化指标值，如指标区间值等，并根据结果分析指标间的关系，对城市湖泊水体“形态”的特征与规律进行分析与讨论（图1）。

2.2 基于Grasshopper软件的水体形态指标计算方法

湖泊景观的水体形态有机且富有变化，多为不规则的自然形态，在量化求算时具有以下难点：1）不规则形态的最长轴和最小外接圆面积等数据计算有一定难度；2）由于不同类型指标的计算方法不同，需要依托多个软件平台，数据难以衔接；3）部分数据的计算及汇总等工作需依靠人工完成，工作量大且易产生错误。为了解决以上难点，本研究依托Rhino环境下运行的Grasshopper软件进行运算集编制和数据计算（图2）。一方面，Grasshopper可以准确地对多类型数据进行运算和输出，既能够使数据有效衔接，又避免了人工计算和汇总过程中的误差；另一方面，通过算法编写Grasshopper运算集，实现了数据的精准与高效计算。此外，借助Rhino软件，Grasshopper的运算结果可实时呈现与反馈，便于调控与优化。

3 湖泊景观岸线形态的评价

3.1 评价指标的选择

自然物形态可分为2类，一类具有整数的维数，可以用传统欧式几何学描述；而另一类如海江河湖的岸线、山脉等，因其不规则性和自相似性，不一定是整数维，而是分数维。较之岸线发育系数、近圆率、形状率②、紧凑度等欧式几何形态指标，分形理论为描述复杂的湖岸形态变化提供了更有效的工具。国内外已有学者将分形理论运用于湖泊生态与形态研究，用分形维数揭示湖泊及水系的水文特征[4-5]。本文将分形理论引入水体形态的研究中，将其作为一项定量化指标来表征岸线的复杂程度。

本文用基本几何形态指标、分形几何形态指标与欧式几何形态指标共同表述城市湖泊水体形态，如表1所示。其中，基本几何形态指标中水体面积（A）、周长（P）通过测量可直接得到，最长轴（L）需要计算得出。分形几何形态指标对应的分形维数可描述单个水体岸线的分形特征，即复杂的变化情况。由于湖泊岸线是二维空间的曲线，所以水体形态的分形维数应介于1和2之间，其值越趋近于1，则岸线的自我相似性越强，岸线形状越有规律，岸线的几何形状趋于简单；其值越大，反映岸线的几何形状越复杂[4,6]。从景观生态学角度而言，较长的水体岸线具有显著的边缘效应。岸线的复杂程度越高不仅具有积极的生态意义，而且就形态而言，岸线越复杂所生成的空间也越丰富。但是过于复杂的岸线形态会使水体形态过于“破碎”，导致美感度下降。欧式几何形态指标由岸线发育系数（DL）、形状率（FR）、近圆率（CR）、紧凑度（C）、水体面积包容面积（∆A）构成。

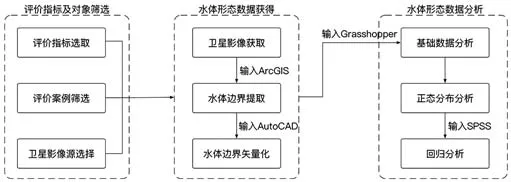
1 城市湖泊景观水体形态定量评价技术路径Technical path for quantitative evaluation technical path of water morphology of urban lake

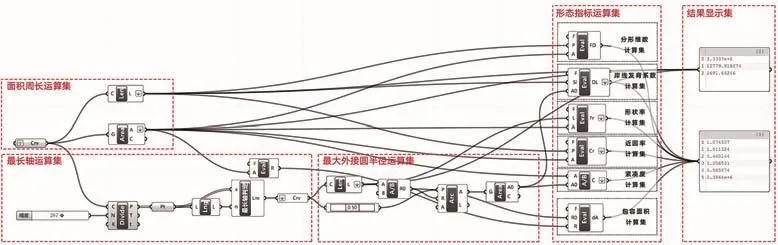
2 Grasshopper运算集Grasshopper operation set

3.2 研究案例的筛选

本文所选案例为东部平原地区城市湖泊[7-8]（表2、图3），选择原则如下：1）公众认可度高、风景优美，对人们有一定的吸引力；2）形态自然有机：案例多为天然形成或人工筑坝生成，岸线曲折，呈自然形态，未经过多的人工干预；3）面积尺度合宜：面积过大的水面难以看到边际，也就失去了研究形态的意义。由于湖泊通常被堤岛划分为若干独立水面，为了保持人视角度水域的完整性以及保证水体岸线的闭合，本文按照堤岛划分的独立水面对湖泊进行分区。本研究所选案例为城市湖泊，水域面积或水体分区面积为1～10km2，水体岸线视线可及，大部分区域可通视。

3.3 基础数据的获得

案例的水体形态基础数据来源于卫星影像图，利用卫星地图抓取器进行高精度的抓取、拼合与修正③，得到精度为1.19m/像素的卫星影像，采用ArcGIS软件提取案例卫星影像中水体边界，将水体形态矢量化，根据堤岛划分的独立水面对湖泊进行分区，例如苏州石湖分为A、B、C、D 4个水岸线的完整水面（图4）。

3.4 评价数据计算

将湖泊景观水体形态基础数据输入Grasshopper软件中编写的运算集，可得到28个案例的3类几何形态指标、9个量化指标共64组数据。

3.5 数据分析与讨论

3.5.1 水体形态指标基础数据分析

将计算所得28个案例的64组水体形态数据样本输入SPSS19.0进行数据的描述统计与正态分布分析，可得到图5和表3。

由图可见，各指标频率均呈偏态分布，且具有明显的集中趋势。表3中案例的水体形态指标如下：最长轴的区间为[621.53，9671.84]；分形维数区间为[1.00，1.17]；岸线发育系数区间为[2.28，9.15]；形状率的区间为[0.08， 0.52]；近圆率的区间为[0.04，0.76]；紧凑度的区间为[0.10，0.67]。结合频率分布图和数据统计表可得到以下结论：

1）由水景形态最长轴分布图，可知87%的数据样本位于[0～4km],其中65%的数据样本位于[0～2km]。所选案例在通视的情况下均位于人眼可视范围以内。

2）由分形维数的频率分布图，可知93%的数据样本位于[1.03，1.15]。与典型天然湖泊（D=1.04）和典型人工湖泊（D=1.21）[12]进行比较研究可知，美景度高的城市湖泊岸线分形维数介于典型人工湖泊水景和天然湖泊水景之间，更偏向于天然水景。所以湖泊类水景的设计可通过水体形态分形维数的调控，避免岸线过于平直而水景形态趋向人工化，丧失美观性与自然趣味。

表1 城市湖泊水体形态定量评价指标Tab. 1 Quantitative evaluation index of urban lake water morphology

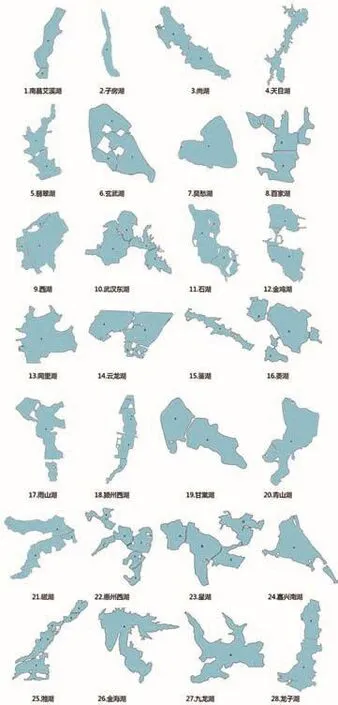
3 28个城市湖泊水体形态平面简图Graphic diagrams of 28 urban lake water morphology

表2 城市湖泊水体形态研究案例Tab. 2 Case study of urban lake water morphology

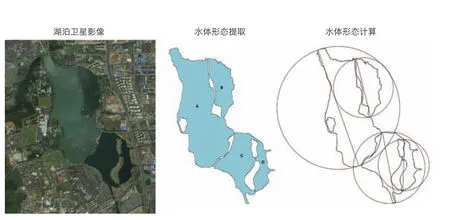
4 基础数据获取过程——以苏州石湖为例Basic data acquisition process—Taking Suzhou Shihu Lake as an example

5 研究案例水体形态指标值频率分布图Histogram of water form index value of case study

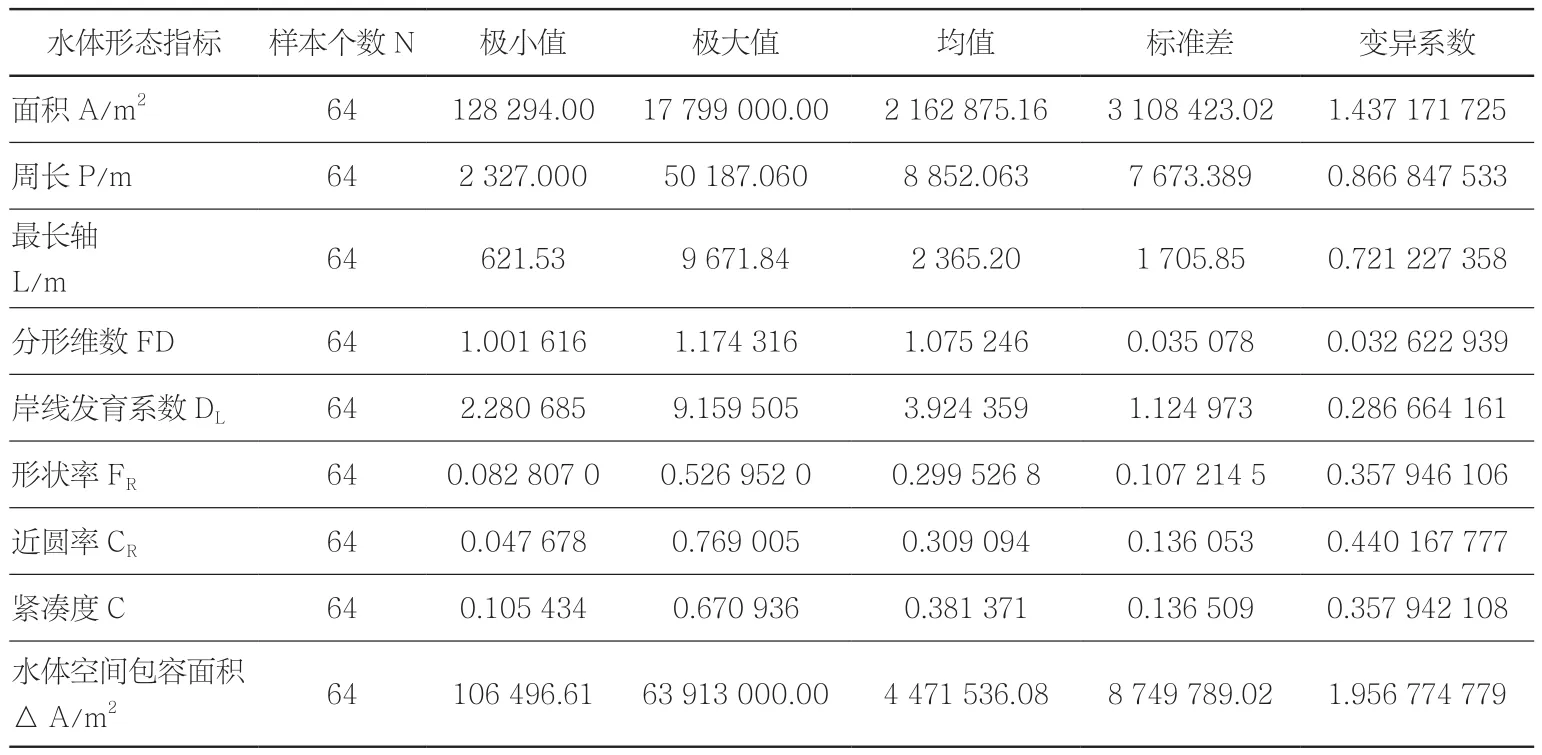
表3 研究案例水体形态指标统计Tab. 3 Statistic of water morphology index of case study

3）由岸线发育指数的频率分布图，可知90%的湖泊岸线发育系数集中在[2，6]之间，72%的湖泊的岸线发育系数小于4。以上数据表明，优美的湖泊景观以流畅、连续的岸线形态为主，呈不规则形状，且具有一定的曲折变化。

4）由形状率和近圆率的频率分布图，可知95%的湖泊岸线形状率≤0.5以及70%的湖泊岸线近圆率≤0.4，说明优美的水体形态整体曲率较大，宽窄变化较多，变化丰富。其中，云台山子房湖与绍兴鉴湖的形状率仅为0.082 807与0.083 067，水体形态表现为水面较一般湖泊景观狭长，岸线曲率大。南昌艾溪湖B水域的近圆率0.769 005，表明此段水域受人工影响较大，岸线较为平直。

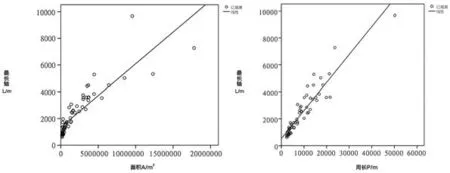
6 最长轴与面积、周长的回归分析图Regression analysis of the longest axis, area and perimeter

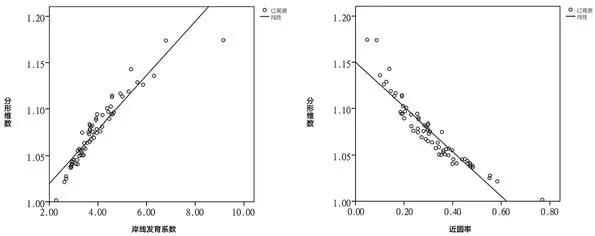
7 分形维数与岸线发育系数、近圆率的回归分析图Regression analysis of fractal dimension, shoreline development coefficient and near-circle ratio

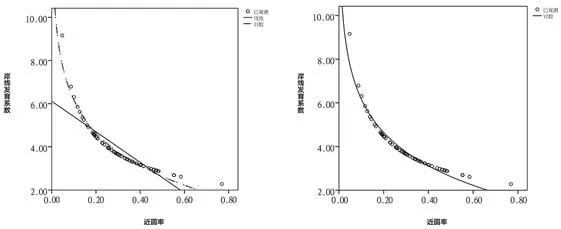
8 岸线发育系数与近圆率的回归分析图Regression analysis of shoreline development coefficient and near-circle ratio

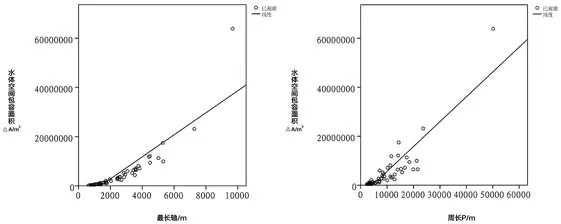
9 水体包容面积与最长轴、周长的回归分析图Regression analysis of water body containment area, longest axis and perimeter

5）由紧凑度的频率分布图，可知紧凑度小于0.5的数据约占总体数据的75%，其中，40%的湖泊岸线紧凑度集中在[0.3，0.5]区间内。由于所选案例大多为于建成环境，湖泊景观的空间格局较为紧凑，但仍具有一定的开阔度，保持有较好的视觉中心。

3.5.2 岸线形态指标数据回归分析

利用SPSS19.0软件对数据进行曲线估计分析，得到各指标间的数据关系。其中，最长轴与面积、最长轴与周长指标、分形维数与岸线发育系数、分形维数与近圆率、近圆率与岸线发育系数、水体包容面积与最长轴、水体包容面积与周长的模型拟合优度指标均大于0.7，说明拟合较为理想，指标间存在密切关系。在此基础上对指标数据进行回归方程求算和分析，进一步研究水体形态指标的相互关系。

1）最长轴与面积、周长。

图6反映了城市湖泊的最长轴（L）和湖泊面积（A）、最长轴（L）和湖泊周长（P）之间的关系，其对应的回归方程分别为：L=0.004A+1337.1（R2=0.750）、L= 0.208A+526.263（R2=0.873）。由图可知，随着湖泊面积和周长的增加，湖泊长轴与湖泊面积和周长成正相关。其中，周长对湖泊最长轴的影响较之面积更为明显。因此，在水景设计时通过增加岸线曲折度等方式增加湖泊周长可对最长轴产生影响，从而增加湖泊景观的景深。

2）分形维数与岸线发育系数、近圆率。

图7反映了分形维数（FD）和岸线发育系数（DL）、分形维数（FD）和近圆率（CR）之间的关系，其对应的回归方程如下：FD=0.29DL+0.961（R2=0.879，P＜0.001）、FD=–0.241CR+1.15（R2=0.875，P＜0.001）。可见随着岸线发育系数的增加，分形维数会相应增加，说明通过增加水岸的曲折度可提升水景整体丰富度与自然性。由此，在设计实践中亦可通过增加局部岸线的曲折程度以增强湖泊景观的丰富度，并模拟自然岸线形态。而分形维数与近圆率则呈反相关，随着近圆率的增加，分形维数值呈现减少趋势。因此在设计实践中需注意湖泊水体形态的空间变化，宜收放有度，避免水体形态过于狭长。

3）岸线发育系数与近圆率。

由岸线发育系数（DL）和近圆率（CR）线性回归分析可发现数据呈现明显的对数分布（图8）。因此使用对数模型重新拟合模型，得到回归方程如下：DL=CR–2.205+1.098（R2=0.957）。由分析可知，随着近圆率的增加，岸线发育系数会显著减少，但其减少速率会逐步放缓。在设计实践中需考虑近圆率对岸线发育系数的影响，趋于圆形会使水体岸线均质化，既丧失了空间的趣味，也弱化了岸线的生态功能。

4）水体包容面积与最长轴、周长。

图9反映了水体包容面积（△A）与最长轴（L）、周长（P）之间的关系，其对应的回归方程如下：△A= 4 478.29L–6 120 514.612（R2=0.762）、△A= 4 478.29L–6 120 514.612（R2=0.792）。水体包容面积随着最长轴和周长的增加，呈现增加的趋势，并且周长的变化对水体包容面积的影响较大。在设计中可以根据实际要求，通过调节水体形态的最长轴和周长对水体的空间包容面积加以调控，增强水面空间结构变化而引起的陆面扩大效应，提高湖泊景观效益。

表4 城市湖泊形态特征定性与定量指标Tab. 4 Qualitative and quantitative indicators of urban lake morphological characteristics

4 结论与展望

本研究采用了面积、周长、最长轴、分形维数、岸线发育系数、近圆率、形状率、紧凑度、水体空间包容面积9个、3类几何定量指标对平原湖泊景观的岸线形态进行描述，并选取了28个城市湖泊为案例进行量化研究，利用Grasshopper软件构建水体形态运算集进行数据计算，得到了城市湖泊水体形态的定量指标值区间。经过分析可知，最长轴与面积、最长轴与周长指标、分形维数与岸线发育系数、分形维数与近圆率、近圆率与岸线发育系数、水体包容面积与最长轴、水体包容面积与周长之间均存在紧密关联。

通过28个城市湖泊案例分析所得指标值区间定量化表述了湖泊水体形态特征，对城市湖泊景观的设计具有一定普适性参考意义。在设计实践中可将城市湖泊的景深、岸线丰富度、岸线曲折度、岸线自然度、水面开阔度等定性指标与定量指标相关联，根据本文研究所得定量指标值区间对城市湖泊的“形态”进行评价，从而为湖泊景观的设计与优化提供引导（表5）。

此外，通过回归分析，本文探讨了最长轴指标与面积、周长指标，分形维数与岸线发育系数、近圆率与岸线发育系数，以及水体包容面积与最长轴、周长的相互关系，解析归纳了城市湖泊景观平面“形态”的特点与规律。城市湖泊形态定量指标间的关联能够转化为水体形态的参数化逻辑关联，同时可根据定量指标间的回归方程编写相应算法，用于调控水体形态，有助于实现拟自然水景的参数化生成设计[13-16]。

城市湖泊景观具有复杂性，其空间生成受多种因素的影响。本文的研究聚焦于湖泊形态的二维平面，定量化研究为有机、不规则的水体形态提供了一种较为精确与直观的表述途径，便于设计实践中的运用。本文所选指标，如近圆率、形状率、紧凑度、岸线发育系数、分形维数等为水生态研究中常用几何指标，在日后的研究中可引入连接度（Connectance Index）、蔓延度（Contagion Index）、回旋半径（Radius of Gyation）等景观生态学指标，结合“生态”与“形态”进一步定量化探讨城市湖泊景观“美”的特征与规律。

注释：

①“汀形”指与水相交所成之水际线形。

②“近圆率、形状率”为地理学应用研究中的形状指标，用于简要叙述在三维状况下的空间形状特征。详见参考文献[9]。

③ 卫星影像来源：ArcGIS Earth；分辨率：1.19m/像素；时间：2010年。

④ 文中图表为作者自绘。