考虑电势非线性分布的电渗固结理论

储 旭

（上海市政工程设计研究总院（集团）有限公司，上海市 200092）

0 引言

电渗法或与真空预压、堆载预压等的联合工法是目前处理软基最有效的方法之一。Casagrande于1939年第一次将电渗技术应用于岩土工程中，提出了电力渗流的概念[1]，此后，该方法应用于不同类型的软土加固中。1968年，Esrig提出了一维电渗固结理论，用于解释电渗过程中孔隙水压力的增长与消散现象[2]。Wan和Mitchell于1976年在Esrig理论的基础上提出电渗联合堆载预压的一维固结理论[3]。Shang将其扩展到二维空间，计算分析了某一电渗工程实例，取得了不错的效果[4]。在他们的电渗固结理论中，均假定电渗土体中电势分布为线性分布，但此假定与实际是有明显的偏差的[5,6]。庄艳峰等[7]根据导电面积的大小，突破土体电势线性分布的局限，提出了电渗界面电阻理论，但未能与电渗固结理论相结合。苏金强等[8]根据试验结果拟合出一个电势分布的经验公式，给出了不同边界条件下的二维电渗固结的理论解。但由于拟合的经验公式不具有普遍性，使得其适用范围受到限制，且某些计算结果的准确度较低。

由于电渗本身属于一种电学现象，在不考虑电化学作用的土体中不存在自由电荷，其电势分布符合拉普拉斯分布，故本文采用电势的拉普拉斯分布，对现有的电渗固结理论进行重新求解。通过一个电渗模型箱算例及文献中的一个室内电渗模型实验的数值计算，以验证采用电势拉普拉斯分布的合理性。

1 电渗固结理论

1.1 基本假定

（1）土体均匀饱和，正交各向同性，土粒与水的压缩忽略不计，土的压缩完全由孔隙体积的减小引起；

（2）土体的水力渗透系数和电渗透系数不随时间而改变；

（3）不考虑土体中各种浓度和热差而引起水流，不考虑电化学反应；

（4）电渗电极和土体接触良好，之间没有电压损耗；

（5）由电势差和水头差引起的水流可以叠加；（6）土体中电势分布不随时间变化。

1.2 电势分布方程

根据电学原理[9]，当空间电场为流电场时，电流密度为：

式中：I为电流密度；σe为土体的电导；ih为水力梯度，ih=grad（H）=grad（u）/γw；γw为水的容重；σh是由于水流引起的电导，σh=keγw；ke为电渗透系数；ie为电势梯度，ie=grad（φ）；φ 为土体电势。

由于土体中水流流速很低，且 σh≤σe，式（1）中水流流动引起的电流可忽略不计，则：

根据基本假定（6）可得：

1.3 电渗固结方程

电渗过程中，土体中的水流是由水力梯度和电势梯度驱动的耦合流，由基本假定（5）可知：

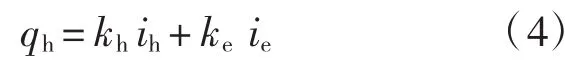
式中：qh为水流；kh为水力渗透系数。由Tazaghi固结理论可知：

式中：mv为土体体积压缩系数。

对于三维固结情况，由电渗耦合流式（4）可得：

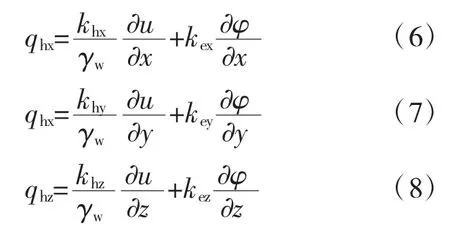
故得：

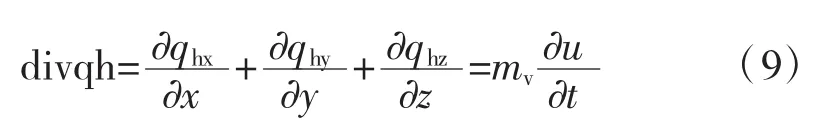
根据基本假定（1），khx=khy=khz=kh，kex=key=kez=ke。将式（6），（7），（8）代入式（9），得

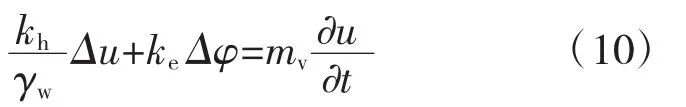
设定一个虚变量ξ

根据假定（6），可将式（10）变换成为：

1.4 定解问题

由电势分布式（3）、电渗固结式（12）联立组成电渗控制方程组

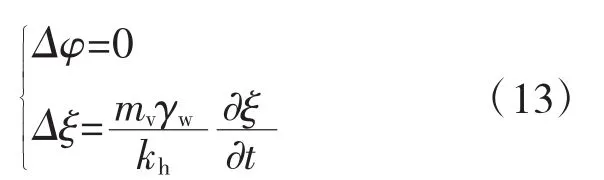
（1）边界条件

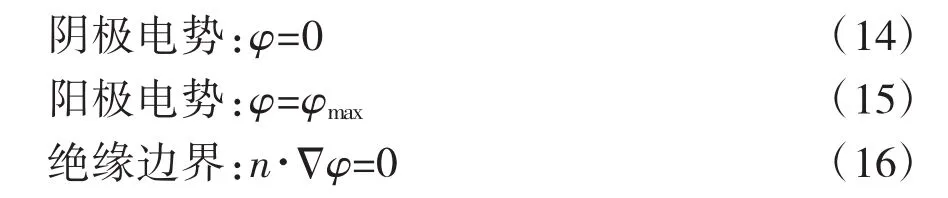
式中：n为边界的外法线方向；为哈密顿算子。

阴极排水：由于u=uc（uc为在阴极处施加的孔压值），φ=0，则

阴极不排水：qh=0，则

阳极排水：由于u=ua（ua为在阳极处施加的孔压值），φ=φmax，则

阳极不排水：qh=0，则

透水边界：u=ub，ub为在透水边界施加的孔压值，φ=φb，φb为边界处的电势，则

不透水边界：

（2）初始条件：u=u0，u0为初始时刻土体中的孔压，则

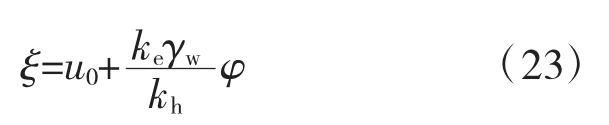
以上式（13）～式（23）构成了一个完备的定解问题。

1.5 定解问题的解

土体中任意一点t时刻的孔压ut：

式中：ξt表示t时刻的虚变量ξ值。

排水边界为Ω，t时刻的土体排水率D为：

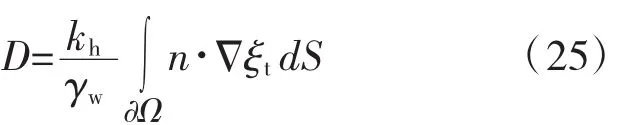
沿高度H方向t时刻的沉降S：

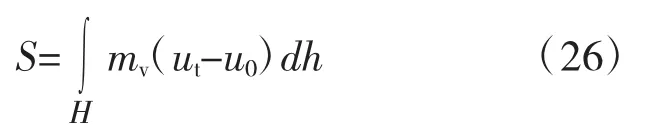
电渗过程中，在总应力不变的情况下，饱和土体有效应力的增加等于孔隙水压力的消散。因此，t时刻土体的含水率ωt为：

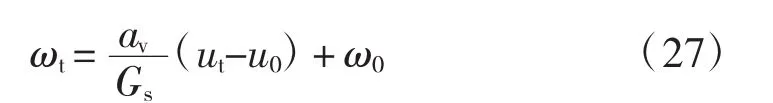
式中：av为压缩系数；Gs为土粒比重；ω0为土体初始含水率。

2 算例分析

由于电渗几何边界条件的复杂性，以上定界问题的解析解不易求出，本文采用数值计算的方法对一电渗模型箱试验进行了求解。模型箱长80 cm、宽40 cm，阴极和阳极的直径为2 cm，阴阳极间距60 cm，其俯视图见图1。

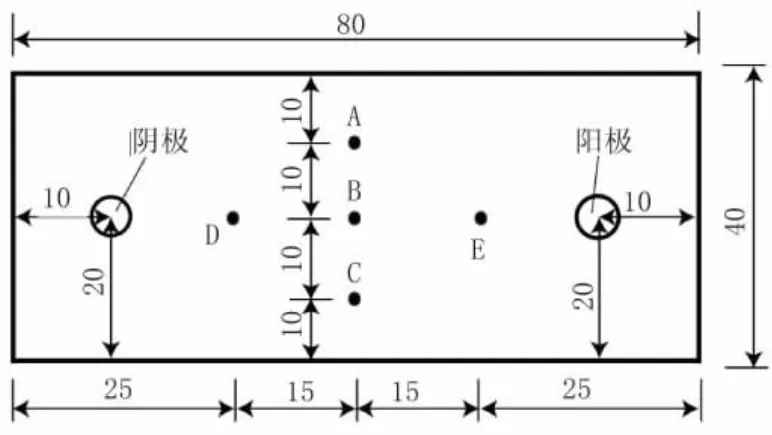
图1 电渗模型箱俯视图（单位：cm）

选取某港口工程中饱和黏土的计算参数：ke=2×10-10m2/（s·V）；kh=4.6×10-10m/s；Gs=2.75；av=1.13 MPa-1；mv=0.49 MPa-1；ω=47.4%。

2.1 电势分布

传统的电渗固结理论中，都是假设阴阳极之间的电势分布为线性分布，并且只能计算阴阳极之间的点，如图1中的D、B、E点，宽度方向其他的点如A、C点则不能进行计算。引入电势的拉普拉斯分布，则能计算出各个点的电势。在阴阳极之间施加4 V的总电势，计算出的土体电势分布见图2，这与Shang等的结果相近[10]。

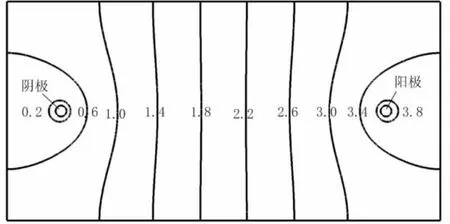
图2 土体电势分布图

图3为分别采用非线性方法和线性方法计算出的阴阳极之间的电势。从图中可以看出，由非线性方法计算出来的电势在电极附近下降很明显，中间部分比较符合直线分布，总体偏向折线分布。这与很多文献中的电渗试验测得的结果一致[4,11]。

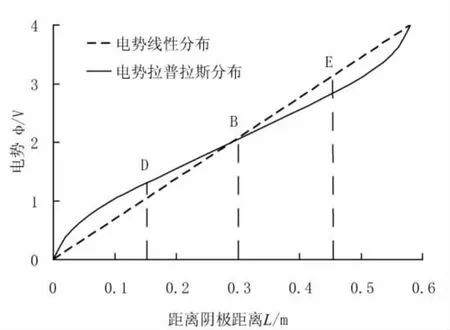
图3 阴阳极之间的电势线性分布和非线性分布图

2.2 孔压计算

在阴阳极之间施加4 V电压，阴极自由排水，阳极和边界不排水，初始孔压为0 Pa，计算时间为12×106s（约140 d），计算土体产生的孔压。

由Esrig的电渗固结理论可知，电渗平衡时土体中的孔压分布与电势分布一致，电势大小决定孔压大小，电势梯度的大小决定了孔压的收敛速度。图4为分别采用电势非线性和线性分布计算出的典型点孔压的增长过程。与图3结合起来看，B点位于电极中点，采用电势非线性分布和线性分布计算出的电势大小相同，但采用非线性分布计算出的电势梯度要小于线性分布的计算值。因此，图4（a）中采用电势非线性分布计算出的B点孔压增长速度低于线性分布计算值，后期两者逐渐接近；D点采用电势非线性分布计算出的电势大于线性分布的计算值，电势梯度小于线性分布计算值。图4（b）中，电势非线性分布计算出的D点孔压值初始时小于线性分布计算值，然后逐渐超出；E点采用非线性分布计算出的电势和电势梯度均小于线性分布计算值。图4（c）中，电势非线性分布计算出的E点孔压值一直小于线性分布计算值，收敛速度也低于线性分布计算值。

同时，在电极连线之外的A、C点则只能采用非线性分布进行计算，两点的电势和电势梯度大小与B点相差不大，所以孔压值也比较接近。当t=1.2×106s时孔压变化很小，电渗固结基本完成。

2.3 排水率计算

在本计算模型中，阴极自由排水，阳极和边界不排水。图5为电渗过程中土体的排水率。可见，在整个计算时间内，土体排水率的大小逐渐衰退，当电渗稳定时排水率衰减至0，符合一般规律。

3 实例分析

Guy和Fabien在2002年做了一个室内电渗固结试验[12,13]，试验数据完整，被很多文献引用。下面利用本文改进的电渗固结理论对该试验进行分析。

Guy共进行了5组实验，与本文研究内容相似的为编号27ET的模型试验，选取其作为实例进行分析。试验土样为加拿大魁北克省圣劳伦斯低地的原状土。计算所需的土样基本参数为：ke=2.7×10-9m2/（s·V）、kh=3×10-10m/s、av=1.5 MPa-1、mv=0.54 MPa-1、ω=49%、Gs=2.79，均直接引自原文。

电渗试验在一PVC材料制作而成的圆筒内进行，圆筒直径为25.4 cm，高为13 cm，见图6。试样顶面、底面各设置一层土工织物作为排水层。电极为 2根阴极（C1，C2），2根阳极（A1，A2），直径1 cm。阴阳极并排布置，同极之间间距10 cm，阴阳极之间间距15 cm。阴极处的水由泵抽出，使液面保持在土体上表面以下2 cm处。土样阳极附近注入某种盐溶液，用以增加阳极附近土体的导电性，尤其是后期的导电性。

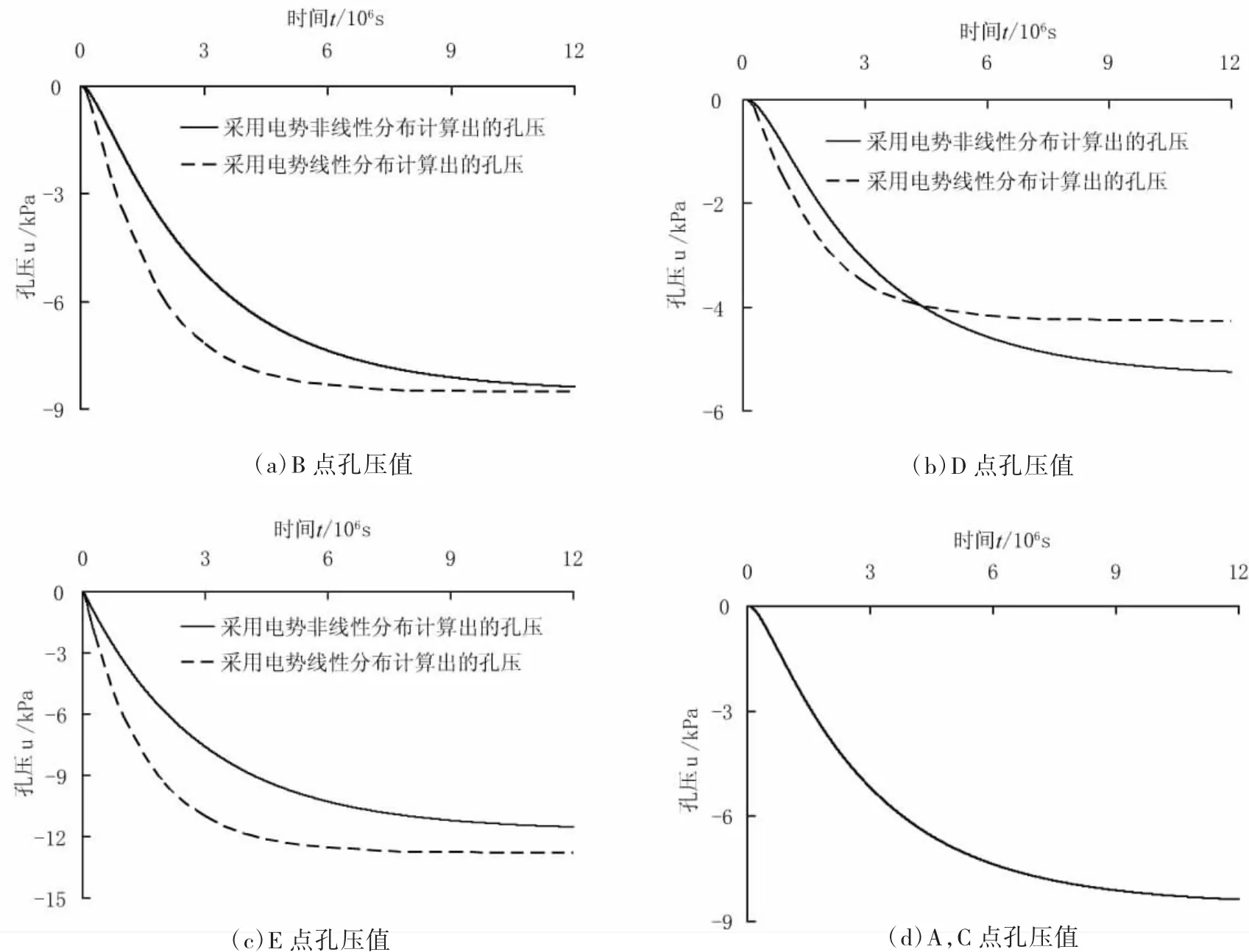
图4 采用电势非线性和线性分布计算出的孔压值

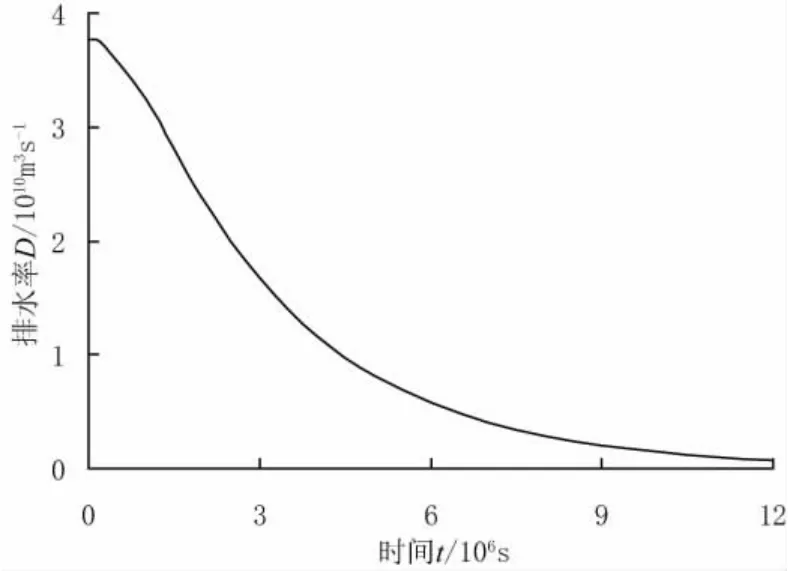
图5 电渗排水率

电渗试验分为两个阶段。第一阶段，土体在175 kPa的上部荷载作用下固结一段时间，水通过上下两面的土工织物排出。固结后测得试样高度10.0 cm，有效应力为170 kPa，故得出电渗时的土体初始孔隙水压力为5 kPa。第二阶段，上部荷载保持为175 kPa不变，阴阳极之间施加总电压5.25 V，电渗6 d。由于该试验几何边界的复杂性，只考虑电势线性分布的电渗固结理论无法进行精确计算，更无法计算出土体排水率，而采用本文中所给出的考虑电势拉普拉斯非线性分布的电渗理论则可以进行计算。表1为电渗固结后试样高度与含水率的实测值和计算值，两者很接近，误差不超过3%。原文中给出的电渗固结后的高度通过位移计测量而得，含水率为平均含水率。

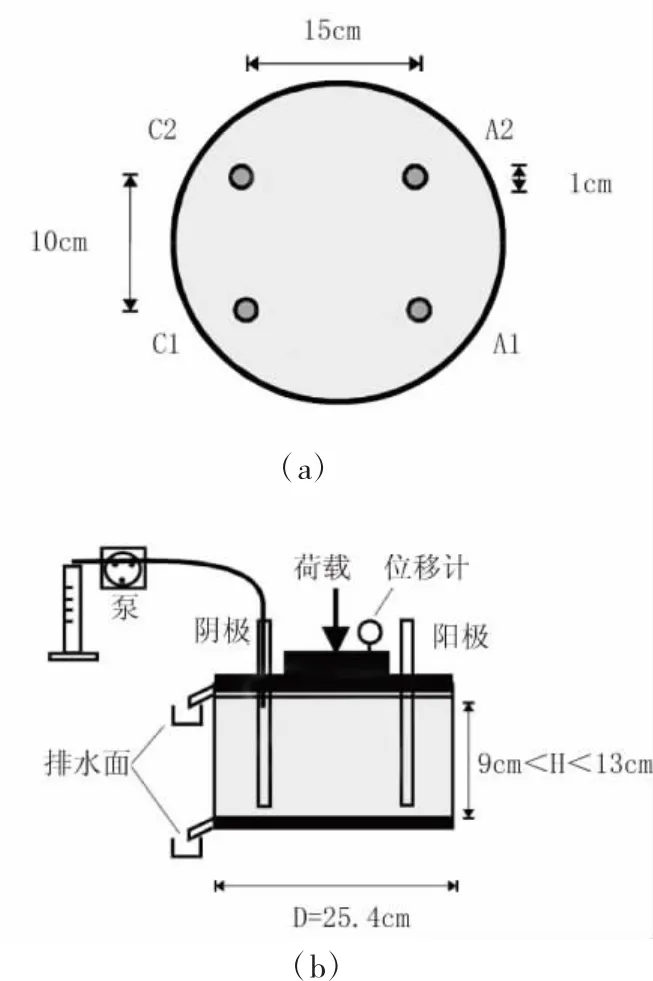
图6 电渗模型箱俯视图（a）和正视图（b）

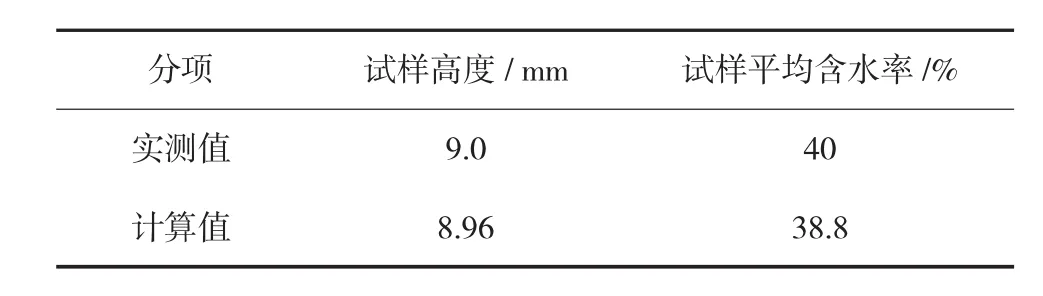
表1 电渗固结后试样高度与含水率的实测值与计算值

Guy在原文中给出了电渗相对排水量随时间的变化。电渗相对排水量为电渗排水量与土体总体积的比值。图7给出了计算值和实测值的对比，从中可以看出总体相差不大。

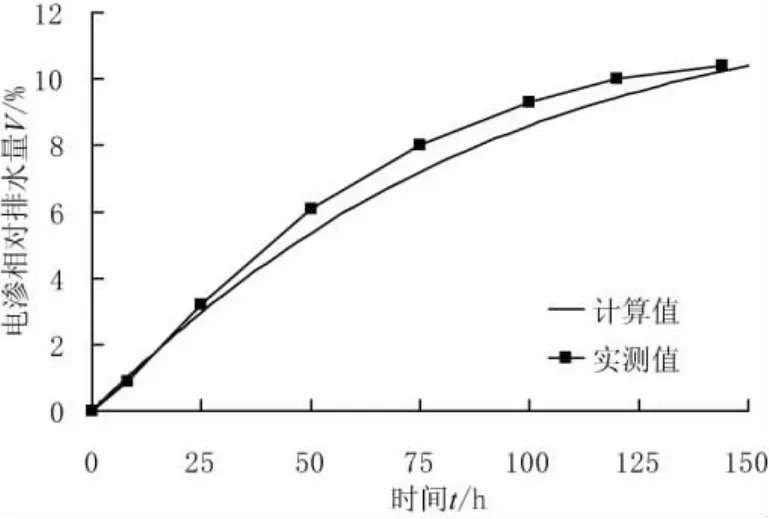
图7 电渗相对排水量计算值和实测值

这个实例分析表明考虑电势非线性分布的电渗固结理论的求解精度高，这主要原因是考虑了电势的非线性分布。此外，实验中的电渗排水量与垂直沉降的体积几乎一样，这表明土体几乎一直处于饱和状态，没有垂直向的裂隙。而且试验过程中的电势比较稳定，因为在阳极注射了某种盐溶液，而实际电渗工程中当施加的电势梯度较大时，电势不可能有这个试验中那样稳定，尤其是电渗后期。

4 讨论

本文的电渗固结理论是基于6点假设建立起来的，而这些假设与实际情况必然有些出入，因此，有必要进行相应的讨论：

（1）电渗固结后期，阳极附近的土体会逐渐由饱和状态变成非饱和状态，并常常伴有裂隙产生，这时候还采用饱和土的电渗固结理论计算显然不符合实际。

（2）电渗过程的本质是土体的电化学反应，但是电渗固结理论中忽略了电化学反应的影响。这在电渗初始和中间阶段还是能接受的，但是到了后期的影响越来越明显，产生离子浓度流，甚至于改变土体电阻率等各种基本性质，这时它对电渗固结的影响很大。

（3）文中假定土体电势分布不随时间改变。在实际问题中，电渗前期和中期电势分布变化不大，后期的电势梯度开始逐渐变化，等势线向阳极靠拢，这与文中假定有一定出入。

由以上讨论可以看出，电渗固结理论在初期和中期还能够进行相应的计算，但是到了后期，土体各种性质的改变限制了电渗固结理论的应用。所以，对于长期的电渗固结计算，文中的电渗固结理论不适用。

5 结语

在Esrig电渗固结理论的基础上，本文引入电势的拉普拉斯分布，配合以相应的边界条件，构成了一个完备的定解问题。该固结理论可以计算复杂几何边界的电渗固结土体，预测土体排水量，土中任意点的孔压，沉降和含水率。由于土体性质的改变，该电渗固结理论不适用于长期的电渗固结计算。

致谢：本文在微分方程的推导和计算中得到了南京水利科学研究院傅中志博士的大力帮助，在此表示衷心感谢！