联塔分幅组合梁斜拉桥抗震性能研究

高宝

（(浙江省交通规划设计研究院，浙江 杭州 310006）

1 工程概况

宁波市绕城高速公路是宁波市高速公路规划“一环五射”中的“一环”。其直接连接甬台温复线、同三高速公路、穿山疏港高速公路及舟山大陆连岛工程，是杭州湾南岸高速公路网核心的一部分。甬江特大桥是宁波绕城公路东段项目的控制性工程，对于整个项目的顺利建成具有决定性地位,甬江特大桥[1]按双向八车道高速公路设计，设计速度为120 km/h，设计使用年限100 a，甬江特大桥位于宁波市区东部，连接北仑和镇海，桥位距甬江出海口约10 km。主桥设计为54 m+166 m+468 m+166 m+54 m联塔分幅四索面钢混组合梁斜拉桥方案（见图1），边中跨比采用0.47，主梁为钢混组合梁。

1.1 结构体系

甬江特大桥采用五跨连续半漂浮体系，空间密索型布置。索塔处设置一对竖向支座，纵向中跨侧设置粘滞阻尼器，粘滞阻尼器对脉动风、刹车和地震引起的动荷载具有阻尼耗能作用，而对温度和汽车引起的缓慢位移无约束，横向设置抗风支座，用于抵抗风荷载及地震荷载作用下的主梁横向变位。辅助墩和边墩顶均设置竖向支座一对。辅助墩和边墩顶除设置竖向支座外，横向设置限位挡块[1-3]。

1.2 主梁

主梁采用钢梁与混凝土桥面板叠合梁，二者通过剪力钉相结合。钢梁部分由纵梁、横梁及小纵梁共同组成钢梁格体系，其中：纵梁每12.0 m一个节段（锚跨为9.3 m），每间隔4.0 m设置一道横梁（锚跨为3.1 m），每两道横梁之间设置一道小纵梁。桥面板采用分块预制、现浇湿接缝连接的方式，其中横向分为两块预制板，共三道纵向现浇缝。

1.3 索塔及基础

索塔采用双钻石形联塔形式，由上、下塔柱和横梁、塔座以组成，其中上塔柱为锚索区塔柱，上、下塔柱在横梁处合并为一体（见图2）。桥塔总高度为141.5 m。桥塔顺桥向塔柱宽度由塔顶7.0 m直线变化到塔底10.0 m。横桥向塔顶宽9.0 m，上塔柱除左右幅两塔联结及上部二柱交会处，余均各宽4.0 m。下塔柱横向宽度由4.0 m直线变化至塔底的6.0 m。塔柱采用箱形断面，塔顶为7.0 m×9.0 m双箱形断面，上塔柱单柱为7.0 m×4.0 m～9.437 m×4.0 m单箱形断面，设环向预应力钢束平衡斜拉索在塔壁内产生的混凝土拉应力。

索塔基础采用钻孔灌注桩基础，承台呈矩形，承台厚6 m，顶面高程2.0 m。钻孔灌注桩直径2.2 m，间距5.8 m，桩基按摩擦桩设计。

1.4 辅助墩、过渡墩及基础

辅助墩和过渡墩的形式与索塔及全桥景观协调一致，选择矩形双柱V形墩。实心墩柱截面尺寸为3.0 m×3.0 m～3.0 m×3.5 m。辅助墩与过渡墩采用分离基础，墩身横向分开设置。辅助墩与过渡墩承台、墩身均采用C35混凝土。

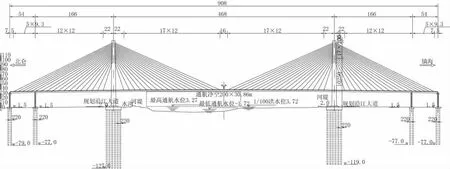
图1 桥型布置（单位：m）

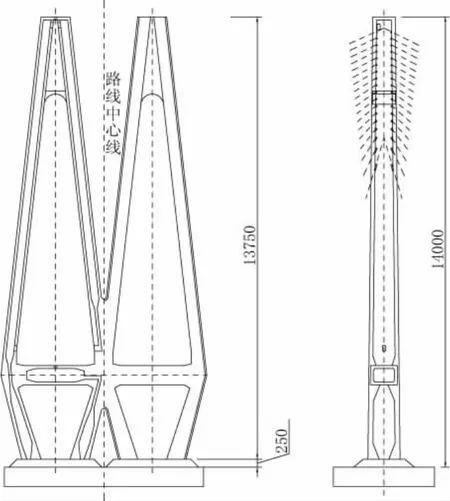
图2 双砖石形桥塔构造（单位：cm）

1.5 场地条件

根据《甬江特大桥设计地震动参数专题研究报告》工程场地基本烈度为Ⅶ度。100 a 10%超越概率的工程场地水平加速度峰值为0.131g，100 a 3%超越概率对应水平加速度峰值为0.153g，竖向加速度取水平向的1/2，选取的场地水平加速时程曲线见图3、图4。

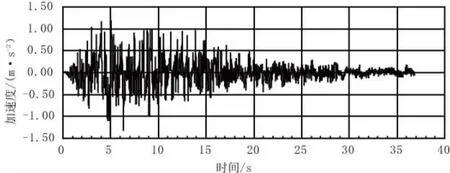
图3 工程场地水平加速度时程曲线（5%阻尼比，100 a超越概率10%）

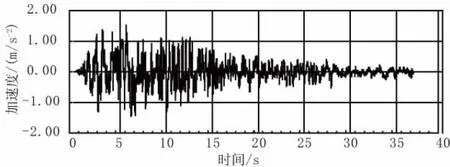
图4 工程场地水平加速度时程曲线（5%阻尼比，100 a超越概率3%）

2 动力计算模型建立及动力特性分析

2.1 动力计算图式

为准确求解该桥的动力特性，需建立空间三维模型，对实际结构进行模拟，尽可能使模型中的刚度、质量及边界条件与实际相符。采用SAP2000 Nonlinear有限元程序，应用三维有限元模型分别建立非线性动力计算模型进行抗震性能分析，把主塔、主梁、横隔梁、桥墩等均离散为空间梁单元，斜拉索用空间桁架单元模拟，并考虑拉索垂度效应以及恒载下初始几何刚度影响，建立”鱼骨式”分析模型（见图5）。边界条件模拟为：主塔及桥墩底采用空间弹性约束，主塔与主梁间采用横桥向主从约束，桥墩与主梁间为竖向及横桥向约束[4-6]。

图5 全桥计算模型

2.2 动力特性分析

斜拉桥的动力特性分析是研究斜拉桥动力行为的基础，其自振特性决定其动力反应的特性，对漂浮体系斜拉桥，纵漂振型常是最低的振型，并对桥梁的纵向地震反应的占主要贡献；一阶竖弯振型对桥梁的地震响应和抗风稳定性有较大的影响；一阶侧弯振型对横行风荷载作用及横向地震反应的影响较大；一阶扭转振型在桥梁的颤振中占主要成分，是影响桥梁空气稳定性的主要因素；因此前几阶振型对斜拉桥结构的抗震性能具有重要意义。由于大跨度斜拉桥柔度比较大，所以振动周期长，固有频率比较低。表1列出了结构的前8自振频率及振型特点，可以看出桥梁的前8阶振动频率都在0.1～0.4 Hz之间，并且模态分布比较密集，结构多会出现耦合振动，如主梁纵漂与竖弯的耦合振动、主梁竖弯和扭转的耦合振动等。

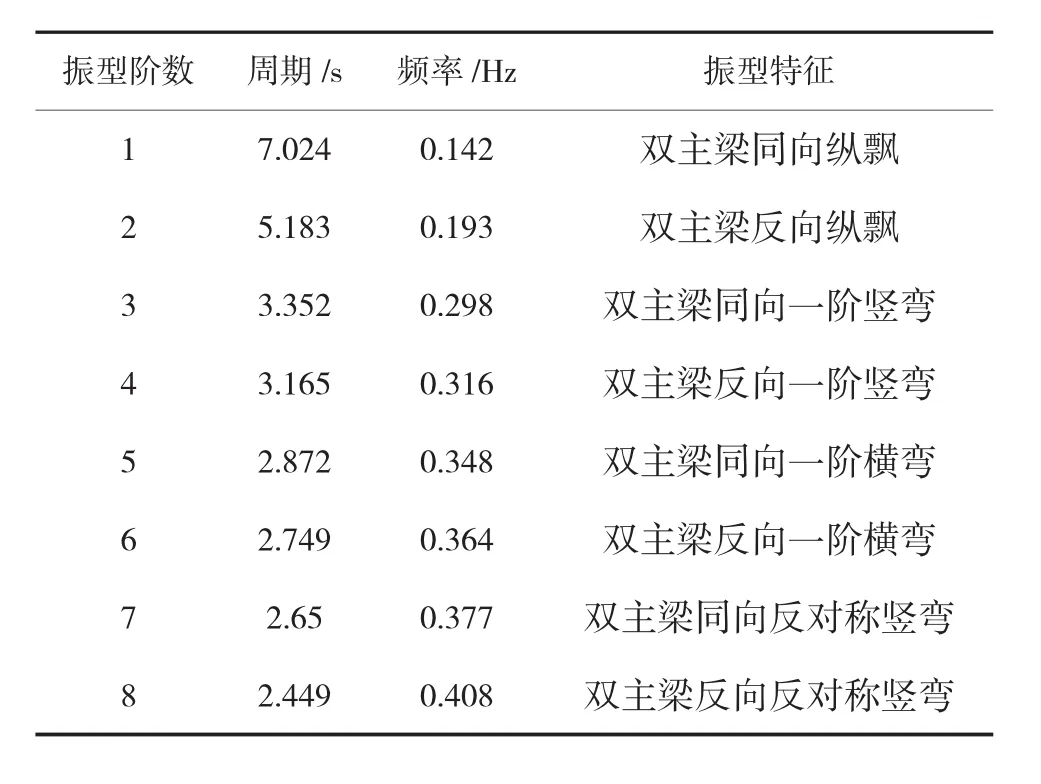
表1 结构自振频率及相应振型对比

3 地震反应分析结果比较

针对非线性有限元模型，分别在100 a 10%（即P1概率）和100 a 3%（即P2概率）两种超越概率下进行时程反应分析，非线性因素考虑两种情况：第一种仅考虑纵向滑动支座摩擦力，其中动摩擦系数取0.02；第二种为同时考虑塔梁纵向粘滞阻尼器和纵向滑动支座摩擦力，其中阻尼器选用参数：阻尼常数C=2 000，阻尼指数ξ=0.2，阻尼器布置为每幅桥塔梁连接处设两个阻尼器，全桥共计8个，其它纵向滑动支座动摩擦系数取0.02。

表2中列出了各工况下的塔顶及跨中主梁的位移反应峰值。可以看出，在纵向地震波输入作用下，索塔和主梁的纵向位移反应比较明显，体现了第一阶纵漂振型对地震反应的贡献比较大。在仅考虑滑动支座摩擦力因素下，P1概率对应的塔顶纵向位移峰值为0.4 m,主梁纵向位移峰值为0.361 m,二者数值比较接近，塔顶位移略大；而在P2概率下塔顶纵向位移峰值增大至0.72 m,主梁纵向位移峰值为0.708 m；塔梁间增设纵向粘滞阻尼器连接后，塔顶及主梁纵向位移均大幅降低，但主梁竖向位移变化不大，说明该粘滞阻尼器具有显著的耗能效果，但具有显著的方向性，即约束纵向变位，对其他方向变位基本无影响。

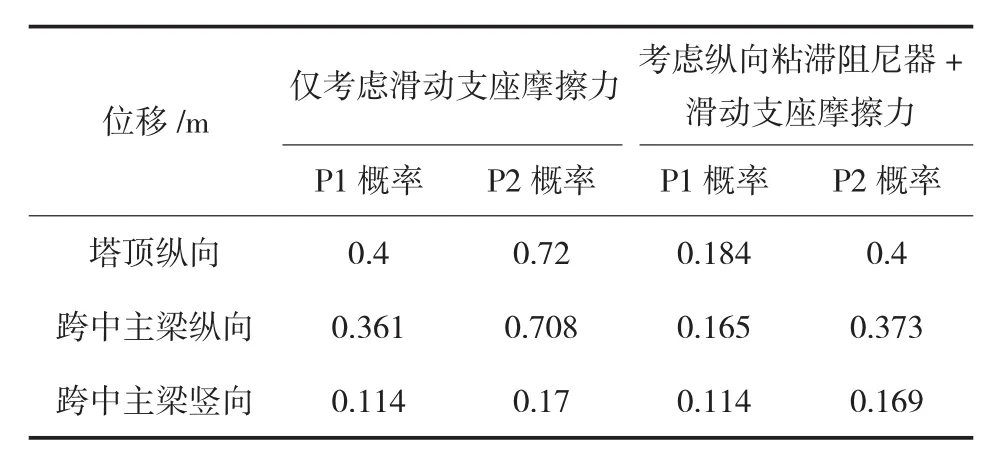
表2 纵向地震波输入下索塔及主梁位移峰值

表3为地震反应下索塔关键截面及辅助墩、过渡墩墩底处的内力结果,从表中可以看出，不同于常规桥塔，联塔分幅斜拉桥桥塔X连接(横梁)处截面也是受力控制截面，主要受双主梁反向纵飘振型产生的惯性力影响。当塔梁间增设纵向粘滞阻尼器连接后，P1概率下的索塔X连接 (横梁)处纵向弯矩由585 747 kN·m降低至310 691 kN·m，塔柱底截面纵向弯矩由601 157 kN·m降低至287 710 kN·m，折减率约50%；P2概率下的主塔X连接(横梁)处纵向弯矩由917 563 kN·m降低至605 954 kN·m，塔柱底截面纵向弯矩由927 727 kN·m降低至552 788 kN·m，折减率约30%；而两种概率水准下，辅助墩、过渡墩墩底纵向弯矩虽有所降低，但变化较小，可以推断出塔梁间的纵向粘滞阻尼对远端的辅助墩及过渡墩影响较小。

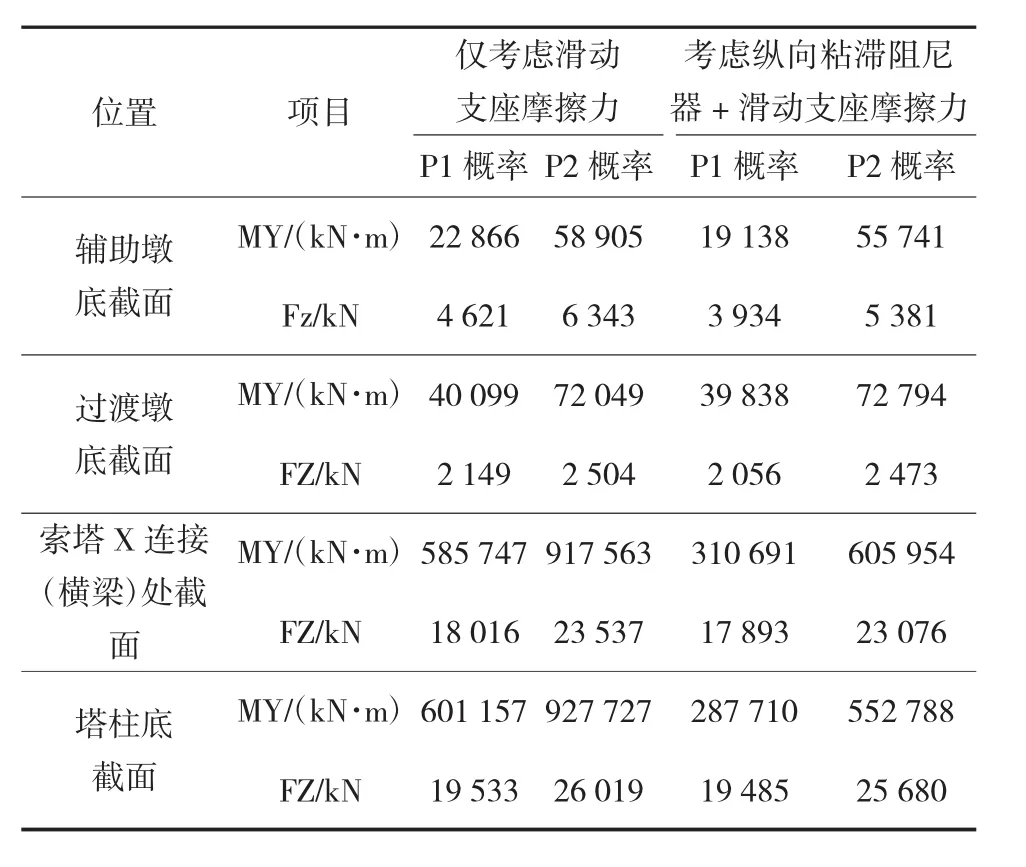
表3 索塔及辅助墩、过渡墩控制截面的内力组合

表4为索塔及辅助墩及过渡墩桩基的最不利内力结果，从表中可以看出，塔梁间增设纵向粘滞阻尼器连接后，索塔基础单桩最不利内力显著降低，而辅助墩及过渡墩基础变化不大，所反映出的规律与表3相似。

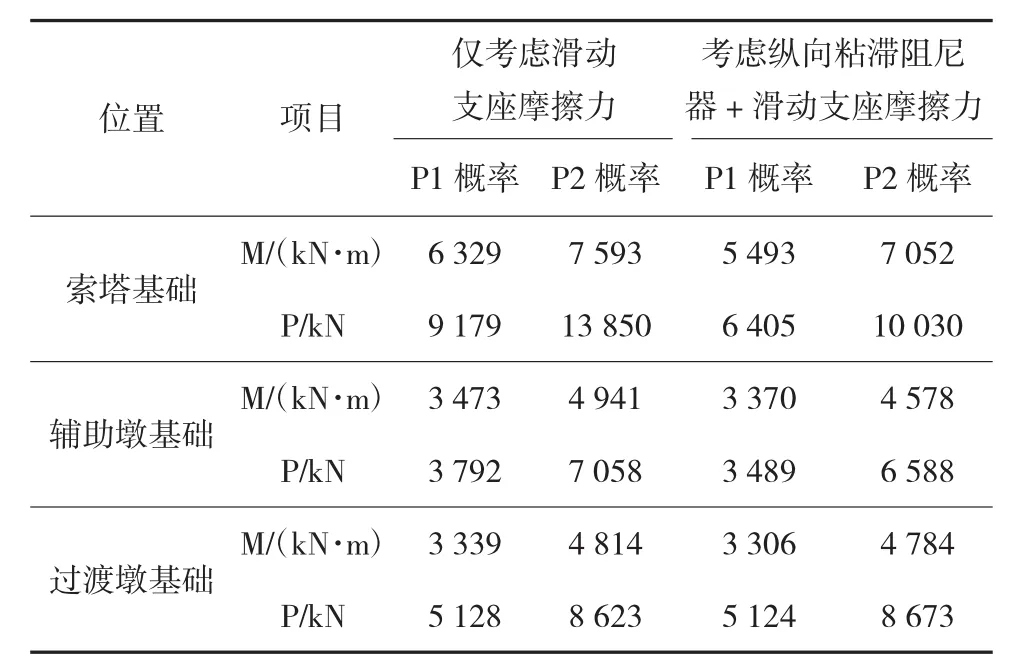
表4 最不利单桩顶内力

总体来看，安装粘滞阻尼器对索塔、主梁的振动起到较好的抑振作用，其一方面起到耗能阻尼作用，另一方面改变了索塔与主梁之间的能量传递体系，原主梁纵向振动约束力主要由拉索体系提供，并由拉索反向施加于索塔上塔柱锚固区，增设粘滞阻尼器后，由于阻尼力的作用，一方面使主梁水平振动能量发生衰减，降低了主梁水平位移峰值，另一方面阻尼力反作用至索塔下横梁处，改变了索塔承担的水平振动力的位置与大小，也显著改善了索塔塔柱及基础受力。

4 抗震设防水准及性能验算

桥梁抗震设计目标是减轻桥梁工程的地震破坏，减少经济损失，既要使震前用于抗震设防的经济投入不超过当前经济能力，又要使地震中经过抗震设计的桥梁破坏程度在可承受范围内。根据结构的重要性以及地震破坏后桥梁结构的修复（抢修）的难易程度，建议采用表5的设防标准进行抗震性能验算。

表5 本桥抗震设防标准

构件的初始屈服弯矩为截面最外层钢筋首次屈服（考虑相应轴力）时对应的弯矩，而等效屈服弯矩为根据截面M－φ分析（考虑相应轴力），把截面M－φ曲线等效为双线性所得到得等效屈服弯矩。桩基控制截面验算采用纤维单元，根据在恒载和地震作用下的轴力组合进行了M－φ分析，得出各控制截面的初始屈服弯矩及等效屈服弯矩，见表6，可作为检验桩基截面配筋的重要依据；经验算，与其他主要荷载组合工况相比，桩基截面配筋设计受地震荷载工况控制。

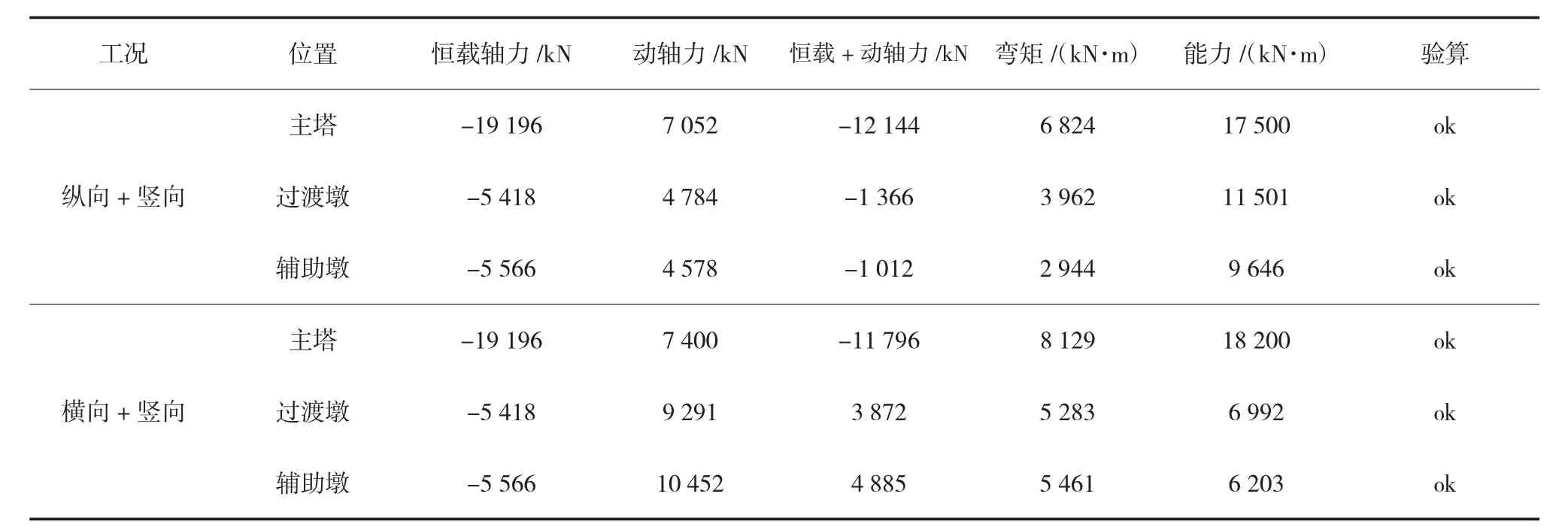
表6 主塔及过渡墩、辅助墩桩基截面验算（100 a 3%）

5 结论

（1）甬江特大桥作为全飘浮体系联塔分幅斜拉桥，具有固有频率比较低，模态分布比较密集的特点，尤其纵飘振型对桥梁的纵向地震反应起主要贡献。不同于常规桥塔，联塔分幅斜拉桥桥塔X连接（横梁）处截面也是受力控制截面，主要受双主梁反向纵飘振型产生的惯性力影响。

（2）塔梁间增设粘滞阻尼器连接后，塔顶及主梁纵向位移均大幅降低，但主梁竖向位移变化不大，该粘滞阻尼器耗能减震具有显著的方向性，即主要影响纵向变位，对其它方向基本无影响。

（3）塔梁间增设粘滞阻尼器连接后，索塔塔柱各关键截面及基础受力也有显著改善，说明粘滞阻尼器对索塔、主梁的振动均起到较好的抑振作用，但对远端的辅助墩及过渡墩及桩基影响较小。

（4）在常遇地震设防水准下，联塔分幅斜拉桥主要构件均在弹性范围内工作，在罕遇地震设防水准下，索塔、辅助墩及过渡墩柱及基础可以出现裂缝，但不影响使用。综合使全桥的抗震性能目标在经济与安全之间得到较好平衡。